Robust Quantum Computational Advantage Using Fermionic Linear Optics and Magic Input States

Michał Oszmaniec¹, ‪Zoltán Zimborás², Mauro Morales³,

Ninnat Dangniam¹

AQIS, 7-9 Dec 2020

¹ Center for Theoretical Physics, Polish Academy of Sciences, ² Wigner Research Centre for Physics, ³ Centre for Quantum Software and Information, University of Technology Sydney

  • Introduction and motivations
    • Quantum computational supremacy
    • Fermion Sampling with magic input states
    • Experimental prospects
  • Results: hardness guarantees and certification
    • ​Anticoncentration
    • Robust average-case hardness by Cayley path
    • Certification
  • Summary
  • Introduction and motivations
    • Quantum computational supremacy
    • Fermion Sampling with magic input states
    • Experimental prospects
  • Results: hardness guarantees and certification
    • ​Anticoncentration
    • Robust average-case hardness by Cayley path
    • Certification
  • Summary

Quantum computational supremacy

  • Quantum supremacy: the ability of a quantum system to perform a task that classical computers cannot, regardless of whether the task is useful 

 

  • Sampling problems can demonstrate quantum supremacy with few assumptions. Boson Sampling is the canonical example (Aaronson & Arkhipov, STOC'11)

 

  • Random circuit sampling (RCS) is the leading candidate due its rigorous hardness guarantees
    • One- and two-qubit gates are chosen randomly
    • Demonstrated on the 53-qubit Sycamore quantum processor (Arute et al., Nature 2019)

Movassagh 2019

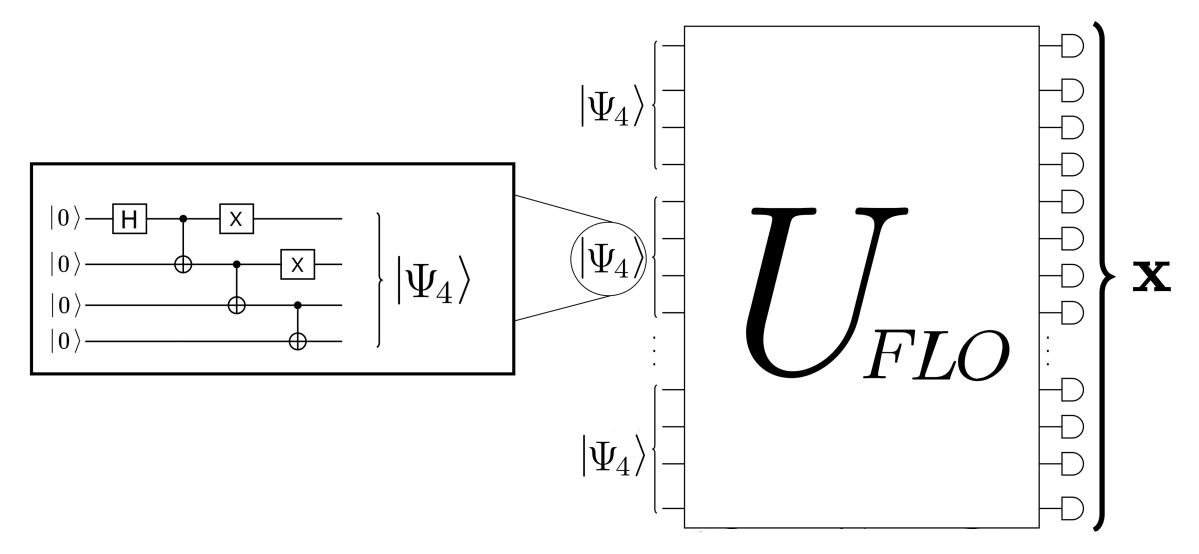
Fermion Sampling with Magic Inputs

  • Analogue of Boson Sampling: while fermionic linear optics (FLO) with fermion-number inputs are classically efficiently simulable, FLO supplemented with entangled "magic" states
|\Psi_{in}\rangle = |\Psi_4\rangle^{\otimes N} = \left( \frac{|0011\rangle + |1100\rangle}{\sqrt{2}} \right)^{\otimes N}

  • promotes (active) FLO to universal quantum computation (Bravyi & Kitaev, Ann Phys 2002, Bravyi, PRA 2006, Hebenstreit et al., 2020) 

  • leads to worst-case hard probabilities even when restricted to number-perserving (passive ) FLO (Ivanov, PRA 2017)

V_{FLO}

Experimental Prospects

FLO circuits (say under the Jordan-Wigner transformation) are native to superconducting qubit architecture

  • Two-qubit fermionic SWAP (iSWAP) gates realized with high fidelity in the demonstration of RCS on the 53-qubit Sycamore quantum processor (Arute et al., Nature 2019, Foxen et al., PRL 2020)
  • The same processor used for proof-of-principle quantum chemistry calculation (Arute et al., Science 2020), non-planar QAOA (Arute et al.  2020)

Google AI Blog

  • Introduction and motivations
    • Quantum computational supremacy
    • Fermion Sampling with magic input states
    • Experimental prospects
  • Results: hardness guarantees and certification
    • ​Anticoncentration
    • Robust average-case hardness by Cayley path
    • Certification
  • Summary

Groups of FLO transformations

\(d\) fermionic modes are described by \(d\) creation and \(d\) annihilation operators

\{f_j,f_k^\dagger\}\equiv f_j f_k^\dagger+ f_k^\dagger f_j = \delta_{j,k}

or \(2d\) majorana operators

m_{2j-1} = f_j^\dagger+f_j\, ,\qquad m_{2j} = i\, (f_j^\dagger-f_j),
  • Number-preserving (passive) FLO forms the group \(\mathrm{U}(d)\) of unitary matrices that do not mix creation and annihilation operators
  • Active FLO forms the group \(\mathrm{SO}(2d)\) are parity-preserving transformation
V_{act} = \exp\left( \frac{1}{4} \sum_{i,j=1}^{2d} \left[\log(O)\right]_{ij} m_i m_j\right),\qquad O \in \mathrm{SO}(2d)

Both groups are described by poly(\(d\)) parameters even though the groups act as circuits on Hilbert space \(\mathcal{H}\) of dimension exponential in \(d\)

Classical sampler

Result:

Anticoncentration

Approximations of \(p_{\mathbf x_0}(V,\Psi_{in})\)

on average

(over Haar distribution)

Result:

average-case hardness of approximating up to additive error \(\epsilon =\exp(-\Theta(N^6))\)

Our results supporting the supremacy conjecture

PH collapse

(conjectured to be false)

p_{\mathbf x_0}(V,\Psi_{in}) = |\langle{\mathbf x_0}|V|\Psi_{in}\rangle|^2

Conjecture: average-case hardness of approximating up to additive error \(\epsilon = (\dim\mathcal{H})^{-1}/poly(N)\)

Anticoncentration

\Pr_{V\sim \mathrm{Haar}} \left[ p_{\mathbf x_0}(V,\Psi_{in}) > \frac{\alpha}{|\mathcal{H}|} \right] > (1-\alpha)^2 C
  • We use the Paley-Zygmund inequality and moments calculated from the group-theoretic properties 
  • We do not use the 2-design property (In fact, \(\nu\) can be proven not to form a 2-design)
  • Numerics suggests that \(p_{\mathbf x_0}(V,\Psi)\) does not anticoncentrate if \(\Psi\) is Gaussian

For any \(0 < \alpha < 1\), There exists a constant \(C>0\) such that

Average-case hardness: Cayley path

(\mathcal{H})
  • Goal: construct a low-degree rational interpolation between a #P-hard FLO circuit and generic circuits
  • Use polynomial interpolation technique to recover the value of the worst-case probability from those of generic circuits 
  • To achieve the goal, we use the Cayley-path deformation (Movassagh 2019)

Difference to previous work: instead of deforming one- and two-qubit gates at the level of physical circuits, we deform at the level of the group element, which is then represented as a global circuit while maintaining the low-degree structure

\text{Passive and active FLO: }\ \ \deg = (O(N^2), O(N^2))
g_{\theta} = g_0\frac{(1-\theta) I +(1+\theta) g}{ (1+\theta) I +(1-\theta)g }

It is #P-hard to compute values of \(p_{\mathbf x_0}(V,\Psi_{in})\) with probability greater than \(\frac{3}{4}+\frac{1}{\mathrm{poly}{N}}\) over the choice of \(V\) w.r.t. the Haar measure

Average-case hardness

it is #P-hard to approximate probability \(p_{\mathbf x_0}(V,\Psi_{in})\) to within accuracy \(\epsilon =\exp(-\Theta(N^6))\) with probability greater than \(1-o(N^{-2})\) over the choice of \(V\) w.r.t. the Haar measure

Robustness

  • Movassagh's result: \(\epsilon =\exp(-\Theta(N^{4.5}))\) for the Google's layout
  • Supremacy conjecture: \(\epsilon = (\dim\mathcal{H})^{-1}/poly(N)\)

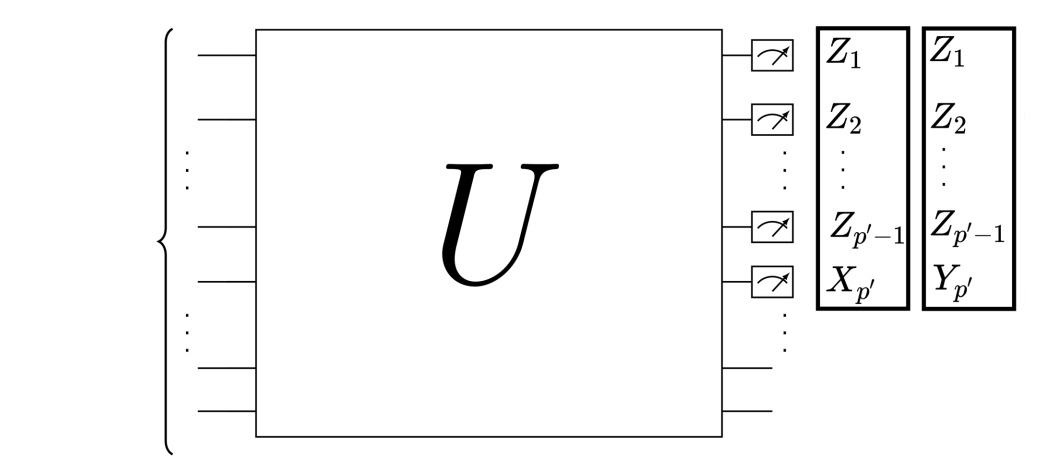
Certification

Assuming that the circuit is FLO, the circuit \(V\) can be efficiently estimated using \(poly(d,\epsilon^{-1})\) single-mode input states and computational-basis measurements, where \(\epsilon\) is the estimation error in the diamond distance

|+_X^p\rangle \\ \text{or} \\ |+_Y^p\rangle
|+_X^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_X\rangle \otimes |0\rangle^{\otimes (n-p)}, \qquad |+_Y^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_Y\rangle \otimes |0\rangle^{\otimes (n-p)}
p,p' = 1,2,\dots,d
V_{FLO}

Conclusion

  • We propose Fermion Sampling scheme with magic input states which utilize gate sets and architecture native to superconducting devices and has the potential to be realized in near-term
  • We provide state-of-the-art hardness guarantees by proving
    • Anticoncentration
    • Robust average-case hardness of computing the output probabilities
  • The hardness guarantees are comparable to RCS and surpassing Boson Sampling
  • Both results are derived using the group structure of FLO circuits
  • Assuming that we have an FLO circuit, the circuit can be certified efficiently using resources scaling polynomially with the system size