Optimal verification of stabilizer states

Ninnat Dangniam, Yun-guang Han, Huangjun Zhu

10 Aug 2020

Department of Physics and Center for Field Theory and Particle Physics, Fudan University

arXiv:2007.09713

Identitifying a quantum state

Trusted multi-qubit measurement

  • Quantum state tomography fully identifies an unknown quantum state
  • Sample-optimal tomography requires an exponential amount of resource (Haah et al., 2017), entangled measurements (serial or parallel)

i.i.d. quantum states

\(\sigma^{\otimes N}\) (possibly mixed)

\sigma

State space

Verifying a quantum state

Trusted single-qubit measurement

\(O_A \otimes I_B + I_A\otimes O_B \longrightarrow O_A \otimes O_B\)

classical post-processing

\epsilon
\rho

i.i.d. quantum states

\(\sigma^{\otimes N}\) (possibly mixed)

  • Quantum state verification aims to certify that \(\sigma\) is close to some target pure state \(\rho\) using only local projective measurements

State space

\langle\psi|\sigma|\psi\rangle \\ \le 1-\epsilon

\(XX\)

(relative

phase)

\(ZZ\)

(parity)

|\Phi^+\rangle = |00\rangle +|11\rangle
|\Psi^-\rangle = |01\rangle -|10\rangle
|\Phi^-\rangle = |00\rangle -|11\rangle
|\Psi^+\rangle = |01\rangle +|10\rangle
+1 +1
-1 +1
+1 -1
-1 -1

For general pure states (linear combinations of the four Bell states) and mixed states, there will be a failure probability to detect the target state 

 

Example: Distinguishing Bell states

(\(|\Phi^+\rangle\langle\Phi^+|\) is nonlocal)

Measure \(\{\Pi_j, I-\Pi_j\}\) with probability \(p_j\)

Obtain

\(\Pi_j\)

Obtain

\(I-\Pi_j\)

Reject

The hypothesis testing scenario

\delta\approx e^{-N\nu\epsilon}

Chernoff-Stein lemma

\(\sigma=\rho\): Accept with probability 1

(No type I error)

\(\epsilon\)-far: Accept with probability \(\delta\) (type II error)

\Omega|\psi\rangle := \left(\sum_j p_j \Pi_j\right)|\psi\rangle = |\psi\rangle

\(|\psi\rangle\) is a +1 eigenstate of the verification operator

N = \left\lceil \displaystyle{\frac{\ln\delta^{-1}}{\nu(\Omega)\epsilon}} \right\rceil

spectral gap \(\nu(\Omega)\)

Pallister et al., PRL 120 170502 (2018)

Zhu & Hayashi, PR Appl. 12, 054047 (2019)

Test projector

Existing results

Efficient? Optimal?
Bipartite pure states
GHZ
Hypergraphs          *
(Phased) Dicke states
Antisymmetric basis states
Stabilizer states ?

Pallister et al., PRL 120 170502 (2018)

Our work

Main results for this talk

  • There is an efficiency bound for verification of stabilizer states that does not depend on the number of qubits or the specific stabilizer states
  • The bound can be saturated, at least up to seven qubits, by explicitly constructing an optimal measurement scheme

Stabilizer and graph states

Stabilizer states

Efficiently describable states

Cluster states

  • Resource states for MBQC

GHZ state

  • Quantum error correction
  • Secret sharing
G=(V,E)
S_j = \bigotimes_{(j,k)\in E} Z_k \otimes X_j
  • Every stabilizer state is LU-equivalent to some graph state
  • Stabilizer state = stabilized by a commuting subgroup of the \(n\)-qubit Pauli group

\(\mathcal{P}_n = \{\pm 1,\pm i\}\cdot\{I,X,Y,Z \}^{\otimes n}\)

       that does not contain \(-I\), called a stabilizer group \(\mathcal{S}\)

  • Completely speficified by \(n\) independent generators of the group

Graph states

X
Z
Z

Every convex combination of stabilizers in \(\mathcal{S}\) of a target stabilizer state \(|\psi\rangle\) has \(|\psi\rangle\) as a +1 eigenstate, but not all of them are measurable locally

Characterizing test projectors

\Omega:= \sum_j p_j \Pi_j
\Pi_{\mathcal{L}_P} = \frac{1}{|\mathcal{L}_P|} \sum_{\mathcal{L}_P} s = \prod_{\langle\{s_k\}\rangle = {\mathcal{L}_P}} \displaystyle{\frac{1+s_k}{2}}

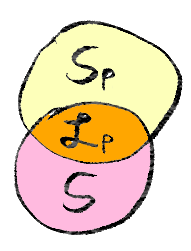
\(\mathcal{S}_P\) = stabilizer group generated by all single-qubit Pauli operators that constitute a Pauli measurement

\mathcal{L}_P = \mathcal{S} \cap \mathcal{S}_P

Local subgroup

Example: GHZ state

XXXX...
ZZI...
IZZI...
IIZZI...

Measuring ZZ... effectly measures half of the stabilizer group

Canonical test projector

|000\cdots\rangle\langle000\cdots|+|111\cdots\rangle\langle111\cdots|

Verification of stabilizer states

Unique optimal strategy if restricted to stabilizer measurements: measuring all stabilizers with equal probabilities 

\nu(\Omega) = \displaystyle{\frac{2^{n-1}}{2^n-1} }\overset{n\to\infty}{\longrightarrow}\displaystyle{\frac{1}{2}}

More general measurements?

Pallister, Linden and Montanaro, PRL 120 170502 (2018)

Wang and Hayashi, arXiv:1901.09467 [quant-ph]

(2/3 when \(n=2\))

  • Increasing the dimension of one half of a maximally entangled bipartite system cannot increase \(\nu(\Omega) = 2/3\) 
  • But every stabilizer state is maximally entangled w.r.t. any \((\mathcal{C}^2, (\mathcal{C}^2)^{\otimes n})\)-bipartition

Spectral gap is upper bounded by 2/3

  • Increasing the dimension of one half of a maximally entangled bipartite system cannot increase \(\nu(\Omega) = 2/3\) 
  • But every stabilizer state is maximally entangled w.r.t. any \((\mathcal{C}^2, (\mathcal{C}^2)^{\otimes n})\)-bipartition

Spectral gap is upper bounded by 2/3

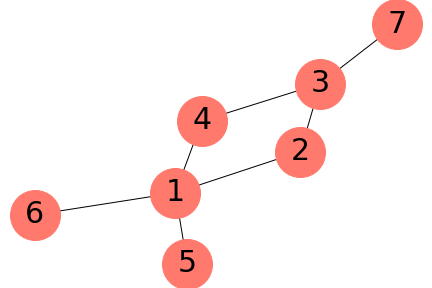
The algorithm

The bound can be saturated for all graph states up to seven qubits by explicitly constructing the optimal measurement scheme

  • All computation is done in the symplectic vector formalism
s(u)s(v) = i^{2[u,v]} s(v)s(u)
A_u = (M_{\mathcal{S}_u})^T J M_{\mathcal{S}}
J = \begin{pmatrix} 0 & -I_n \\ I_n & 0 \end{pmatrix}

 

  • Construct the local stabilizer projector.
  • Optimize the spectral gap (\(l_{\infty}\)-norm minimization - a linear program hence efficient)
  • Do this for all 45 LU-equivalent classes of graph states (LC-equivalent to stabilizer states)

Hein, Eisert and Briegel, PRL 69 062311 (2004)

Paulis Probabilities
ZXZXXXX
ZZYYXXZ
ZYXZXXY
XZZYZYX
XZXZZZZ
XXXXYZY
XYYYYYY
YZYZZYY
YXYXZZZ
YYZZYYX
YYXYYZZ		 1/6
1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
​1/12

The algorithm

Other results

  • Necessary condition for optimal verification by Pauli measurements \(p_x=p_y=p_z=1/3\)
  • Optimal XZ strategies (\(\nu = 1/2\)), optimal strategy for odd ring states (simplest non 2-colorable graph)
  • Admissible test projector = canonical test projectors that do not contain any other test projector, admissibility of XZ measurements \(\iff\) maximal independent set
  • Minimal number of settings for verification
\tilde{\chi}(G) \le \tilde{\chi}_2(G) \le \chi_{\mathrm{LC}}(G) \le \chi(G)

Equality for all graph states up to seven qubits