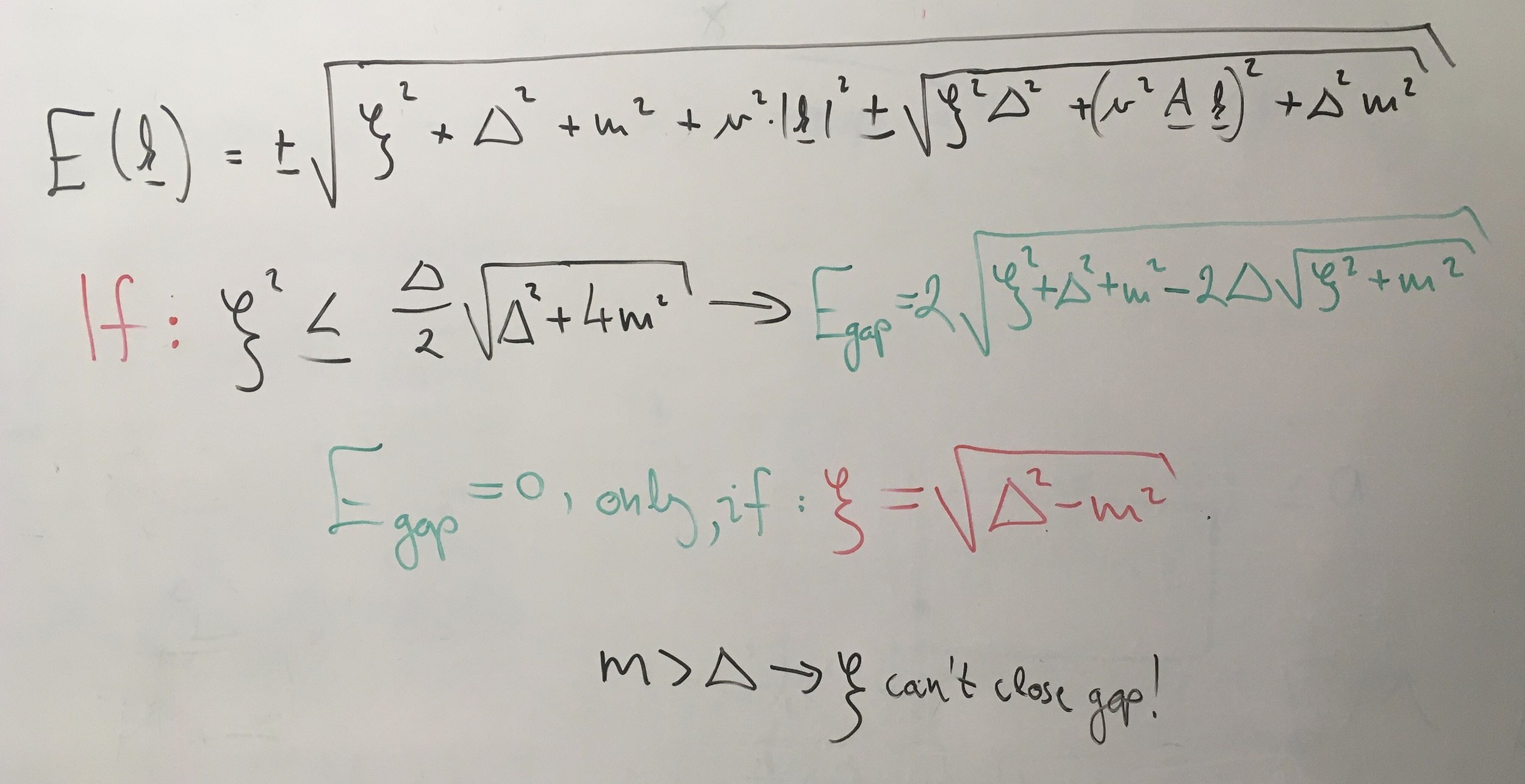Competition of trivial and topological phases in graphene based hybrid systems
Zoltán Tajkov
PhD Student
CMD2020GEFES, 2 September 2020



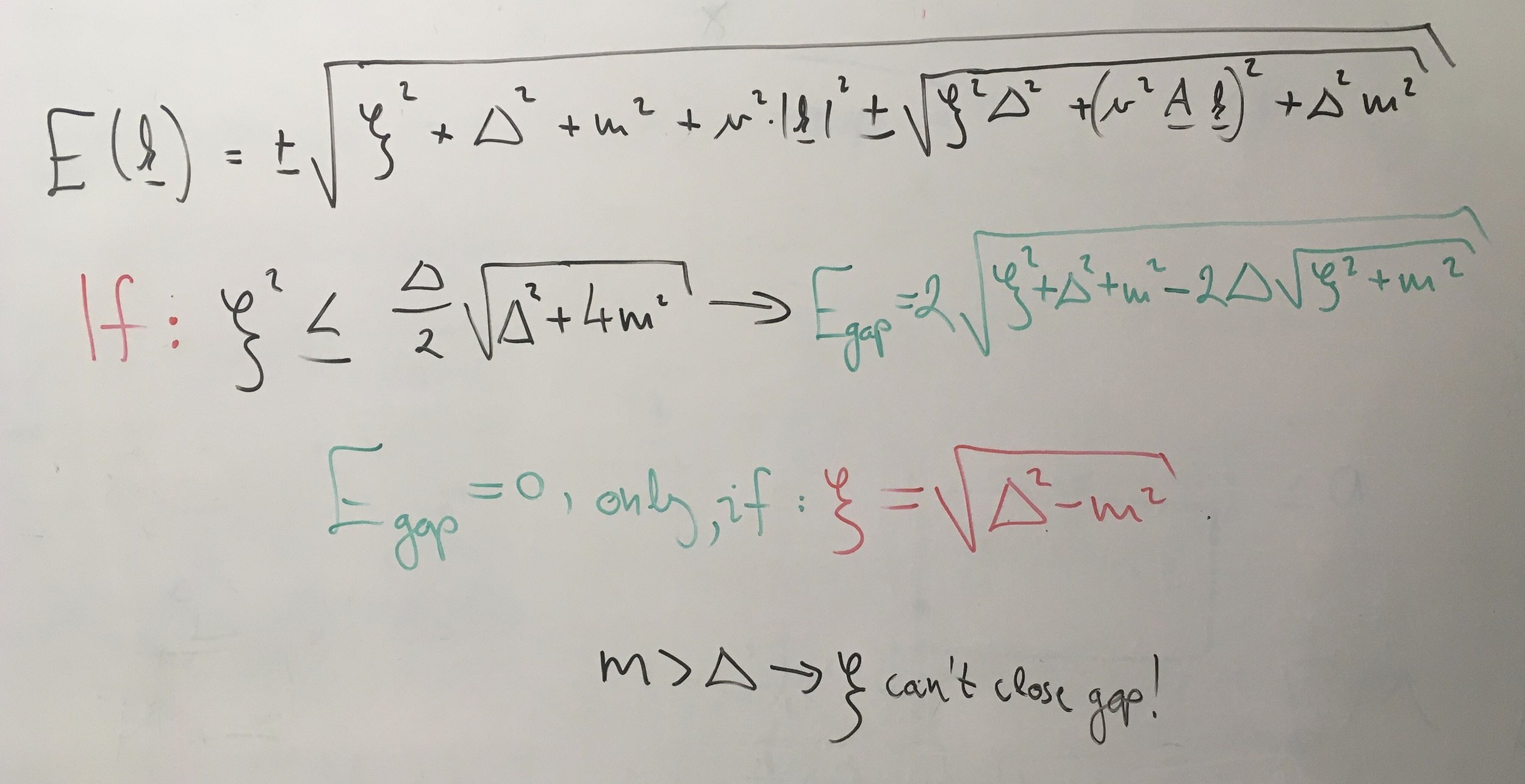

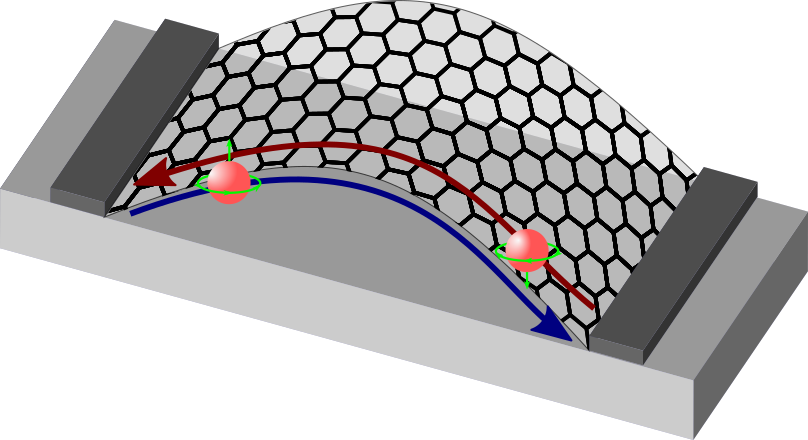
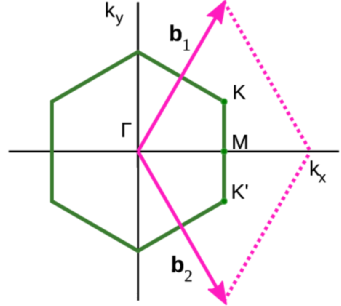
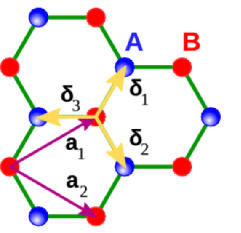
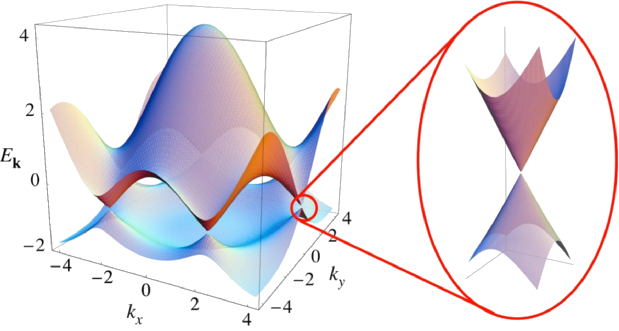
Graphene is ...
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)



Graphene is ...
... a good template!
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
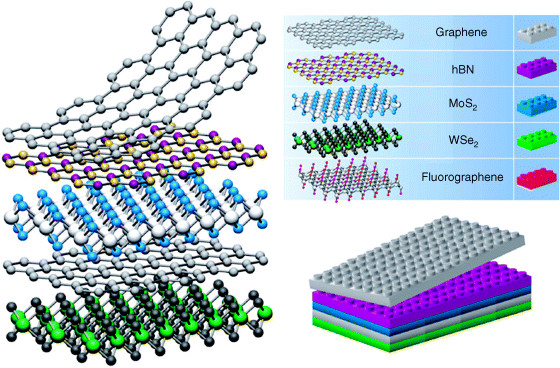



Graphene is ...
... a good template!
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)

How can we induce topological phase into graphene?



Graphene is ...
... a good template!
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)

How can we induce topological phase into graphene?

SOC!!

BiTeX: giant SOC
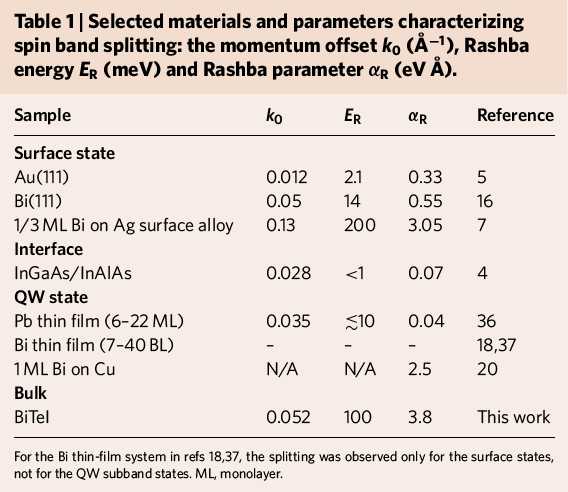
Ishizaka et al. Nature Materials 10, 521 (2011)
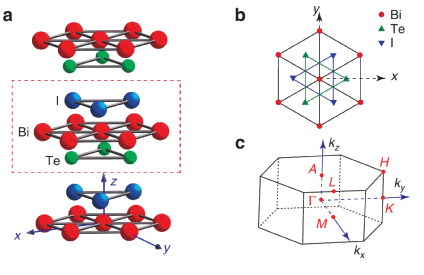
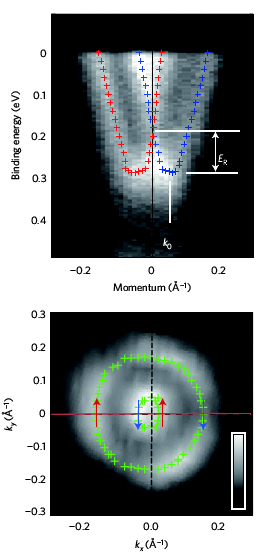
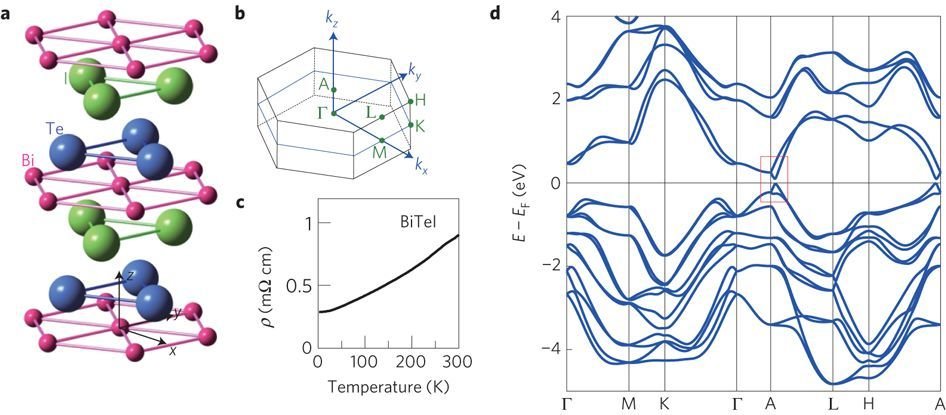
BiTeX monolayer
Fülöp et al. 2D Mater. 5, 031013 (2018)

BiTeX/graphene heterostructures
Geometry
Z. Tajkov et al. Nanoscale 11, 12704 (2019)


BiTeX/graphene heterostructures
DFT results for tellurium faced arrangements
Z. Tajkov et al. Nanoscale 11, 12704 (2019)



Z. Tajkov et al. Nanoscale 11, 12704 (2019)
Tiny, trivial gap
What can we do about it?
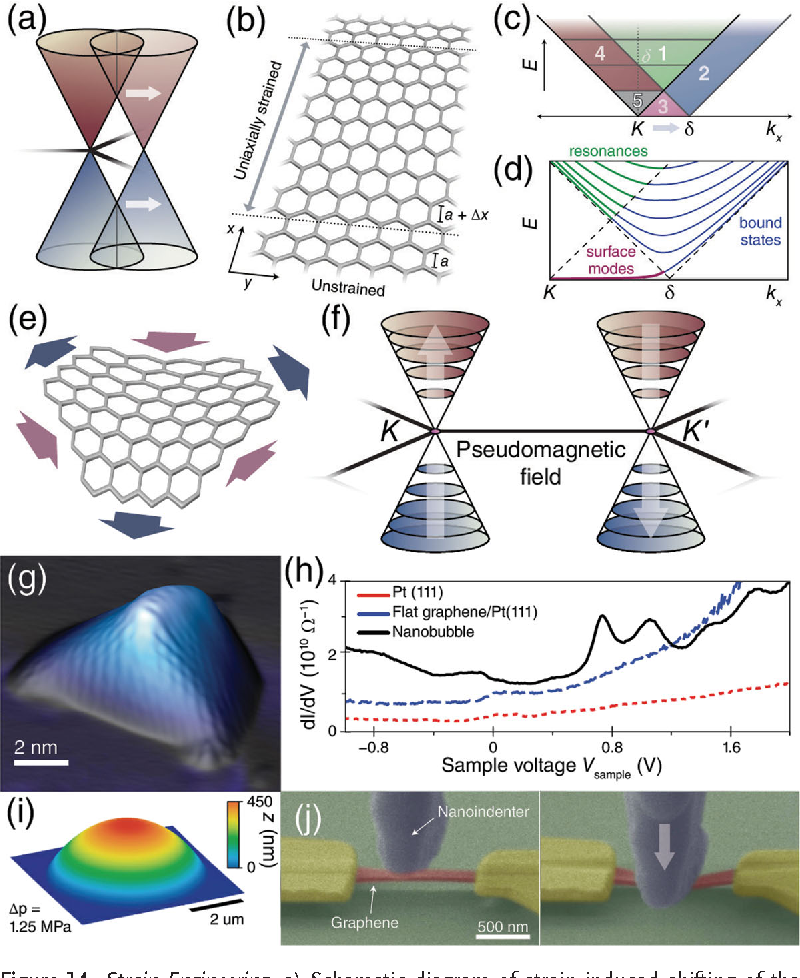



Mechanical distortions
in graphene
Weiss et al. Advanced Materials, 24 5782(2012)
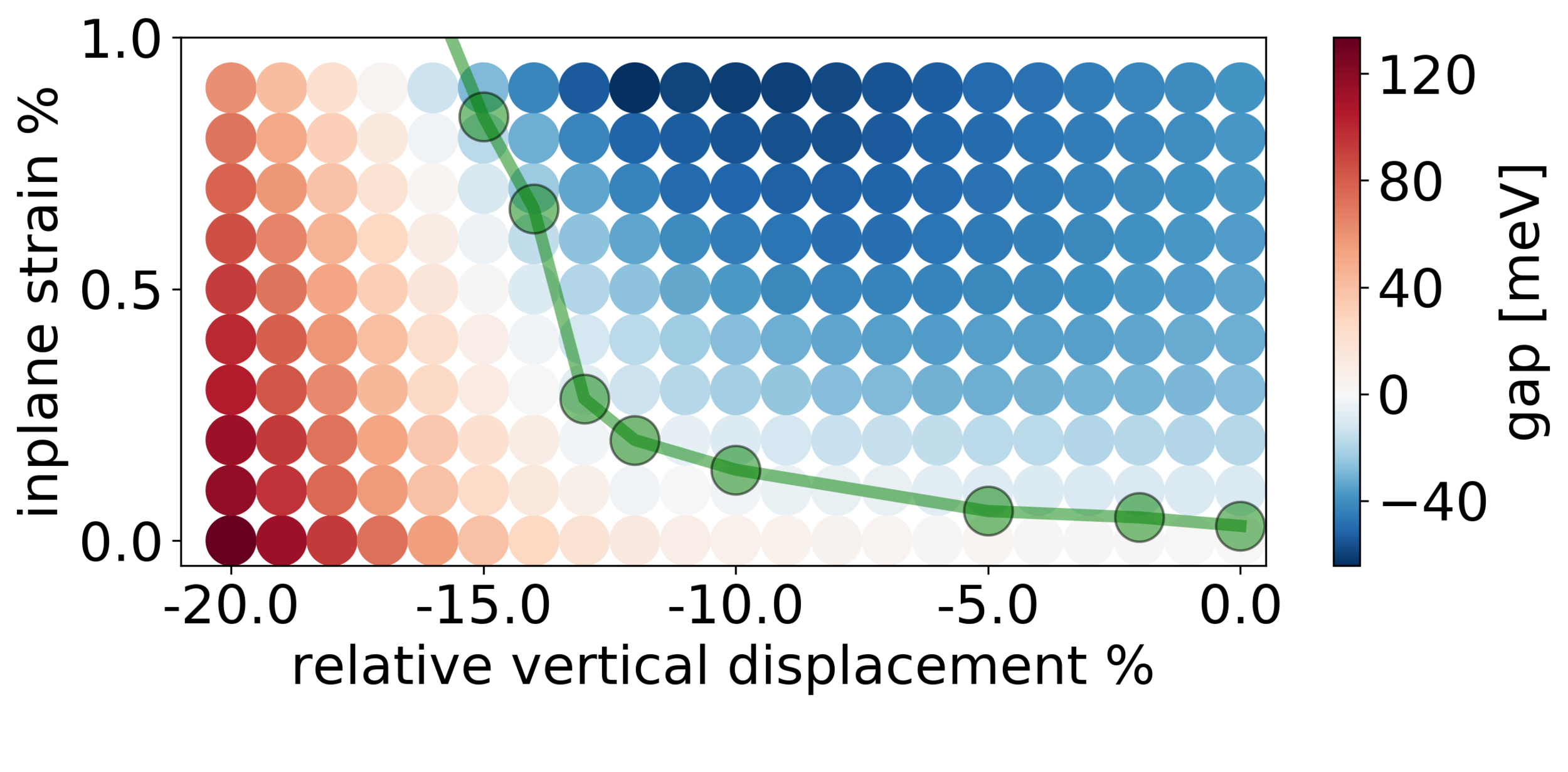
Pressure→I, inplane strain →TI !?!
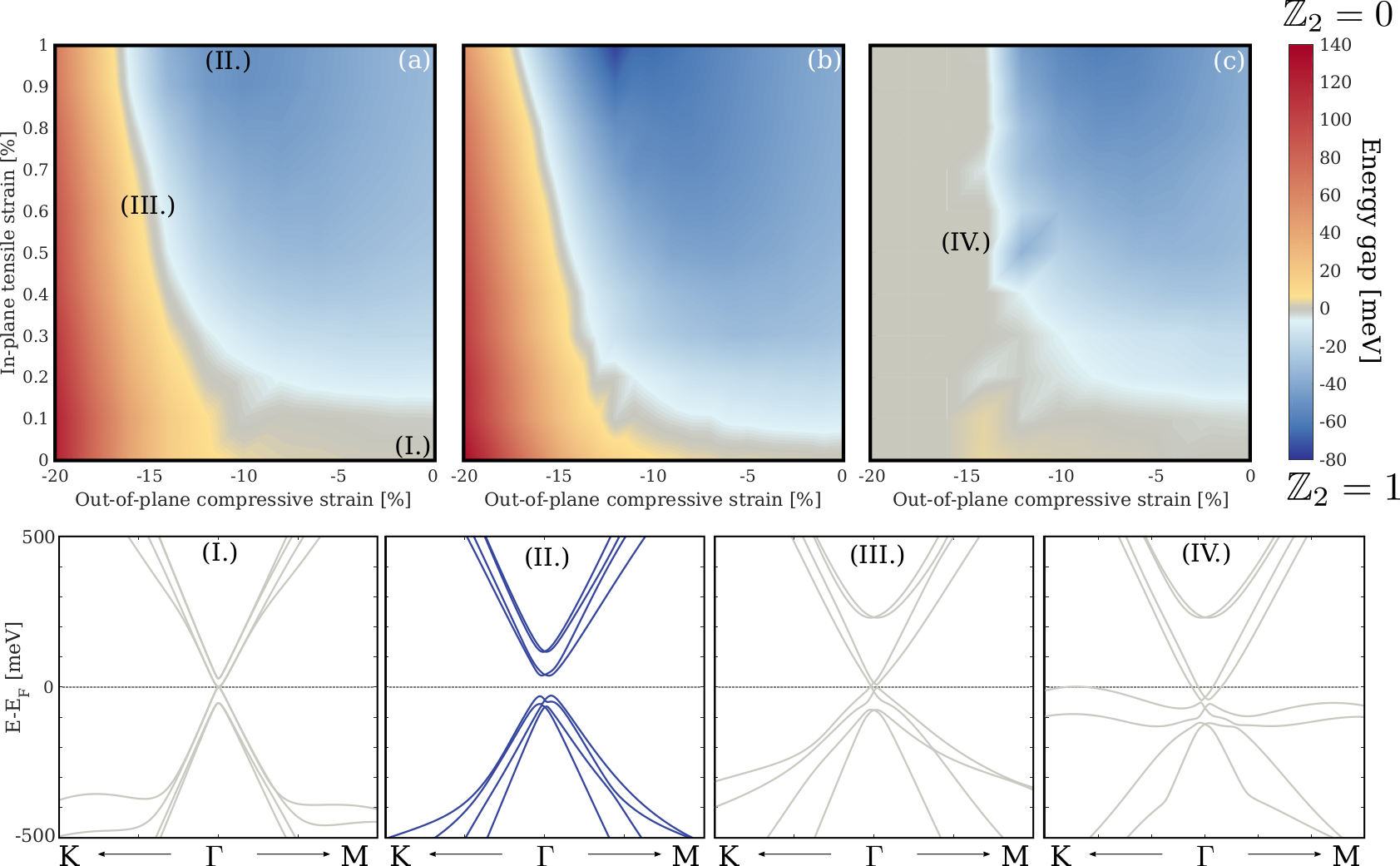
Z. Tajkov et al. Appl. Sci. 9, 4330 (2019)
BiTeBr
BiTeCl
BiTeI

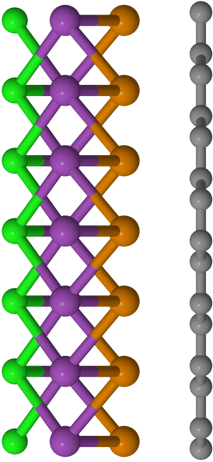
pressure
strain
What did we learn from DFT?
The most important parameters


Kekulé
Kane-Mele

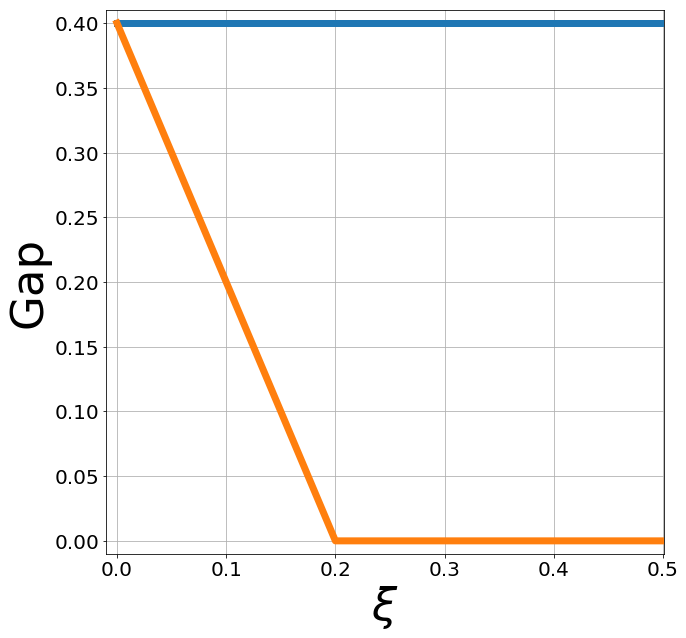
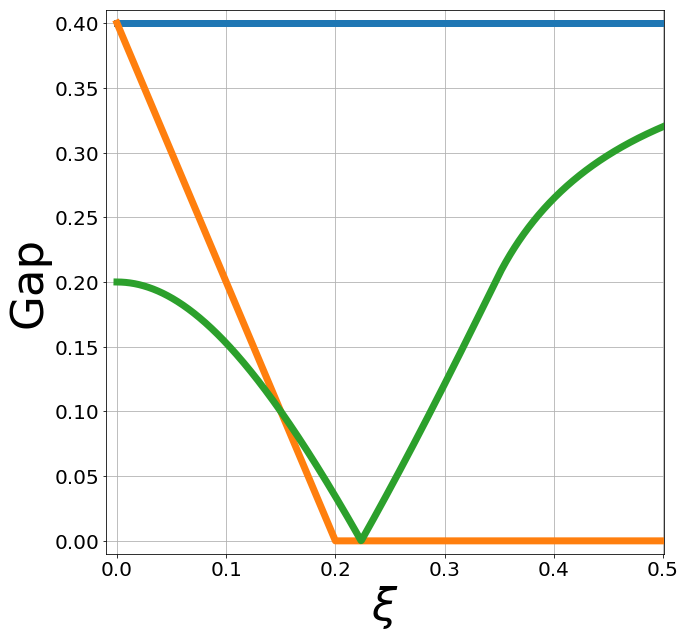
Strain promotes SOC \( \rightarrow \) TI
Strain can close the gap at \(\boldsymbol{k}=\boldsymbol{0}\) if
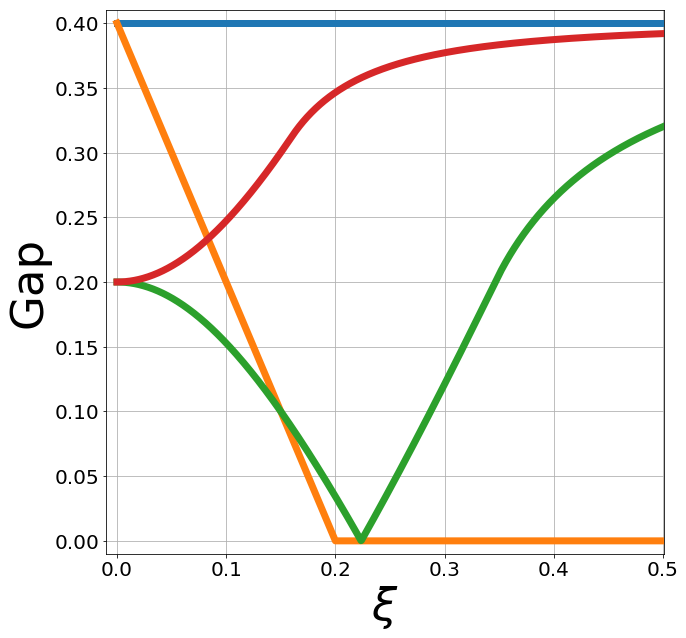
Minimal model
Z. Tajkov et al. Phys. Rev. B 101, 235146 (2020)
Strain kills Kekulé but KM gap is resilient!

The Team


László Oroszlány
János Koltai
József Cserti

Thank You!


László Oroszlány
János Koltai
József Cserti

Z. Tajkov et al. Nanoscale 11, 12704 (2019)
Z. Tajkov et al. Appl. Sci. 9, 4330 (2019)
Z. Tajkov et al. Phys. Rev. B 101, 235146 (2020)