Proximity-Induced Magnetic Phases in CrI3 Monolayers Coupled to WSe2

Eötvös Loránd University
Centre For Energy Research

Zoltán Tajkov








The Team



- László Oroszlány, Zoltán Tajkov, János Koltai, Dániel Pozsár, Andor Kormányos, András Balogh, Tamás Véber, Marcell Sipos
- Jaime Ferrer, Amador Garcia Fuente, Gabriel Martinez-Carracedo, Aurelio Hierro Rodriguez, Balázs Nagyfalusi, Rosa Eulalia González Ferreras
- Felix Büttner, Kai Litzius, Steffen Wittrock
- Efren Navarro-Moratalla, Marta Galbiati, Jose Joaquin Perez Grau
- László Szunyogh, László Udvardi, Bendegúz Nyári, Anjali Jyothi Bhasu



























Heisenberg model and DFT perturbation theory

DFT through
RKKR
&
Liechtenstein, Katsnelson , Antropov, Gubanov
J. Magn. Magn. Mater. 67 65 (1987)
Oroszlány, Ferrer, Deák, Udvardi, Szunyogh
Phys. Rev. B 99, 224412 (2019)
What is \(\delta \hat{V}_i\) ?
3) The definition of local operator in a non-orthogonal basis needs a pragmatic choice!
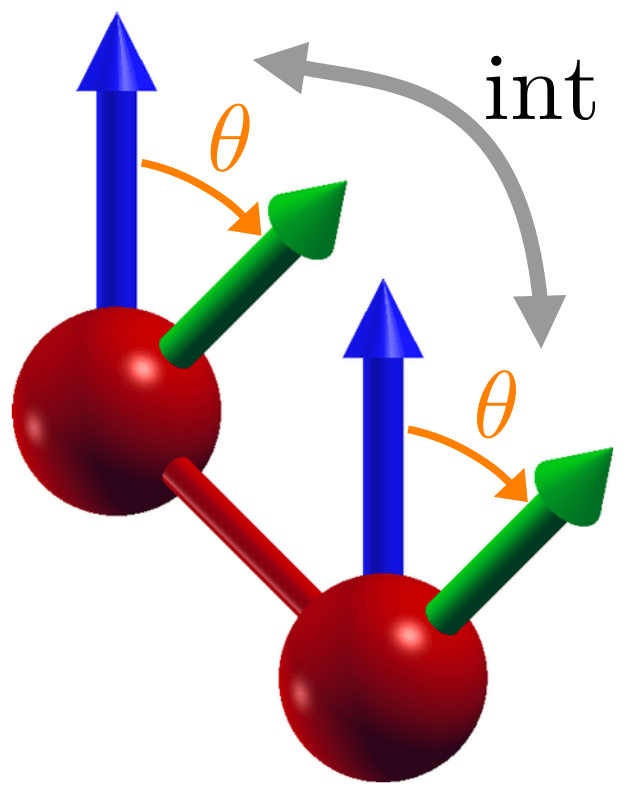
1) We need to rotate the magnetic moment!
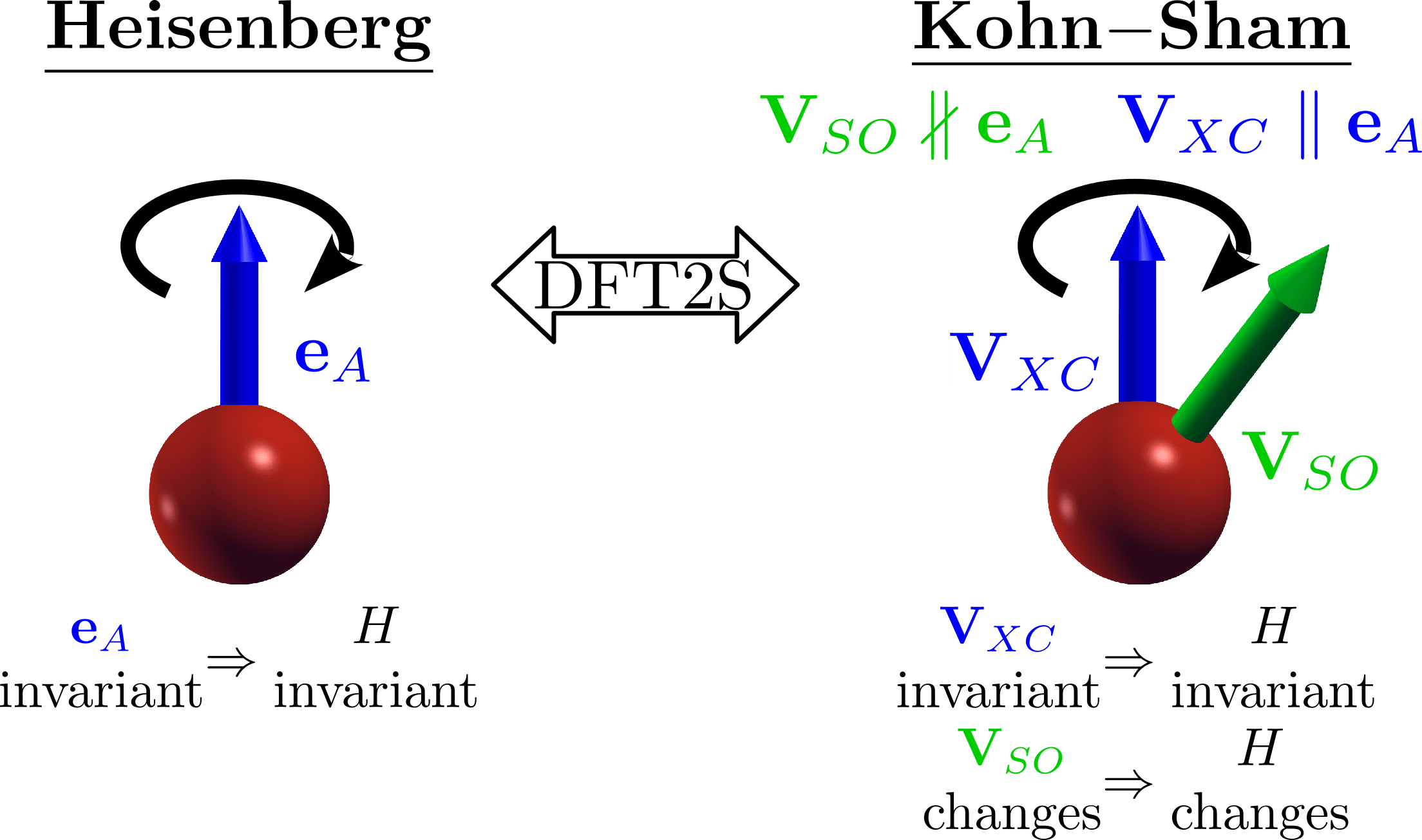
2) We need to identify the magnetic entity!
Could be:
- Single atom
- Cluster of atoms
- Certain orbitals inside an atom
Relativistic magnetic model parameters
Udvardi, Szunyogh, Palotás, Weinberger
Phys. Rev. B 68, 104436 (2003)
Martínez-Carracedo, Oroszlány, García-Fuente, Nyári, Udvardi, Szunyogh, Ferrer
Phys. Rev. B 108, 214418 (2023)
Istropic
exchange
Symmetric traceless exchange
Dzyaloshinskii - Moriya vector
On-site
anisotropy

Grogu
State of GROGU
Udvardi, Szunyogh, Palotás, Weinberger
Phys. Rev. B 68, 104436 (2003)
Martínez-Carracedo, Oroszlány, García-Fuente, Nyári, Udvardi, Szunyogh, Ferrer
Phys. Rev. B 108, 214418 (2023)

Grogu
- Full SIESTA support
- GPU support
- Relativstic parameters
- Flexible API to set up more complicated systems with complex magnetic entities
- Command line interface to extract and visualize the magnetic parameters
- Multiple output formats for atomistic spin dynamics softwares
Coming soon:
- Wannier90 support
- OpenMX support
- Higher order interaction

Showcase: CrI3 monolayer
Cr
I
- Semiconductor
- Experimental \( T_C \) is around 45 K
- Superexchange


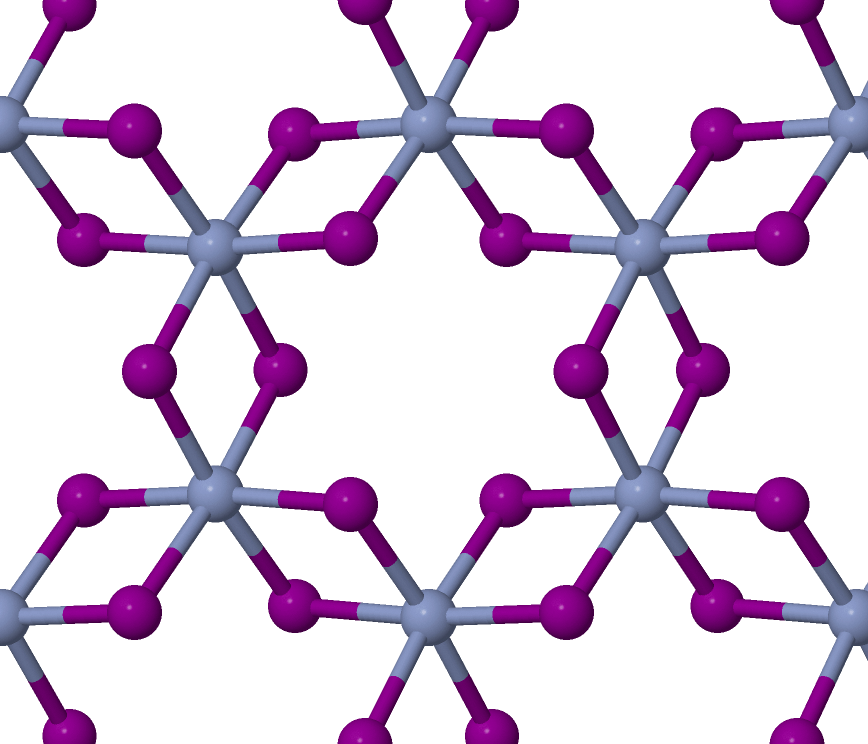
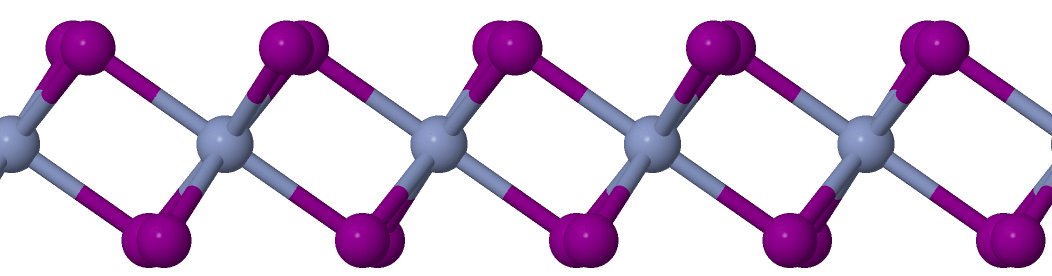
Showcase: CrI3 monolayer


d=1.59 \( \AA \)
Unit cell length: 7.06 \( \AA \)
Exchange parameters [meV]:
-0.4
-1.0
0.2
0.0
0.14
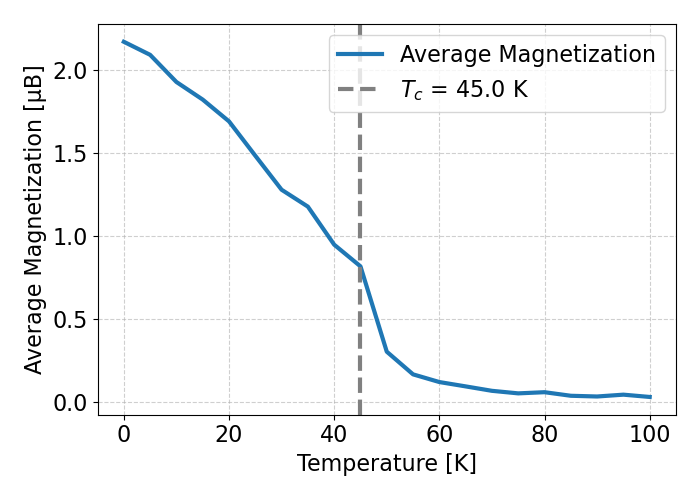
Calculated \( T_C \) is around 45 K
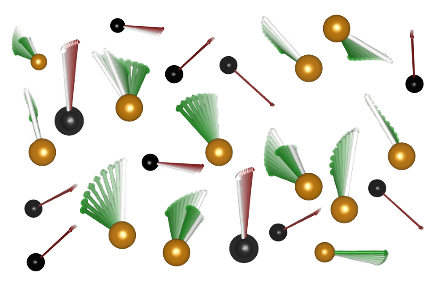
Uppsala Atomistic Spin Dynamics software


0.47

Showcase: CrI3 monolayer + WSe2


NO WSe2
Exchange parameters [meV]:
-0.4
1.7
-1.0
-1.4
0.5
0.0
0.16
0.14
0.21
0.47
0.61
Cr
I
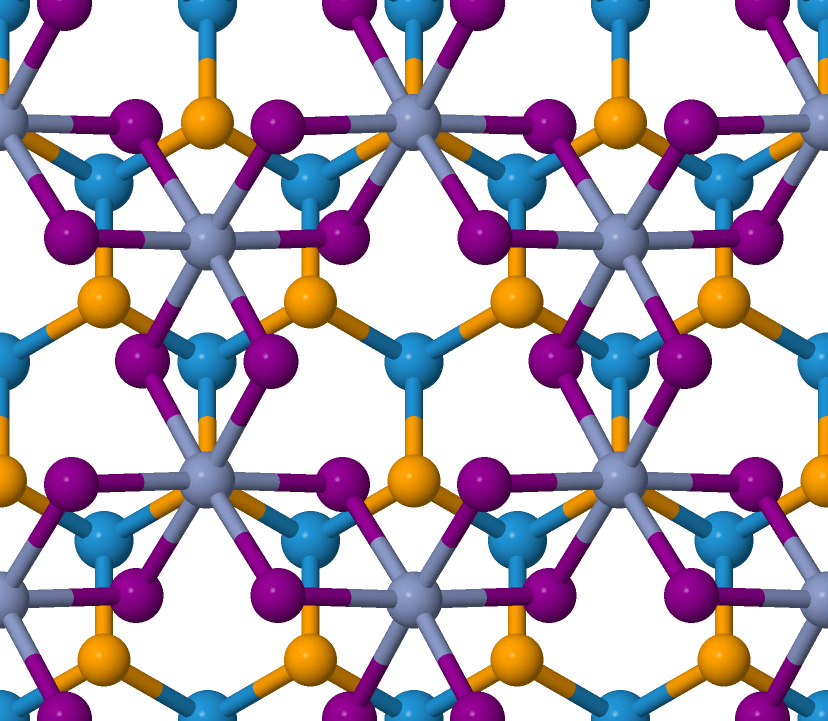
W
Se
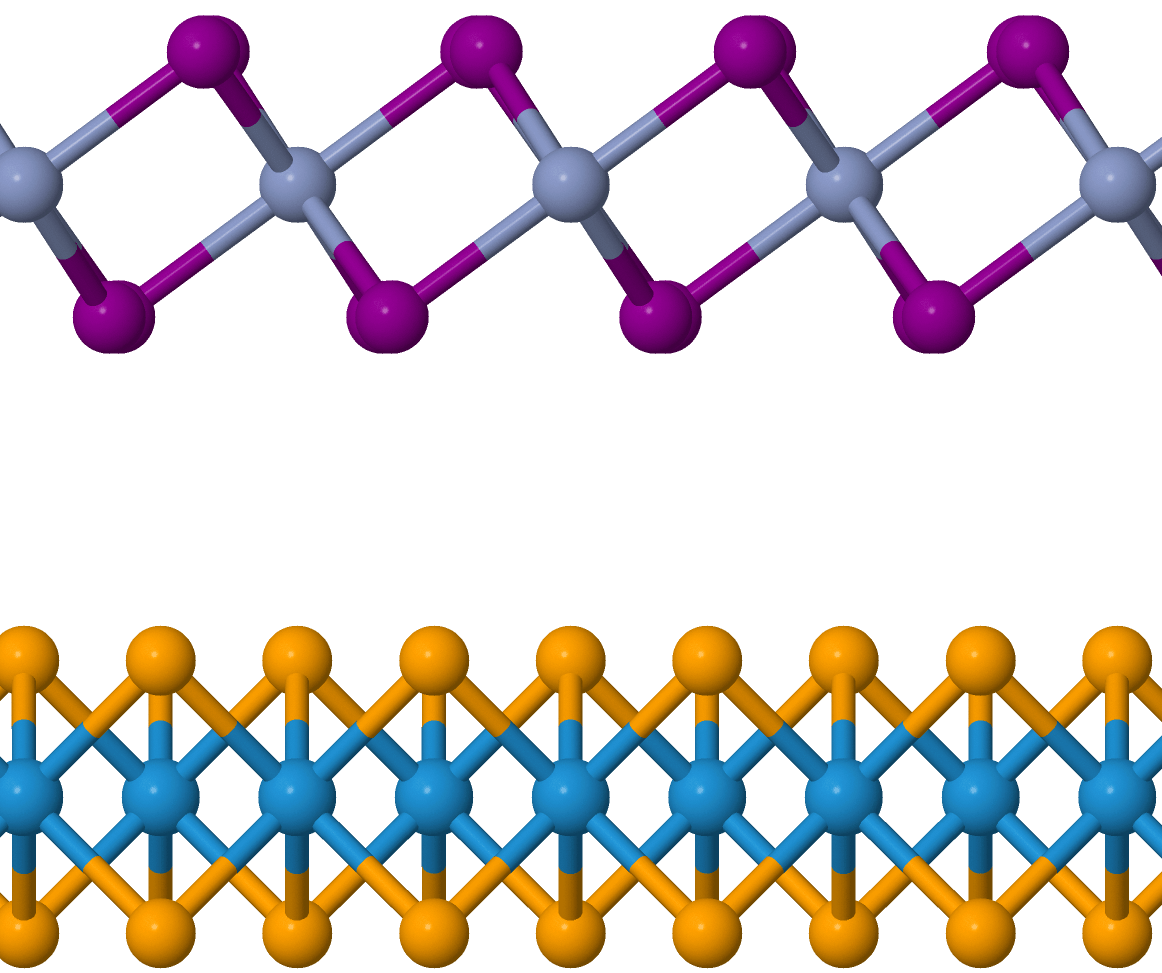
d \( = 1.64 \AA \)
Unit cell length: 6.74 \( \AA \)
d\(_\mathrm{vdW} = 4.23 \AA\)
YES WSe2
Large, 5% strain
0.2
Showcase: CrI3 monolayer + WSe2


NO WSe2
Exchange parameters [meV]:
-0.4
1.7
1.9
-1.0
-1.4
-1.5
0.5
0.6
0.0
0.16
0.14
0.14
0.21
0.22
0.47
0.61
N.A.

Unit cell length: 6.74 \( \AA \)
YES WSe2
Large, 5% strain
0.2
NO WSe2
-5% strain

missing
We need better twist angle!
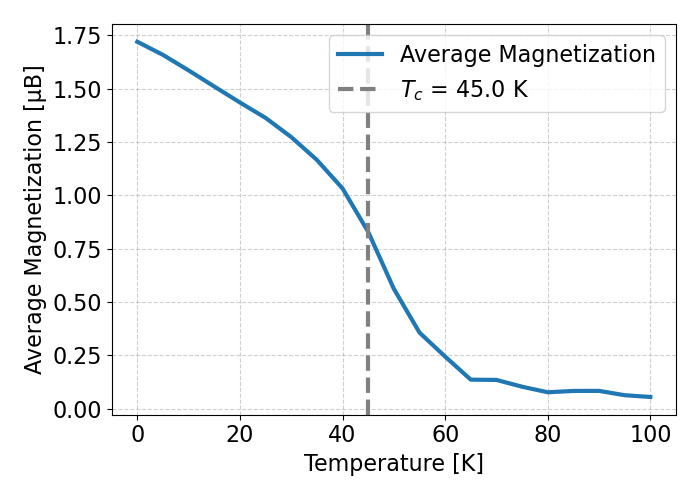
Very similar \( T_c \)

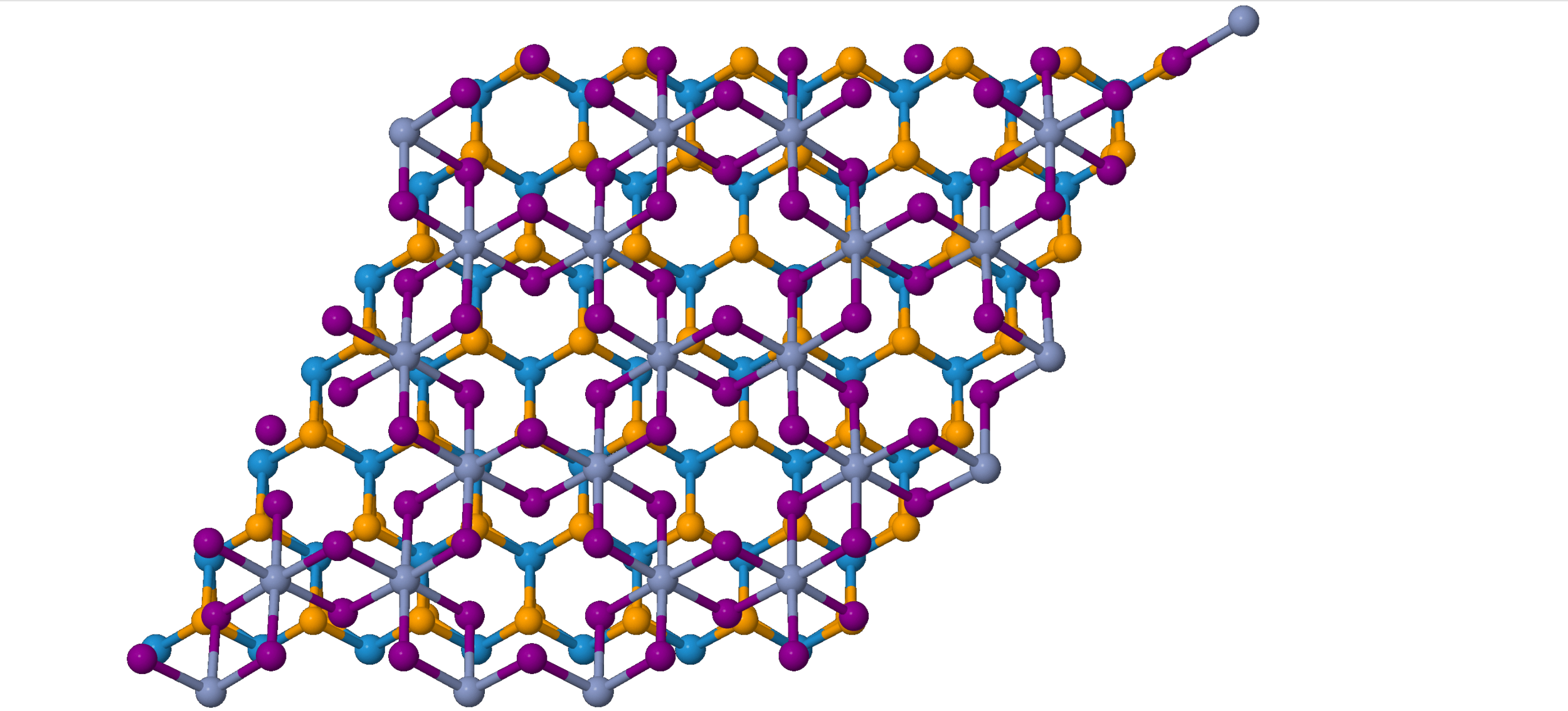
Showcase: CrI3 monolayer + WSe2


Exchange parameters [meV]:

NO WSe2
YES WSe2
NO WSe2 , -5% strain

-0.4
1.7
1.9
-1.0
-1.4
-1.5
0.5
0.6
0.0
0.16
0.14
0.14
0.21
0.22
0.47
0.61
N.A.
0.2

The servers are down...

Showcase: CrI3 monolayer + WSe2


Exchange parameters [meV]:

NO WSe2
YES WSe2
NO WSe2 , -5% strain

-0.4
1.7
1.9
-1.0
-1.4
-1.5
0.5
0.6
0.0
0.16
0.14
0.14
0.21
0.22
0.47
0.61
N.A.
0.2


Preliminary results!
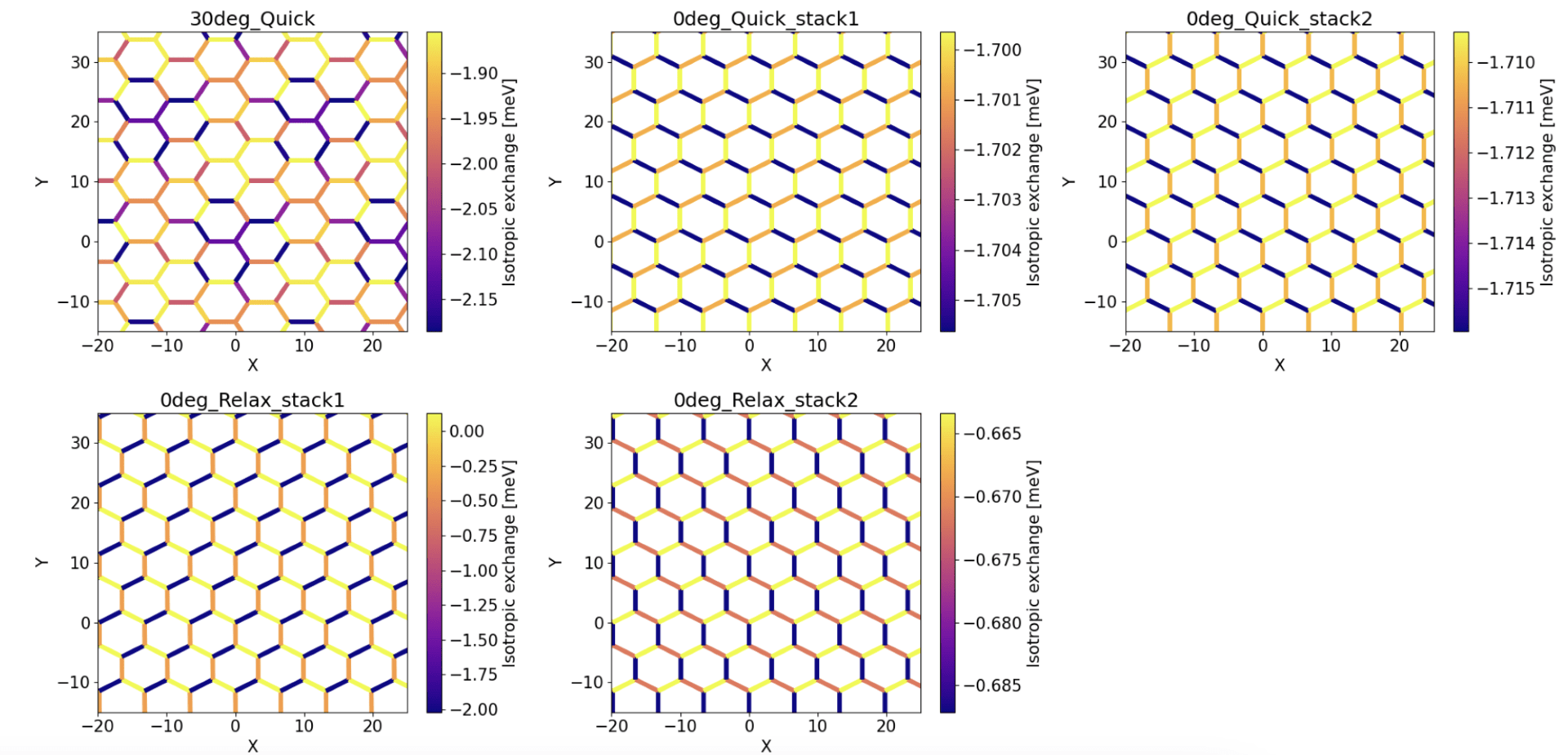
GROGU is a post processing tool
The results are as good as your DFT
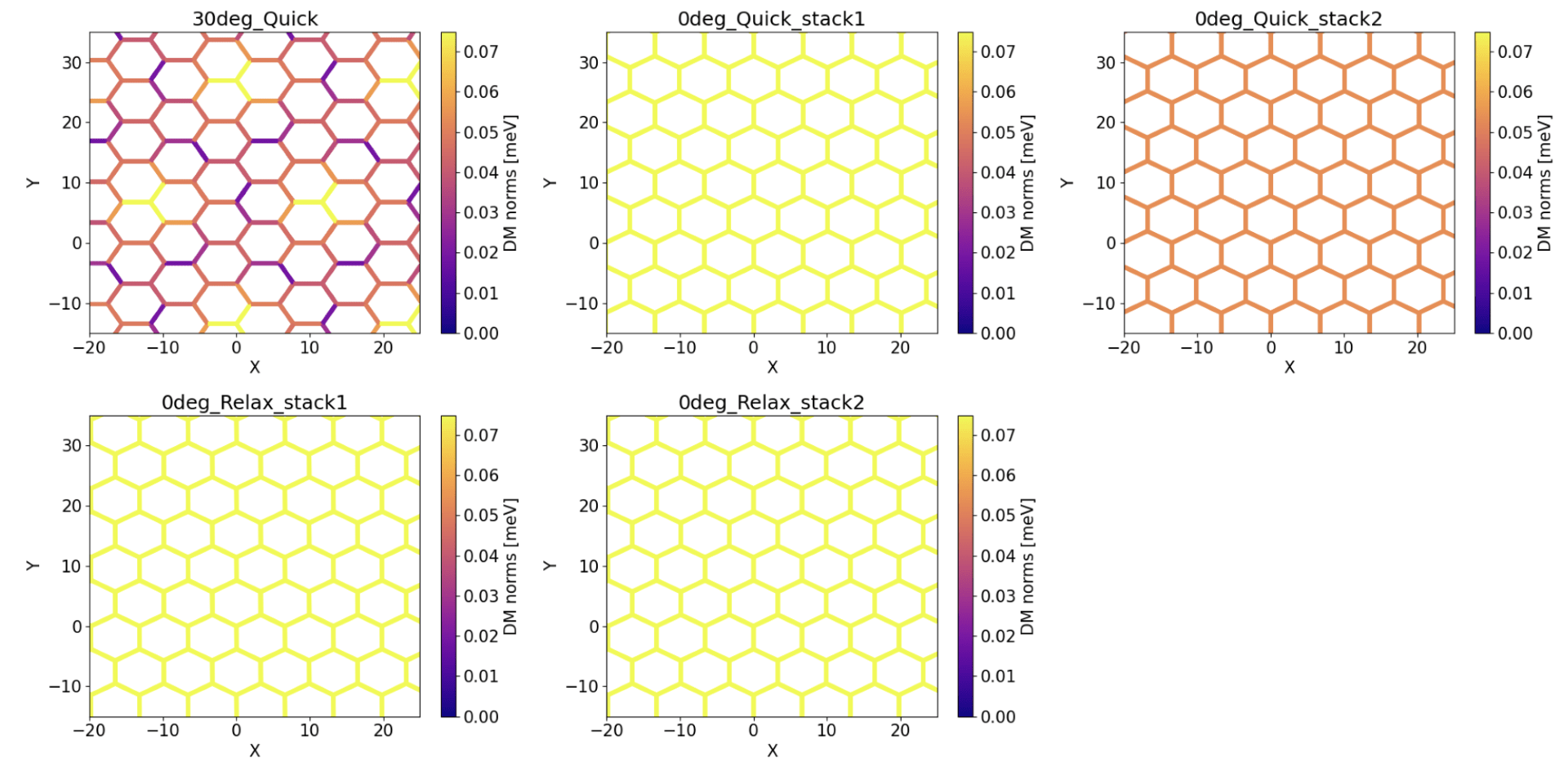


Relativistic magnetic interactions
- Very early release !!
- https://github.com/danielpozsar/grogu
- Single DFT calculation
- Pair creation is extremely cheap
- parallel BZ integral with MPI or CUDA
- Generalised Heisenberg model

UNDER 1 Hour on 8 GPUs
