Revealing the topological phase diagrams of 2D heterostructures using SIESTA
ELTE
Zoltán Tajkov
Kick-off meeting 2024.09.26


outline
siesta
Powerful DFT tool utilizing localized basis set. This means it provides a tight-binding Hamiltonian. Also models open-boundary systems.

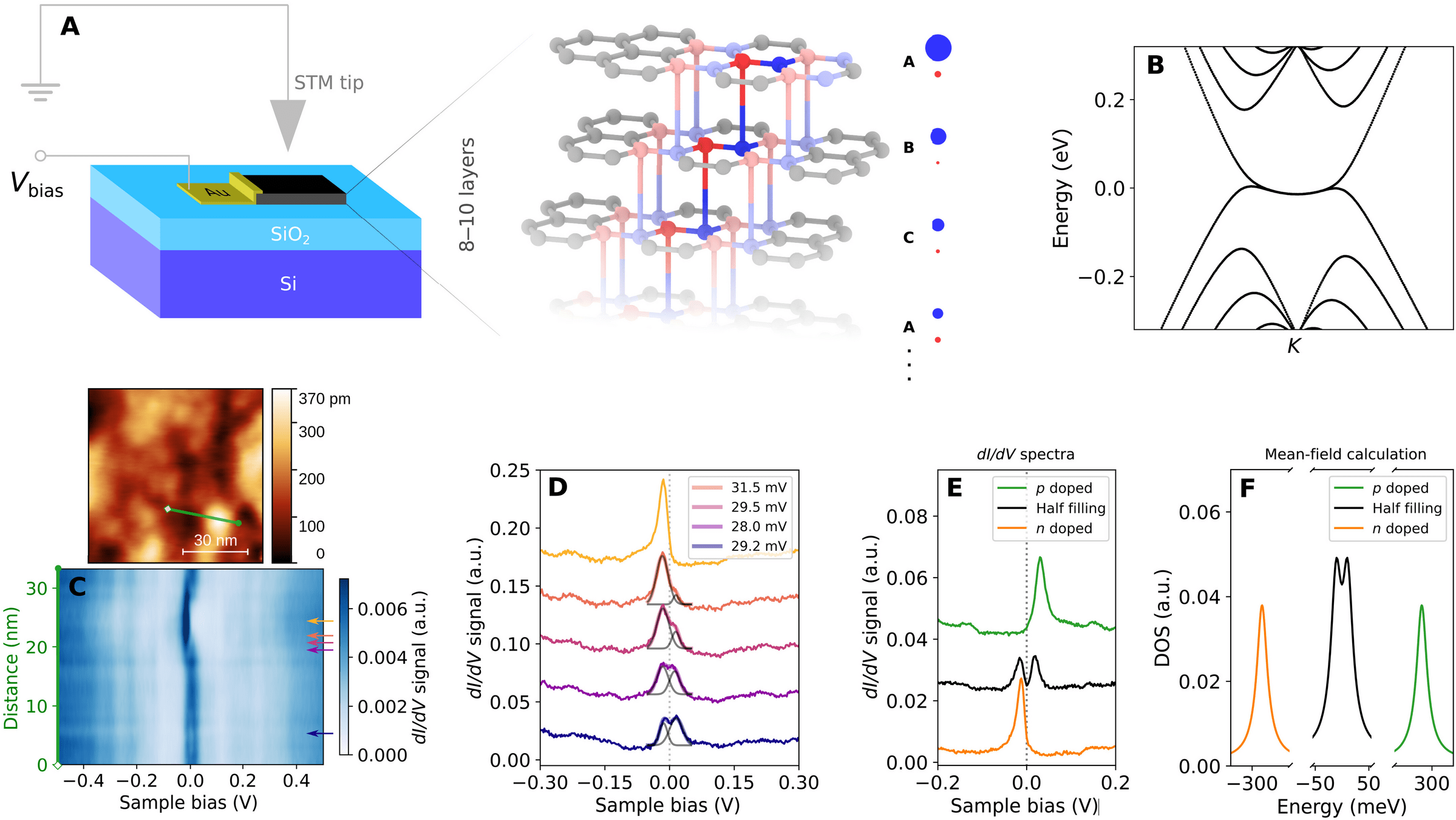
bitei / graphene
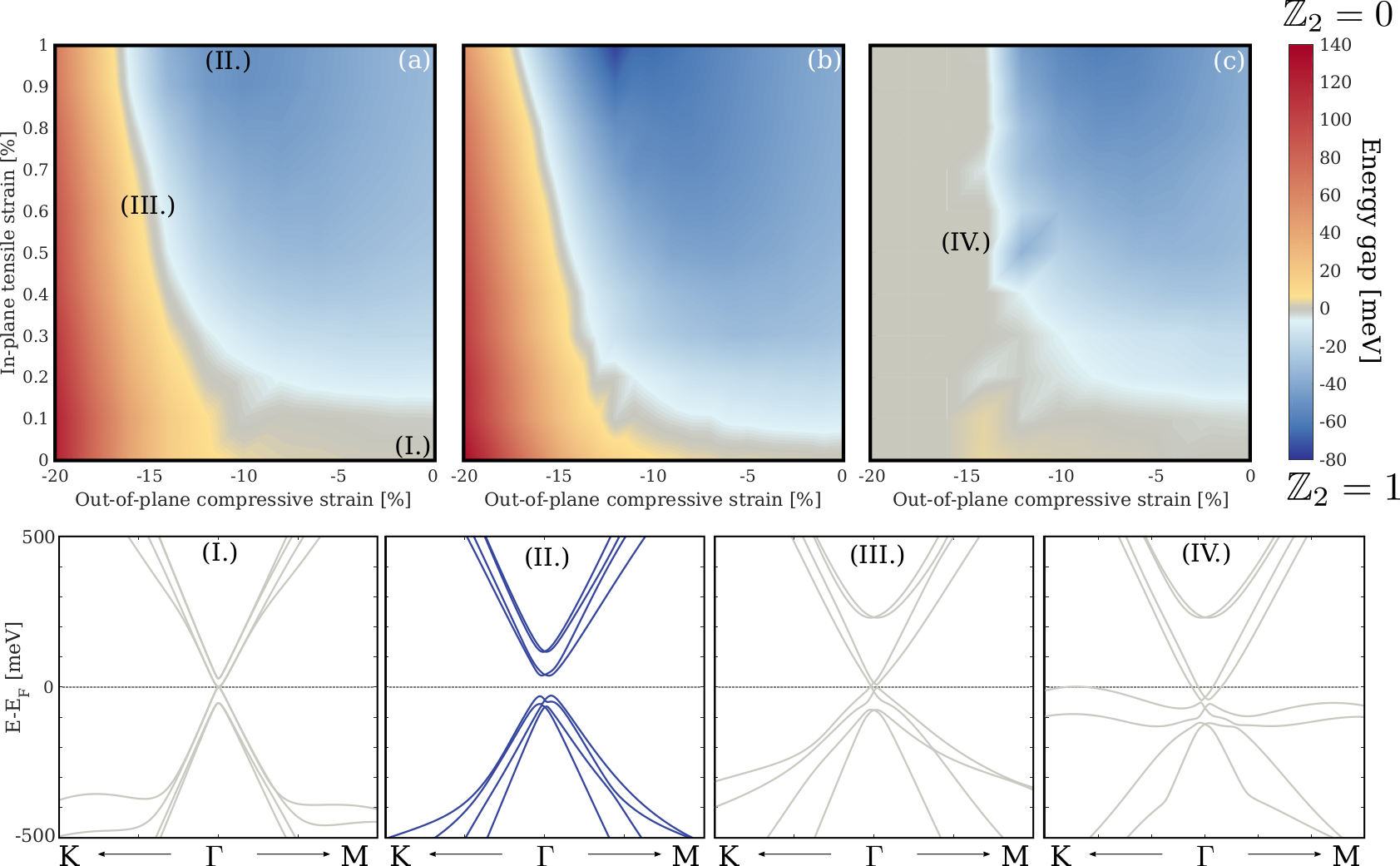
Mechanical strain induces topological phase transition in graphene / bitei heterostructures

zrte5
Using the SIESTA code we were able to clear out the confusion around the peculiar properties of ZrTe5


SIESTA

Capabilities
- Total and partial energies.
- Atomic forces.
- Geometry relaxation, fixed or variable cell.
- Spin polarized calculations (collinear or not).
- Local and orbital-projected density of states.
- Band structure.
- Model open-boundary systems (TRANS-SIESTA)
Standard DFT stuff

SIESTA

Capabilities
Model open-boundary systems (TRANS-SIESTA)
Standard DFT stuff

SIESTA

Capabilities
Model open-boundary systems (TRANS-SIESTA)
Standard DFT stuff


outline
siesta
Powerful DFT tool utilizing localized basis set. This means it provides a tight-binding Hamiltonian. Also models open-boundary systems.

bitei / graphene
Mechanical strain induce topological phase transition in graphene / bitei heterostructures

zrte5
Using the SIESTA code we were able to clear out the confusion around the peculiar properties of ZrTe5


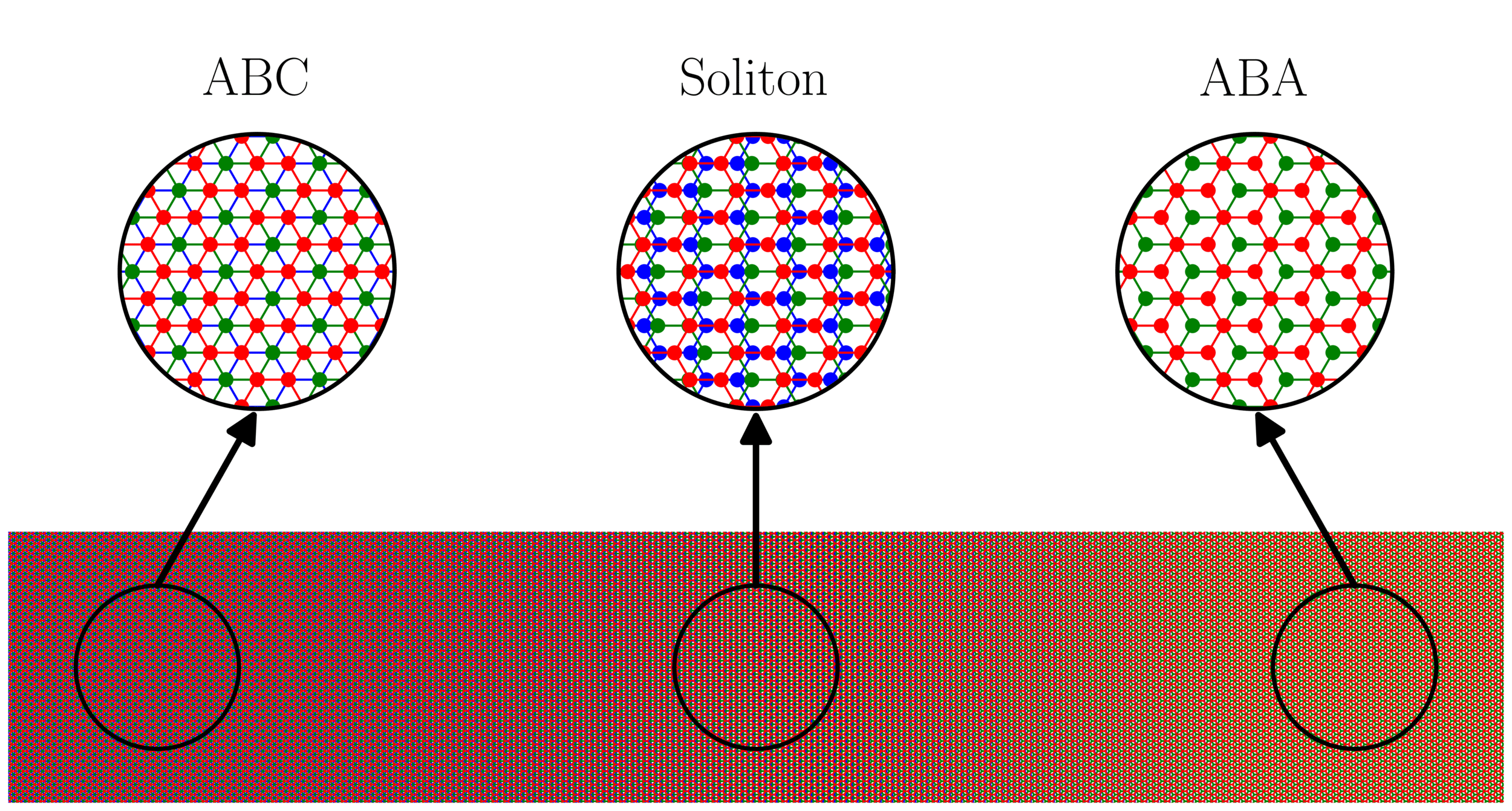
bitei / graphene systems


BiTeI sandwich: Kou et al. ACS Nano, 8 10448 (2014)
Z. Tajkov et al. Nanoscale 11, 12704 (2019)

bitei / graphene systems


BiTeI sandwich: Kou et al. ACS Nano, 8 10448 (2014)
Z. Tajkov et al. Nanoscale 11, 12704 (2019)



bitei / graphene systems


Z. Tajkov et al. Nanoscale 11, 12704 (2019)



Tini-Tiny
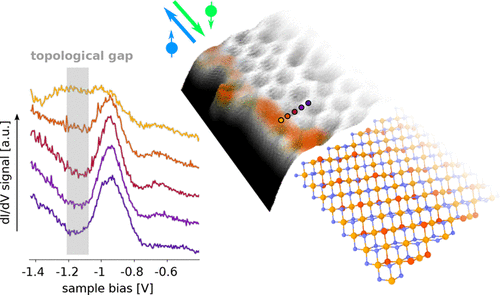
trivial gap

bitei / graphene systems


Z. Tajkov et al. Nanoscale 11, 12704 (2019)


Not so tiny
topological gap

in-plane strain
Tini-Tiny
trivial gap

bitei / graphene systems


Z. Tajkov et al. Appl. Sci. 2019, 9(20), 4330


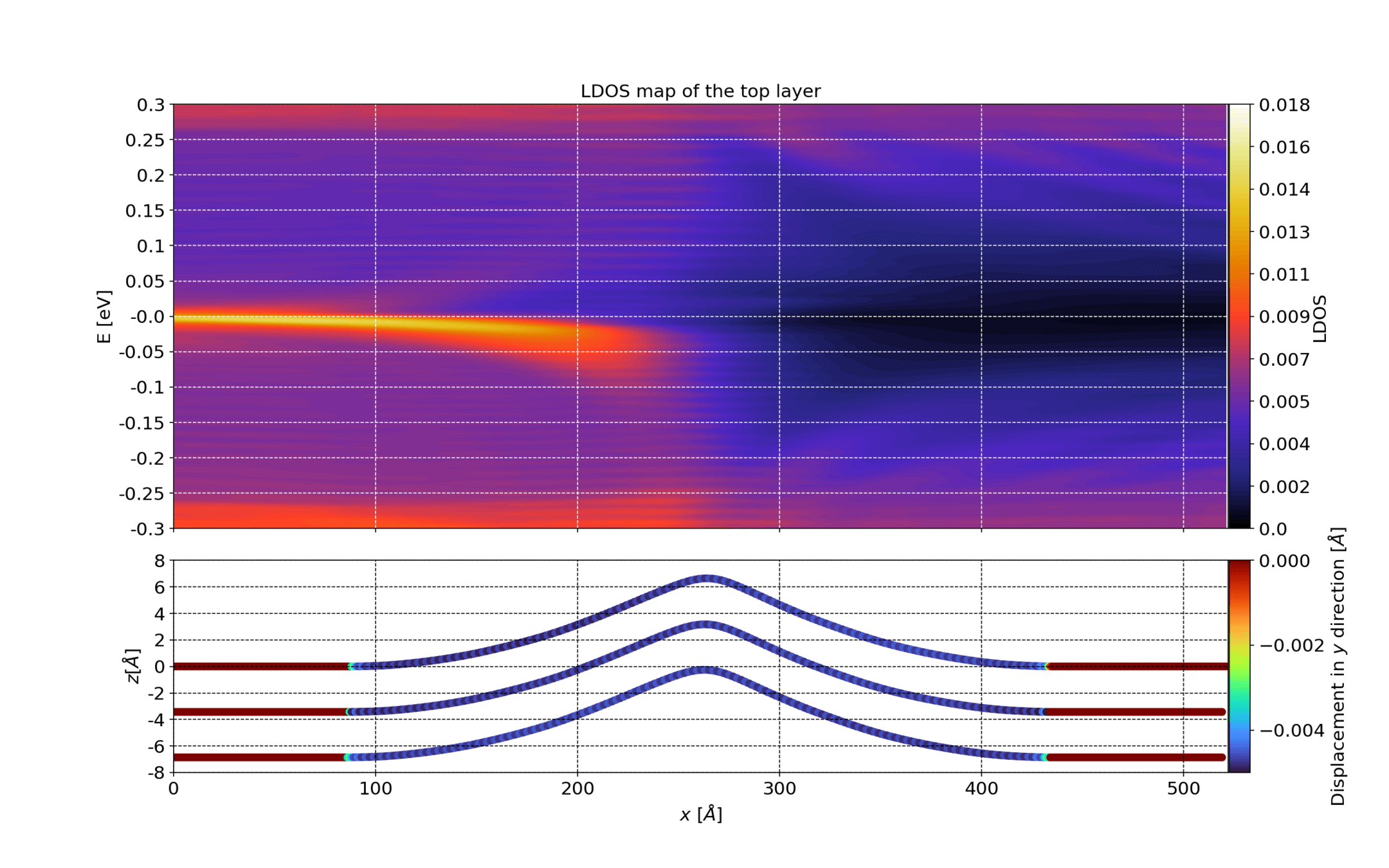
bitei / graphene systems


Z. Tajkov et al. Appl. Sci. 2019, 9(20), 4330
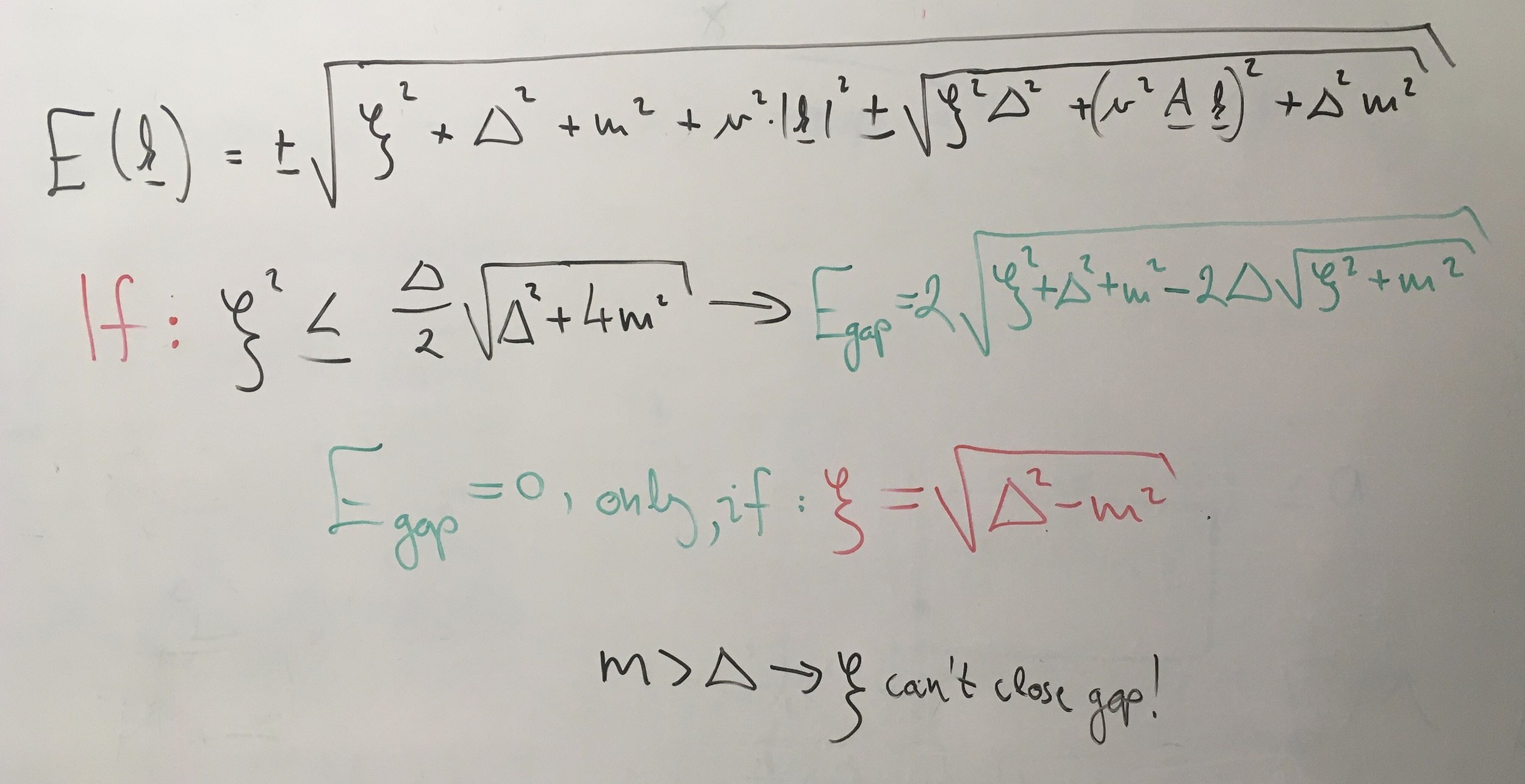
Tight-binding level

outline
siesta
Powerful DFT tool utilizing localized basis set. This means it provides a tight-binding Hamiltonian. Also models open-boundary systems.

bitei / graphene
Mechanical strain induce topological phase transition in graphene / bitei heterostructures

zrte5
Using the SIESTA code we were able to clear out the confusion around the peculiar properties of ZrTe5


zrte5


zrte5



zrte5

$$ \#1 $$
$$ \#2 $$
$$ d $$
$$ h$$
$$ R_1 $$
$$ R_2 $$
$$ Ang $$
55
49
1015
813
178
90
6000
4560


zrte5


$$ O_x $$
$$ \mathcal{A}_1 $$
$$ \mathcal{B}_1 $$
$$ C $$
$$ O_z$$
$$ O_x $$
$$ \mathcal{A}_1 $$
$$ \mathcal{B}_1 $$
$$ C $$
$$ O_z$$
Stiffness tensor (DFT)
Finite Element Method
Electric properties (DFT)


zrte5

COMSOL and DFT


zrte5

Ab initio


zrte5

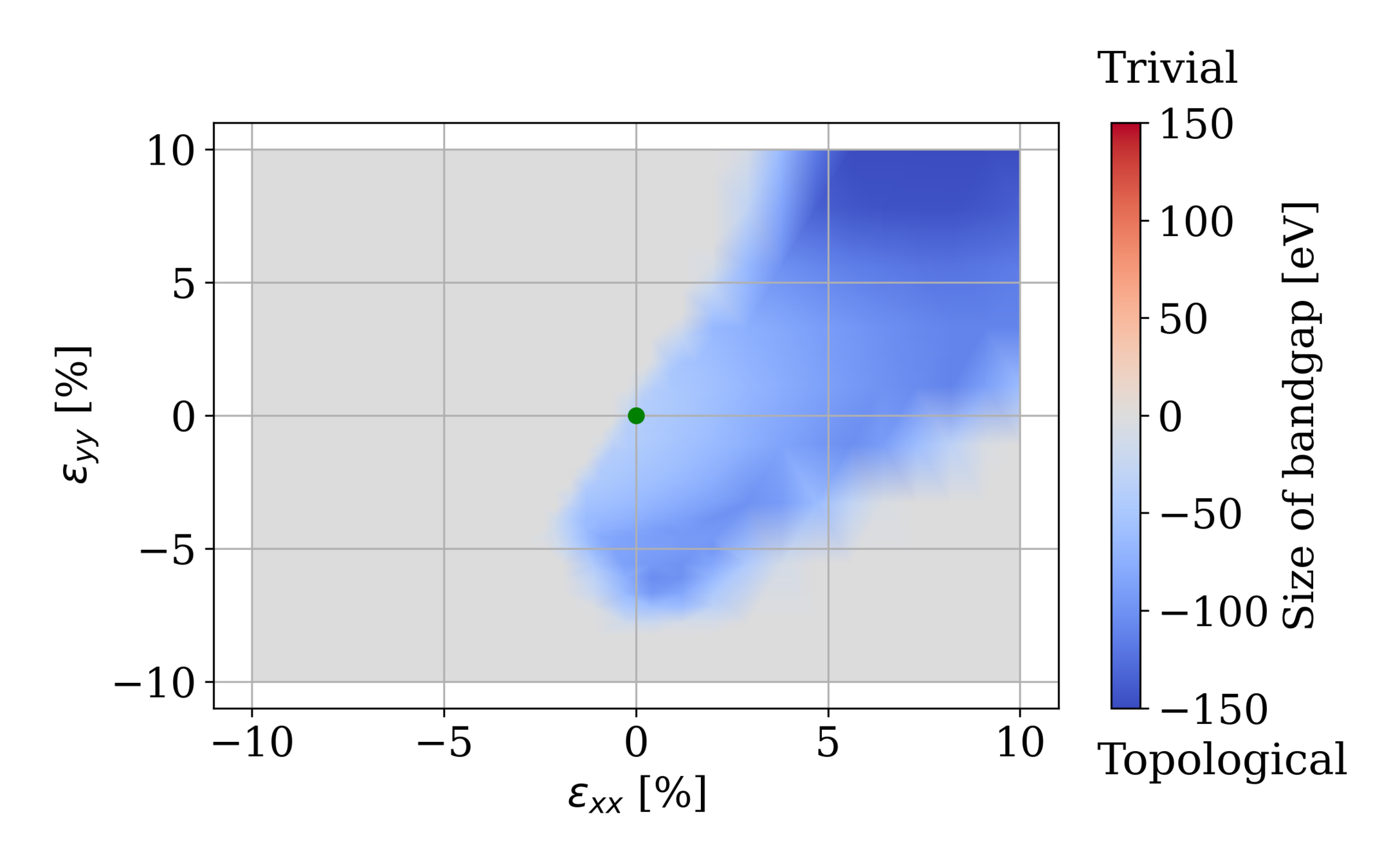
Monolayer

zrte5

Bilayer
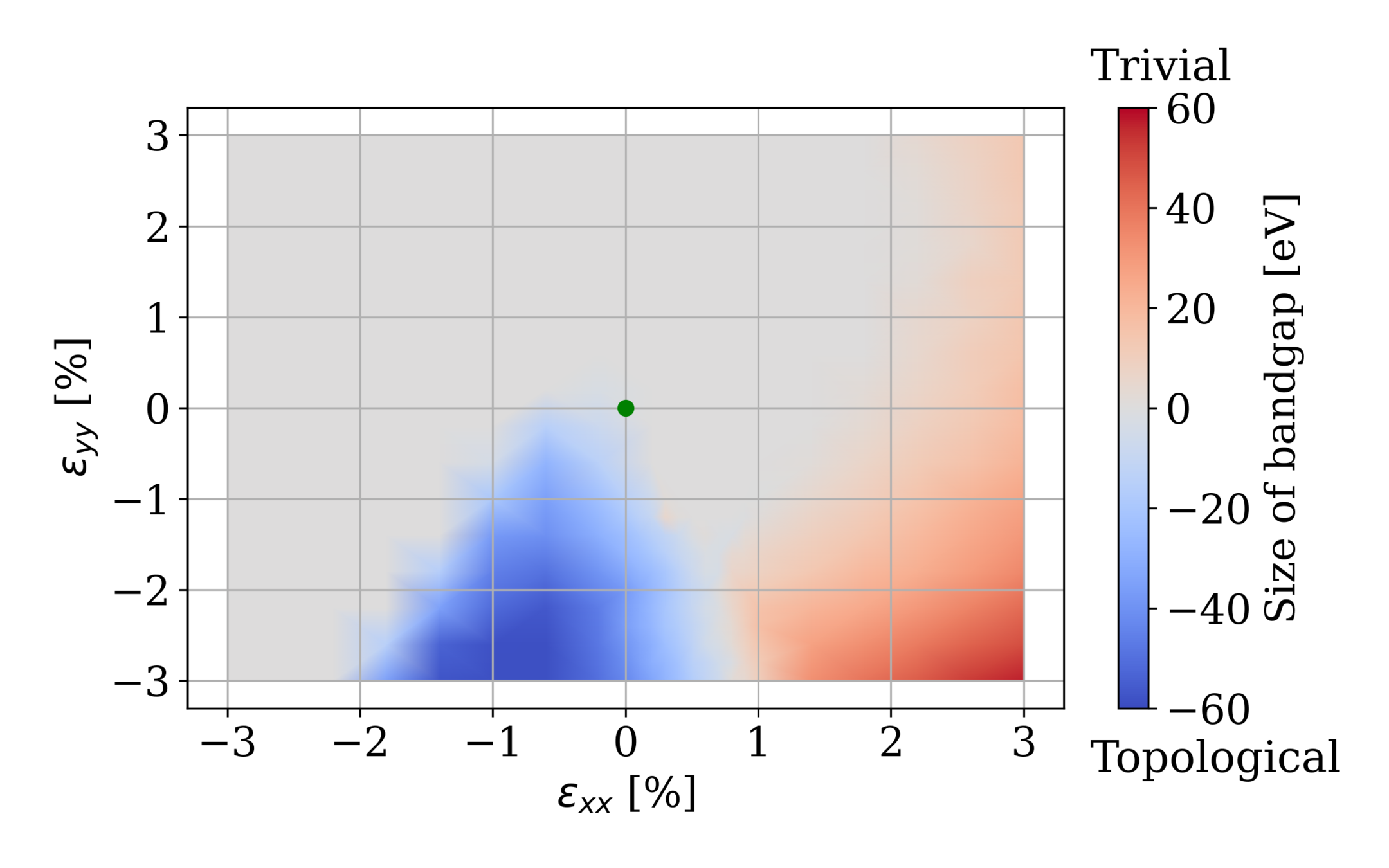

Phase diagrams



USING
SIESTA

Correlated states on the Hill

HUN-REN Centre for Energy Research
Capabilities in 2D
- Corralated states
- Topological states
- Small angle moiré
PEOPLE

Péter Nemes-Incze

Levente Tapasztó

Péter Vancsó