Logic, machines

&

sequent calculus

Alexander Gryzlov

Adform

19/12/2018

Lists

data List : Type -> Type where
  Nil  :                List a   -- aka []
  (::) : a -> List a -> List a

List membership

These are natural numbers in disguise!

data Elem : a -> List a -> Type where
  Here  :              Elem x (x::xs)
  There : Elem x xs -> Elem x (y::xs)

data Nat : Type where
  Z : Nat
  S : Nat -> Nat

ListS as sets

Subset : List a -> List a -> Type 
Subset {a} xs ys = 
  {x : a} -> Elem x xs -> Elem x ys

Lambda calculus

A formal rewriting system at the heart of FP

Untyped :

x (variable)
λx.M (abstraction)
M N (application)

+ β-reduction

(λx.M) N → M[x:=N]

untyped Lambda calculus

DeBrujin indices

Term0 : Term
Term0 = App (Lam $ App (Var Z) (Var Z)) 
            (Lam $ Var Z)

Term1 : Term
Term1 = App (App (Lam $ Var Z) (Lam $ Var Z))
            (Lam $ Var Z)

Term2 : Term
Term2 = App (Lam $ Var Z) 
            (App (Lam $ Var Z) (Lam $ Var Z))

data Term = Var Nat 
          | Lam Term
          | App Term Term

(λ x. x x) (λ x. x)

((λ x. x) (λ x. x)) 
(λ x. x)

(λ x. x) 
((λ x. x) (λ x. x))

untyped Lambda calculus

1.

(λ x. x x) (λ x. x)

(λ x. x) (λ x. x)

(λ x. x)

2.
((λ x. x) (λ x. x)) 
(λ x. x)

(λ x. x) (λ x. x)

(λ x. x)

3.

(λ x. x) 
((λ x. x) (λ x. x))

(λ x. x) (λ x. x)

(λ x. x)

simply-typed Lambda calculus

data Ty = A | Imp Ty Ty
infix 5 ~>
(~>) : Ty -> Ty -> Ty
(~>) = Imp

data Term : List Ty -> Ty -> Type where
  Var : Elem a g                  -> Term g a 
  Lam : Term (a::g) b             -> Term g (a~>b)
  App : Term g (a~>b) -> Term g a -> Term g b
    
TestTy : Ty
TestTy = A ~> A

-- Term1 not typeable because of self-application!
  
Term2 : Term [] TestTy
Term2 = App (App (Lam $ Var Here) (Lam $ Var Here)) (Lam $ Var Here)
  
Term3 : Term [] TestTy
Term3 = App (Lam $ Var Here) (App (Lam $ Var Here) (Lam $ Var Here))
  
Result : Term [] TestTy
Result = Lam $ Var Here

(structural) Proof theory

A branch of logic studying proofs as mathematical objects

Curry-Howard iso:

Theorem ~ Type

Proof ~ Term

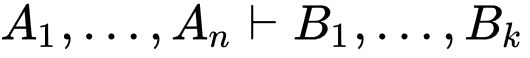
Sequent:

For now, let's restrict the RHS to a single formula:

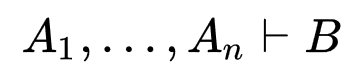
natural deduction

Minimal propositional logic:

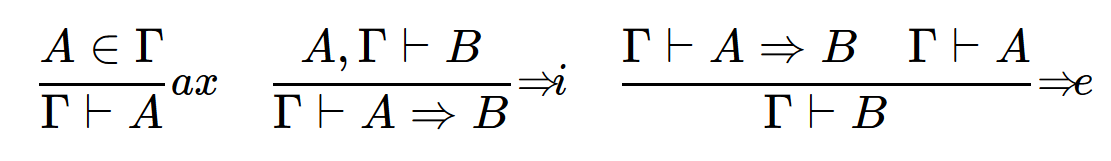
Var : 
Elem a g ->
Term g a

Lam :
Term (a::g) b ->
Term g (a~>b)

App : 
Term g (a~>b) ->
Term g a -> 
Term g b

Sequent calculus

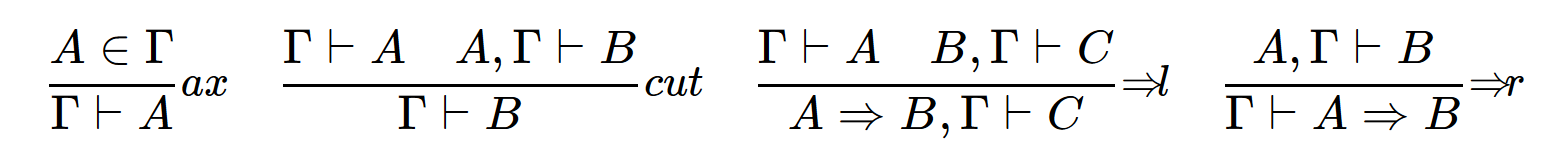
VarS : 
Elem a g -> 
TermS g a

Cut :
TermS g a ->
TermS (a::g) b ->
TermS g b

ImpL : 
TermS g a -> 
TermS (b::g) c -> 
TermS ((a~>b)::g) c

ImpR : 
TermS (a::g) b -> 
TermS g (a~>b)

structural properties

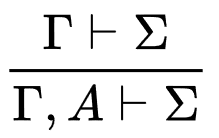
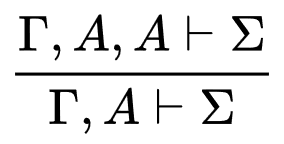
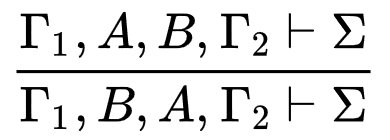
weakening contraction  permutation

Gentzen's LJ

data LJ : List Ty -> Ty -> Type where
  AxJ   : LJ [a] a
  CutJ  : LJ g a -> LJ (a::g) b -> LJ g b
  ImpLJ : LJ g a -> LJ (b::g) c -> LJ ((a~>b)::g) c
  ImpRJ : LJ (a::g) b -> LJ g (a~>b)
  WSJ   : LJ g b -> LJ (a::g) b
  CSJ   : LJ (a::a::g) b -> LJ (a::g) b
  PSJ   : LJ (g ++ a::b::d) c -> LJ (g ++ b::a::d) c

two-sided Sequent calculus

Splits sequents into kinds

and adds activation rules:

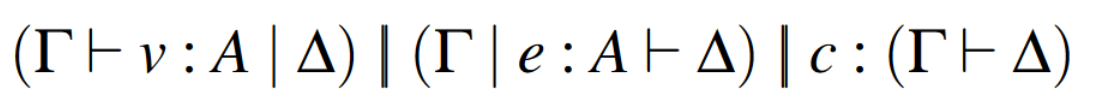
+ structural rules for both sides!

two-sided Sequent calculus

mutual 
  data Cmd : List Ty -> List Ty -> Type where 
    C : Term g a d -> CoTerm g a d -> Cmd g d
    CWL : ...
    CCL : ...
    CPL : ...
    CWR : ...

  data Term : List Ty -> Ty -> List Ty -> Type where
    Var : Term [a] a []
    Mu  : Cmd g (a::d) -> Term g a d
    ...

  data CoTerm : List Ty -> Ty -> List Ty -> Type where
    CoVar : CoTerm [] a [a]
    Mut   : Cmd (a::g) d -> CoTerm g a d
    ...

aka Gentzen's LK

two-sided Sequent calculus

mutual 
  data Cmd : List Ty -> List Ty -> Type where 
    C : Term g a d -> CoTerm g a d -> Cmd g d

  data Term : List Ty -> Ty -> List Ty -> Type where
    Var : Elem a g -> Term g a d
    Mu  : Cmd g (a::d) -> Term g a d

  data CoTerm : List Ty -> Ty -> List Ty -> Type where
    CoVar : Elem a d -> CoTerm g a d
    Mut   : Cmd (a::g) d -> CoTerm g a d

internalise structurals

Subset : List a -> List a -> Type
Subset {a} xs ys = {x : a} -> Elem x xs -> Elem x ys

data IsSubset : List a -> List a -> Type where 
  Id    :                 IsSubset     l      l    
  Cons2 : IsSubset l m -> IsSubset (a::l) (a::m) 

shift : IsSubset l m -> Subset l m  
shift  Id        el        = el
shift (Cons2 s)  Here      = Here
shift (Cons2 s) (There el) = There $ shift s el 

mutual    
  shiftCmd : IsSubset g g1 -> IsSubset d d1 
          -> Cmd g d -> Cmd g1 d1    

  shiftTerm : IsSubset g g1 -> IsSubset d d1 
           -> Term g a d -> Term g1 a d1    

  shiftCoTerm : IsSubset g g1 -> IsSubset d d1 
             -> CoTerm g a d -> CoTerm g1 a d1

Connectives

E.g., we can add function, tuples & discriminated unions:

data Ty = A | Imp Ty Ty | Prod Ty Ty | Sum Ty Ty

mutual 
  data Cmd : List Ty -> List Ty -> Type where 
    C : Term g a d -> CoTerm g a d -> Cmd g d

  data Term : List Ty -> Ty -> List Ty -> Type where
    Var  : Elem a g -> Term g a d
    Mu   : Cmd g (a::d) -> Term g a d
    Lam  : Term (a::g) b d -> Term g (Imp a b) d
    Pair : Term g a d -> Term g b d -> Term g (Prod a b) d
    Inl  : Term g a d -> Term g (Sum a b) d
    Inr  : Term g b d -> Term g (Sum a b) d

  data CoTerm : List Ty -> Ty -> List Ty -> Type where
    CoVar : Elem a d -> CoTerm g a d
    Mut   : Cmd (a::g) d -> CoTerm g a d
    AppC  : Term g a d -> CoTerm g b d -> CoTerm g (Imp a b) d
    MatP  : Cmd (a::b::g) d -> CoTerm g (Prod a b) d
    MatS  : Cmd (a::g) d -> Cmd (b::g) d -> CoTerm g (Sum a b) d

Abstract machines

Like a virtual machine, but abstract :)

Usually includes closures, stacks & environments

KRivine Abstract machine

Lazy (call by name)

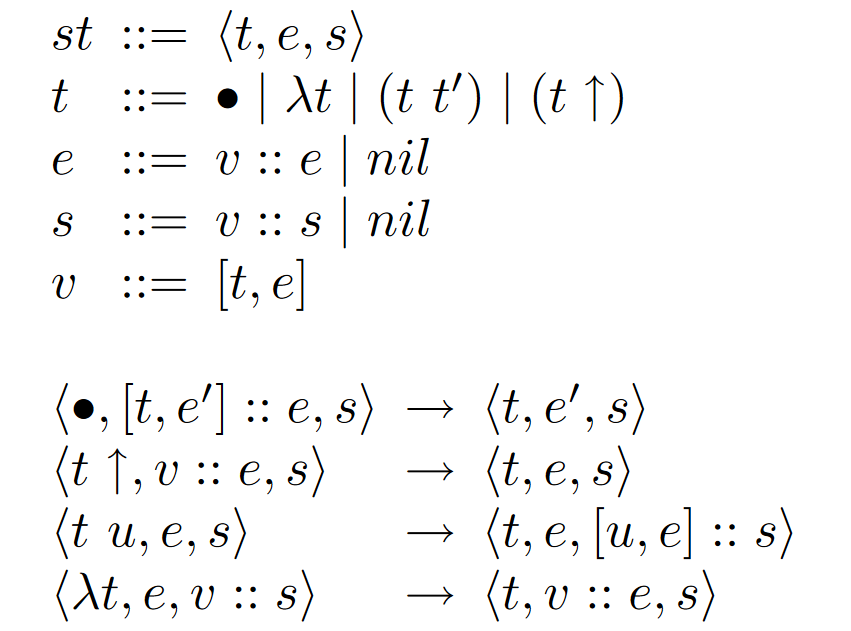
KRivine Abstract machine

mutual
  Env : Type 
  Env = List Clos

  data Clos = Cl Term Env

Stack : Type
Stack = List Clos

State : Type
State = (Term, Env, Stack)

step : State -> Maybe State
step (Var  Z   , Cl t e::_,    s) = Just (    t,    e,         s)
step (Var (S n),      _::e,    s) = Just (Var n,    e,         s)
step (Lam t    ,         e, c::s) = Just (    t, c::e,         s)
step (App t u  ,         e,    s) = Just (    t,    e, Cl u e::s)
step  _                           = Nothing

cek

Control + Environment + Kontinuation

Eager (call by value)

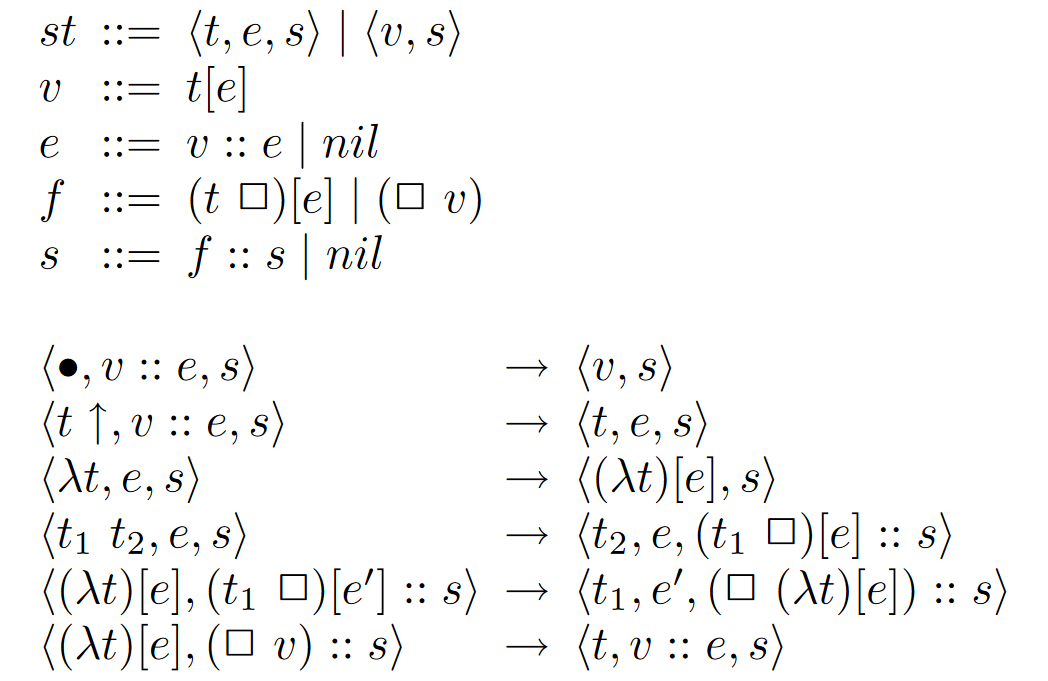
cek

mutual
  Env : Type 
  Env = List Clos

  data Clos = Cl Term Env

data Frame = Fun Term Env | Arg Clos

Stack : Type
Stack = List Frame

data State = L Term Env Stack | R Clos Stack

step : State -> Maybe State
step (L (Var  Z)    (v::_)            s ) = Just $ R  v                                  s
step (L (Var (S n)) (_::e)            s ) = Just $ L (Var n)     e                       s
step (L (Lam t)         e             s ) = Just $ R (Cl (Lam t) e)                      s
step (L (App t u)       e             s ) = Just $ L u           e             (Fun t e::s)
step (R (Cl (Lam t)    e) (Fun t1 e1::s)) = Just $ L t1          e1 (Arg (Cl (Lam t) e)::s)
step (R (Cl (Lam t)    e) (    Arg v::s)) = Just $ L t       (v::e)                      s
step  _                                   = Nothing

Deconstructing

application, lambdas & LET

(λx.t) u → t[x:=u]
<λx.t | u·e> → <t[x:=u] | e>

<μ(x·α).c | u·e> → c[x:=u,α:=e]

λx.t === μ(x·α).<t|α>

<t u | e> → <t | u·e>

<μα.c | e> → c[α:=e]

t u === μα.<t|u·α>

let x=t in u   ===   μα.<t|μ~x.<u|α>>

Deconstructing

application & lambdas

mutual 
  data Cmd : List Ty -> List Ty -> Type where 
    C : Term g a d -> CoTerm g a d -> Cmd g d

  data Term : List Ty -> Ty -> List Ty -> Type where
    Var  : Elem a g -> Term g a d
    Mu   : Cmd g (a::d) -> Term g a d
    MatC : Cmd (a::g) (b::d) -> Term g (Imp a b) d

  data CoTerm : List Ty -> Ty -> List Ty -> Type where
    CoVar : Elem a d -> CoTerm g a d
    Mut   : Cmd (a::g) d -> CoTerm g a d
    AppC  : Term g a d -> CoTerm g b d -> CoTerm g (Imp a b) d

lam : Term (a::g) b d -> Term g (Imp a b) d
lam t = 
  MatC $ C (shiftTerm t) (CoVar Here)

app : Term g (Imp a b) d -> Term g a d -> Term g b d
app t u = 
  Mu $ 
  C (shiftTerm t) (AppC (shiftTerm u) (CoVar Here))

let_ : Term g a d -> Term (a::g) b d -> Term g b d    
let_ t u = Mu $ C (shiftTerm t) 
                  (Mut $ C (shiftTerm u) (CoVar Here))

call/cc

callcc : Term g (Imp (Imp a b) a) (a::d) -> Term g a d
callcc f = 
  Mu $ C f
         (AppC 
           (MatC $ C (Var Here) (CoVar $ There Here))
           (CoVar Here))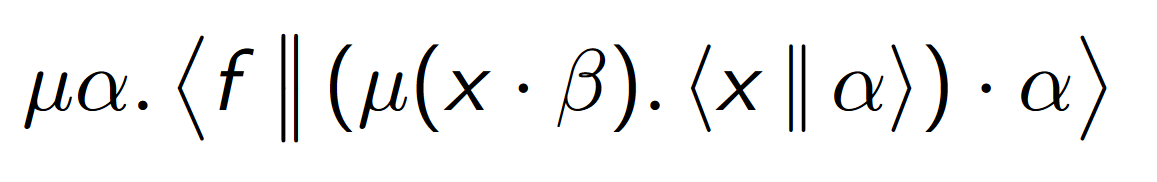

reduction

reduce : Cmd g d -> Maybe (Cmd g d)
reduce (C (Mu c)    e        ) = Just $ cosubst c e
reduce (C  t       (Mut c)   ) = Just $ subst c t
reduce (C (MatC c) (AppC t e)) = Just $ subst 
                                        (cosubst c (shiftCoTerm e)) 
                                        (shiftTerm t)
reduce  _                      = Nothing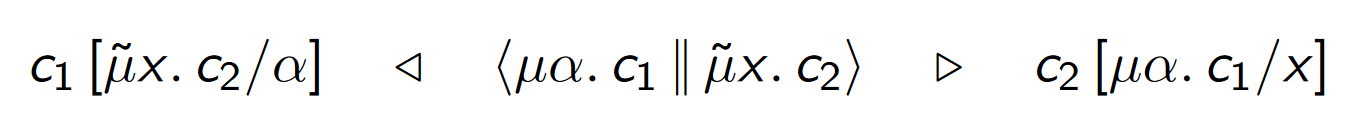

critical pair!

Dual reduction - LKT

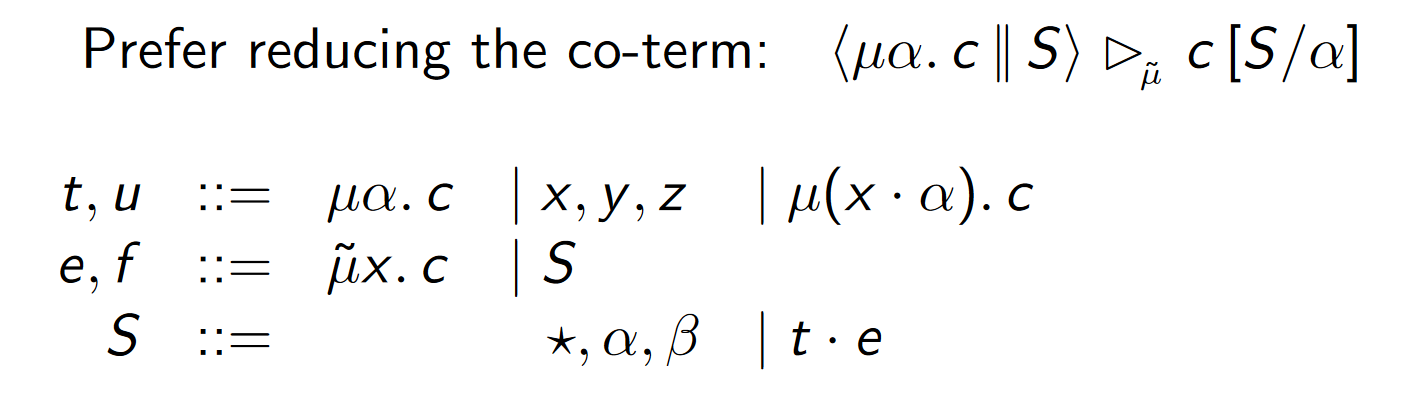
Amounts to lazy evaluation

Dual reduction - LKT

mutual 
  data Cmd : List Ty -> List Ty -> Type where 
    C : Term g a d -> CoTerm g a d -> Cmd g d

  data Term : List Ty -> Ty -> List Ty -> Type where
    Var  : Elem a g -> Term g a d
    Mu   : Cmd g (a::d) -> Term g a d
    MatC : Cmd (a::g) (b::d) -> Term g (Imp a b) d

  data CoTerm : List Ty -> Ty -> List Ty -> Type where
    CoVal : CoValue g a d -> CoTerm g a d
    Mut   : Cmd (a::g) d -> CoTerm g a d

  data CoValue : List Ty -> Ty -> List Ty -> Type where
    Empty : CoValue g a d
    CoVar : Elem a d -> CoValue g a d
    AppC  : Term g a d -> CoValue g b d 
         -> CoValue g (Imp a b) d

Dual reduction - LKQ

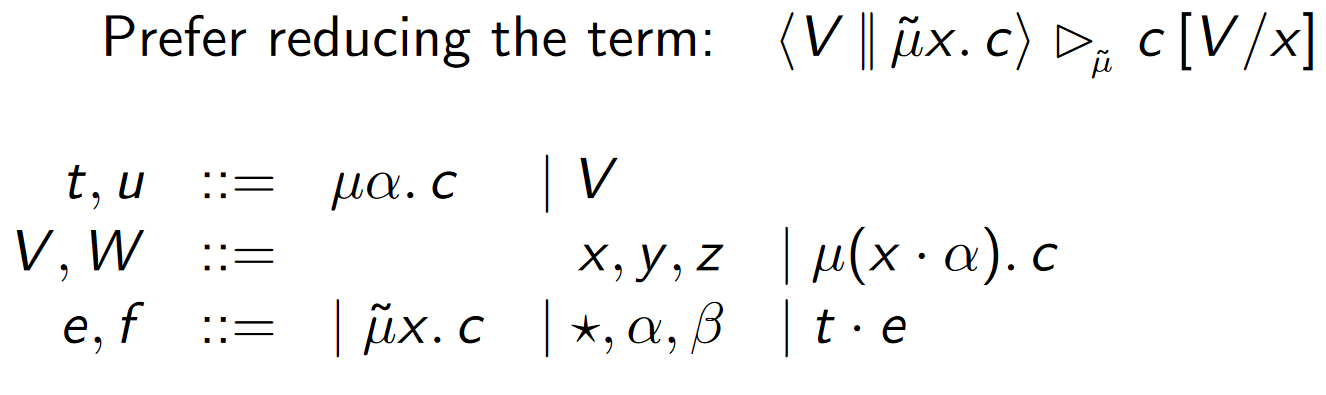
Amounts to eager evaluation

Dual reduction - LKQ

mutual 
  data Cmd : List Ty -> List Ty -> Type where 
    C : Term g a d -> CoTerm g a d -> Cmd g d

  data Term : List Ty -> Ty -> List Ty -> Type where
    Val  : Value g a d -> Term g a d
    Mu   : Cmd g (a::d) -> Term g a d

  data Value : List Ty -> Ty -> List Ty -> Type where
    Var  : Elem a g -> Value g a d
    MatC : Cmd (a::g) (b::d) -> Value g (Imp a b) d

  data CoTerm : List Ty -> Ty -> List Ty -> Type where
    CoVar : Elem a d -> CoTerm g a d
    Empty : CoTerm g a d
    Mut   : Cmd (a::g) d -> CoTerm g a d
    AppC  : Value g a d -> CoTerm g b d 
         -> CoTerm g (Imp a b) d

Polarization

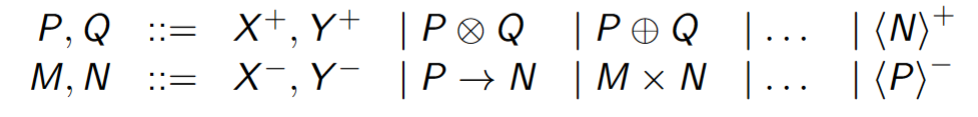
Types

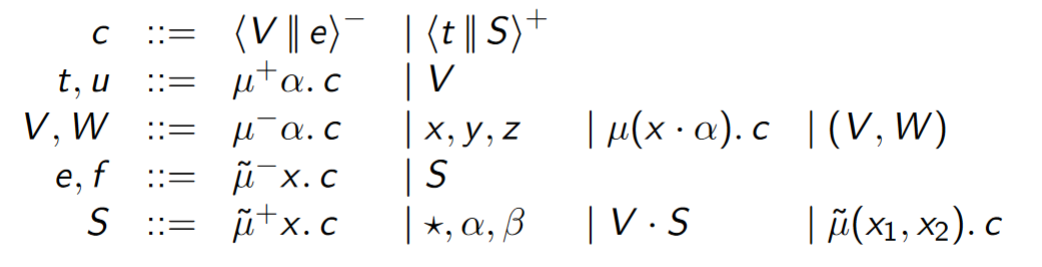
Terms

more polarities

call by need! (true laziness)

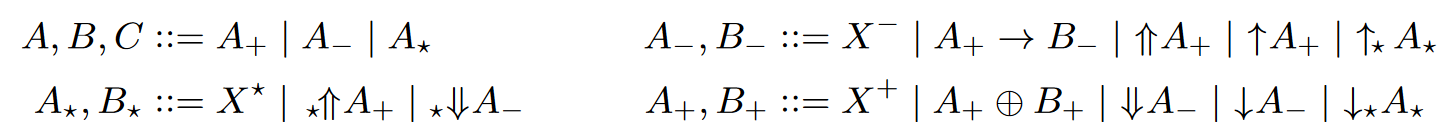
effects

reduce : Monad m => Cmd g d -> m (Cmd g d)
...



Adjunction f g => Monad (Compose g f)
???

generalizing connectives

Move to

inductive sums of products and
coinductive records of functions/matches

Infinite structures become first class

polymorphism

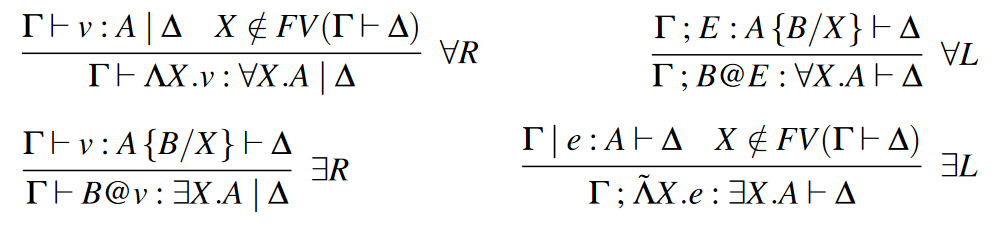
Both universal and existential

dependent types

Literature

Thanks!

https://github.com/clayrat/sequent-calc