Pistejoukon yhtälö
Suoran jokaisen pisteen (x, y) koordinaatit toteuttavat suoran yhtälön
Tason jokainen piste (x, y), joka toteuttaa suoran yhtälön on suoralla.
Pistejoukon yhtälö
Pistejoukon yhtälö on muuttujien x ja y yhtälö, jolla on seuraava ominaisuus:
Piste (x, y) kuuluu pistejoukkoon jos ja vain jos pisteen koordinaatit toteuttavat yhtälön.
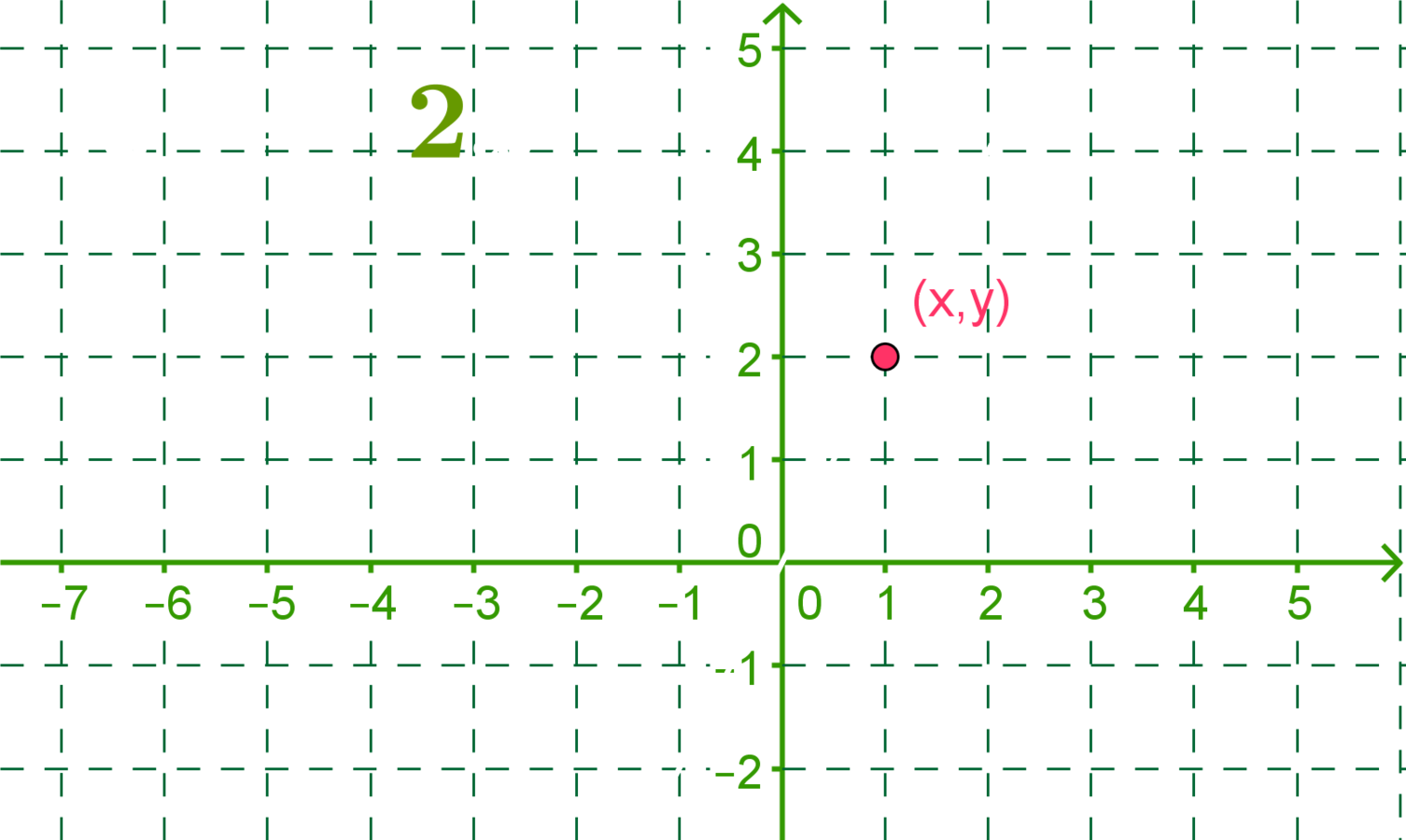
Piste (x, y) on suoralla jos ja vain jos y = 2x
Esim.
Esimerkki
Pistejoukon yhtälö on
-y^3+x^2+3=0
−y3+x2+3=0
Onko piste (1, -1) pistejoukossa?
Onko piste (2, -1) pistejoukon ala- vai yläpuolella?
a)
b)
Ratkaisu a-kohtaan
Piste (1, -1) on pistejoukossa jos se toteuttaa pistejoukon yhtälön.
-y^3+x^2+3=0
−y3+x2+3=0
-(-1)^3+1^2+3=0
−(−1)3+12+3=0
1+1+3=0
1+1+3=0
Sijoitetaan x = 1 ja y = -1 pistejoukon yhtälöön.
5=0
5=0
Epätosi
||x=1, \ y=-1
∣∣x=1, y=−1
Piste (1, -1) ei ole pistejoukossa.
Ratkaisu b-kohtaan
Ratkaistaan pistejoukon pisteen y-koordinaatti, kun x-koordinaatti on 2.
-y^3+x^2+3=0
−y3+x2+3=0
||x=2
∣∣x=2
-y^3+2^2+3=0
−y3+22+3=0
-y^3+7=0
−y3+7=0
y^3=7
y3=7
Pistejoukon piste
on pisteen (2,-1) yläpuolella.