Esimerkki
Ratkaise yhtälö
a)
|x|=10
∣x∣=10
|2x+4|=7
∣2x+4∣=7
b)
Ratkaisu a-kohtaan
x \geq 0
x≥0
1.
x < 0
x<0
2.
|x|=10
∣x∣=10
||x \geq 0
∣∣x≥0
x=10
x=10
|x|=10
∣x∣=10
||x <0
∣∣x<0
x=-10
x=−10
Vastaus:
x=10 \text{ tai } x=-10
x=10 tai x=−10
Ratkaisu b-kohtaan
2x+4 \geq 0
2x+4≥0
1.
2x+4 < 0
2x+4<0
2.
|2x+4|=7
∣2x+4∣=7
||x \geq -2
∣∣x≥−2
2x+4=7
2x+4=7
|2x+4|=7
∣2x+4∣=7
||x <-2
∣∣x<−2
2x \geq-4
2x≥−4
x \geq-2
x≥−2
2x < -4
2x<−4
x < -2
x<−2
2x=3
2x=3
x=\dfrac{3}{2}
x=23
2x+4=-7
2x+4=−7
2x=-11
2x=−11
x=-\dfrac{11}{2}
x=−211
||:2
∣∣:2
||:2
∣∣:2
Vastaus:
x=\dfrac{3}{2} \text{ tai } x=-\dfrac{11}{2}
x=23 tai x=−211
Graafinen ratkaisu
"\text{abs}(x) "
"abs(x)"
"\text{abs}(2x+4) "
"abs(2x+4)"
Itseisarvoyhtälö
|f(x)|=a, \ a \geq 0
∣f(x)∣=a, a≥0
f(x)=a
f(x)=a
f(x)=-a
f(x)=−a
tai
|f(x)|=a, \ a<0
∣f(x)∣=a, a<0
Yhtälöllä ei ole ratkaisua, sillä luvun itseisarvo on aina epänegatiivinen.
Itseisarvoyhtälön ratkaiseminen:
1.
2.
Esimerkki
Ratkaise yhtälö
|5x-10|-3=0
∣5x−10∣−3=0
ratkaisu
|5x-10|-3=0
∣5x−10∣−3=0
|5x-10|=3
∣5x−10∣=3
5x-10=-3
5x−10=−3
tai
tai
5x-10=3
5x−10=3
5x=13
5x=13
5x=7
5x=7
x=\dfrac{13}{5}
x=513
tai
x=\dfrac{7}{5}
x=57
Esimerkki
|x|<5
∣x∣<5
|2x+1|\geq 3
∣2x+1∣≥3
Ratkaise epäyhtälö
a)
b)
Ratkaisu A-kohtaan
|x|<5
∣x∣<5
Luvut joiden itseisarvo on pienempi kuin 5, ovat lukusuoralla lukujen -5 ja 5 välissä.
-5 < x<5
−5<x<5
tai yhtäpitävästi voidaan merkitä
] -5, 5 [
]−5,5[
Ratkaisu B-kohtaan
|2x+1|\geq3
∣2x+1∣≥3
2x+1 \geq 3
2x+1≥3
2x+1 \leq -3
2x+1≤−3
2x\geq 2
2x≥2
x\geq 1
x≥1
2x\leq -4
2x≤−4
x\leq -2
x≤−2
tai
tai
tai
||:2 \ (>0)
∣∣:2 (>0)
Itseisarvoepäyhtälö
|f(x)|< \color{Salmon}{a}, \text{ kun } \color{Salmon}{a} >0
∣f(x)∣<a, kun a>0
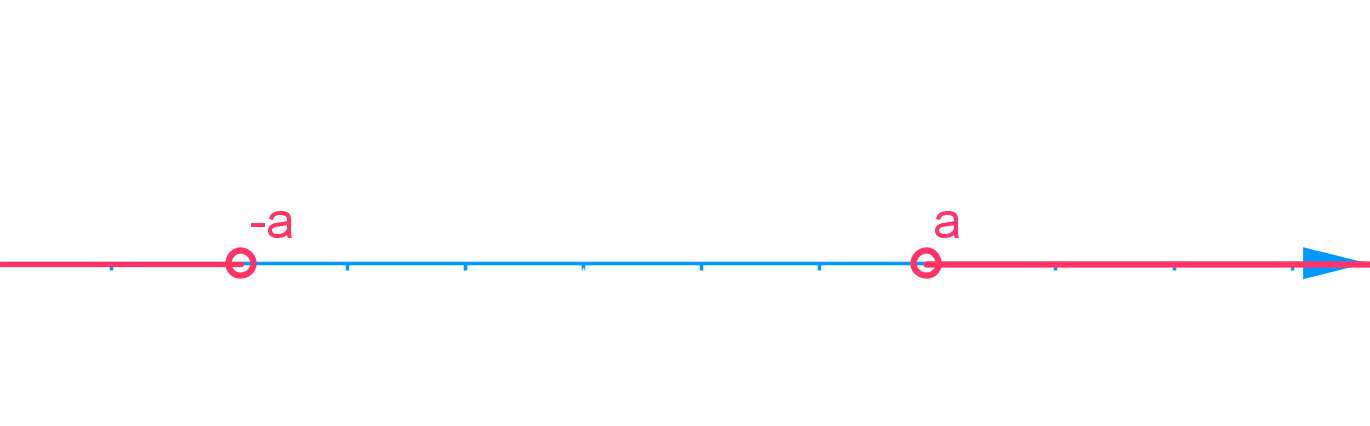
\color{Salmon}{-a} < f(x) < \color{Salmon}{a}
−a<f(x)<a
|f(x)|> \color{Salmon}{a}, \text{ kun } \color{Salmon}{a} >0
∣f(x)∣>a, kun a>0
f(x)<\color{Salmon}{-a} \text{ tai } f(x)>\color{Salmon}{-a}
f(x)<−a tai f(x)>−a
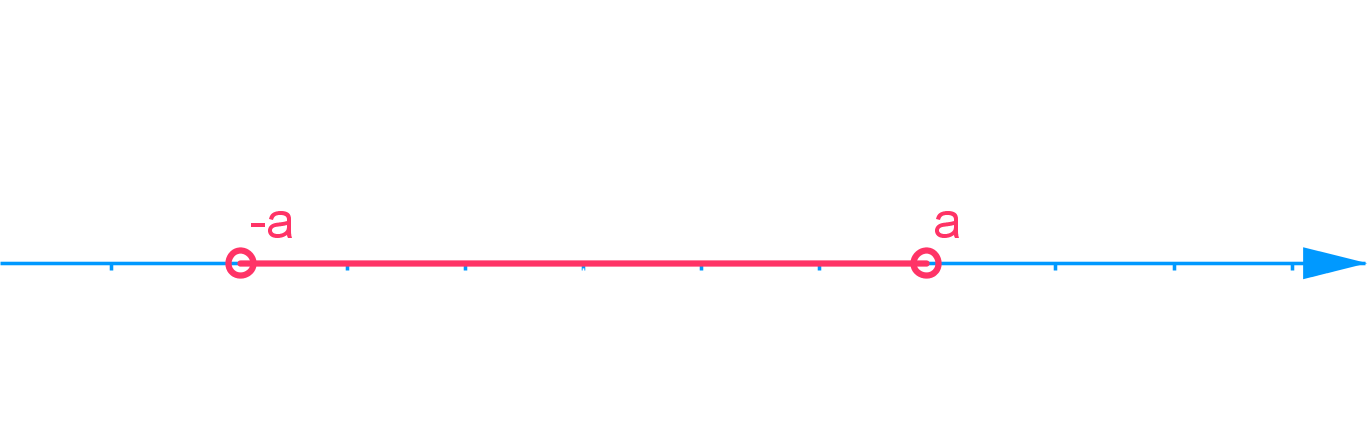
f(x) >\color{Salmon}{-a}\text{ ja } f(x)< \color{Salmon}{a}
f(x)>−a ja f(x)<a
Esimerkki
Ratkaise epäyhtälö
|x^2-4|<3
∣x2−4∣<3
Ratkaisu
|x^2-4|<3
∣x2−4∣<3
-3 < x^2-4<3
−3<x2−4<3
-3 < x^2-4
−3<x2−4
x^2-4<3
x2−4<3
ja
1< x^2
1<x2
x^2<7
x2<7
ja
x^2-1=0
x2−1=0
x=\pm 1
x=±1
x^2-7=0
x2−7=0
x=\pm \sqrt{7}
x=±√7
-1
−1
1
1
-\sqrt{7}
−√7
\sqrt{7}
√7
1 < x^2
1<x2
x^2<7
x2<7
T
T
T
T
E
T
T
T
E
E
Tapa 1
Vastaus:
Epäyhtälö
|x^2-4|<3
∣x2−4∣<3
toteutuu, kun
-\sqrt{7} < x<-1 \text{ tai } 1 < x < \sqrt{7}
−√7<x<−1 tai 1<x<√7
1 < x^2
1<x2
x^2<7
x2<7
Tapa 2
ylöspäin
aukeava
paraabeli
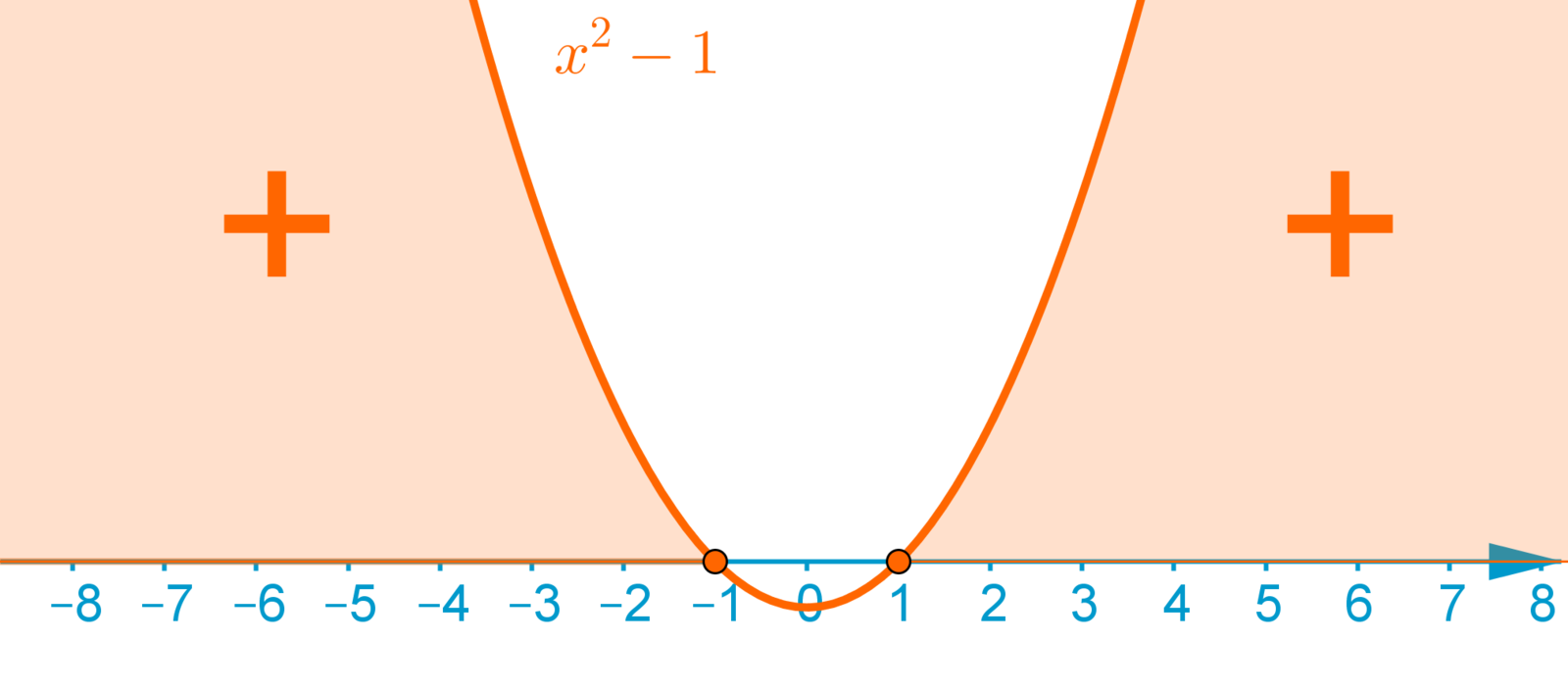
0 < x^2-1
0<x2−1
x^2-7<0
x2−7<0
x^2-1=0
x2−1=0
x=\pm 1
x=±1
x^2-7=0
x2−7=0
x=\pm \sqrt{7}
x=±√7
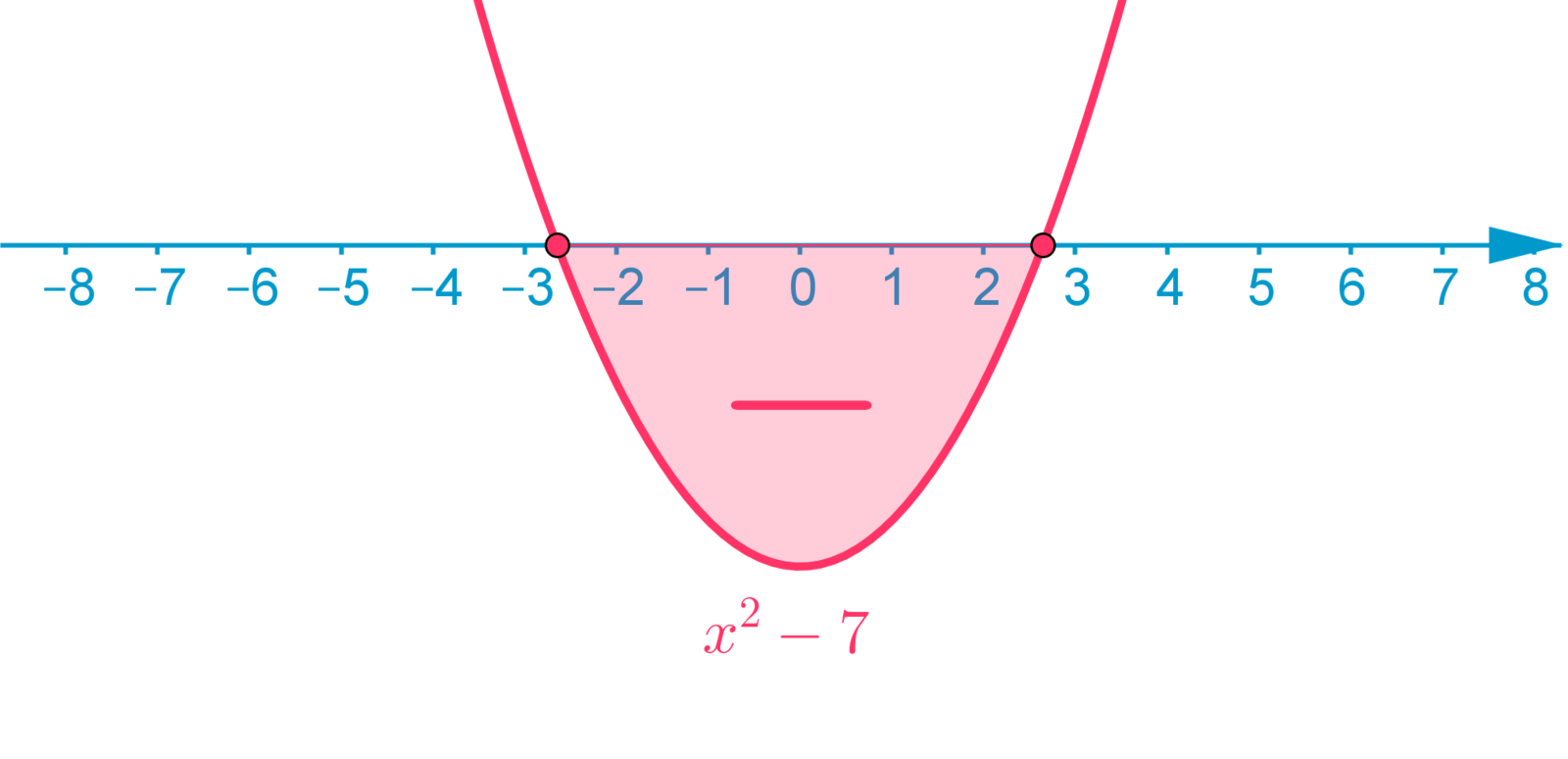
x^2-7<0
x2−7<0
0 < x^2-1
0<x2−1
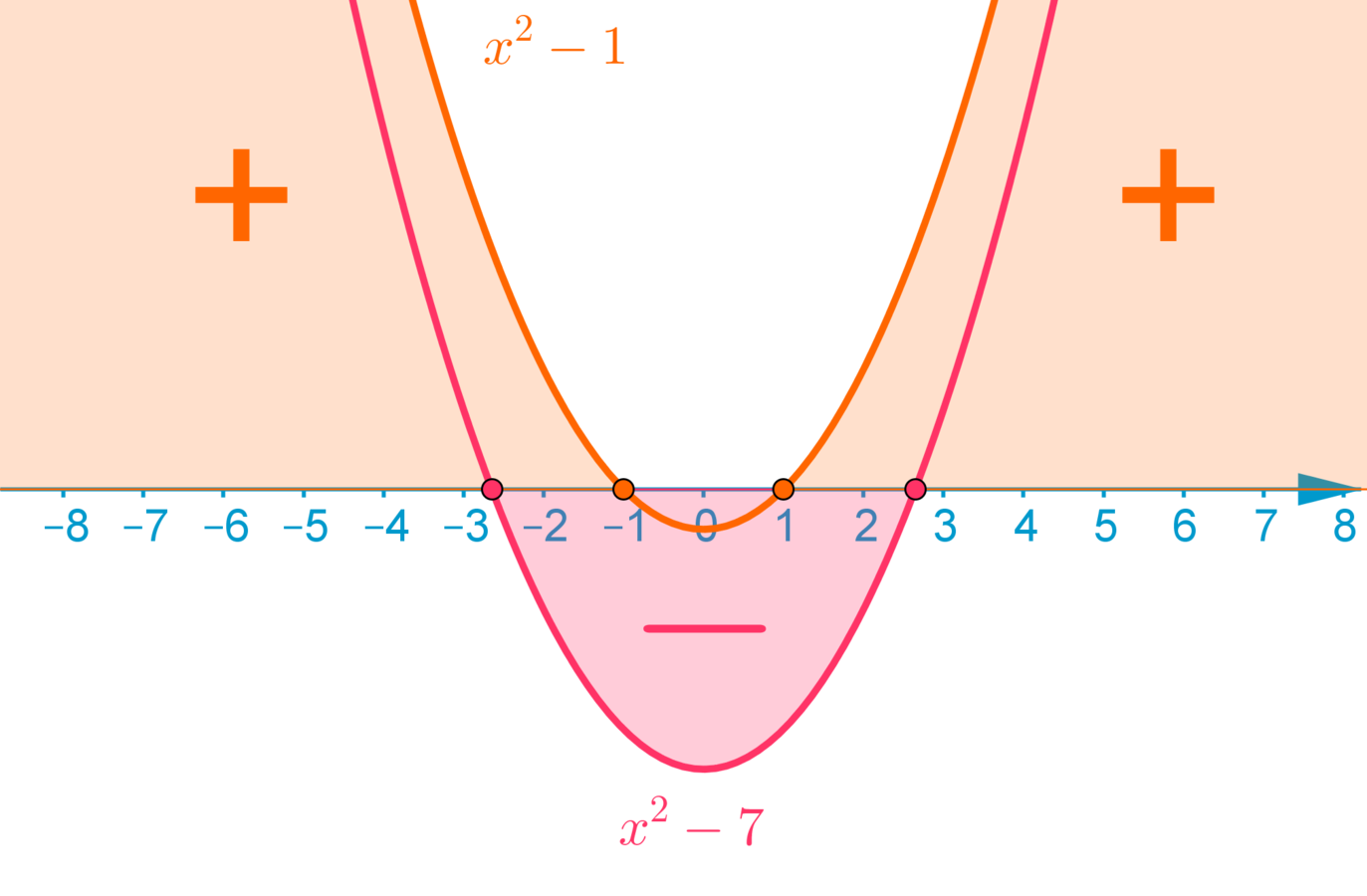
Vastaus:
Epäyhtälö
|x^2-4|<3
∣x2−4∣<3
toteutuu, kun
-\sqrt{7} < x<-1 \text{ tai } 1 < x < \sqrt{7}
−√7<x<−1 tai 1<x<√7