Suureet ja maailmankaikkeuden kokoluokat
Maailmankaikkeuden pienet rakenteet
"Kyse on vain aikaskaalasta. Tapahtuma, joka on mahdoton sadassa vuodessa, voi olla väistämätön sadassa miljoonassa vuodessa."
– Carl Sagan
Onko sekunti lyhyt aika?
Myonin elinikä on noin \( 0{,}000\: 002 \) sekuntia
Silmänräpäys on noin \( 0{,}1 \) sekuntia
Vuorokaudessa on noin \( 86 \: 400 \) sekuntia.
Onko vuosikymmen pitkä aika?
Aurinko on \( 4 \: 600 \: 000 \: 000 \) vuotta vanha.
Peruskoulu kestää \( 9 \) vuotta.
Maailmankaikkeus on \( 13 \: 800 \: 000 \: 000 \) vuotta vanha.
Ajan suhteellisuus
Kymmenpotenssi
Isoja ja pieniä lukuja voidaan esittää kymmenenpotenssien avulla.
\( 10^{\color{purple}{2}}\color{black} \)
\( 10^{\color{purple}{3}}\color{black}\)
\( 10^{\color{purple}{-2}}\color{black} \)
\( 10^{\color{purple}{-3}}\color{black} \)
\( = 1\underbrace{\color{purple}{00}}_{2\text{ kpl}}\)
\( = 10\cdot 10 \)
\( = 10\cdot 10\cdot 10 \)
\( = 1\underbrace{\color{purple}{000}}_{3\text{ kpl}}\)
\( =\dfrac{1}{10^2}= \dfrac{1}{10\cdot 10}=\dfrac{1}{100} \)
\( = \underbrace{\color{purple}{0{,}0}}_{2\text{ kpl}}1\)
\(=\dfrac{1}{10^3}= \dfrac{1}{10\cdot 10\cdot 10}=\dfrac{1}{1000}\)
\( = \underbrace{\color{purple}{0{,}00}}_{3\text{ kpl}}1\)
Myonin elinikä \( 0{,}000\: 002 \) sekuntia voidaan kirjoittaa kymmenen potenssien avulla.
Maailmankaikkeuden ikä \( 13 \: 800 \: 000 \: 000 \) vuotta voidaan kirjoittaa kymmenen potenssien avulla.
Kymmenpotenssi
\( 13 \: \underbrace{800 \: 000 \: 000}_{9\text{ kpl}} \text{ a} \)
\( =13{,}8\cdot 10^9 \text{ a} \)
\( \underbrace{0{,} \: 000 \: 00}_{6\text{ kpl}}2 \text{ s} \)
\( =2\cdot 10^{-6} \text{ s} \)
Senttimetri, desimetri, ... mitä muita pituuden kerrannaisyksiköitä muistat?
mm
cm
dm
m
dam
hm
km
Pituuden kerrannaisyksiköitä
Pituuksien suhdeluku on 10
Kerrannaisyksiköt
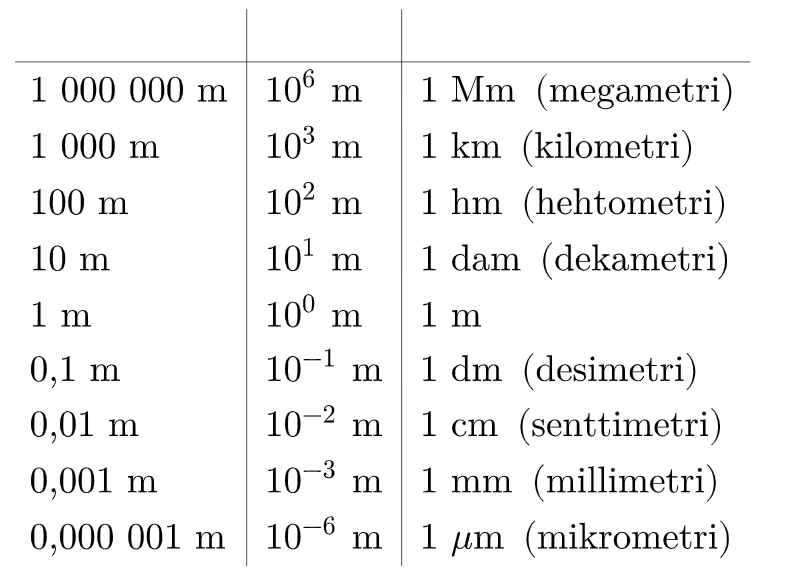
Suuruusluokka \( 1 \text{ dm}\) eli \( 10^{-1} \text{ m}\).
Suuruusluokka \( 1 \text{ mm}\) eli \( 10^{-3} \text{ m}\).
Suuruusluokka \( 1 \: \mu \text{m}\) eli \( 10^{-6} \text{ m}\).

Suuruusluokka \( 1 \: \text{nm}\) eli \( 10^{-9} \text{ m}\).
Suuruusluokka \( 10 \: \text{pm}\) eli \( 10\cdot 10^{-12} \text{ m}=10^{-11} \text{ m} \).
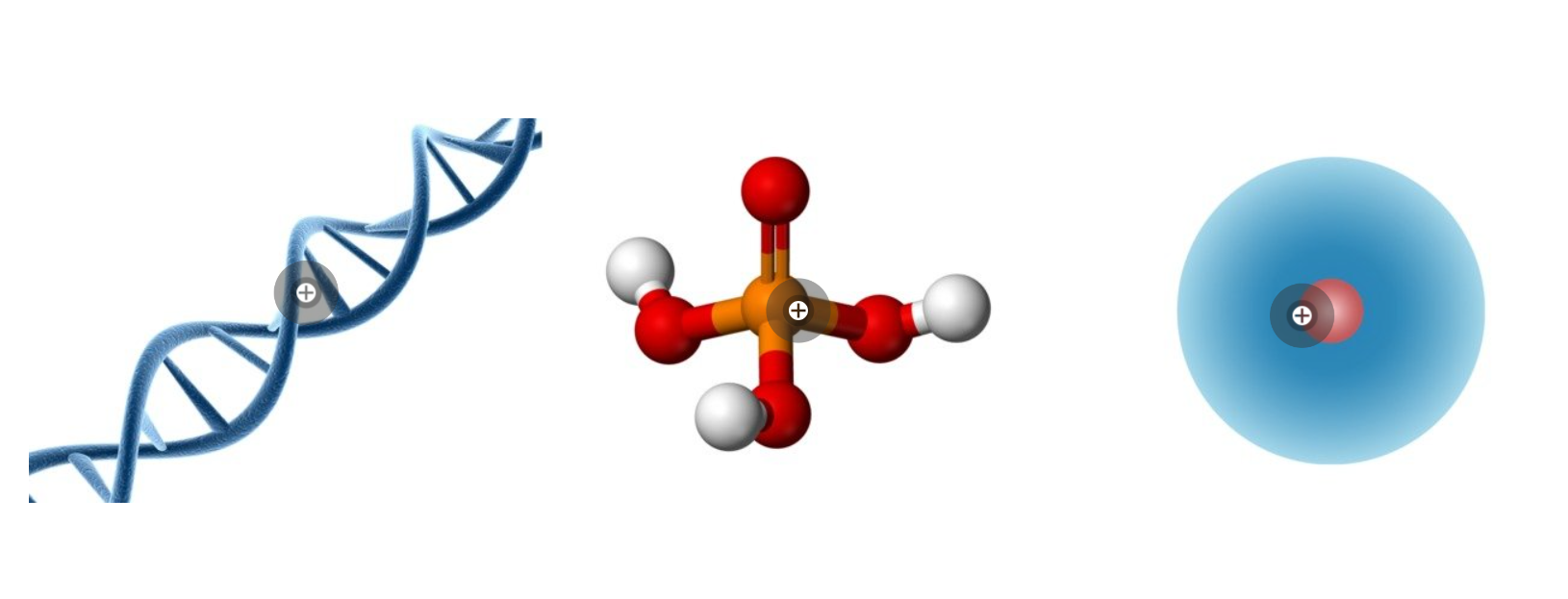
Suuruusluokka \( 10 \: \text{fm}\) eli \( 10\cdot 10^{-15} \text{ m}=10^{-14} \text{ m}\).
Suuruusluokka \( 10 \: \text{pm}\) eli \( 10\cdot 10^{-12} \text{ m}=10^{-11} \text{ m} \).
Suuruusluokka \( 1 \: \text{am}\) eli \( 10^{-18} \text{ m} \).
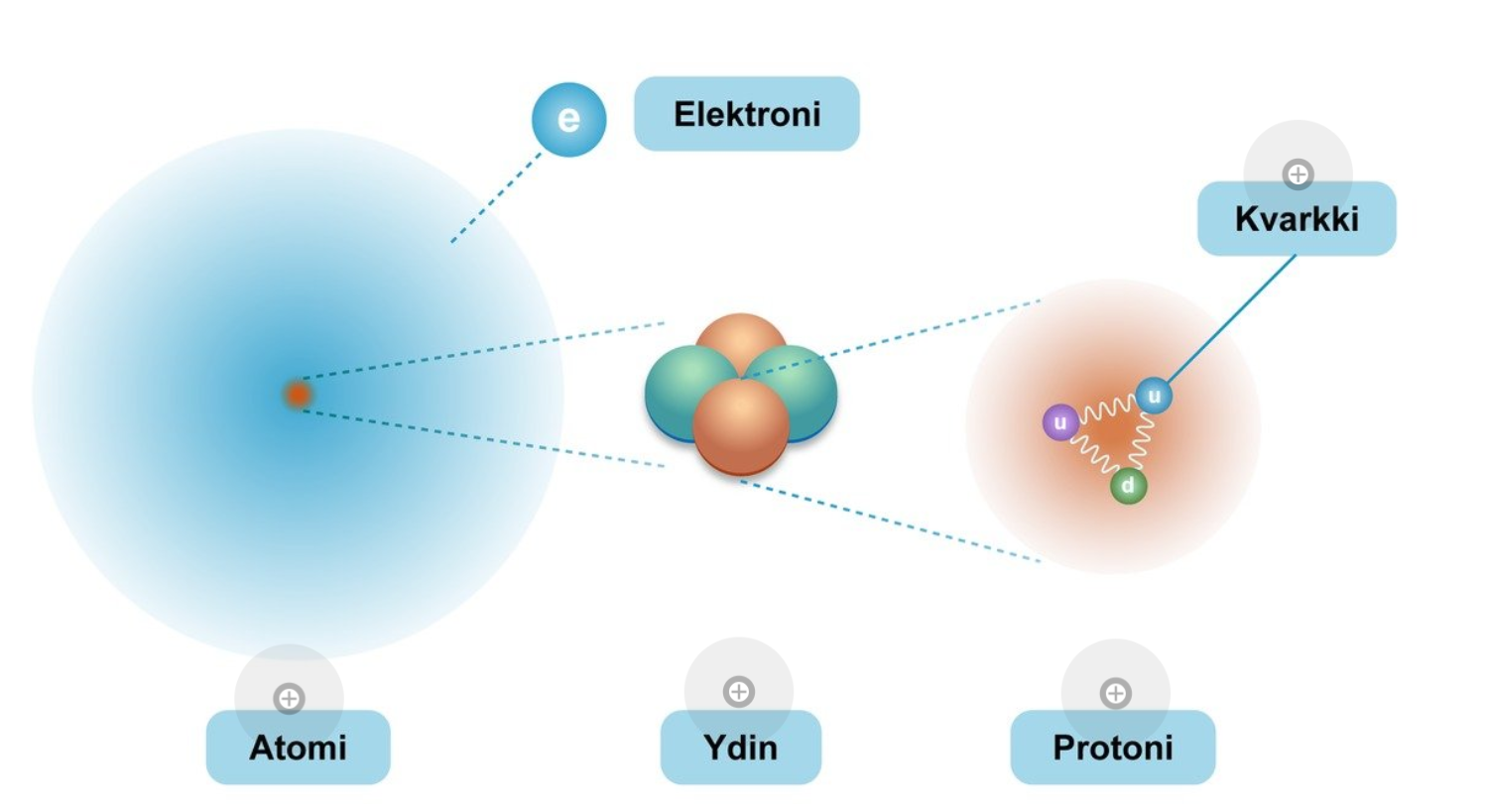
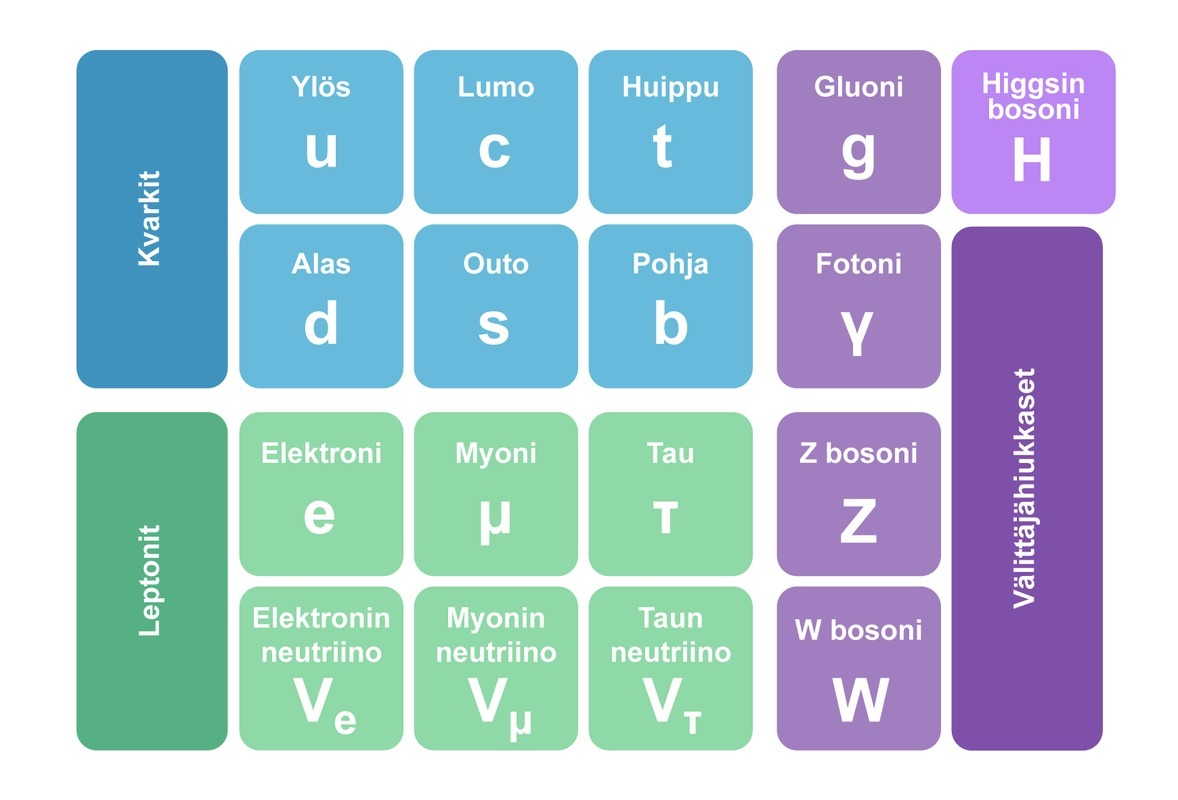
Hiukkasfysiikan standardimalli
- Miten esitetään hyvin pienet luvut käyttäen kymmenen potensseja?
- Mitä rakenteita havaitaan tarkasteltaessa ainetta yhä lähempää ja lähempää?
Pysähdy pohtimaan
Suureet ja maailmankaikkeuden kokoluokat
Maailmankaikkeuden suuret rakenteet
Suuruusluokka \( 1 \text{ m}\) eli \( 10^{0} \text{ m}\).
Suuruusluokka \( 1 \text{ dam}\) eli \( 10^{1} \text{ m}\).
Suuruusluokka \( 1 \text{ km}\) eli \( 10^{3} \text{ m}\).

Maan halkaisijan suuruusluokka on \( 10 \: 000 \: 000 \text{ m}\) eli \( 10\cdot \color{purple}{10^{6}} \color{black}\text{ m}\) eli \( 10 \text{ \color{purple}{M}\color{black}m}\).
Jupiterin halkaisijan suuruusluokka on \( 100 \: 000 \: 000 \text{ m}\) eli \(100\cdot \color{purple}{10^{6}} \color{black}\text{ m}\) eli \( 100 \text{ \color{purple}{M}\color{black}m}\).
Auringon halkaisijan suuruusluokka on \( 1 \: 000 \: 000 \: 000 \text{ m}\) eli \( \color{purple}{10^{9}} \color{black}\text{ m}\) eli \( 1 \text{ \color{purple}{G}\color{black}m}\).



\( 150 \: 000 \: 000 \: \color{purple}{000}\color{black} \text{ m} \)
\( =150 \: 000 \: 000 \text{\color{purple}{k}\color{black}m} \)
Maapallon etäisyys Auringosta on yksi tähtiteteellinn yksikkö eli \( 1 \text{ AU}\).
Valo matkustaa Auringosta Maapallolle noin 8 minuuttia.
Maapallo ja Aurinko
Aurinkokunnan halkaisija on noin \( 300 \: 000 \: 000 \: 000 \: 000 \text{ m}\) eli \( 0{,}3\cdot 10^{15} \text{ m} \) eli \( 0{,}3 \text{ Pm}\).
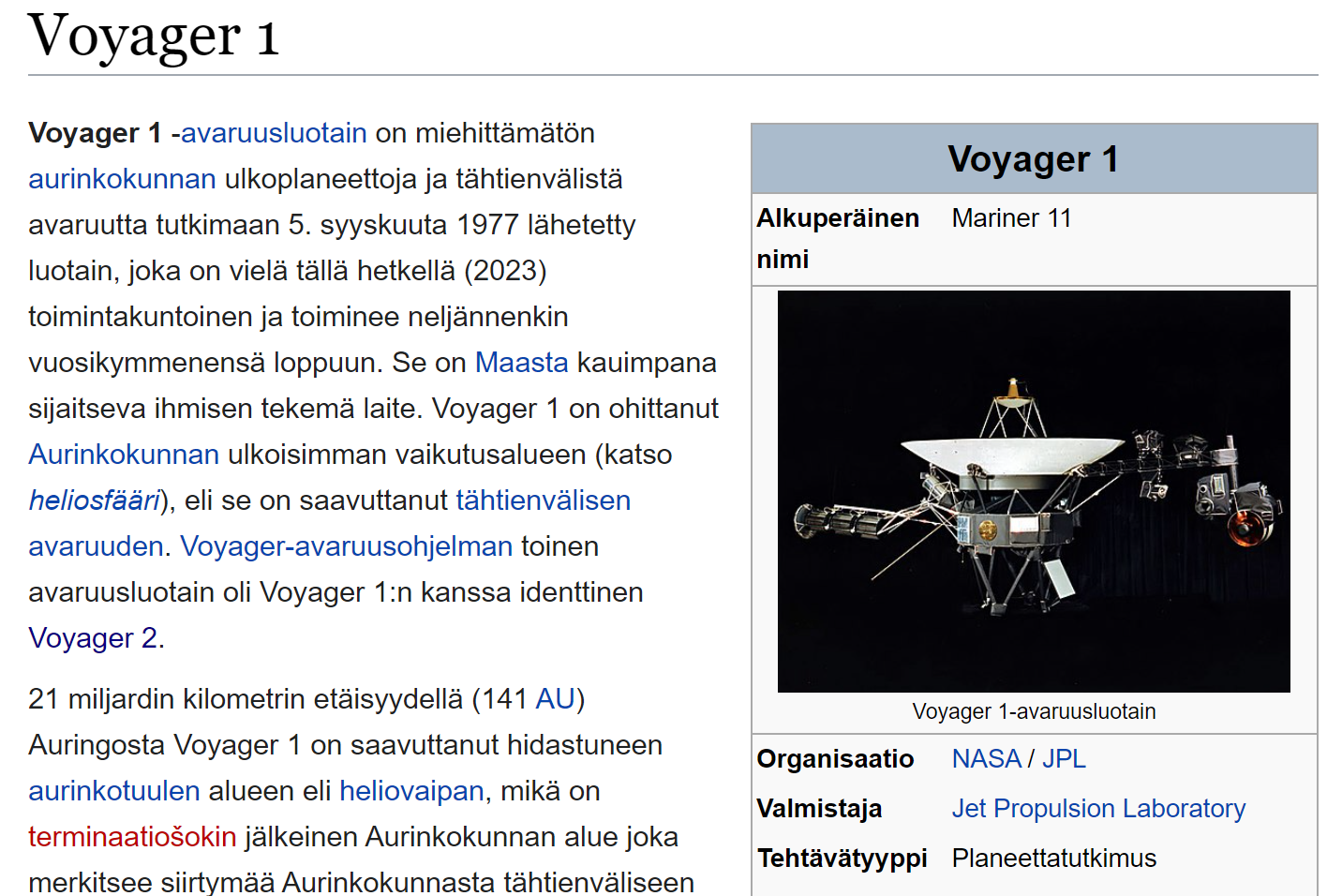
Esimerkki

Esimerkki
Kuinka kauan kestää lähettää käsky Voyager 1 luotaimelle, kun luotaimen etäisyys Maapallosta on 141 AU?
Pohdintaa
Mitä tietoja tarvitset?
Miten lasket ajan?
Voyager 1 luotaimen ottama kuva Maapallosta noin 6 miljardin kilometrin päästä.
Esimerkki
Atomin ytimen läpimitta 2,0 fm.
Ilmoita seuraavat arvot kymmenpotenssien avulla.
a)
b)
Pienen solun läpimitta 70 nm.
c)
Kovalevyn tilaisuus 2,0 Tb
d)
Yhtä voipakettia vastaava energiamäärä 38 MJ.
Ratkaisu
a)
b)
c)
d)
Esimerkki
Ilmoita seuraavat arvot kymmenpotenssien ja kerrannaisyksiköiden avulla.
a) Keskietäisyys Maasta Aurinkoon 14 960 000 000 m
b) Hiuksen paksuus 0,000 05 m
Ratkaisu
a) Keskimääräinen etäisyys Maasta Aurinkoon:
14 960 000 000 m
= 14 960 000 km
= 14,96 \( \cdot \) 1 000 000 km
= 14,96 \( \cdot 10^6\) km
b) Hiuksen paksuus:
0,000 05 m
= 0,005 cm
= 0,05 mm
= 5 \( \cdot \) 0,01 mm
= 5 \( \cdot 10^{-2}\) mm
|| 1000 m = 1 km
|| 0,01 m = 1 cm
|| 0,1 cm = 1 mm
- Miten esitetään suuret luvut käyttäen kymmenen potensseja?
- Miten kymmenen potenssien tilalla voidaan käyttää myös kerrannaisyksiköitä?
Pysähdy pohtimaan
Suureet ja maailmankaikkeuden kokoluokat
Mittaaminen ja suureet
Pohdi...
Mitä voidaan mitata?
Mitä ei voida mitata?

Mittaaminen
Miten muinaiset kansat jaksottivat aikaa?
Mihin aurinkokellon toiminta perustuu?

Miten pituuksia mitattiin?
Kvantifiointi
Kvantifioinnissa siirrytään asian laadullisesta eli kvalitatiivisesta kuvailusta ("vettä on paljon") määrälliseen eli kvantitatiiviseen kuvailuun ("vettä on 129 litraa").











Suure
Ympäröivää maailmaa voi kuvata esimerkiksi suureiden avulla.

Suure on ilmiön, kappaleen tai aineen mitattavissa oleva ominaisuus.



Mitä eroa on suureilla nopeus ja
Fysiikan suurejärjestelmä
massa?


"vauhtimittari"
vaaka
Suure, jolla on sekä suuruus että suunta
Esim.
Vektorisuure
nopeus, voima, kiihtyvyys
Suure, jolla on pelkkä suuruus
Skalaarisuure
Esim.
massa, pituus, lämpötila
Suureen mittaaminen
Suureita mitataan vertaamalla niitä sovittuun mittayksikköön.

Esim.
1,0 kg tai 1,0 m
massan mittayksikkö 1,0 kg sisältyy mitattuun massaan.
Kappaleen massaa selvittäessä on mitattava, kuinka monta kertaa


Système international d’unités
(SI-järjestelmä)
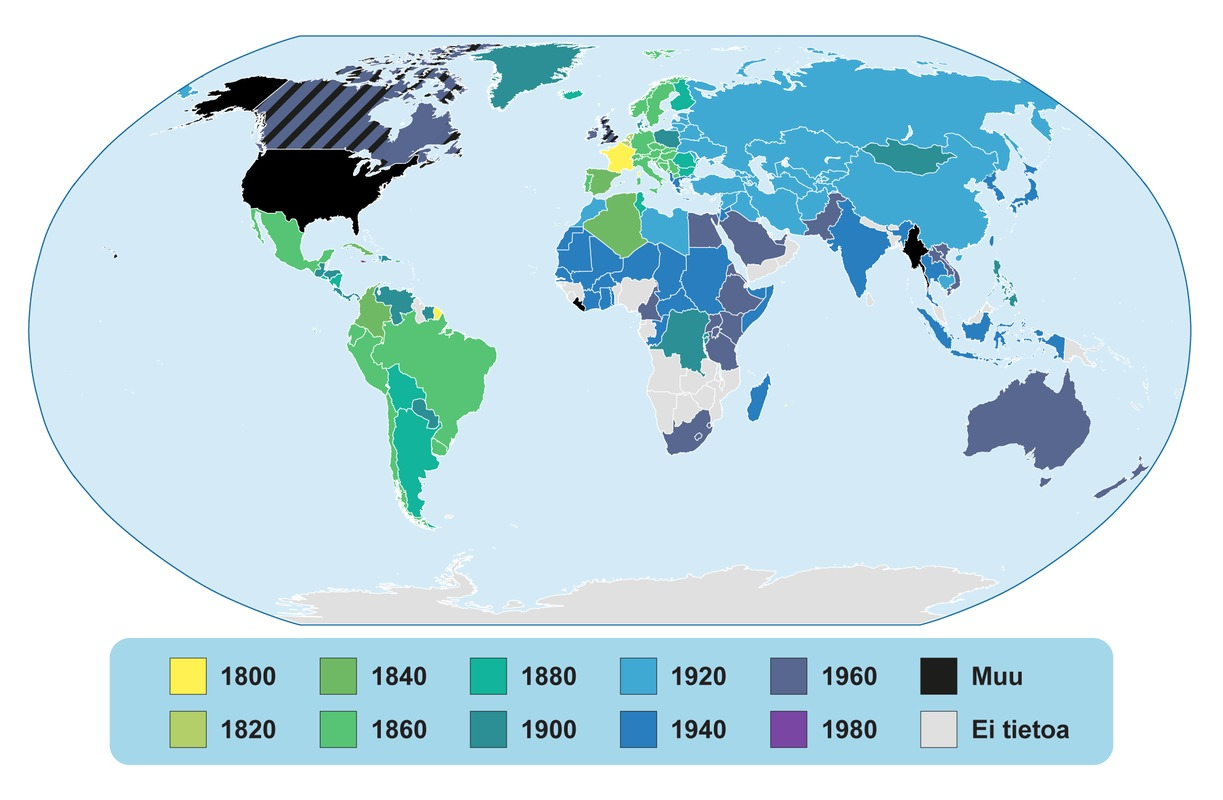
SI-järjestelmä sai nimensä 1960-luvulla.
SI-järjestelmä perustuu jo 1700-luvun lopulla käyttöön otettuun metrijärjestelmään.
Suomessa otettiin käyttöön metrijärjestelmä vuonna 1892 ja SI-järjestelmä vuonna 1975.
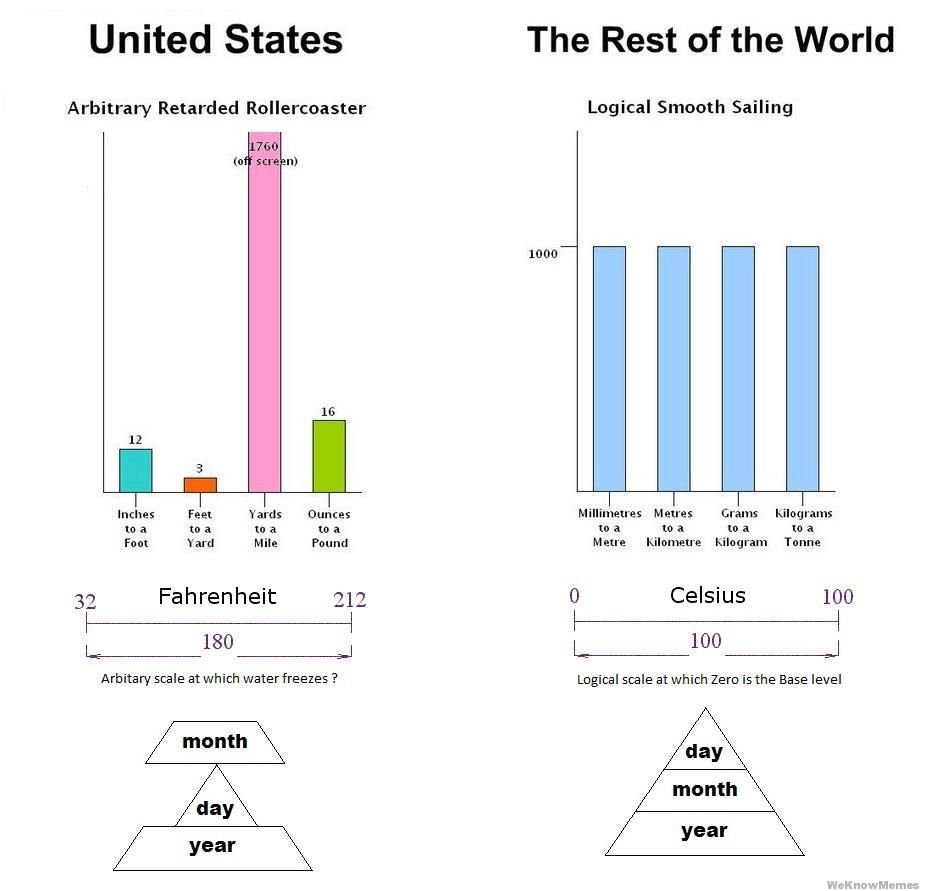
Système international d’unités
Perussuureet
suure
suureen tunnus
yksikkö
yksikön tunnus
pituus
massa
aika
sähkövirta
lämpötila
ainemäärä
valovoima
l, s tai x
m
t
I
T
n
I
metri
sekunti
kilogramma
ampeeri
kelvin
mooli
kandela
m
kg
s
A
K
mol
cd
Esimerkkejä johdannaissuureista
Nopeus
Kiihtyvyys
Perussuureiden avulla määritellään kaikki muut SI-järjestelmän suureet.
- Mitä ovat suureet ja yksiköt?
- Mitä tarkoittaa kvantifiointi?
- Miksi on hyödyllistä, että kaikissa maissa käytetään samoja mittayksiköitä?