3 Mittaaminen

Keskeiset käsitteet:

karkea mittausvirhe

satunnainen mittausvirhe

systemaattinen mittausvirhe

virherajat

suure

yksikkö

merkitsevä numero

Suure

Ympäröivää maailmaa voi kuvata esimerkiksi suureiden avulla.

Suure on ilmiön, kappaleen tai aineen mitattavissa oleva ominaisuus.

Suureen mittaaminen

Suureita mitataan vertaamalla niitä sovittuun mittayksikköön.

CC BY-SA 3.0 Uploaded by Greg A L

Esim. 

1,0 kg tai 1,0 m

massan mittausyksikköä 1,0 kg sisältyy mitattuun massaan.

3,0
1,0 \text{ kg}
= 3,0 \text{ kg}

Kappaleen massaa selvittäessä on mitattava, kuinka monta kertaa 

\cdot
m=

lähde

Mittausvirheet

Vesilasissa on jääpaloja ja vettä.

Mihin lämpötilaan vesi ja jääpalat asettuvat? 

\( \rightarrow \ 0^\circ\text{C} \)

Vesilasiin laitetaan lämpömittari, joka mittaa seoksen lämpötilaksi \( 0{,}8\ ^\circ \text{C}\).

Mittaus toistetaan, mutta joka kerta sama lämpömittari näyttää seoksen lämpötilaksi liian suuren lukeman, \( 0{,}8\ ^\circ \text{C}\).

Miten lämpömittarin systemaattinen virhe voidaan ottaa huomioon?

\( \rightarrow \) Mittaustarkkuutta voidaan parantaa vähentämällä lämpömittarin lukemasta \( 0{,}8\ ^\circ \text{C}\).

Mittausvirheet

Pallo pudotetaan pöydältä lattialle ja putoamisaika mitataan sekuntikellolla.

Jokaisessa mittaustuloksessa esiintyy satunnainen virhe, joka johtuu sekuntikellon käynnistämisestä ja pysäyttämisestä.

\( \rightarrow \) Mittaustarkkuutta voidaan parantaa pudottamalla pallo useita kertoja ja laskemalla putoamisaikojen keskiarvo. 

Miten putoamisajan mittaustulosta voidaan parantaa?

Mittausvirheet

Kolme henkilöä mittaa sadan metrin juoksuaikaa sekuntikellolla.

Yhden ajanottajan huomio herpaantuu lähtöhetkellä, ja hän käynnistää mittauksen selvästi myöhässä.

\( \rightarrow \) Hylätään herpaantuneen mittaajan mittaustulos karkeana virheenä ja lasketaan kahden muun mittaajan aikojen keskiarvo. 

Miten juoksuajan mittaustulos kannattaa ilmoittaa?

Mittalaitteen tarkkuus ja virheen ilmoittaminen

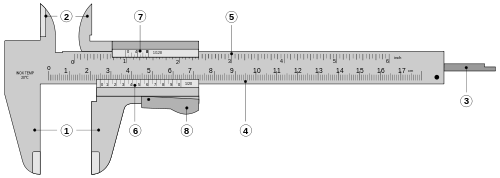
Viivoitin

Mittaustulos:

65 mm

Työntömitta

Mittaustulos: 

65,3 mm

Mittaustuloksen yhteydessä ilmoitetaan usein tarkkuus.

Tarkkuus: 1 mm

Tarkkuus: 0,1 mm

Mittaustuloksen ilmoittaminen

Viivoitin

Mittaustulos:

65 mm

Työntömitta

Mittaustulos: 

65,3 mm

Joaquim Alves Gaspar CC BY SA 3.0

Tarkkuus: 1 mm

Tarkkuus: 0,1 mm

x=x_m\pm \Delta x,

jossa \( x \) on mitattu suure, \( x_m \) on mittaustulos ja \( \Delta x \) on virhe, joka on vähintään mittalaitteen tarkkuus.

x=65 \text{ mm} \pm 1 \text{ mm}
x=65,3 \text{ mm} \pm 0,1 \text{ mm}
Aika (s) Poikkeama (s)
0,39 0,003
0,42 0,033
0,36 0,017
0,38 0,007
0,39 0,003
0,43 0,043
0,34 0,047
Keskiarvo 0,387 0,022

Pudotetaan pallo samalta korkeudelta seitsemän kertaa. Mitataan putoamiseen kuluva aika. 

Virheen arviointi toistomittauksessa

\begin{aligned}&\vert 0{,}39 \text{ s } - 0{,}387 \text{ s}\vert \\ &=0{,}003 \text{ s} \end{aligned}

 | Mittaustulos - Keskiarvo |

\( \rightarrow \) Virheen suuruusluokka on sadasosasekuntteja, joten putoamisaika on \( t=0{,}39 \text{ s } \pm 0{,}02 \text{ s} \).

Merkitsevät numerot

Kokonaisluvun lopussa olevat nollat eivät ole merkitseviä numeroita.

1200 g 

150 cm 

20 m/s

900 N

1, 2

1, 5

2

9

Desimaaliluvun alussa olevat nollat eivät ole merkitseviä numeroita.

0,010 kg

0,18 km 

0,55 m/s

0,6 N

1, 0

1, 8

5, 5

6

Kaikki muut numerot ovat merkitseviä numeroita.

Suuren arvon ilmoittamiseen sisältyy aina sen tarkkuuden ilmaisu.

Esimerkiksi jos puhelimen paksuus on 7,8 mm, niin puhelimen paksuus on mitattu millimetrin kymmenesosan tarkkuudella ja merkitseviä numeroita on 2.

Merkitsevät numerot laskuissa

Sahataan 1 metrin pituinen lauta kolmeen osaan, jolloin yhden osan pituus on \( \frac{1 \text{ m}}{3}=0,33\ldots \text{ m} \).

Millä tarkkuudella tulos annetaan?

  • Jos 1 m, niin yhden osan pituus on 0,3 m
  • Jos 1,0 m, niin yhden osan pituus o 0,33 m
  • Jos 1,00 m, niin yhden osan pituus on 0,333 m

Vastauksessa sama määrä merkitseviä numeroita kuin epätarkimmassa lähtöarvossa.

  • Mitattavia ominaisuuksia kutsutaan suureiksi.
  • Suureen arvo koostuu lukuarvosta ja mittayksiköstä.
  • Mittaustulokset ovat aina likiarvoja. Merkitsevät numerot kuvaavat mittaustuloksen tarkkuutta.
  • Luvussa merkitseviä numeroita ovat kaikki muut paitsi kokonaislukujen loppussa olevat nollat ja desimaalilukujen alussa olevat nollat.

Yhteenvetoa