Mittaaminen ja graafinen esitys

Mittaaminen fysiikassa

Mittausvirheet

Vesilasissa on jääpaloja ja vettä.

Mihin lämpötilaan vesi ja jääpalat asettuvat?

\( \rightarrow \ 0^\circ\text{C} \)

Vesilasiin laitetaan lämpömittari, joka mittaa seoksen lämpötilaksi \( 0{,}8\ ^\circ \text{C}\).

Mittaus toistetaan, mutta joka kerta sama lämpömittari näyttää seoksen lämpötilaksi liian suuren lukeman, \( 0{,}8\ ^\circ \text{C}\).

Miten lämpömittarin systemaattinen virhe voidaan ottaa huomioon?

\( \rightarrow \) Mittaustarkkuutta voidaan parantaa vähentämällä lämpömittarin lukemasta \( 0{,}8\ ^\circ \text{C}\).

Mittausvirheet

Pallo pudotetaan pöydältä lattialle ja putoamisaika mitataan sekuntikellolla.

Jokaisessa mittaustuloksessa esiintyy satunnainen virhe, joka johtuu sekuntikellon käynnistämisestä ja pysäyttämisestä.

\( \rightarrow \) Mittaustarkkuutta voidaan parantaa pudottamalla pallo useita kertoja ja laskemalla putoamisaikojen keskiarvo.

Miten putoamisajan mittaustulosta voidaan parantaa?

Mittausvirheet

Kolme henkilöä mittaa sadan metrin juoksuaikaa sekuntikellolla.

Yhden ajanottajan huomio herpaantuu lähtöhetkellä, ja hän käynnistää mittauksen selvästi myöhässä.

\( \rightarrow \) Hylätään herpaantuneen mittaajan mittaustulos karkeana virheenä ja lasketaan kahden muun mittaajan aikojen keskiarvo.

Miten juoksuajan mittaustulos kannattaa ilmoittaa?

Mittalaitteen tarkkuus ja virheen ilmoittaminen

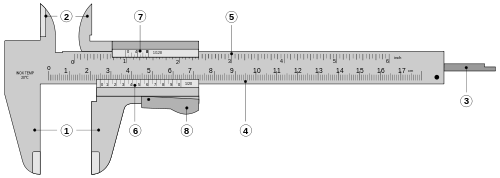
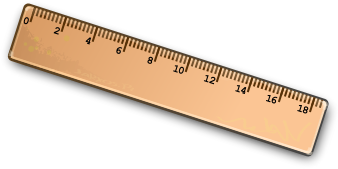
Viivoitin

Mittaustulos:

65 mm

Työntömitta

Mittaustulos:

65,3 mm

Mittaustuloksen yhteydessä ilmoitetaan usein tarkkuus.

Tarkkuus: 1 mm

Tarkkuus: 0,1 mm

Mittaustuloksen ilmoittaminen

Viivoitin

Mittaustulos:

65 mm

Työntömitta

Mittaustulos:

65,3 mm

Joaquim Alves Gaspar CC BY SA 3.0

Tarkkuus: 1 mm

Tarkkuus: 0,1 mm

x=x_m\pm \Delta x,

jossa \( x \) on mitattu suure, \( x_m \) on mittaustulos ja \( \Delta x \) on virhe, joka on vähintään mittalaitteen tarkkuus.

x=65 \text{ mm} \pm 1 \text{ mm}

x=65,3 \text{ mm} \pm 0,1 \text{ mm}

	Aika (s)	Poikkeama (s)
	0,39	0,003
	0,42	0,033
	0,36	0,017
	0,38	0,007
	0,39	0,003
	0,43	0,043
	0,34	0,047
Keskiarvo	0,387	0,022

Pudotetaan pallo samalta korkeudelta seitsemän kertaa. Mitataan putoamiseen kuluva aika.

Virheen arviointi toistomittauksessa

\begin{aligned}&\vert 0{,}39 \text{ s } - 0{,}387 \text{ s}\vert \\ &=0{,}003 \text{ s} \end{aligned}

| Mittaustulos - Keskiarvo |

\( \rightarrow \) Virheen suuruusluokka on sadasosasekuntteja, joten putoamisaika on \( t=0{,}39 \text{ s } \pm 0{,}02 \text{ s} \).

Merkitsevät numerot

Kokonaisluvun lopussa olevat nollat eivät ole merkitseviä numeroita.

1200 g

150 cm

20 m/s

900 N

1, 2

1, 5

Desimaaliluvun alussa olevat nollat eivät ole merkitseviä numeroita.

0,010 kg

0,18 km

0,55 m/s

0,6 N

1, 0

1, 8

5, 5

Kaikki muut numerot ovat merkitseviä numeroita.

Suuren arvon ilmoittamiseen sisältyy aina sen tarkkuuden ilmaisu.

Esimerkiksi jos puhelimen paksuus on 7,8 mm, niin puhelimen paksuus on mitattu millimetrin kymmenesosan tarkkuudella ja merkitseviä numeroita on 2.

Merkitsevät numerot laskuissa

Sahataan 1 metrin pituinen lauta kolmeen osaan, jolloin yhden osan pituus on \( \frac{1 \text{ m}}{3}=0,33\ldots \text{ m} \).

Millä tarkkuudella tulos annetaan?

Jos 1 m, niin yhden osan pituus on 0,3 m
Jos 1,0 m, niin yhden osan pituus o 0,33 m
Jos 1,00 m, niin yhden osan pituus on 0,333 m

Vastauksessa sama määrä merkitseviä numeroita kuin epätarkimmassa lähtöarvossa.

Millaisia erityyppisiä virheitä mittaukseen voi sisältyä?
Miten ilmaistaan mittauksen tulos virherajoineen?
Miten arvioidaan virheen suuruus toistomittauksessa?
Mitä ovat merkitsevät numerot, ja miten määräytyy laskutoimitusten vastausten tarkkuus?

Pysähdy pohtimaan

Graafinen malli

Mittaaminen ja graafinen esitys

Lineaarinen malli

Mallintaminen

Mittaustulosten pohjalta laaditaan malleja, joiden tarkoitus on selittää luonnossa havaittuja ilmiöitä.

Matemaattisten mallien avulla voidaan tehdä ennustuksia.

Malli on aina yksinkertaistus, approksimaatio, todellisuudesta jolla on oma pätevyysalue.

Mallintaminen

Heilurin pituuden ja heilahdusajan välisen riippuvuuden graafinen malli

Heilurin pituuden ja heilahdusajan välisen riippuvuuden matemaattinen malli

T=2\pi\sqrt{ \dfrac{l}{g}}

Mallintaminen

Heilurin pituuden ja heilahdusajan välisen riippuvuuden graafinen malli

Heilurin pituuden ja heilahdusajan välisen riippuvuuden matemaattinen malli

T=2\pi\sqrt{ \dfrac{l}{g}}

Mallit

Fysiikassa malleille kuvataan tutkittavia kohteita.

Säämalleilla voidaan ennustaa säätilan kehittymistä

Atomimallin avulla voidaan kuvata atomin rakennetta.

Mallit ovat aina yksinkertaistuksia luonnon monimutkaisista tapahtumista ja ilmiöistä.

Mallit laaditaan tutkimustiedon ja tunnetun tiedon varaan.

Mallien avulla voidaan selittää havaintoja ja tehdä ennusteita.

Graafinen malli

Malli voi olla esimerkiksi koordinaatistoon piirretty kuvaaja, joka kuvaa kahden suureen välistä riippuvuutta.

Tutkitaan raudan ja alumiinin massan riippuvuutta sen tilavuudesta.

Esimerkki

Sijoitetaan mittaustulokset
(V, m) -koordinaatistoon

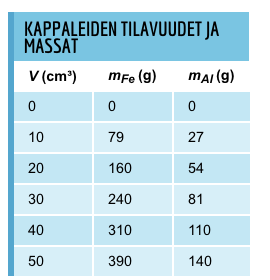
Graafinen malli

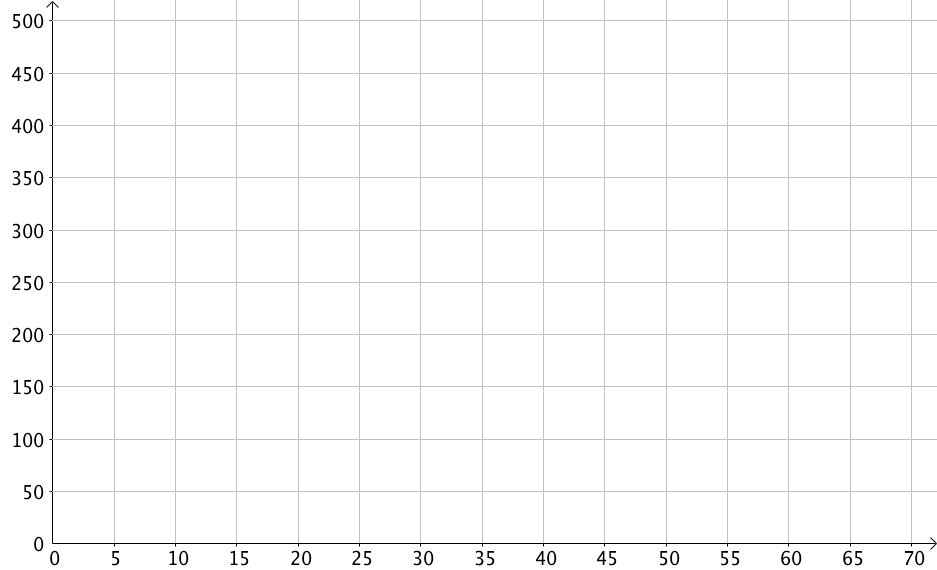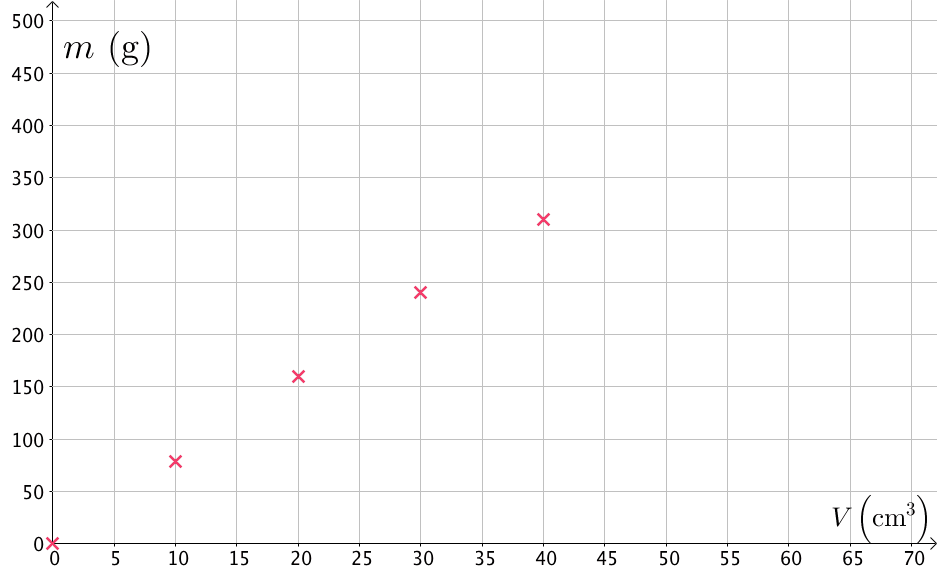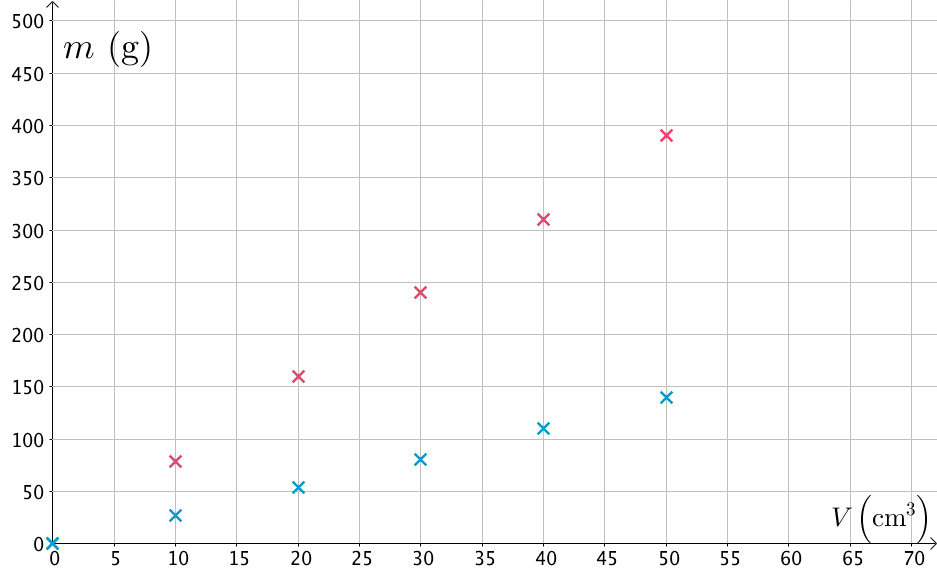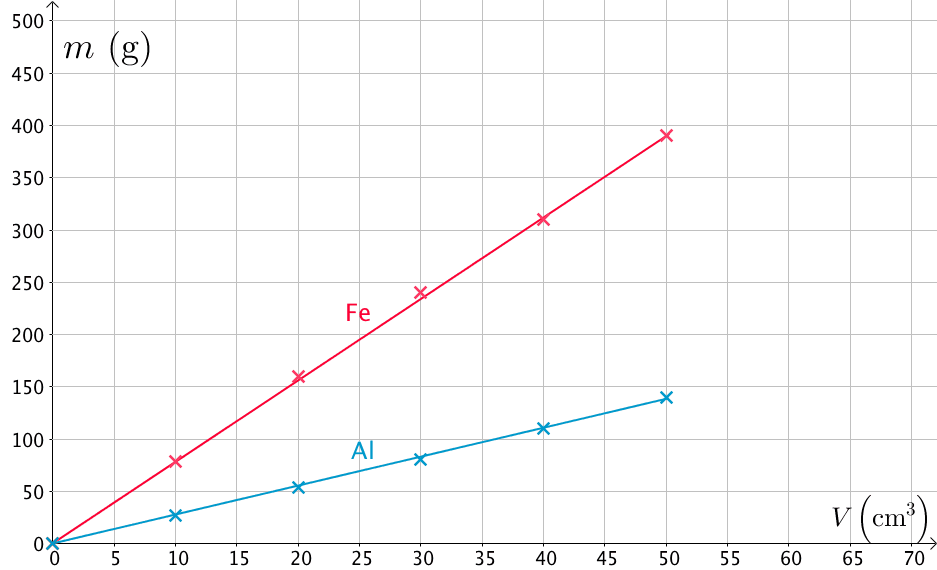
Pistejoukkoon sovitetaan suora, joka kulkee mahdollisimman hyvin pistejoukon keskeltä.

Tätä menetelmää kutsutaan graafiseksi tasoitukseksi.

Tiheyden määrittäminen

\rho_\text{Fe}=\dfrac{\Delta m}{\Delta V}=\dfrac{350 \text{ g}}{45 \text{ cm}^3}\approx 7,8 \text{ g/cm}^3

\rho = \frac{m}{V}

[\rho]=\dfrac{1 \text{ kg}}{1 \text{ m}^3}=1 \text{ kg/m}^3

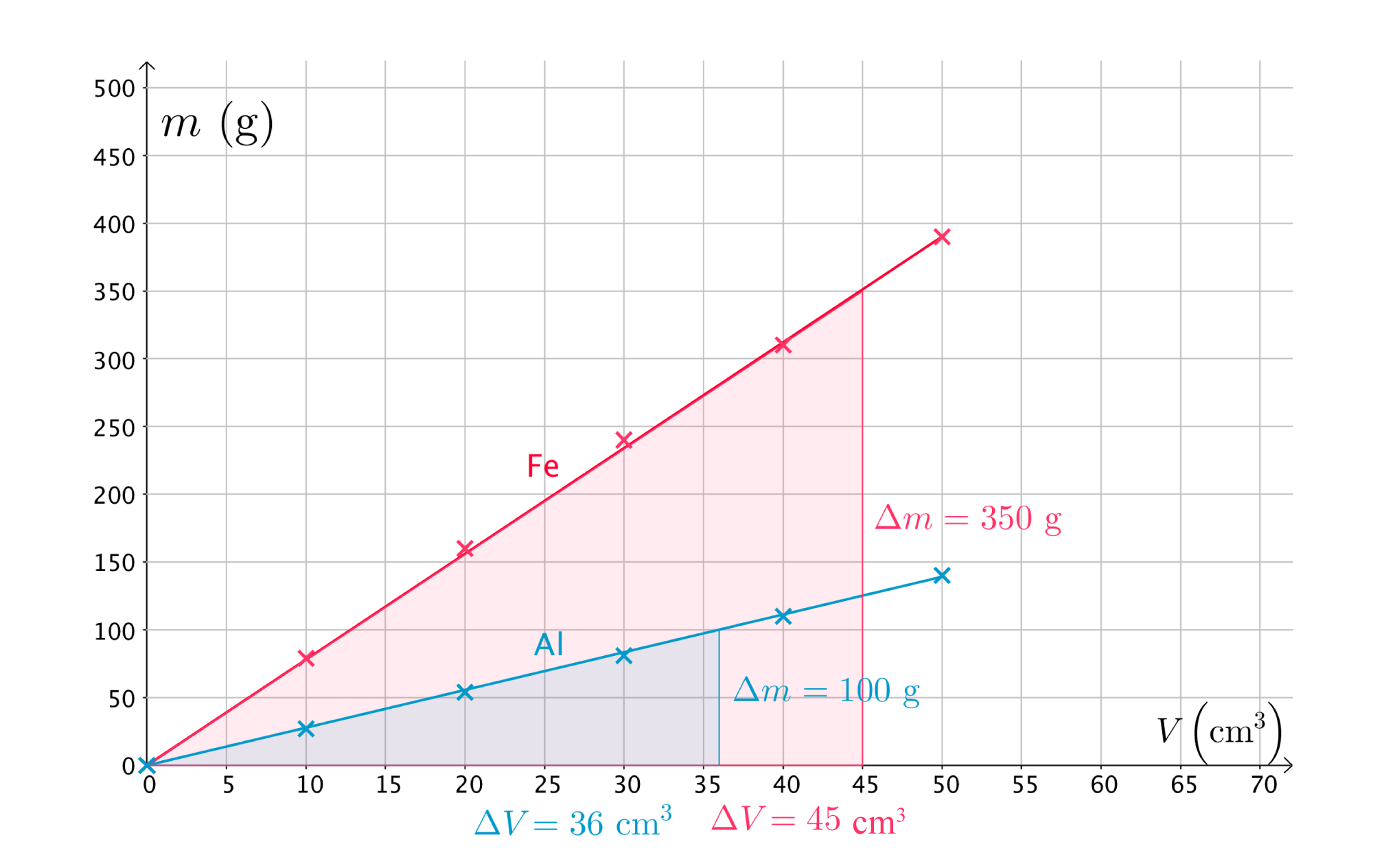
Tiheys

Interpolointi ja ekstrapolointi

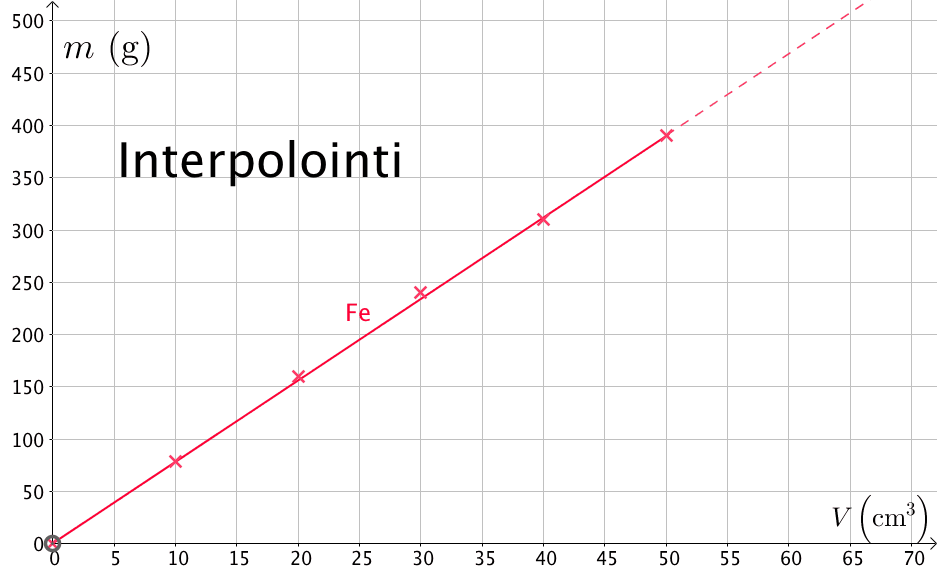
Lineaariset ja epälineaariset mallit

Esimerkki

Pekka tutki kahvin jäähtymistä emalimukissa. Hän kaatoi kahvia mukiin, mittasi kahvin lämpötilan minuutin välein ja kirjasi tulokset tietokoneelle.

Pekan mittaussarjan tulokset on annettu taulukossa 2.A. Aineisto: 2.A Taulukko: Kahvin jäähtyminen

Laadi valitsemallasi ohjelmalla mittaussarjan tuloksista kahvin lämpötilan kuvaaja ajan funktiona ja liitä kuvaaja kuvakaappauksena vastauslaatikkoon. (S2018/T2, muokattu)

Mitä tarkoitetaan mallilla?
Miten muodostetaan graafinen malli suureiden välisestä riippuvuudesta?
Miten tehdään ennusteita graafisen mallin perusteella?
Miten suoraan verrannolliset suureet suhtautuvat toisiinsa?