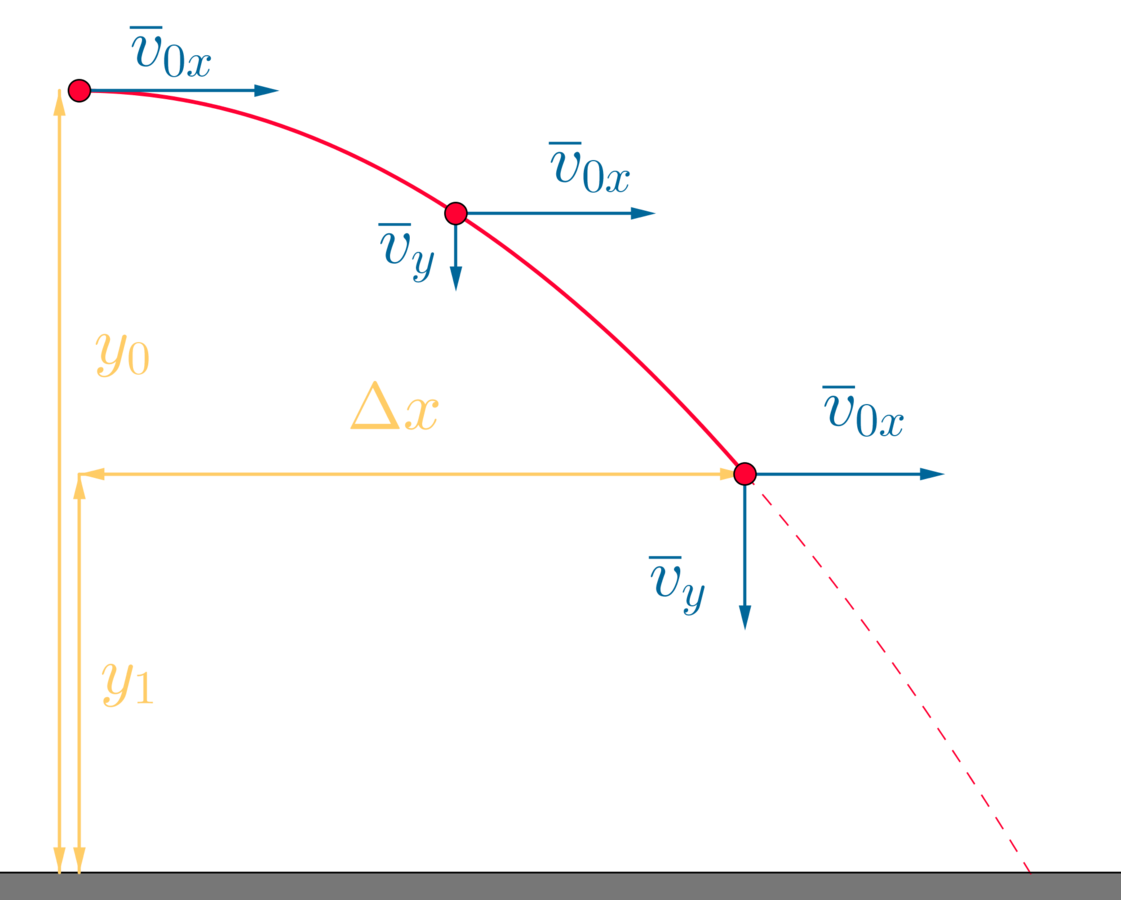
Vaakasuora heittoliike

Oletetaan, että palloihin vaikuttava ilmanvastus on mitätön.

Vihreä ja punainen pallo ovat samalla korkeudella jokaisella ajanhetkellä.

Vihreä pallo pudotetaan ja punainen pallo heitetään vaakasuoraan samalla hetkellä samalta korkeudelta.

Vaakasuora heittoliike

Molempiin palloihin vaikuttaa ainoastaan paino G, joka vaikuttaa pystysuunnassa.

Pallojen liike pystysuunnassa on tasaisesti kiihtyvää.

Vaakasuunnassa palloihin ei vaikuta voimia.

Pallojen liike vaakasuunnassa on tasaista. 

Pallon liike vaakasuunnassa on tasaista, joten sen nopeus vaakasuunnassa ei muutu.

x(t)=\color{CornflowerBlue}{v_{0x}} t
x(t)=v0xtx(t)=\color{CornflowerBlue}{v_{0x}} t

Vaakasuora heittoliike

Pallon x-akselin suuntainen paikka ajan funktiona

v_x(t)=\color{CornflowerBlue}{v_{0x} }
vx(t)=v0xv_x(t)=\color{CornflowerBlue}{v_{0x} }

Pallon x-akselin suuntainen nopeus ajan funktiona

Pallon liike pystysuunnassa on tasaisesti kiihtyvää.

Vaakasuora heittoliike

Pallon y-akselin suuntainen nopeus ajan funktiona

v_y(t)=-\color{Goldenrod}{a_y}t
vy(t)=−aytv_y(t)=-\color{Goldenrod}{a_y}t
=-\color{Goldenrod}{g}t
=−gt=-\color{Goldenrod}{g}t

Pallon y-akselin suuntainen paikka ajan funktiona

y(t)=y_0-\dfrac{1}{2}\color{Goldenrod}gt^2
y(t)=y0−12gt2y(t)=y_0-\dfrac{1}{2}\color{Goldenrod}gt^2

Vaakasuora heittoliike

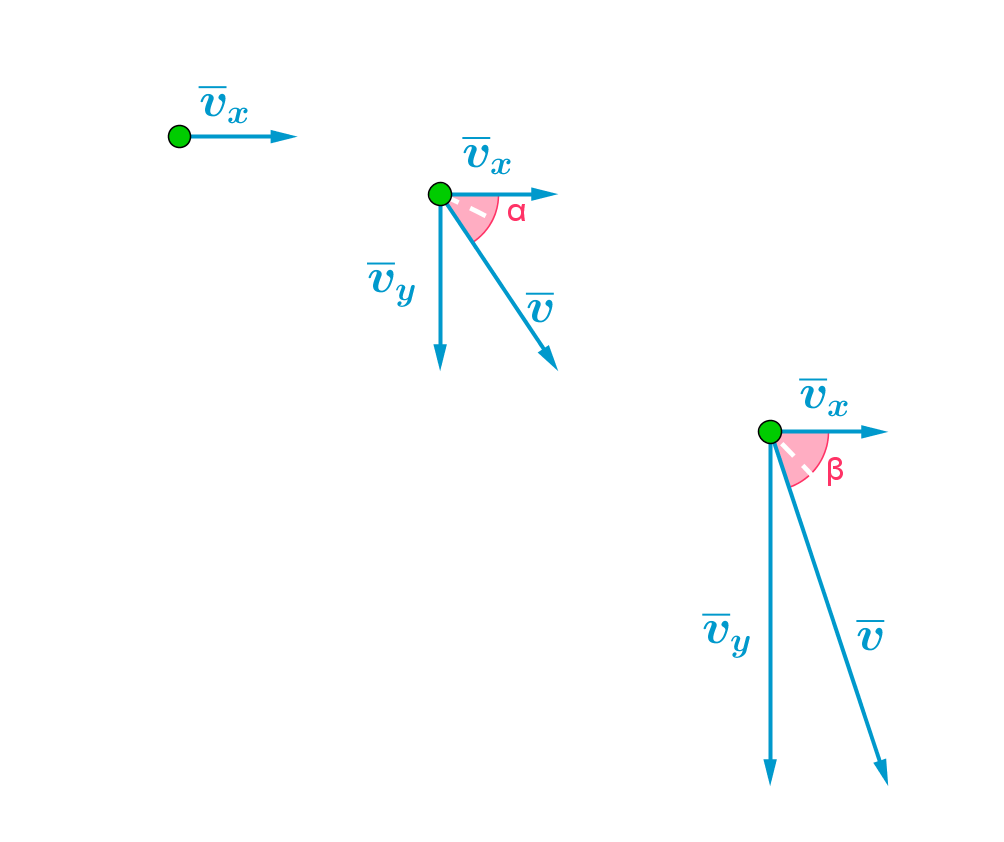
Nopeus hetkellä t saadaan laskettua vektorisummana. 

\color{CornflowerBlue}{\overline{v}}=\color{CornflowerBlue}{\overline{v}_x}+\color{CornflowerBlue}{\overline{v}_y}
v‾=v‾x+v‾y\color{CornflowerBlue}{\overline{v}}=\color{CornflowerBlue}{\overline{v}_x}+\color{CornflowerBlue}{\overline{v}_y}

Nopeuden suuruus saadaan Pythagoraan lauseen avulla.

\color{CornflowerBlue}{v}=\sqrt{\color{CornflowerBlue}{v_x}^2+\color{CornflowerBlue}{v_y}^2}
v=vx2+vy2\color{CornflowerBlue}{v}=\sqrt{\color{CornflowerBlue}{v_x}^2+\color{CornflowerBlue}{v_y}^2}

Nopeuden suunta saadaan tangentin avulla.

\tan \alpha = \dfrac{\color{CornflowerBlue}{v_y}}{\color{CornflowerBlue}{v_x}}
tanα=vyvx\tan \alpha = \dfrac{\color{CornflowerBlue}{v_y}}{\color{CornflowerBlue}{v_x}}

Esimerkki

Laskuvarjohyppääjä hyppää 4 000 metristä lentokoneesta, joka etenee nopeudella 400 km/h maanpinnan suhteen. 

Kuinka kauan kestää, että hyppääjä putoaa 1 500 metrin korkeuteen, jossa hän avaa laskuvarjonsa?

Kuinka pitkän matkan hyppääjä on edennyt maanpinnan suhteen tässä ajassa?

Kirjataan lähtöarvot

\color{Goldenrod}{y_0}=4 \ 000 \text{ m}, \ \color{CornflowerBlue}{v_{0x}}=400 \text{ km/h}, \
y0=4 000 m, v0x=400 km/h, \color{Goldenrod}{y_0}=4 \ 000 \text{ m}, \ \color{CornflowerBlue}{v_{0x}}=400 \text{ km/h}, \
\color{Goldenrod}{y_1} = 1 \ 500 \text{ m}, \ g=9.81 \text{ m/s}^2
y1=1 500 m, g=9.81 m/s2 \color{Goldenrod}{y_1} = 1 \ 500 \text{ m}, \ g=9.81 \text{ m/s}^2

Piirretään kuva tilanteesta.

Pystysuunnassa hyppääjä on tasaisesti kiihtyvässä liikkeessä.

\color{Goldenrod}{y_1}=\color{Goldenrod}{y_0}-\dfrac{1}{2}gt^2
y1=y0−12gt2\color{Goldenrod}{y_1}=\color{Goldenrod}{y_0}-\dfrac{1}{2}gt^2
||-y_0
∣∣−y0||-y_0
\color{Goldenrod}{y_1}-\color{Goldenrod}{y_0}=-\dfrac{1}{2}gt^2
y1−y0=−12gt2\color{Goldenrod}{y_1}-\color{Goldenrod}{y_0}=-\dfrac{1}{2}gt^2
||\cdot (-2)
∣∣⋅(−2)||\cdot (-2)
\dfrac{-2\color{Goldenrod}{\Delta y}}{g}=t^2
−2Δyg=t2\dfrac{-2\color{Goldenrod}{\Delta y}}{g}=t^2
||\sqrt{}
∣∣||\sqrt{}
t=\pm\sqrt{\dfrac{-2\color{Goldenrod}{\Delta y}}{g}}
t=±−2Δygt=\pm\sqrt{\dfrac{-2\color{Goldenrod}{\Delta y}}{g}}
-2\color{Goldenrod}{\Delta y}=gt^2
−2Δy=gt2-2\color{Goldenrod}{\Delta y}=gt^2
||:g
∣∣:g||:g

1.Vaihe

Sijoitetaan tunnetut arvot ja ratkaistaan aika t.

t=\pm\sqrt{\dfrac{-2\color{Goldenrod}{\Delta y}}{g}}
t=±−2Δygt=\pm\sqrt{\dfrac{-2\color{Goldenrod}{\Delta y}}{g}}
t=\pm\sqrt{\dfrac{-2\cdot \color{Goldenrod}{(-2500 \text{ m})}}{9,81 \text{ m/s}^2}}
t=±−2⋅(−2500 m)9,81 m/s2t=\pm\sqrt{\dfrac{-2\cdot \color{Goldenrod}{(-2500 \text{ m})}}{9,81 \text{ m/s}^2}}
t\approx 22, 6 \text{ s}
t≈22,6 st\approx 22, 6 \text{ s}

2.Vaihe

Maanpinnan suhteen hyppääjän liike on tasaista.  

\color{Goldenrod}{\Delta x} = \color{CornflowerBlue}{v_{0x} }\cdot t
Δx=v0x⋅t\color{Goldenrod}{\Delta x} = \color{CornflowerBlue}{v_{0x} }\cdot t

3.Vaihe

\color{Goldenrod}{\Delta x} = \color{CornflowerBlue}{v_{0x} }\cdot t
Δx=v0x⋅t\color{Goldenrod}{\Delta x} = \color{CornflowerBlue}{v_{0x} }\cdot t
\color{Goldenrod}{\Delta x} = \color{CornflowerBlue}{\dfrac{400}{3,6} \text{ m/s} }\cdot 22,6 \text{ s}
Δx=4003,6 m/s⋅22,6 s\color{Goldenrod}{\Delta x} = \color{CornflowerBlue}{\dfrac{400}{3,6} \text{ m/s} }\cdot 22,6 \text{ s}
\color{Goldenrod}{\Delta x} \approx 2510 \text{ m}
Δx≈2510 m\color{Goldenrod}{\Delta x} \approx 2510 \text{ m}

Vastaus:

Putoaminen kestää noin 23 sekuntia, jonka aikana hyppääjä etenee maanpinnan suhteen 2500 m.

Esimerkki

Kerrostalon katolta heitetään lumipallo vaakasuoraan nopeudella 20 m/s. Lumipallo osuu 1,2 sekunnin päästä 1,5 metrin korkuista lumiukkoa päähän.

Kuinka korkea kerrostalo on?

1.Vaihe

Kirjataan lähtöarvot

\color{CornflowerBlue}{v_{x}}=20 \text{ m/s}, \ t=1,2 \text{ s}
vx=20 m/s, t=1,2 s\color{CornflowerBlue}{v_{x}}=20 \text{ m/s}, \ t=1,2 \text{ s}
\color{Goldenrod}{y_1} = 1,5 \text{ m}, \ g=9.81 \text{ m/s}^2
y1=1,5 m, g=9.81 m/s2 \color{Goldenrod}{y_1} = 1,5 \text{ m}, \ g=9.81 \text{ m/s}^2

Piirretään kuva tilanteesta.

y_0
y0y_0
y_1
y1y_1

Pystysuunnassa lumipallo on tasaisesti kiihtyvässä liikkeessä.

\color{Goldenrod}{y_1}=\color{Goldenrod}{y_0} - \dfrac{1}{2}gt^2
y1=y0−12gt2\color{Goldenrod}{y_1}=\color{Goldenrod}{y_0} - \dfrac{1}{2}gt^2
\color{Goldenrod}{y_1}+\dfrac{1}{2}gt^2=\color{Goldenrod}{y_0}
y1+12gt2=y0\color{Goldenrod}{y_1}+\dfrac{1}{2}gt^2=\color{Goldenrod}{y_0}
||+\frac{1}{2}gt^2
∣∣+12gt2||+\frac{1}{2}gt^2
\color{Goldenrod}{y_0} =\color{Goldenrod}{y_1}+\dfrac{1}{2}gt^2
y0=y1+12gt2\color{Goldenrod}{y_0} =\color{Goldenrod}{y_1}+\dfrac{1}{2}gt^2
y_0
y0y_0
y_1
y1y_1

Sijoitetaan tunnetut lukuarvot.

\color{Goldenrod}{y_0} =\color{Goldenrod}{1,5 \text{ m}}+\dfrac{1}{2} \cdot (9,81 \text{ m/s}^2)\cdot (1,2 \text{ s})^2
y0=1,5 m+12⋅(9,81 m/s2)⋅(1,2 s)2\color{Goldenrod}{y_0} =\color{Goldenrod}{1,5 \text{ m}}+\dfrac{1}{2} \cdot (9,81 \text{ m/s}^2)\cdot (1,2 \text{ s})^2
\color{Goldenrod}{y_1}=\color{Goldenrod}{y_0} - \dfrac{1}{2}gt^2
y1=y0−12gt2\color{Goldenrod}{y_1}=\color{Goldenrod}{y_0} - \dfrac{1}{2}gt^2
\color{Goldenrod}{y_1}+\dfrac{1}{2}gt^2=\color{Goldenrod}{y_0}
y1+12gt2=y0\color{Goldenrod}{y_1}+\dfrac{1}{2}gt^2=\color{Goldenrod}{y_0}
||+\frac{1}{2}gt^2
∣∣+12gt2||+\frac{1}{2}gt^2
\color{Goldenrod}{y_0} =\color{Goldenrod}{y_1}+\dfrac{1}{2}gt^2
y0=y1+12gt2\color{Goldenrod}{y_0} =\color{Goldenrod}{y_1}+\dfrac{1}{2}gt^2
\color{Goldenrod}{y_0} \approx 8,6 \text{ m}
y0≈8,6 m\color{Goldenrod}{y_0} \approx 8,6 \text{ m}

2.Vaihe

Talo on noin 8,6 metriä korkea.

Vastaus:

Tennispallo heitetään 10 metrin korkeudelta vaakasuoraan nopeudella 5,0 m/s. 

Mikä on tennispallon nopeus 1,0 sekunnin kuluttua?

Mikä on tennispallon nopeus 2,0 sekunnin kuluttua?

a)

b)

Esimerkki

Ratkaisu

Kirjataan lähtöarvot

Piirretään kuva tilanteesta.

y_0=10 \text{ m}, \ v_x=5,0 \text{ m/s}, \ g=9,81 \text{ m/s}^2
y0=10 m, vx=5,0 m/s, g=9,81 m/s2y_0=10 \text{ m}, \ v_x=5,0 \text{ m/s}, \ g=9,81 \text{ m/s}^2

Pystysuunnassa pallo on tasaisesti kiihtyvässä liikkeessä.

Vaakasuunnassa pallo on tasaisessa liikkeessä.

1. vaihe

Ratkaistaan pallon lentoaika.

0=y_0-\dfrac{1}{2}gt^2
0=y0−12gt20=y_0-\dfrac{1}{2}gt^2
\dfrac{1}{2}gt^2=y_0
12gt2=y0\dfrac{1}{2}gt^2=y_0
||\cdot 2
∣∣⋅2||\cdot 2
||:g
∣∣:g||:g
gt^2=2y_0
gt2=2y0gt^2=2y_0
t^2=\dfrac{2y_0}{g}
t2=2y0gt^2=\dfrac{2y_0}{g}
||\sqrt{}
∣∣||\sqrt{}
t=\pm \sqrt{\dfrac{2y_0}{g}}
t=±2y0gt=\pm \sqrt{\dfrac{2y_0}{g}}
t= \sqrt{\dfrac{2\cdot 10 \text{ m}}{9,81 \text{ m/s}^2}}
t=2⋅10 m9,81 m/s2t= \sqrt{\dfrac{2\cdot 10 \text{ m}}{9,81 \text{ m/s}^2}}
t \approx 1,43 \text{ s}
t≈1,43 st \approx 1,43 \text{ s}

2. vaihe

Lasketaan hetkellä t = 1,0 s pallon x- ja y-suuntaiset nopeudet.

\color{CornflowerBlue}{v_x}=5,0 \text{ m/s}
vx=5,0 m/s\color{CornflowerBlue}{v_x}=5,0 \text{ m/s}

x-suunnassa liike tasaista.

y-suunnassa liike tasaisesti kiihtyvää.

\color{CornflowerBlue}{v_y}=gt
vy=gt\color{CornflowerBlue}{v_y}=gt
=9,81 \text{ m/s}^2 \cdot 1,0 \text{ s}
=9,81 m/s2⋅1,0 s=9,81 \text{ m/s}^2 \cdot 1,0 \text{ s}
\color{CornflowerBlue}{v_y}=9,81 \text{ m/s}
vy=9,81 m/s\color{CornflowerBlue}{v_y}=9,81 \text{ m/s}
\color{CornflowerBlue}{v_y}
vy\color{CornflowerBlue}{v_y}

3. vaihe

Lasketaan pythagoraan lauseen avulla nopeuden suuruus.

\color{CornflowerBlue}v=\sqrt{\color{CornflowerBlue}{v_x}^2+\color{CornflowerBlue}{v_y}^2}
v=vx2+vy2\color{CornflowerBlue}v=\sqrt{\color{CornflowerBlue}{v_x}^2+\color{CornflowerBlue}{v_y}^2}
\color{CornflowerBlue}v=\sqrt{(\color{CornflowerBlue}{5,0 \text{ m/s}})^2+(\color{CornflowerBlue}{9,81 \text{ m/s}})^2}
v=(5,0 m/s)2+(9,81 m/s)2\color{CornflowerBlue}v=\sqrt{(\color{CornflowerBlue}{5,0 \text{ m/s}})^2+(\color{CornflowerBlue}{9,81 \text{ m/s}})^2}
\color{CornflowerBlue}v \approx 11 \text{ m/s}
v≈11 m/s\color{CornflowerBlue}v \approx 11 \text{ m/s}

Nopeuden suunta saadaan laskettua tangentin avulla.

\tan \color{Salmon} \alpha =\dfrac{\color{CornflowerBlue}{v_y}}{\color{CornflowerBlue}{v_x}}
tanα=vyvx\tan \color{Salmon} \alpha =\dfrac{\color{CornflowerBlue}{v_y}}{\color{CornflowerBlue}{v_x}}
\tan \color{Salmon} \alpha =\dfrac{\color{CornflowerBlue}{9,81 \text{ m/s}}}{\color{CornflowerBlue}{5,0 \text{ m/s}}}
tanα=9,81 m/s5,0 m/s\tan \color{Salmon} \alpha =\dfrac{\color{CornflowerBlue}{9,81 \text{ m/s}}}{\color{CornflowerBlue}{5,0 \text{ m/s}}}
||\tan^{-1}
∣∣tan−1||\tan^{-1}
\color{Salmon}\alpha \approx 63^{\circ}
α≈63∘\color{Salmon}\alpha \approx 63^{\circ}

Vastaus

Hetkellä t = 1,0 s pallon nopeus on 11 m/s ja suunta poikkeaa vaakasuunnasta 63 astetta alaspäin.

Koska pallon lentoaika on noin 1,43 sekuntia, niin pallon nopeus hetkellä t = 2,0 s on 0 m/s.

Koripalloilija heittää koripallon suoraan ylöspäin nopeudella 8,0 m/s. Koripalloilija on 2,0 metriä pitkä. 

Esimerkki

Kuinka korkealla pallo käy?

Millä nopeudella pallo osuu maahan?

Asetetaan potentiaalienergian nollataso maanpinnan tasolle.

Ratkaisu a-kohtaan

Tapa 1

Oletetaan, että koripalloon kohdistuva ilmanvastus on mitätön.

Kirjataan lähtöarvot

v_0=8,0 \text{ m/s}, \ h_0 = 2,0 \text{ m}, g=9,81 \text{ m/s}^2
v0=8,0 m/s, h0=2,0 m,g=9,81 m/s2v_0=8,0 \text{ m/s}, \ h_0 = 2,0 \text{ m}, g=9,81 \text{ m/s}^2

Energian säilymislain nojalla

E_{\text{aluksi}} = E_{\text{lopuksi}}
Ealuksi=ElopuksiE_{\text{aluksi}} = E_{\text{lopuksi}}
h_0+\dfrac{v_0^2}{2g}=h_1
h0+v022g=h1h_0+\dfrac{v_0^2}{2g}=h_1
mgh_0+\dfrac{1}{2}mv_0^2=mgh_1
mgh0+12mv02=mgh1mgh_0+\dfrac{1}{2}mv_0^2=mgh_1
||:mg
∣∣:mg||:mg
h_1 = 2,0 \text{ m} + \dfrac{(8,0 \text{ m/s})^2}{2 \cdot 9,81 \text{ m/s}^2}
h1=2,0 m+(8,0 m/s)22⋅9,81 m/s2h_1 = 2,0 \text{ m} + \dfrac{(8,0 \text{ m/s})^2}{2 \cdot 9,81 \text{ m/s}^2}

Ratkaistaan lakikorkeus

Potentiaali-energia

liike-energia

Potentiaalienergia

aluksi

lopuksi

h_1 \approx 5,3 \text{ m}
h1≈5,3 mh_1 \approx 5,3 \text{ m}

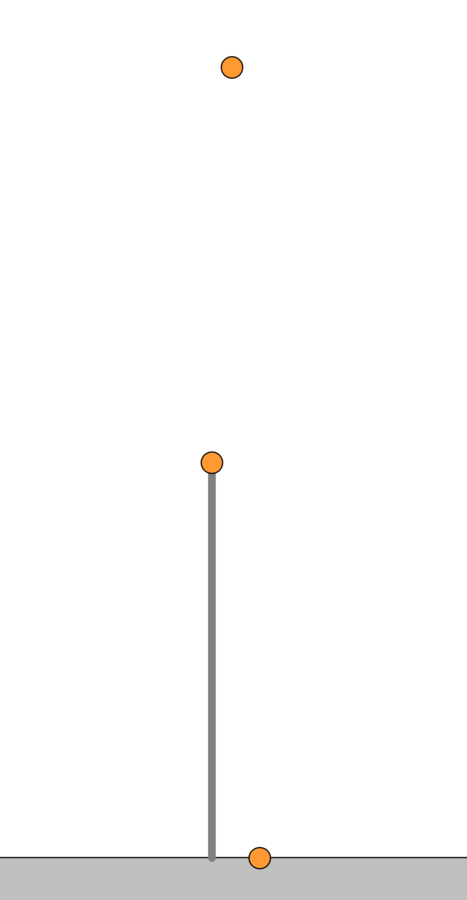
Asetetaan potentiaalienergian nollataso maanpinnan tasolle.

Ratkaisu b-kohtaan

Oletetaan, että koripalloon kohdistuva ilmanvastus on mitätön.

Kirjataan lähtöarvot

v_0=8,0 \text{ m/s}, \ h_0 = 2,0 \text{ m}, g=9,81 \text{ m/s}^2
v0=8,0 m/s, h0=2,0 m,g=9,81 m/s2v_0=8,0 \text{ m/s}, \ h_0 = 2,0 \text{ m}, g=9,81 \text{ m/s}^2

Energian säilymislain nojalla

E_{\text{aluksi}} = E_{\text{lopuksi}}
Ealuksi=ElopuksiE_{\text{aluksi}} = E_{\text{lopuksi}}
2gh_0+v_0^2=v_2^2
2gh0+v02=v222gh_0+v_0^2=v_2^2
mgh_0+\dfrac{1}{2}mv_0^2=\dfrac{1}{2}mv^2_2
mgh0+12mv02=12mv22mgh_0+\dfrac{1}{2}mv_0^2=\dfrac{1}{2}mv^2_2
||:\frac{1}{2}m
∣∣:12m||:\frac{1}{2}m

Ratkaistaan loppunopeus

Potentiaali-energia

liike-energia

liike-energia

aluksi

lopuksi

||\sqrt{}
∣∣||\sqrt{}
v_2=\sqrt{2gh_0+v_0^2}
v2=2gh0+v02v_2=\sqrt{2gh_0+v_0^2}

Energian säilymislain nojalla

E_{\text{aluksi}} = E_{\text{lopuksi}}
Ealuksi=ElopuksiE_{\text{aluksi}} = E_{\text{lopuksi}}
2gh_0+v_0^2=v_2^2
2gh0+v02=v222gh_0+v_0^2=v_2^2
mgh_0+\dfrac{1}{2}mv_0^2=\dfrac{1}{2}mv^2_2
mgh0+12mv02=12mv22mgh_0+\dfrac{1}{2}mv_0^2=\dfrac{1}{2}mv^2_2
||:\frac{1}{2}m
∣∣:12m||:\frac{1}{2}m

Ratkaistaan loppunopeus

Potentiaali-energia

liike-energia

liike-energia

aluksi

lopuksi

||\sqrt{}
∣∣||\sqrt{}
v_2=\sqrt{2gh_0+v_0^2}
v2=2gh0+v02v_2=\sqrt{2gh_0+v_0^2}
v_2=\sqrt{2 \cdot 9,81 \text{ m/s}^2 \cdot 2,0 \text{ m} + (8,0 \text{ m/s})^2}
v2=2⋅9,81 m/s2⋅2,0 m+(8,0 m/s)2v_2=\sqrt{2 \cdot 9,81 \text{ m/s}^2 \cdot 2,0 \text{ m} + (8,0 \text{ m/s})^2}
v_2\approx 10 \text{ m/s}
v2≈10 m/sv_2\approx 10 \text{ m/s}

lakipisteessä koripallo on hetkellisesti levossa, joten

Ratkaisu a-kohtaan

Tapa 2

Ratkaistaan nousuaika

Kirjataan lähtöarvot

v_0=8,0 \text{ m/s}, \ h_0 = 2,0 \text{ m}, g=9,81 \text{ m/s}^2
v0=8,0 m/s, h0=2,0 m,g=9,81 m/s2v_0=8,0 \text{ m/s}, \ h_0 = 2,0 \text{ m}, g=9,81 \text{ m/s}^2
t_1.
t1.t_1.
v_0 - gt_1 = 0.
v0−gt1=0.v_0 - gt_1 = 0.
v_0 = g t_1
v0=gt1v_0 = g t_1
||:g
∣∣:g||:g
t_1 = \dfrac{v_0}{g}
t1=v0gt_1 = \dfrac{v_0}{g}
t_1 = \dfrac{8,0 \text{ m/s}}{9,81 \text{ m/s}^2}
t1=8,0 m/s9,81 m/s2t_1 = \dfrac{8,0 \text{ m/s}}{9,81 \text{ m/s}^2}

Lasketaan lakikorkeus.

h_1=h_0+v_0t_1 - \dfrac{1}{2}gt_1^2
h1=h0+v0t1−12gt12h_1=h_0+v_0t_1 - \dfrac{1}{2}gt_1^2
t_1 \approx 0,816 \text{ s}
t1≈0,816 st_1 \approx 0,816 \text{ s}
h_1=2,0 \text{ m}+8,0 \text{ m/s}\cdot 0,816 \text{ s} - \dfrac{1}{2}\cdot 9,81 \text{ m/s}^2 \cdot (0,816 \text{ s})^2
h1=2,0 m+8,0 m/s⋅0,816 s−12⋅9,81 m/s2⋅(0,816 s)2h_1=2,0 \text{ m}+8,0 \text{ m/s}\cdot 0,816 \text{ s} - \dfrac{1}{2}\cdot 9,81 \text{ m/s}^2 \cdot (0,816 \text{ s})^2
h_1 \approx 5,3 \text{ m}
h1≈5,3 mh_1 \approx 5,3 \text{ m}

Lasketaan aika, joka kuluu että pallo putoaa lakikorkeudelta maanpintaan.

Ratkaisu b-kohtaan

Tapa 2

Kirjataan lähtöarvot

v_0=8,0 \text{ m/s}, \ h_0 = 2,0 \text{ m}, g=9,81 \text{ m/s}^2
v0=8,0 m/s, h0=2,0 m,g=9,81 m/s2v_0=8,0 \text{ m/s}, \ h_0 = 2,0 \text{ m}, g=9,81 \text{ m/s}^2
h_1 - \dfrac{1}{2}gt^2=0
h1−12gt2=0h_1 - \dfrac{1}{2}gt^2=0
h_1 = \dfrac{1}{2}gt^2
h1=12gt2h_1 = \dfrac{1}{2}gt^2
t^2=\dfrac{2h_1}{g}
t2=2h1gt^2=\dfrac{2h_1}{g}
||:\dfrac{1}{2}g
∣∣:12g||:\dfrac{1}{2}g
||\sqrt{}
∣∣||\sqrt{}
t=\sqrt{\dfrac{2h_1}{g}}
t=2h1gt=\sqrt{\dfrac{2h_1}{g}}
t=\sqrt{\dfrac{2 \cdot 5,26 \text{ m}}{9,81 \text{ m/s}^2}}
t=2⋅5,26 m9,81 m/s2t=\sqrt{\dfrac{2 \cdot 5,26 \text{ m}}{9,81 \text{ m/s}^2}}
t \approx 1,04 \text{ s}
t≈1,04 st \approx 1,04 \text{ s}
v_2 = g t
v2=gtv_2 = g t
v_2 = 9,81 \text{ m/s}^2 \cdot 1,04 \text{ s}
v2=9,81 m/s2⋅1,04 sv_2 = 9,81 \text{ m/s}^2 \cdot 1,04 \text{ s}
v_2 \approx 10 \text{ m/s}
v2≈10 m/sv_2 \approx 10 \text{ m/s}

Lasketaan loppunopeus

Mitä ihmettä?

Tikalla tähdätään maalitauluun. Kun tikka ammutaan kohti maalitaulua, niin maalitaulu putoaa. Miksi tikka osuu maalitauluun?

Vaakasuora heittoliike

Vino heittoliike