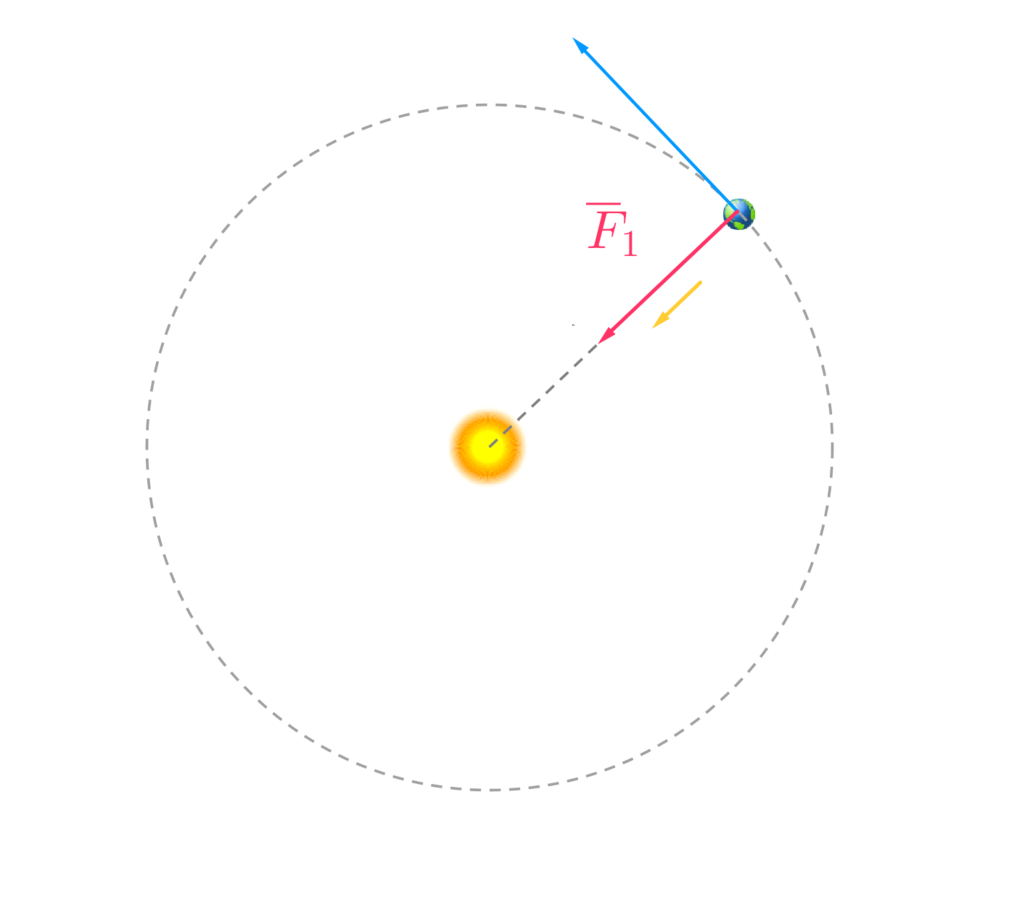
Esimerkki

Määritä Auringon massa käyttäen hyväksesi seuraavia oletuksia ja tietoja:

Maa kiertää Aurinkoa ympyrärataa

Maan ja Auringon välinen keskietäisyys on

1,4960 \cdot 10^8 \text{ km}

1,4960 \cdot 10^8 \text{ km}

Maan kiertoaika Auringon ympäri 365,25 d

Ratkaisu

Kirjataan lähtöarvot

r=1,4960\cdot10^8 \text{ km} = 1,4960 \cdot 10^{11} \text{ m}

r = 1, 4960 \cdot 1 0 ​ 8 ​ ​ k m = 1, 4960 \cdot 1 0 ​ 11 ​ ​ m

T=365,25 \text{ d}

T = 365, 25 d

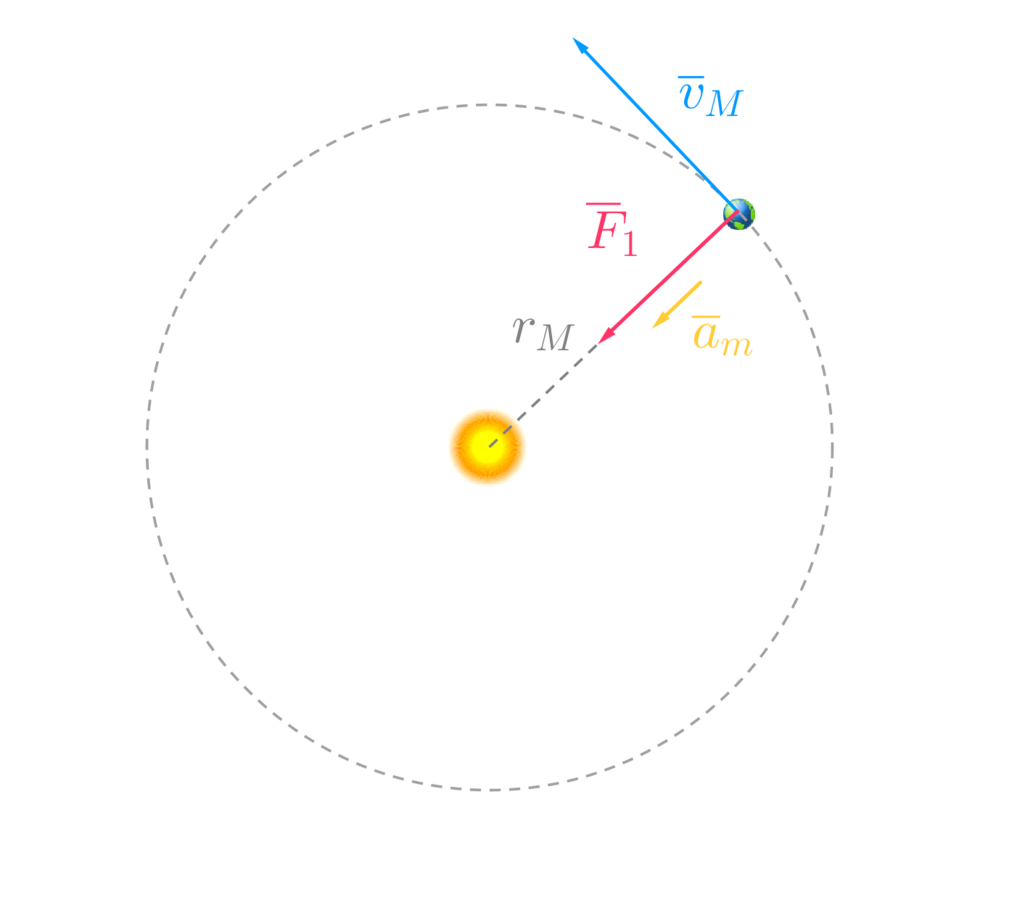
Oletetaan, että Maapallo kiertää ympyrärataa tasaisesti.

\text{NII} \ \sum \overline{F}=m\overline{a}

N I I \sum ​ F ​ ​ ​ = m ​ a ​ ​ ​

\color{Salmon}{F_1}=m\color{Goldenrod}{a_n}

F ​ 1 ​ ​ = m a ​ n ​ ​

a_n=\frac{v_m^2}{r}

a ​ n ​ ​ = \frac{​ v ​ m ​ 2 ​ ​ ​ ​}{​ r ​}

F_1=\gamma \frac{Mm}{r^2}

F ​ 1 ​ ​ = γ \frac{​ M m ​ ​}{​ r ​ 2 ​ ​ ​}

\gamma \dfrac{Mm}{r^2}=m\dfrac{\color{CornflowerBlue}{v}^2}{r}

γ \frac{​ M m ​ ​}{​ r ​ 2 ​ ​ ​} = m \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

: m

\gamma \dfrac{M}{r^2}=\dfrac{\color{CornflowerBlue}{v}^2}{r}

γ \frac{​ M ​ ​}{​ r ​ 2 ​ ​ ​} = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

M

m

\overline{v}

​ v ​ ​ ​

\overline{a}_n

​ a ​ ​ ​ ​ n ​ ​

M=\dfrac{r\color{CornflowerBlue}{v}^2}{\gamma}

M = \frac{​ r v ​ 2 ​ ​ ​ ​}{​ γ ​}

\cdot r^2

\cdot r ​ 2 ​ ​

\gamma \dfrac{M}{r^2}=\dfrac{\color{CornflowerBlue}{v}^2}{r}

γ \frac{​ M ​ ​}{​ r ​ 2 ​ ​ ​} = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\gamma M=r\color{CornflowerBlue}{v}^2

γ M = r v ​ 2 ​ ​

: \gamma

: γ

Toisaalta ratanopeus saadaan kirjoitettua muotoon

\color{CornflowerBlue}v=\dfrac{2 \pi r}{T}

v = \frac{​ 2 π r ​ ​}{​ T ​}

M

m

\overline{v}

​ v ​ ​ ​

\overline{a}_n

​ a ​ ​ ​ ​ n ​ ​

M=\dfrac{r\color{CornflowerBlue}{v}^2}{\gamma}

M = \frac{​ r v ​ 2 ​ ​ ​ ​}{​ γ ​}

v=\dfrac{2 \pi r}{T}

v = \frac{​ 2 π r ​ ​}{​ T ​}

M

m

\overline{v}

​ v ​ ​ ​

\overline{a}_n

​ a ​ ​ ​ ​ n ​ ​

M=\dfrac{r\cdot \Big( \frac{2 \pi r}{T}\Big)^2}{\gamma}

M = \frac{​ r \cdot ( \frac{​ 2 π r ​ ​}{​ T ​} ) ​ 2 ​ ​ ​ ​}{​ γ ​}

M=\dfrac{4 \pi^2 r^3}{\gamma T}

M = \frac{​ 4 π ​ 2 ​ ​ r ​ 3 ​ ​ ​ ​}{​ γ T ​}

Sijoitetaan lukuarvot

M=\dfrac{4 \pi^2 \cdot \Big( 1,4960 \cdot 10^{11} \text{ m}\Big)^3}{6,67384 \cdot 10^{-11} \frac{\text{ Nm}^2}{\text{ kg}^2} \cdot (365,25 \cdot 24 \cdot 60 \cdot 60 \text{ s})^2}

M = \frac{​ 4 π ​ 2 ​ ​ \cdot ( 1 , 4 9 6 0 \cdot 1 0 ​ 1 1 ​ ​ m ) ​ 3 ​ ​ ​ ​}{​ 6 , 6 7 3 8 4 \cdot 1 0 ​ - 1 1 ​ ​ \frac{​ N m ​ 2 ​ ​ ​ ​}{​ k g ​ 2 ​ ​ ​} \cdot ( 3 6 5 , 2 5 \cdot 2 4 \cdot 6 0 \cdot 6 0 s ) ​ 2 ​ ​ ​}

M

m

\overline{v}

​ v ​ ​ ​

\overline{a}_n

​ a ​ ​ ​ ​ n ​ ​

M=\dfrac{4 \pi^2 \cdot \Big( 1,4960 \cdot 10^{11} \text{ m}\Big)^3}{6,67384 \cdot 10^{-11} \frac{\text{ Nm}^2}{\text{ kg}^2} \cdot (365,25 \cdot 24 \cdot 60 \cdot 60 \text{ s})^2}

M = \frac{​ 4 π ​ 2 ​ ​ \cdot ( 1 , 4 9 6 0 \cdot 1 0 ​ 1 1 ​ ​ m ) ​ 3 ​ ​ ​ ​}{​ 6 , 6 7 3 8 4 \cdot 1 0 ​ - 1 1 ​ ​ \frac{​ N m ​ 2 ​ ​ ​ ​}{​ k g ​ 2 ​ ​ ​} \cdot ( 3 6 5 , 2 5 \cdot 2 4 \cdot 6 0 \cdot 6 0 s ) ​ 2 ​ ​ ​}

M \approx 1,9887\cdot 10^{30} \text{ kg}

M \approx 1, 9887 \cdot 1 0 ​ 30 ​ ​ k g

Fysiikan ylioppilaskoe S2006

Ratkaisu

Kirjataan lähtöarvot

r_M=21 \ 000 R ,

r ​ M ​ ​ = 21000 R,

r_K = 60 R ,

r ​ K ​ ​ = 60 R,

T_K = 27,3 \text{ d}

T ​ K ​ ​ = 27, 3 d

T_M = 365 \text{ d}

T ​ M ​ ​ = 365 d

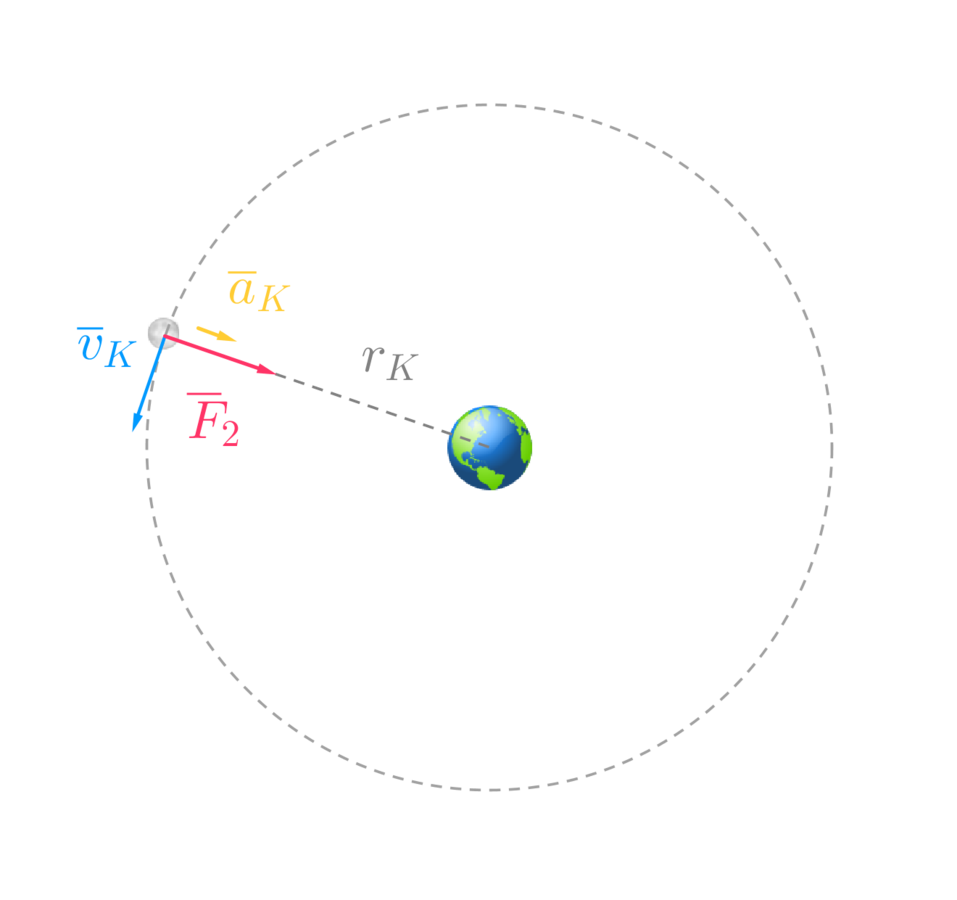
Oletetaan, että Kuu ja Maapallo ovat tasaisessa ympyräliikkeessä.

Newtonin 2. lain mukaan

\sum \overline{F}=m_1\overline{a}

\sum ​ F ​ ​ ​ = m ​ 1 ​ ​ ​ a ​ ​ ​

Newtonin gravitaatiolain nojalla saadaan

\gamma \dfrac{m_1m_2}{r^2}=m_1\dfrac{v^2}{r}

γ \frac{​ m ​ 1 ​ ​ m ​ 2 ​ ​ ​ ​}{​ r ​ 2 ​ ​ ​} = m ​ 1 ​ ​ \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\gamma \dfrac{m_2}{r^2}=\dfrac{v^2}{r}

γ \frac{​ m ​ 2 ​ ​ ​ ​}{​ r ​ 2 ​ ​ ​} = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\gamma \dfrac{m_2}{r}=v^2

γ \frac{​ m ​ 2 ​ ​ ​ ​}{​ r ​} = v ​ 2 ​ ​

F=m_1a

F = m ​ 1 ​ ​ a

:m_1

: m ​ 1 ​ ​

a=\frac{v^2}{r}

a = \frac{​ v ​ 2 ​ ​ ​ ​}{​ r ​}

\cdot r

\cdot r

Kappaleet kiertävät ympyrärataa, joten toisaalta ratanopeus saadaan kirjoitettua muotoon

v=\dfrac{2 \pi r}{T}

v = \frac{​ 2 π r ​ ​}{​ T ​}

\gamma \dfrac{m_2}{r}=v^2

γ \frac{​ m ​ 2 ​ ​ ​ ​}{​ r ​} = v ​ 2 ​ ​

\gamma \dfrac{m_2}{r}=\dfrac{4 \pi^2 r^2}{T^2}

γ \frac{​ m ​ 2 ​ ​ ​ ​}{​ r ​} = \frac{​ 4 π ​ 2 ​ ​ r ​ 2 ​ ​ ​ ​}{​ T ​ 2 ​ ​ ​}

\cdot \dfrac{r}{\gamma}

\cdot \frac{​ r ​ ​}{​ γ ​}

m_2=\dfrac{4 \pi^2 r^3}{\gamma T^2}

m ​ 2 ​ ​ = \frac{​ 4 π ​ 2 ​ ​ r ​ 3 ​ ​ ​ ​}{​ γ T ​ 2 ​ ​ ​}

Kappale, jota kierretään

Nyt saadaan kirjoitettua Auringon ja Maapallon massoille lausekkeet

m_A=\dfrac{4 \pi^2 r_M^3}{\gamma T_M^2}

m ​ A ​ ​ = \frac{​ 4 π ​ 2 ​ ​ r ​ M ​ 3 ​ ​ ​ ​}{​ γ T ​ M ​ 2 ​ ​ ​}

m_M=\dfrac{4 \pi^2 r_K^3}{\gamma T_K^2}

m ​ M ​ ​ = \frac{​ 4 π ​ 2 ​ ​ r ​ K ​ 3 ​ ​ ​ ​}{​ γ T ​ K ​ 2 ​ ​ ​}

Lasketaan Auringon ja Maapallon massojen suhde.

\dfrac{m_A}{m_M}=\dfrac{4 \pi^2 r_M^3}{\gamma T_M^2} : \dfrac{4 \pi^2 r_K^3}{\gamma T_K^2}

\frac{​ m ​ A ​ ​ ​ ​}{​ m ​ M ​ ​ ​} = \frac{​ 4 π ​ 2 ​ ​ r ​ M ​ 3 ​ ​ ​ ​}{​ γ T ​ M ​ 2 ​ ​ ​} : \frac{​ 4 π ​ 2 ​ ​ r ​ K ​ 3 ​ ​ ​ ​}{​ γ T ​ K ​ 2 ​ ​ ​}

\dfrac{m_A}{m_M}=\dfrac{4 \pi^2 r_M^3}{\gamma T_M^2} \cdot \dfrac{\gamma T_K^2}{4 \pi^2 r_K^3}

\frac{​ m ​ A ​ ​ ​ ​}{​ m ​ M ​ ​ ​} = \frac{​ 4 π ​ 2 ​ ​ r ​ M ​ 3 ​ ​ ​ ​}{​ γ T ​ M ​ 2 ​ ​ ​} \cdot \frac{​ γ T ​ K ​ 2 ​ ​ ​ ​}{​ 4 π ​ 2 ​ ​ r ​ K ​ 3 ​ ​ ​}

\dfrac{m_A}{m_M}=\dfrac{ T_K^2 r_M^3 }{ T_M^2 r_K^3}

\frac{​ m ​ A ​ ​ ​ ​}{​ m ​ M ​ ​ ​} = \frac{​ T ​ K ​ 2 ​ ​ r ​ M ​ 3 ​ ​ ​ ​}{​ T ​ M ​ 2 ​ ​ r ​ K ​ 3 ​ ​ ​}

\dfrac{m_A}{m_M}=\dfrac{ (27,3 \text{ d})^2 \cdot (21 \ 000R)^3 }{(365 \text{ d})^2 \cdot (60 R)^3}

\frac{​ m ​ A ​ ​ ​ ​}{​ m ​ M ​ ​ ​} = \frac{​ ( 2 7 , 3 d ) ​ 2 ​ ​ \cdot ( 2 1 0 0 0 R ) ​ 3 ​ ​ ​ ​}{​ ( 3 6 5 d ) ​ 2 ​ ​ \cdot ( 6 0 R ) ​ 3 ​ ​ ​}

Sijoitetaan lukuarvot

\approx 240 \ 000

\approx 240000

Vastaus

Auringon massa on noin 240 000 -kertainen Maan massaan verrattuna.