MAA12: Algoritmit matematiikassa
Numeeriset menetelmät
Esimerkki 1
Määritä funktion nollakohta kahden desimaalin tarkkuudella liikuttamalla oheisen sovelman pisteitä .
Numeeriset menetelmät
- Mikäli funktion nollakohtaa tai yhtälön ratkaisua ei pystytä selvittämään tarkasti – tai jos tarkkaa arvoa ei tarvita – sitä voidaan etsiä jollakin numeerisella menetelmällä.
- Numeerisia menetelmiä on useita.
Haarukointi
- Menetelmää, jossa jatkuvan funktion nollakohta eristetään yhä pienemmälle välille hyödyntämällä funktion arvoja ja Bolzanon lausetta, kutsutaan haarukoinniksi.
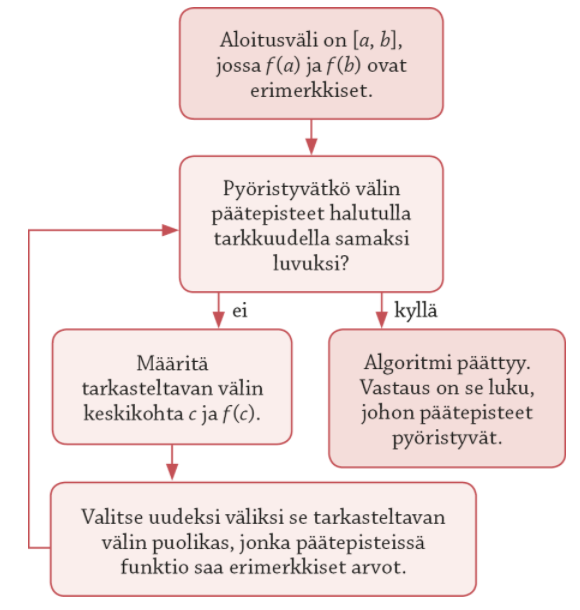
- Yksinkertaisin haarukointialgoritmi on puolitusmenetelmä, jossa väli aina puolitetaan ja uudeksi tarkasteluväliksi valitaan se puolikkaista, jolla funktion merkki vaihtuu. Ensimmäinen tarkasteluväli valitaan esimerkiksi kuvan avulla.
Bolzanon lause
Jos funktio f(x) on jatkuva suljetulla välillä [a, b] ja sen arvot päätepisteissä ovat erimerkkiset (f(a)f(b)<0), on sillä avoimella välillä ]a, b[ nollakohta f(c)=0.
Esimerkki 2
Määritä puolitusmenetelmällä funktion f nollakohta kahden desimaalin tarkkuudella, kun tiedetään, että nollakohta on välillä ]-2, -1[.
Ratkaisu:
Koska funktio f on suljetulla välillä [-2, -1] jatkuva ja sen arvot ovat välin päätepisteissä erimerkkiset, on sillä Bolzanon lauseen nojalla nollakohta välillä ]-2, -1[.
Bolzanon lause
Jos funktio f(x) on jatkuva suljetulla välillä [a, b] ja sen arvot päätepisteissä ovat erimerkkiset (f(a)f(b)<0), on sillä avoimella välillä ]a, b[ nollakohta f(c)=0.
Yritetään siis supistaa väli ]a, b[ mahdollisimman pieneksi niin, että f(a)f(b)<0, jolloin väliltä löytyy arvo c, jolla f(c)=0.
Puolitusmenetelmä taulukkolaskentaohjelmalla
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | a | c=(a+b)/2 | b | f(a) | f(c) | f(a)f(c) |
| 2 | (A2+C2)/2 | D2*E2 | ||||
| 3 | Jos(F2<0,A2,B2) | Jos(F2<0,B2,C2) |
- Muistutuksena, mitä kirjoitetaan taulukkolaskentaohjelmaan
- Rivillä 1 otsikoita
Puolitusmenetelmän algoritmi
Newtonin menetelmä
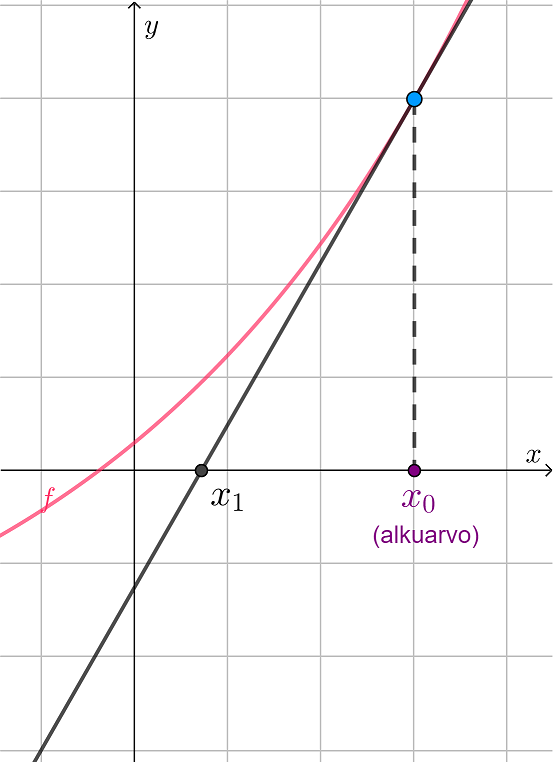
Nollakohdan määrittäminen tangentin avulla
- Funktion f kuvaajalle piirrettyjen tangenttien leikkauskohdat x-akselin kanssa lähestyvät funktion f nollakohtaa, kun uusi tangentti piirretään aina edellisen tangentin ja x-akselin leikkauskohtaan
- Tangentti approksimoi funktion kuvaajaa ja tangenttisuoran nollakohta funktion nollakohtaa. Toistamalla algoritmia arvio yleensä paranee.
Tangentin yhtälö
Newtonin menetelmän rekursiokaava
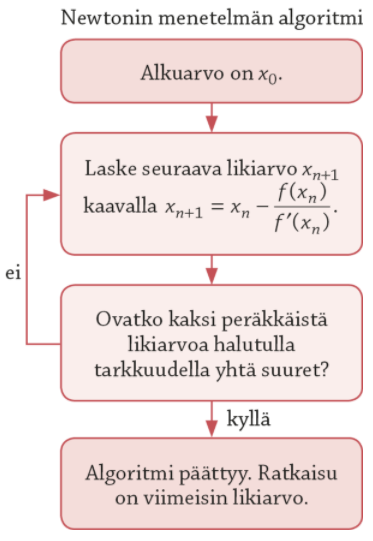
Oletetaan, että funktio f on derivoituva.
Funktion f nollakohdan ensimmäinen likiarvo eli alkuarvo on x0.
Seuraavat likiarvot lasketaan kaavalla
Newtonin menetelmän algoritmi
Esimerkki 1
Newtonin menetelmä taulukkolaskentaohjelmalla
Määritä funktion f nollakohta Newtonin menetelmällä. Käytä alkuarvona x0 = 1.
| A | B | |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 1 | =B1-((e^((B1+1)/2)-1.5)/(1/2*e^((B1+1)/2))) |
| 3 | 2 | |
| 4 | 3 |
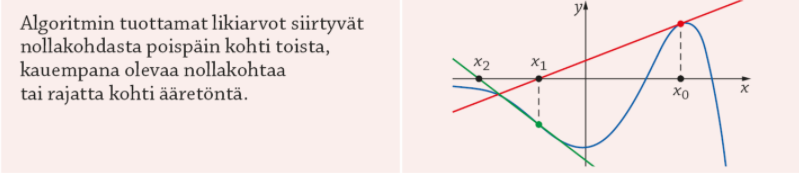
Tilanteita, joissa Newtonin menetelmä ei toimi


Kiintopistemenetelmä
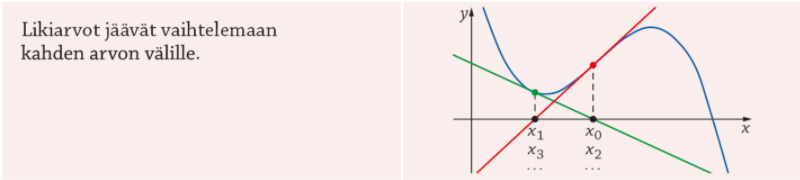
- Yhtälön 𝑥 = 𝑔(𝑥) ratkaisua 𝑥 = 𝑎 kutsutaan funktion 𝑔 kiintopisteeksi.
- Geometrisesti kiintopisteen voi määrittää käyrän 𝑦 = 𝑔(𝑥) ja suoran 𝑦 = 𝑥 leikkauspisteen 𝑥 −koordinaatista.
- Kiintopistemenetelmä on algoritmi, jota voidaan käyttää ainakin joissakin tapauksissa yhtälön numeeriseen ratkaisemiseen:
- Muokkaa ratkaistava yhtälö muotoon 𝑥 = 𝑔(𝑥)
- Valitaan jokin alkuarvo (likiarvo) 𝑥0
- Lasketaan ratkaisun likiarvoja rekursiivisesti kaavalla
- Jatketaan, kunnes haluttu tarkkuus on saavutettu (eli peräkkäiset likiarvot kyseisellä tarkkuudella samat)
- Ratkaistava yhtälö voidaan yleensä muokata usealla tavalla muotoon 𝑥 = 𝑔(𝑥)
- Kiintopistemenetelmän toimivuus riippuu alkuarvon 𝑥0 valinnan lisäksi funktion 𝑔 valinnasta
Esimerkki
Funktion f toinen nollakohta on positiivinen. Määritä tämä nollakohta kiintopistemenetelmällä viiden desimaalin tarkkuudella.
Muokataan funktion lauseke muotoon
ei toimi (voidaan kokeilla kyllä sitäkin)
- Halutaan ratkaista positiivinen nollakohta, joten tarkastellaan funktiota
- Piirretään GeoGebraan funktion g(x) kuvaaja.
- Avataan Taulukkolaskenta-näkymä.
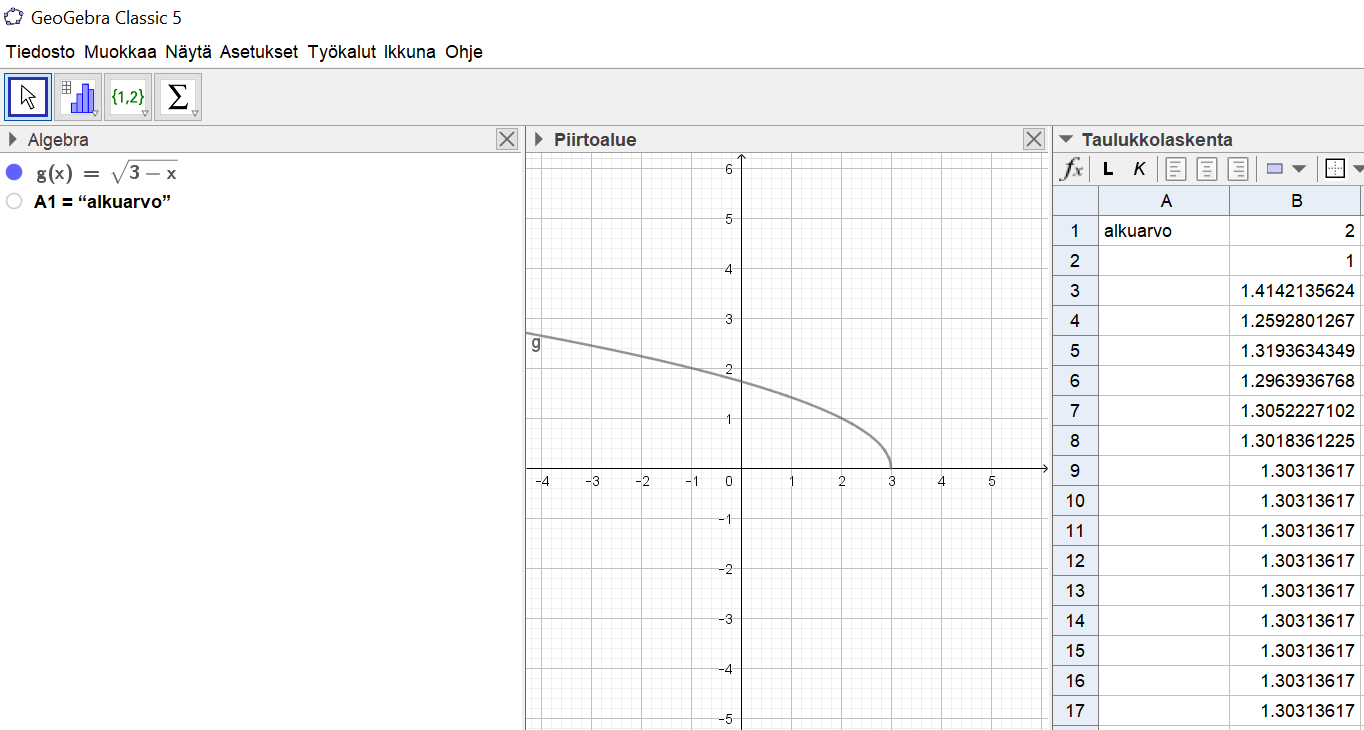
- Valitaan alkuarvoksi esim. x=2. Kirjoitetaan taulukkolaskentaohjelman soluun B1 2.
- Kirjoitetaan soluun B2 g(B1) ja kopioidaan solua. Jatketaan kopiointia, kunnes arvo pysyy halutulla tarkkuudella samana.