Radiaanit

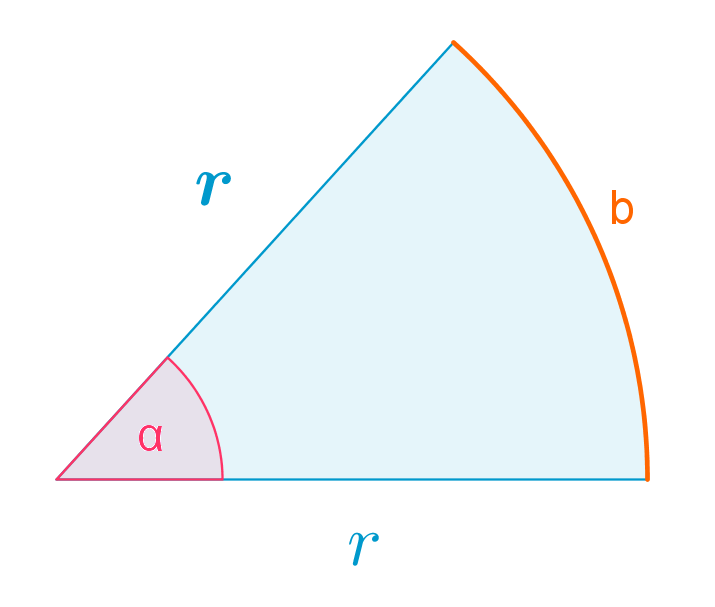
\color{Salmon}\alpha=\dfrac{\color{Orange}b}{\color{CornflowerBlue}r}
α=rb
Kulma radiaaneina määritellään ympyräkaaren pituuden ja ympyrän säteen suhteena
360^{\circ}=2\pi \text{ rad}
360∘=2π rad
180^{\circ}=\pi \text{ rad}
180∘=π rad
Kulma radiaaneina
Esimerkki
Määritä radiaaneina
90^{\circ}, \ 45^{\circ} \text{ ja } 330 ^{\circ}
90∘, 45∘ ja 330∘
180^{\circ} = \pi \ \text{rad}
180∘=π rad
90^{\circ} =\dfrac{ \pi}{2} \ \text{rad}
90∘=2π rad
45^{\circ} =\dfrac{ \pi}{4} \ \text{rad}
45∘=4π rad
180^{\circ} = \pi \text{ rad}
180∘=π rad
1^{\circ}= \dfrac{\pi}{180} \text{ rad}
1∘=180π rad
330^{\circ}=330 \cdot \dfrac{\pi}{180} \text{ rad}
330∘=330⋅180π rad
330^{\circ}=\dfrac{11\pi}{6} \text{ rad}
330∘=611π rad
\qquad ||:2
∣∣:2
\qquad ||:2
∣∣:2
\qquad ||:180
∣∣:180
\qquad ||\cdot 330
∣∣⋅330
Esimerkki
Määritä asteina 3 ja 0,5
\pi \ \text{rad}=180^{\circ}
π rad=180∘
1 \text{ rad}= \ \dfrac{180}{\pi}^{\circ}
1 rad= π180∘
\qquad ||:\pi
∣∣:π
\qquad ||\cdot 3
∣∣⋅3
3 \text{ rad}=\ \dfrac{540}{\pi}^{\circ}
3 rad= π540∘
1 \text{ rad}=\ \dfrac{180}{\pi}^{\circ}
1 rad= π180∘
\qquad ||:2
∣∣:2
0,5 \text{ rad}= \ \dfrac{90}{\pi}^{\circ}
0,5 rad= π90∘
3 \text{ rad}\approx 171,9^{\circ}
3 rad≈171,9∘
0,5 \text{ rad} \approx 28,6^{\circ}
0,5 rad≈28,6∘
Yksikköympyrä
Trigonometriset funktiot voidaan määritellä yleisemmin yksikköympyrän avulla.
Huomataan, että yksikköympyrän kehäpisteen koodinaatit voidaan ilmaista sinin ja kosinin avulla.
P(\cos \alpha, \sin \alpha)
P(cosα,sinα)
P(x, \ y)
P(x, y)
=
Esimerkki
Määritä yksikköympyrän avulla
\sin 30^{\circ}, \ \cos 60^{\circ}
sin30∘, cos60∘
\text{ ja } \sin 135^{\circ}
ja sin135∘
Ratkaisu
\sin 30^{\circ}\approx 0,5
sin30∘≈0,5
\cos 60^{\circ}\approx 0,5
cos60∘≈0,5
\sin 135^{\circ}\approx 0,71
sin135∘≈0,71
Sinin symmetria
Kosinin parillisuus
Kosinin parillisuus
Sinin symmetria
\sin \alpha = \sin(180^{\circ}-\alpha)
sinα=sin(180∘−α)
\cos \alpha=\cos (-\alpha)
cosα=cos(−α)
Jaksollisuus
\sin \alpha = \sin (\alpha + n \cdot 360^{\circ}), \ n=0, \pm 1, \pm 2 \ldots
sinα=sin(α+n⋅360∘), n=0,±1,±2…
\cos \alpha = \cos (\alpha + n \cdot 360^{\circ}), \ n=0, \pm 1, \pm 2 \ldots
cosα=cos(α+n⋅360∘), n=0,±1,±2…
Sini- ja kosinifunktion kuvaajat
Tangenttifunktio
\sin \alpha = y
sinα=y
\cos \alpha = x
cosα=x
\tan \alpha=\dfrac{y}{x}
tanα=xy
\tan \alpha=\dfrac{\sin \alpha}{\cos \alpha}
tanα=cosαsinα
Esimerkki
Määritä yksikköympyrän avulla
\text{a) } \sin (-130^{\circ}), \ \text{b) } \cos \dfrac{3 \pi}{2},
a) sin(−130∘), b) cos23π,
\sin (-130^{\circ}) \approx -0,8
sin(−130∘)≈−0,8
\pi \text{ rad} = 180^{\circ}
π rad=180∘
\dfrac{3\pi }{2} \text{ rad}= 270^{\circ}
23π rad=270∘
\cos 270^{\circ}\approx 0
cos270∘≈0
a-kohta
b-kohta
\pi \text{ rad} = 180^{\circ}
π rad=180∘
\tan 30^{\circ}=\dfrac{\sin 30^{\circ}}{\cos 30^{\circ}}
tan30∘=cos30∘sin30∘
\dfrac{\pi}{6} \text{ rad} = 30^{\circ}
6π rad=30∘
\tan \dfrac{\pi}{6}
tan6π
Esimerkki
Määritä yksikköympyrän avulla
Ratkaisu
\cos 30^{\circ}=0,87
cos30∘=0,87
\sin 30^{\circ}=0,50
sin30∘=0,50
\tan 30^{\circ}=\dfrac{0,50}{0,87}
tan30∘=0,870,50
\tan 30^{\circ} \approx 0,57
tan30∘≈0,57
Esimerkki
Millaisia arvoja lausekkeet voivat saada?
\text{a) }1+\sin x
a) 1+sinx
\text{b) }-1+2\cos x
b) −1+2cosx
Ratkaisu
\text{a) }
a)
0\leq1+\sin x\leq 2
0≤1+sinx≤2
-1 \leq \sin x \leq 1
−1≤sinx≤1
, joten
\text{b) }
b)
-1 \leq \cos x \leq 1
−1≤cosx≤1
-2 \leq 2\cos x \leq 2
−2≤2cosx≤2
, joten
-3 \leq -1+2\cos x \leq 1
−3≤−1+2cosx≤1
. Nyt