Sistemas Inteligentes
Unidad 2: Lógica Difusa Tipo – I
Ing. Oscar Alonso Rosete Beas
Semana 18 Marzo Rev:1 ciclo 2021-1
oscarrosete.com
oscarrosete.com

Agenda
2.1. Introducción a la Lógica Difusa
2.2. Conjuntos difusos y funciones de membresía
2.3. Operaciones sobre conjuntos difusos
2.4. Inferencia usando Lógica Difusa
2.5. Diseño de clasificadores difusos
Unidad 2: Lógica Difusa Tipo – I
oscarrosete.com
Unidad 2
oscarrosete.com

oscarrosete.com

oscarrosete.com
Agenda
2.1. Introducción a la Lógica Difusa
2.2. Conjuntos difusos y funciones de membresía
2.3. Operaciones sobre conjuntos difusos
2.4. Inferencia usando Lógica Difusa
2.5. Diseño de clasificadores difusos
Unidad 2: Lógica Difusa Tipo – I
oscarrosete.com

oscarrosete.com
Lógica difusa vs lógica clásica
También llamada lógica clásica o booleana, esta fundamentada en la lógica aristotélica.
Solamente existen dos posibles valores de veracidad, donde la verdad (T) y la falsedad (F) pueden ser cualquier número en [0,1] tal que T+F=1.
Lógica aristotélica
Neutrosophic computing and machine learning

oscarrosete.com

oscarrosete.com
Lógica difusa vs lógica clásica
Gama de posibilidades de veracidad
No solo 2 posibles estados, permite valores intermedios para poder definir evaluaciones convencionales, valores entre 0 y 1.
¿Qué propone la lógica difusa?

oscarrosete.com

oscarrosete.com
Lógica difusa vs lógica clásica
Ejemplo
¿Qué tan mojada está la ropa?


oscarrosete.com

oscarrosete.com
Utilidad
El uso de técnicas de lógica difusa en control automático trata de imitar o emular el comportamiento consciente de un operador humano en el gobierno de procesos, sistemas o plantas alineales reales, los que difícilmente pueden ser modelados por los métodos fisicomatemáticos usuales.
Trasladar experiencia humana a computadora

oscarrosete.com

oscarrosete.com
Utilidad
Método básico: Traducir la experiencia o forma de trabajo de la persona experta en manipulación o control de una maquinaria en reglas lingüísticas que las comprenda una computadora.
Potencial propósito: Diseñar un controlador difuso que complemente o sustituya la operación manual.
Trasladar experiencia humana a computadora

oscarrosete.com

oscarrosete.com
Utilidad
La información que proviene de nuestro entorno que obtenemos a través de sentidos, aparatos de medición, etc tiene errores y la manera clásica de procesar la información para obtener conclusiones es utilizando teoría de probabilidad y estadística.
Otra alternativa es utilizar un razonamiento aproximado de la lógica difusa.
Procesar información con incertidumbre:

oscarrosete.com

oscarrosete.com
Control difuso
¿En qué difiere el control difuso al control convencional?
El enfoque tradicional desarrollado estuvo basado en problemas muy bien definidos con modelos precisos pero carecen de autonomía y la habilidad de la toma de decisiones.
La problemática es utilizarlos en entornos inciertos.
Intelligent Systems: Modeling, Optimization, and Control
By Yung C. Shin, Chengying Xu
oscarrosete.com

oscarrosete.com
No necesitamos modelo matemático, no se requiere identificar el sistema , lo cual lo hace más eficiente en términos del tiempo.
No necesitamos linealizarlo.
Facilita el diseño del controlador.
Desventajas:
Necesitamos conocer las reglas lingüísticas de control de un experto, en el control de cierta maquinaria o cierto sistema y traducir a reglas si y entonces de control
Ventajas
Control difuso
oscarrosete.com

oscarrosete.com
Cuando no conoces el modelo, tenemos 2 alternativas:
Control pid (una entrada y una salida)
Control difuso (multiples entradas y salidas)

Control difuso
¿En qué difiere el control difuso al control convencional?
oscarrosete.com

oscarrosete.com
Control difuso
Potenciales aplicaciones
oscarrosete.com

oscarrosete.com
Cambio fundamental de permitir que las afirmaciones tomen una gama de valores de veracidad entre 0 y 1
¿Qué puede cambiar en las matemáticas?
¿Qué implica el cambio de conjuntos clásicos a conjuntos difusos?
Las aplicaciones todavía se encuentran en investigación.
Fundamentos del control difuso

oscarrosete.com

oscarrosete.com
Nuestro enfoque será en la aplicación de lógica difusa para entender la teoría detrás de los controladores difusos (Mamdani, tsukamoto, Sugeno)
Las aplicaciones todavía se encuentran en investigación.
Fundamentos del control difuso

oscarrosete.com
oscarrosete.com
- Control de dosificación en las plantas de tratamiento de aguas residuales.
- Control de robots en inspección de túneles
- Posicionamiento en prensas
- Control de temperatura en máquinas de moldeo de plástico
- Climatización y automatización de edificios.
Aplicaciones específicas adicionales

oscarrosete.com

oscarrosete.com
Agenda
2.1. Introducción a la Lógica Difusa
2.2. Conjuntos difusos y funciones de membresía
2.3. Operaciones sobre conjuntos difusos
2.4. Inferencia usando Lógica Difusa
2.5. Diseño de clasificadores difusos
Unidad 2: Lógica Difusa Tipo – I
oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Un conjunto es un grupo de elementos u objetos especificados de tal forma que se pueda afirmar con certeza que un objeto dado pertenece o no al conjunto. En general, para denotar a los conjuntos se usan las letras mayúsculas, y letras minúsculas para sus elementos.
Conjuntos
oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Para los conjuntos y sus elementos se utilizan símbolos de pertenencia e igualdad.
Conjuntos

oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Ejemplo


oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Conjuntos clásicos (certeros)
Potencial criterio para diferenciar altos de bajos, quizás altura promedio.
Todos los que estén abajo del promedio serán clasificados como bajos.
Clasifique a las personas de acuerdo con su estatura en dos conjuntos


oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Conjuntos difusos
Todas las personas pertenecen en cierta medida a ambos conjuntos.
Por ejemplo la persona mas alta del grupo puede tener una muy baja pertenencia de 0.1 al grupo de los bajos.
Clasifique a las personas de acuerdo con su estatura en dos conjuntos


oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Universo de discurso
Todas las personas pertenecen en cierta medida a ambos conjuntos.
La totalidad de los elementos que se estan clasificando, se puede escoger esa totalidad o todo el mundo.
En este escenario representaría los números reales que representen las estaturas de las personas.
Conceptos básicos

oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Función de membresía
Medida de pertenencia de un elemento al conjunto
0 significa no hay pertenencia al conjunto y 1 significa que hay mucha pertenencia
Conceptos básicos


Bajos
Altos
oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Función de membresía para el conjunto de los bajos
La altura intermedia entre 1 y 2.5 es 1.75
Estaturas inferiores a 1.75 decrecen pertenencia y superiores a 1.75 incrementan pertenencia aproximándose a 1.
Conceptos básicos


oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
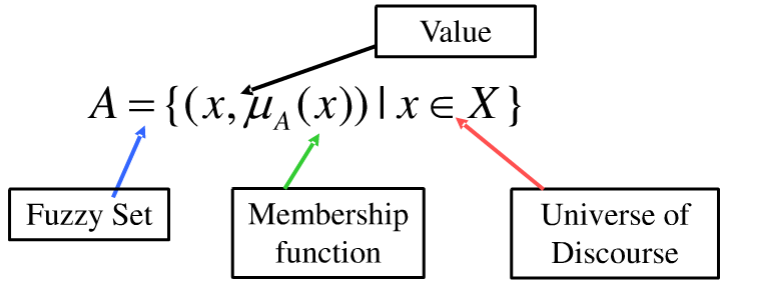
Asumamos que X es la colección de objetos representado por x, un conjunto difuso A en X es un conjunto de pares ordenados.
Entre mayor sea el valor de su funcion de membresia, mayor sera la certeza de que x pertenece a A.
Notación de los conjuntos difusos
oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Los miembros del conjunto difuso tienen un grado de pertenencia o membresía.
Un conjunto difuso puede ser representado por un conjunto de pares ordenados, el primer elemento es ensimmismo el elemento, el segundo elemento es el grado de pertenencia-membresia.
Representación pares ordenados

oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Un agente de bienes raíces quiere clasificar las casas que ofrece a sus clientes. Un indicador de la comodidad de las casas es el numero de habitaciones en ellas.
Definiendo X={1,2,3,4...,10} como el conjunto de casas disponibles. El conjunto difuso de "comodidad de acuerdo al tipo de casa para una familia" puede ser descrito de la siguiente manera:
Ejemplo de estudio de conjuntos difusos

oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Representación como la unión de sus elementos (Conjuntos difusos discretos)



Función de membresía
oscarrosete.com
oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Representación como la unión de sus elementos (Conjuntos difusos continuos)
Función de membresía


oscarrosete.com

oscarrosete.com
Agenda
2.1. Introducción a la Lógica Difusa
2.2. Conjuntos difusos y funciones de membresía
2.3. Operaciones sobre conjuntos difusos
2.4. Inferencia usando Lógica Difusa
2.5. Diseño de clasificadores difusos
Unidad 2: Lógica Difusa Tipo – I
oscarrosete.com
oscarrosete.com
Conjuntos clásicos
B es un subconjunto de A, porque todos sus elementos están contenidos en A.
Si solo parcialmente algunos de B están en A, entonces B no es un subconjunto de A.


oscarrosete.com
oscarrosete.com
Conjuntos difusos
Tenemos que realizar alguna operación u evaluación con respecto a funciones de membresía, ya que caracterizan la pertenencia de los elementos a los conjuntos difusos.


oscarrosete.com
oscarrosete.com
Conjuntos difusos
El conjunto difuso B es subconjunto del conjunto difuso A si y solo si la función de membresía de B es menor o igual a la función de membresía de A para todos los posibles valores en el universo de discurso X.


oscarrosete.com
oscarrosete.com
Conjuntos Certeros
La intersección sera definida como todos los elementos que estén en A y B.
¿Cómo lo generalizamos para conjuntos difusos, si todos los elementos tienen cierta pertenencia a todos los conjuntos?


oscarrosete.com
oscarrosete.com
Conjuntos Difusos
La intersección sera definida como todos los elementos que estén en A y B.




oscarrosete.com
oscarrosete.com
Conjuntos Certeros
La unión sera definida como todos los elementos que estén en A ó en B.


oscarrosete.com
oscarrosete.com
Conjuntos Difusos
La unión sera definida como todos los elementos que estén en A ó en B.

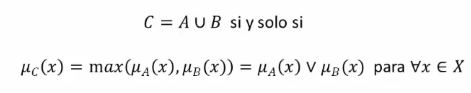


oscarrosete.com
oscarrosete.com
Conjuntos Certeros
El complemento sera definido como todos los elementos que estén en X, pero no en A


oscarrosete.com
oscarrosete.com
Conjuntos Difusos

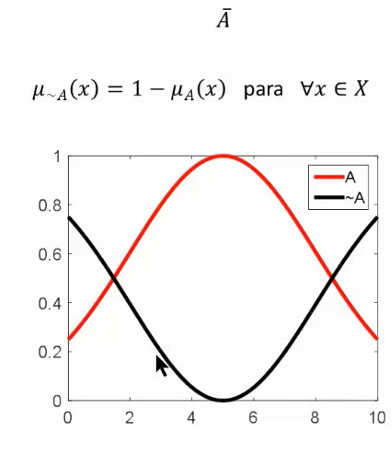
El complemento sera definido como todos los elementos que estén en X, pero no en A


oscarrosete.com
oscarrosete.com
Ejercicios independientes
Dados los siguientes conjuntos difusos determine
- Intersección
- Unión
- Complemento de A
- Complemento de B
Represente gráficamente su resultado



Ejercicio 2
Ejercicio 1
Universo de discurso=X={5,10,20,25,30,40}

oscarrosete.com
oscarrosete.com
Propiedades fundamentales de los conjuntos clasicos

Fundamental properties of crisp set operations
Conmutativa
Asociativa
Distributiva
Idempotencia
Identidad
Involutiva
Leyes de morgan

oscarrosete.com
oscarrosete.com
Propiedades fundamentales de los conjuntos clasicos


oscarrosete.com
oscarrosete.com
Propiedades fundamentales de los conjuntos difusos


oscarrosete.com
oscarrosete.com
Resumen básico
Un conjunto es una colección de elementos con cierta propiedad


1(verdadero)
0(falso)

Conjunto difuso: conjunto con membresía graduada


oscarrosete.com
oscarrosete.com
Resumen básico
Conjunto Difuso: Conjunto con membresía graduada

oscarrosete.com
oscarrosete.com
Resumen básico
Conjunto Difuso: Conjunto con membresía graduada
Subjetivo y dependiente del contexto

oscarrosete.com
oscarrosete.com
Variable linguística
Es una variable cuyos posibles valores son palabras y pueden ser representados mediante conjuntos difusos.
Todos los valores linguistico forman un conjunto de terminos o etiquetas denominados terminos linguisticos.
Permite describir el estado de un objeto o fenómeno.

Funciones de membresía
oscarrosete.com
oscarrosete.com
Variable linguística

oscarrosete.com
oscarrosete.com
Variable linguística
Una variable lingüística se caracteriza mediante
- v es el nombre de variable
- X es el universo de discurso de la variable v
- T es el conjunto de términos lingüísticos de v
- regla sintáctica para generar los términos lingüísticos
- regla semántica para asignar a cada termino un significado, que es un conjunto difuso en X
oscarrosete.com
oscarrosete.com
Propiedades fundamentales de los conjuntos difusos

Todas las propiedades para conjuntos clásicos son válidas para los difusos, excepto la complementareidad.
oscarrosete.com
oscarrosete.com
Potencial de lógica difusa
Semana 12 (19-23 de Abril)
presentación de proyectos lógica difusa
Fuzzy-logic classifier/controller

oscarrosete.com

oscarrosete.com
Agenda
2.1. Introducción a la Lógica Difusa
2.2. Conjuntos difusos y funciones de membresía
2.3. Operaciones sobre conjuntos difusos
2.4. Inferencia usando Lógica Difusa
2.5. Diseño de clasificadores difusos
Unidad 2: Lógica Difusa Tipo – I
oscarrosete.com
oscarrosete.com
Potencial de lógica difusa


oscarrosete.com
oscarrosete.com
Ejercicios independientes (python)
Dados los siguientes conjuntos difusos determine
- Intersección
- Unión
- Complemento de A
- Complemento de B
Represente gráficamente su resultado



Ejercicio 2
Ejercicio 1
Universo de discurso=X={5,10,20,25,30,40}


oscarrosete.com
oscarrosete.com
Propiedades fundamentales de los conjuntos difusos

Todas las propiedades para conjuntos clásicos son válidas para los difusos, excepto la complementareidad.

oscarrosete.com
oscarrosete.com
Variable linguística
Es una variable cuyos posibles valores son palabras y pueden ser representados mediante conjuntos difusos.
Todos los valores linguístico forman un conjunto de términos o etiquetas denominados términos linguísticos.
Permite describir el estado de un objeto o fenómeno.

Funciones de membresía

oscarrosete.com
oscarrosete.com
Funciones membresía
La principal diferencia existente entre los conjuntos difusos y los clásicos o certeros es la posibilidad de asignar valores de pertenencia entre 0 y 1 a los elementos del universo de discurso.
La relación entre el valor de membresía a un conjunto difuso y los elementos es denominada como función de membresía.



oscarrosete.com
oscarrosete.com
Terminología relacionada a las funciones de membresía
El núcleo de una función de membresía para un conjunto difuso es la región del universo caracterizada por tener pertenencia total al conjunto (valor de 1).
Las fronteras son las regiones donde los elementos tienen valores de membresía entre 0 y 1.


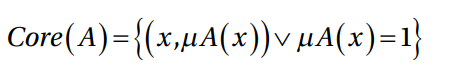
oscarrosete.com
oscarrosete.com
Terminología relacionada
El soporte de una función de membresía para un conjunto difuso se define como la región del universo caracterizada por tener un valor de membresía diferente de 0.
La unión de núcleo y frontera nos da el soporte.


oscarrosete.com
oscarrosete.com
Puntos de cruce, elementos en el universo para los cuales su valor de membresía es igual a 0.5.



Terminología relacionada
oscarrosete.com
oscarrosete.com
El ancho de banda es definido como el valor absoluto de la diferencia de los puntos de cruce.


Terminología relacionada

oscarrosete.com
oscarrosete.com
Clasificaciones de funciones de membresía
Un conjunto difuso normal es el que cuenta con una función de membresía que tiene por lo menos un elemento x en el universo cuyo valor de membresía es unitario.
Si tiene núcleo un conjunto y no es vacío, el conjunto será normal.


oscarrosete.com
oscarrosete.com
La función roja y azul alcanza por lo menos en 1 punto el valor de 1.
Azul y roja funciones normales, función verde subnormal.
Deseamos crear y diseñar funciones de membresía normales

oscarrosete.com
oscarrosete.com
Normality


oscarrosete.com
oscarrosete.com
Si una función de membresía de un conjunto difuso A satisface el siguiente criterio en un punto c, se le denomina un conjunto simétrico.



Clasificaciones de funciones de membresía
oscarrosete.com
oscarrosete.com
Symmetry
Verde es una función de membresía simétrica
Azul y roja no son simétricas, la roja tiene inclinación distinta de un lado con respecto al otro y ambas no se encuentran centradas.
se diseñan simétricas para simplificar proceso de diseño.


oscarrosete.com
oscarrosete.com
Las funciones de membresía pueden ser abiertas por la derecha, abierta por la izquierda o cerradas

Clasificaciones de funciones de membresía


Open left

Open right

Closed
oscarrosete.com
oscarrosete.com
Las funciones abiertas por la derecha, nunca baja el valor de membresía hacia 0.
No hay prioridad en el diseño, generalmente se diseñan abiertos los conjuntos de los extremos del universo y cerrados en el centro.


Abiertas vs Cerradas
oscarrosete.com
oscarrosete.com
Un conjunto difuso convexo es descrito por una función de membresía cuyos valores son monotónicamente incrementales o monotónicamente decrementales para valores incrementales de los elementos del universo.
Debe cumplir con la siguiente regla.

Clasificaciones de funciones de membresía

oscarrosete.com
- Seleccionamos valores x1 y x2
- Encontramos valores de membresía para esos dos elementos.
- Todos los valores de membresía en ese rango tienen que ser al menos igual que el mínimo de esos dos valores de membresía.


Convexas vs no convexas
oscarrosete.com
Función en verde y rojo son convexas, la azul no

oscarrosete.com
oscarrosete.com
Formas especiales de F. de membresía
Si un conjunto difuso solo tiene un único punto, teniendo un valor de membresía de 1, es considerado un conjunto singleton (Fuzzy Singleton)



oscarrosete.com
oscarrosete.com
Formas especiales de F. de membresía
A los controladores difusos solo le llegan valores discretos en algún momento del tiempo, los representamos como singleton.



oscarrosete.com
oscarrosete.com
Formas especiales de F. de membresía
Conjunto cortado, conjunto clásico resultado de cortar un conjunto difuso.
Un conjunto cortado (α– Cut) es un conjunto que contiene todos los elementos con los valores de membresía mayores o iguales a α.


oscarrosete.com
oscarrosete.com
Formas especiales de F. de membresía
Se utiliza para transformar los conjuntos difusos que son resultados de los controladores difusos a un resultado certero.


oscarrosete.com
oscarrosete.com
Funciones de membresía típicas
Consideremos un tiro de penales en futbol soccer.
En términos discretos un tiro puede ser 1 (patada completa) o 0 (no patada).
En la vida real, esto no sucede, la velocidad del tiro depende no solo de la mente del tirador, sino de la anticipación de hacia donde se dirigirá el guardameta.
El tirador selecciona la velocidad de la patada y la dirección a la que apunta.


oscarrosete.com
oscarrosete.com
Funciones de membresía típicas
La velocidad no puede ser definida únicamente con dos valores discretos, 0 y 1. La velocidad varia entre 0 y 1; 0 consistiendo en velocidad nula y 1 velocidad maxima.
Supongamos que el tirador apunta a la esquina superior derecha, en esta situación la decision principal consistirá en seleccionar la velocidad más adecuada.
Mucha velocidad elevaría demasiado la pelota, muy lento puede ser anticipado.


oscarrosete.com
oscarrosete.com
Funciones de membresía típicas
Derivadas discontinuas
Derivadas discontinuas: la pendiente sufre cambios abruptos en algunos puntos del universo de discurso.
Función triangular, así como un triangulo tiene 3 coordenadas, la función de membresía triangular tiene 3 parámetros.
El núcleo es un solo elemento (b).




oscarrosete.com
oscarrosete.com
Función triangular
Supongamos que el tirador puede seleccionar 4 tipos de tiros:
- Tiro directo de alta velocidad
- Tiro curvo de potencia media
- Tiro directo lento
- Tiro directo hacia la izquierda de potencia media.


oscarrosete.com
Función triangular
En promedio la velocidad media de un tirador de penales es de 80 mph, por lo tanto no hay manera de decir que esa velocidad es lenta.
Asignamos 0% de valor de membresía a 80 mph en el conjunto difuso de velocidad lenta.
Similar, de manera arbitraria, una velocidad 60 mph puede ser considerada 70% rápida y 30% media.

oscarrosete.com
Función triangular
Considerando los tres parámetros de la función triangular.
- Tiro directo de alta velocidad [60,80,80]
- Tiro curvo de potencia media [30,50,70]
- Tiro directo lento [20,20,45]
- Tiro directo hacia la izquierda de potencia media [50,60,80]

oscarrosete.com


oscarrosete.com
oscarrosete.com
Función Trapezoidal, así como un trapezoide tiene cuatro coordenadas, una función de membresía trapezoidal tiene 4 valores. a, b, c y d.



Funciones de membresía típicas
Derivadas discontinuas
oscarrosete.com
oscarrosete.com
Los valores de membresía comienzan a subir en la primer frontera (entre a y b), y baja a cero en la segunda frontera (entre c y d).
Comparada con la función triangular tiene un núcleo mas amplio que va entre b y c.


Cerrada
Abierta por la derecha
Función trapezoidal
oscarrosete.com
oscarrosete.com

Función trapezoidal
Considerando los cuatro parámetros de la función trapezoidal.
- Tiro directo de alta velocidad [60, 80, 80, 90]
- Tiro curvo de potencia media [30,50,50,70]
- Tiro directo lento [20,30,30,50]
- Tiro directo hacia la izquierda de potencia media [50,60,60,80]

oscarrosete.com
oscarrosete.com
Ejercicio alumno
Grafique funciones de membresía para el ejemplo mencionado en clase.
Sin utilizar librería skfuzzy
- Triangular
- Trapezoidal
Utilizando librería skfuzzy, represente los conjuntos difusos previamente mencionados utilizando:
- Campana generalizada
- Función gaussiana
- Función sigmoidal

oscarrosete.com
oscarrosete.com
Funciones de membresía típicas
Derivada continua, funciones cerradas simétricas
Cuando se conoce la media aritmética y la desviación estándar de los valores certeros y los queremos tomar en cuenta en la representación difusa, se puede utilizar una función de membresía Gaussiana.
c es la media aritmética, s la desviación estándar y m es el factor de fuzzificación.


oscarrosete.com
oscarrosete.com
Función Gausiana
La función gaussiana es similar a la función triangular pero con derivada continua.


oscarrosete.com
oscarrosete.com
Función Gausiana
Al aplicar la función de membresía al ejemplo de soccer la representación cuenta con mejoría y la interpolación es más suave.
Ejemplo considerando distribución de datos históricos y que cuentan con una desviación estándar de 4 mph.
Podríamos asignar a la velocidad máxima una media de 80 mph y generar las siguientes funciones gaussianas de manera similar.

oscarrosete.com
oscarrosete.com
Función Gausiana
- Tiro directo de alta velocidad [x, 80, 4]
- Tiro curvo de potencia media [x,50,4]
- Tiro directo lento [x,30]
- Tiro directo hacia la izquierda de potencia media [x,60,4]


oscarrosete.com
oscarrosete.com
La función de membresía de campana generalizada toma en consideración 3 parametros:
- La pendiente
- El centro
- El ancho de la curva
Se representa por la siguiente ecuación

Funciones de membresía típicas
Derivada continua, funciones cerradas simétricas

oscarrosete.com
oscarrosete.com
Se relaciona con la función trapezoidal, pero cuenta con derivada continua.



Función campana generalizada

oscarrosete.com
oscarrosete.com
Para representar una función abierta con derivada continua utilizamos la función sigmoidal.
La transición entre valor de membresía de 0 y valor de membresía de 1 es definida por a.
Punto de cruce es donde vale 0.5 el valor de membresía



Funciones de membresía típicas
Derivada continua, función abierta

oscarrosete.com
oscarrosete.com
Ver la distribución de los datos, por ejemplo con ayuda de un histograma. Si no se pueden deducir patrones de la visualización se recomienda utilizar función triangular o trapezoidal, en caso contrario utilizar funciones basadas en la distribución.
Entrenar el modelo con funciones de membresía distintas y comparar los resultados utilizando métricas tales como MAPE (mean average percentage error), el método que te de el menor error es el mejor modelo.
Recomendaciones

oscarrosete.com
oscarrosete.com
Otras opciones
Funciones de membresia polinomiales




z-shaped
s-shaped
pi-shaped
oscarrosete.com
oscarrosete.com
Agenda
- Logica clasica vs logica difusa
- Variable lingüística
- Reglas si-entonces
- Modus Ponens Difuso
Razonamiento aproximado

oscarrosete.com
oscarrosete.com
Lógica clásica
La lógica formal se enfoca al desarrollo de esquemas de razonamiento válidos en cuanto al proceso con que se deducen las conclusiones en función de las premisas, sin atender al contenido de los enunciados, o mas propiamente proposiciones, ambos conceptos entendidos en el único sentido de expresiones lingüísticas que puedan ser verdaderas o falsas.
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
Estudia la naturaleza del lenguaje y sus relaciones independiente de la realidad del mundo, tiene como utilidad infinitas aplicaciones entre las cuales los circuitos lógicos de la electrónica se encuentran.
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
La lógica analiza la forma del pensamiento para determinar argumentos o razonamientos válidos e inválidos con el uso de reglas y técnicas, además proporciona leyes y principios que otorgan un mayor conocimiento verídico y preciso.
La lógica se utiliza en la cotidianidad, ya que a través de acciones diarias hacemos uso de esta para tomar decisiones o ejecutar alguna acción.
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
El razonamiento lógico es un proceso mental mediante el cual los seres humanos obtienen conclusiones a partir de hipótesis consideradas como verdaderas.
Razonamiento intuitivo, deductivo, inductivo, por analogía
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
Ejemplos
Todo hombre es mortal. Sócrates es hombre. Por lo tanto, Sócrates es mortal.
Arturo observa el cielo oscuro en la ciudad de Mexicali a las 2:00 p.m
Arturo concluye: !va a llover!
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
Proposición clásica
En lógica matemática, una proposición es una afirmación con sentido completo y en un contexto específico de la que se puede determinar si es verdadera(1) o falsa(0).
Ejemplos
- 5 es un número par
- Júpiter es un planeta.
- Colombia es un país suramericano
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
Proposición clásica
Bertrand Russell propuso el término de proposiciones atómicas a los elementos más simples que componen un razonamiento, describe un hecho, afirma que una cosa posee una cualidad o determina la relación entre dos hechos o cosas y proposiciones moleculares aquellos enunciados que describen un conjunto de hechos o un estado complejo de cosas.
También llamadas simples y compuestas.
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
Términos de enlace y conectivos lógicos
Los términos de enlace se usan para crear y formar proposiciones a partir de proposiciones simples.
Los términos de enlace son "y", "o", etc.
Lógica clásica vs lógica difusa


oscarrosete.com
oscarrosete.com
Ejemplos
La Tierra no es cuadrada
Es una proposición compuesta que utiliza el término de enlace "no", el cual actua sobre una proposición simple, "La Tierra es cuadrada"
Hace sol o hace frío
El termino de enlace "o", actúa sobre las proposiciones simples "Hace sol" y "Hace frio"
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
Simbolización de proposiciones
Las proposiciones simples se simbolizan con las letras del alfabeto p,q,r,s
p: los habitantes de Marte invaden la tierra.
q: los directivos son amables con sus subordinados
r: El gobierno regula la inflación.
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
Simbolización de proposiciones
Las proposiciones compuestas se simbolizan utilizando letras proposicionales entre paréntesis, para distinguir las proposiciones simples entre sí, y conectivos lógicos.
Lógica clásica vs lógica difusa


oscarrosete.com
oscarrosete.com
Simbolización de proposiciones
La siguiente tabla muestra algunas frases que representan los conectivos lógicos:
Lógica clásica vs lógica difusa


oscarrosete.com
oscarrosete.com
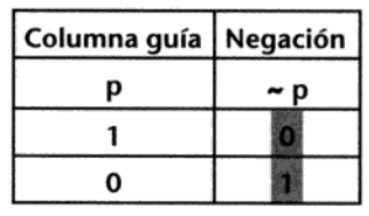
Tabla de valores de verdad para los diferentes conectivos
Una tabla de verdad es un esquema que muestra todas las combinaciones que puede haber en un argumento según sus variables involucradas.
Permite visualizar las combinaciones de valores de verdad que se les da a las proposiciones.
Lógica clásica vs lógica difusa


oscarrosete.com
oscarrosete.com
Traducción del lenguaje natural al simbólico
1. Se le asigna una letra siempre diferente a cada enunciado
2. Se simboliza cada idea del argumento y se agrupan dichas ideas partiendo de (),[] y {}. Cada idea del argumento se une con una conjunción.
3. Todo argumento tiene un conector principal y este separa la conclusión de las premisas.
Como paso adicional se puede determinar
el valor de verdad de la proposición compuesta.
Lógica clásica vs lógica difusa

oscarrosete.com
oscarrosete.com
Ejemplo
Mi tío no vino a dormir y no fue a trabajar
1. Asignamos variables proposicionales.
Dicha proposición esta compuesta por las proposiciones simples:
p: Mi tío no vino a dormir
q: Mi tío no fue a trabajar
2. Traducción lógica
Lógica clásica vs lógica difusa


oscarrosete.com
oscarrosete.com
Ejemplo
3. Obtener la cantidad de combinaciones de valores de verdad, dos variables proposicionales por lo que la cantidad de combinaciones de valores de verdad será:
2^2=4.
4. Asignar valores de verdad a variables y resolver operaciones lógicas.
Lógica clásica vs lógica difusa


oscarrosete.com
oscarrosete.com
Base de los conectivos lógicos
Lógica clásica vs lógica difusa



oscarrosete.com
oscarrosete.com
Hay 3 operaciones elementales a partir de las cuales las demas pueden obtenerse.
conjuncion, disyuncion y negacion.
Ejemplo
Implicación, negamos antecedente p y hacemos la disyunción con el consecuente.
Lógica clásica vs lógica difusa



oscarrosete.com
oscarrosete.com
Proposición difusa
Sentencia cuya veracidad puede tomar valores entre 0 y 1.


Lógica proposicional (difusa)
oscarrosete.com
oscarrosete.com
Generalización a lógica difusa
Nota: La conjunción se da entre valores de veracidad, no valores de membresía



Lógica proposicional (difusa)
oscarrosete.com
oscarrosete.com
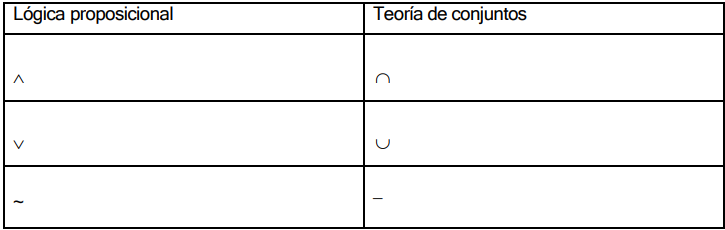
Correspondencia con operadores de teoría de conjuntos

Lógica proposicional (difusa)
oscarrosete.com
oscarrosete.com
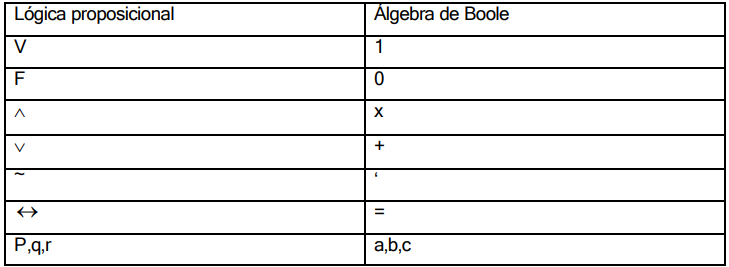
Correspondencia con Álgebra de Boole

Lógica proposicional (difusa)
oscarrosete.com
oscarrosete.com
Una tautología se define como una proposición formada por la combinación de otras proposiciones y cuya verdad es independiente de la certeza o falsedad de las proposiciones que la forman.
En la lógica clásica el Modus Ponendo Ponens y Modus Tollendo Tollens son tautología.

Lógica proposicional (difusa)
oscarrosete.com
oscarrosete.com

Lógica proposicional (difusa)
Inferencia lógica
Es una parte primordial de la logica formal que se centra en el analisis de los razonamientos correctos. Para la inferencia logica, la validez de un razonamiento esta determinada por su forma logica, independientemente de la realidad del mundo.
En la teoria clasica proposicional existen dos importantes reglas de inferencia, el Modus Tollens y el Modus Ponens.
oscarrosete.com
oscarrosete.com

Lógica proposicional (difusa)
Modus Ponendo Ponens (MPP)
En latín significa "modo en que afirmando se afirma". De la afirmación del antecedente se infiere la afirmación del consecuente.
Premisa 1: "x es A"
Premisa 2: "Si x es A, entonces y es B"
Consecuencia:" Y es B"


oscarrosete.com
oscarrosete.com

Lógica proposicional (difusa)
Ejemplos


oscarrosete.com
oscarrosete.com

Lógica proposicional (difusa)
El Modus Tollendo Tollens(MTT)
En latín significa "modo en que negando se niega"
De la negación del consecuente se infiere la negación del antecedente.
Premisa 1: "y es No B"
Premisa 2: "SI X es A Entonces y es B"
Consecuencia: "x es no A"


oscarrosete.com
oscarrosete.com

Lógica proposicional (difusa)
Ejemplos



oscarrosete.com
oscarrosete.com
Ejercicio: Considere que V(p)=0.3, V(q)=0.8 y V(s)=0.5 para calcular el grado de verdad de las siguientes proposiciones compuestas:


Lógica proposicional (difusa)
oscarrosete.com
oscarrosete.com
Un sistema de inferencia difusa

Sistemas de Inferencia Difusa
El esquema de un sistema basado en técnicas de lógica difusa se presenta en la figura
oscarrosete.com
oscarrosete.com
Un sistema de inferencia difusa

Sistemas de Inferencia Difusa
Esta compuesto por los siguientes bloques
Bloque difuso: bloque en el que a cada variable de entrada se le asigna un grado de pertenencia a cada uno de los conjuntos difusos. Las entradas a este bloque son valores concretos de las variables de entrada y las salidas son grados de pertenencia a los conjuntos difusos considerados.
oscarrosete.com
oscarrosete.com
Un sistema de inferencia difusa

Sistemas de Inferencia Difusa
Bloque de inferencia:
Bloque que, mediante los mecanismos de inferencia relaciona conjuntos difusos de entrada y de salida y que representa a las reglas que definen el sistema. Las entradas a este bloque son conjuntos difusos(grados de pertenencia) y las salidas son también conjuntos difusos, asociados a la variable de salida.
oscarrosete.com
oscarrosete.com
Un sistema de inferencia difusa

Sistemas de Inferencia Difusa
Desdifusor:
Bloque en el cual a partir del conjunto difuso obtenido en el mecanismo de inferencia y mediatne los metodos matematicos de desdifusion se obtiene un valor concreto de la variable de salida, es decir, el resultado.
oscarrosete.com
oscarrosete.com
Un sistema de inferencia difusa provee una manera de "mapear" un espacio de entradas a un espacio de salidas con lógica difusa. Un FIS intenta emular el proceso con el que los humanos razonamos, utilizando lógica difusa especialmente las reglas si-entonces.

Sistemas de Inferencia Difusa

oscarrosete.com
oscarrosete.com
Los bloques previamente mostrados se describen como:
- Una base de datos con todas las reglas SI-Entonces describiendo el sistema
- Una base de datos con las funciones de membresía
- operaciones de inferencia en las reglas difusas
- Defuzzificacion de los resultados en salidas certeras.
A la unión de las reglas y funciones de membresía se les llama base del conocimiento.

Sistemas de Inferencia Difusa
oscarrosete.com
oscarrosete.com
Los sistemas de inferencia difusos pueden ser divididos en tres tipos:
- Modelo Mamdani
- Modelo Takagi-Sugeno
- Modelo Tsukamoto

Sistemas de Inferencia Difusa
oscarrosete.com
oscarrosete.com
Modelo Mamdami

Sistemas de Inferencia Difusa
Es el modelo mas ampliamante utilizado por su estructura simple, es utilizado para resolver problemas de toma de decisión generales.

oscarrosete.com
oscarrosete.com
Fuzzification

Sistemas de Inferencia Difusa
convertir entradas certeras en conjuntos difusos
Supongamos en nuestra base de reglas tenemos la siguiente:
Podemos dividir la critica de los productos y la belleza del producto en una calificación del 1 al 5.

oscarrosete.com
oscarrosete.com
Fuzzification (sigmoidal)

Sistemas de Inferencia Difusa



Excellent reviews
Awesome product
oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Suponiendo critica de 1 y una entrada de nuestro diseño equivalente a 4

Find and evaluate the antecedent
oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Considerando la condición OR, podemos aplicar un operador de maximización.
max(0.0, 0.7)=0.7
Find the consequent

oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Suponiendo la función de membresía del consecuente también es sigmoidal y la regla menciona:
Find the consequent


oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Suponiendo tenemos las siguientes tres reglas en nuestra base de reglas y las funciones de membresía de salida son triangulares y analizamos una critica=1 y un diseño=4.
Aggregate the consequents

oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Aggregate the consequents

oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Aggregate the consequents
Una vez evaluadas todas las reglas y obtenidos los conjuntos difusos de salida modificados, hay que realizar la agregacion de todas las reglas para obtener un resultado unico de la actuacion de todas ellas.
Esta agregación es una unión lógica y una vez más para conservar la equivalencia entre lógicas clásica y difusa se traduce por una t-conorma.
oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Aggregate the consequents

oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Defuzzify the results
El bloque desdifusor realiza la función contraria al difusor. El difusor tiene como entradas valores concretos de las variables de entrada y como salidas grados de pertenencia a conjuntos difusos. La entrada al bloque desdifusor es el conjunto difuso de salida, resultado del bloque de inferencia y la salida es un valor concreto de la variable de salida.
Ejemplos sencillos de métodos de calculo son:
- Método del máximo
- Método del centroide
- Método de la altura
oscarrosete.com
oscarrosete.com

Sistemas de Inferencia Difusa
Defuzzify the results
Método del centroide
Utiliza como salida del sistema el centro de gravedad de la función característica de salida
Es el método mas utilizada en aplicaciones de la lógica difusa a la ingeniería ya que se obtiene una solución única , aunque a veces es difícil de calcular.
Con esta formula obtendríamos un resultado
de 13.75%
oscarrosete.com
oscarrosete.com
Sistemas de Inferencia Difusa
Aplicación
oscarrosete.com
oscarrosete.com
La variable lingüística cuenta con 5 elementos
- x es su nombre
- X es su universo de discurso
- T(x) los valores lingüísticos o términos lingüísticos que acepta la variable
- G es la regla sintáctica que genera los valores lingüísticos.
- M es la regla semántica que asocia cada termino lingüístico con su significado
Los términos lingüísticos describen cualitativamente la variable lingüística.
Razonamiento aproximado

oscarrosete.com
oscarrosete.com
Ejemplo
x= posesión del balón
X=[0,90] minutos
T(x)={casi nada, poca,
equilibrada, grande,
enorme}
son propuestas, pudo centrar
gaussianas distintas
Razonamiento aproximado



La cantidad de terminos linguisticos y su selección se hará a la conveniencia del diseñador.
oscarrosete.com
oscarrosete.com
Nosotros tenemos libertad de elegir conjuntos difusos y sus funciones de membresía para cada uno de los términos lingüísticos siempre y cuando sean razonables
Razonamiento aproximado


oscarrosete.com
oscarrosete.com
Son el núcleo de un controlador difuso
si x es A, entonces y es B
relacion entre si ocurre algo concluimos que ocurre otra cosa
Donde x y y son variables linguisticas
A y B son valores o terminos linguisticos
si la presion es alta, entonces el volumen es grande
si la carretera es sinuosa, entonces la carretera es peligrosa
si el jitomate esta rojo, entonces el jitomate esta maduro
Reglas Difusas SI-Entonces

oscarrosete.com
los terminos linguistiocs tienen un significadod deifinido por un conjunto difuso
un ser humano las puede entender estas reglas, la idea es que una computadora la pueda utilizar para concluir cosas, concluir razonamientos, debe tener una manera de interpretar estas reglas si entonces de manera matematica
Reglas Difusas SI-Entonces


oscarrosete.com
oscarrosete.com
Existen dos maneras de interpretar las reglas si entonces de manera matematica
la relacion difusa formada por el producto cartesiana entre el conjunto a yb
la otra es utilizar la implicacion difusa.
Las dos tienen interpretaciones distintas.
Reglas Difusas SI-Entonces

oscarrosete.com

oscarrosete.com
Relación difusa AXB
intensidad de la causabilidad entre A y B, cuando tiene una calificacion arriba de 8, la intensidad de la relacion con estudiar mucho es mas grande.
intensidad de la relacion del antecedente si entonces con el consecuente de la misma regla
Reglas Difusas SI-Entonces

oscarrosete.com


oscarrosete.com
La veracidad de la implicacion
a implica a b
para que sea falsa la implicacion el antecedente sea verdadero y el consecuente sea falso.
azul es igual a cero
Reglas Difusas SI-Entonces

oscarrosete.com

oscarrosete.com
Ambas interpretacions son utilizadas, en control difuso se utiliza la interpretación de la relación difuso formada por el producto cartesiando entre A y b
La implicacion para sistemas expertos.
Reglas Difusas SI-Entonces

oscarrosete.com

oscarrosete.com
Se constituye por dos premisas
1 es un hecho
x es una variable linguistica , A' es un termino linguistico
y b
con estas dos premisas podemos obtener una conclusión.
nos permite dar razonamientos utilizando la computadora.
Modus Ponens Difuso

oscarrosete.com
oscarrosete.com
El hecho esta conformado por un conjunto difuso A{
la regla es un producto cartesiano AXB
para la conclusion realizamos la composicion entre el hecho y la regla.
Modus Ponens Difuso

oscarrosete.com

oscarrosete.com
Esta regla si-entonces nos va a servir para concluir que tan excelente es pedro como estudiante.
Modus Ponens Difuso

oscarrosete.com


oscarrosete.com
Modus Ponens Difuso

oscarrosete.com


oscarrosete.com
oscarrosete.com