Automatización y control
Unidad 1: Automatización y Control Industrial
Ing. Oscar Alonso Rosete Beas
Semana 24 Agosto Rev:2 ciclo 2020-2
oscarrosete.com
oscarrosete.com


Agenda
1.1. Definiciones y conceptos relacionados a los sistemas de control
1.2. Aplicaciones industriales de los sistemas de control
1.3. Sistemas de control de lazo abierto y Sistemas de Control de Lazo Cerrado
1.4. Modelado de sistemas dinámicos
Unidad 1: Automatización y Control Industrial
oscarrosete.com
Unidad 1
oscarrosete.com
Pasos recomendados para el diseño de un sistema de control
oscarrosete.com
- Determinar el sistema físico y sus especificaciones.
- Dibujar diagrama de bloques.
- Convertir el sistema físico en un esquemático.
- Desarrollar un modelo matemático y obtener un diagrama de bloques del sistema.
- Reducir el diagrama de bloques.
- Análisis, Diseño y Pruebas.

oscarrosete.com

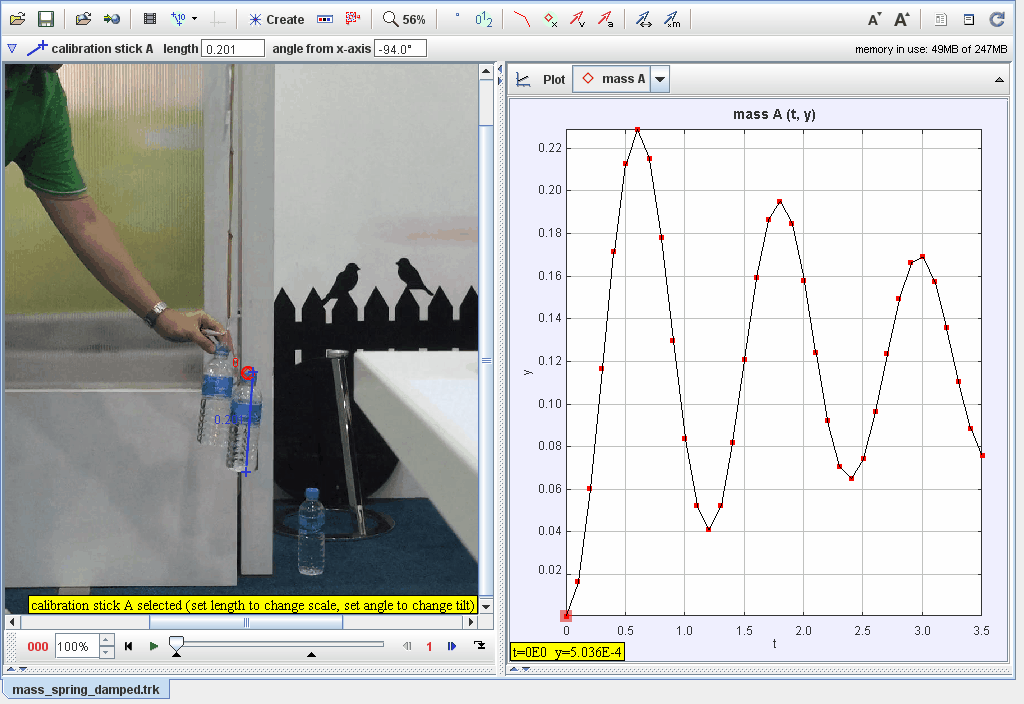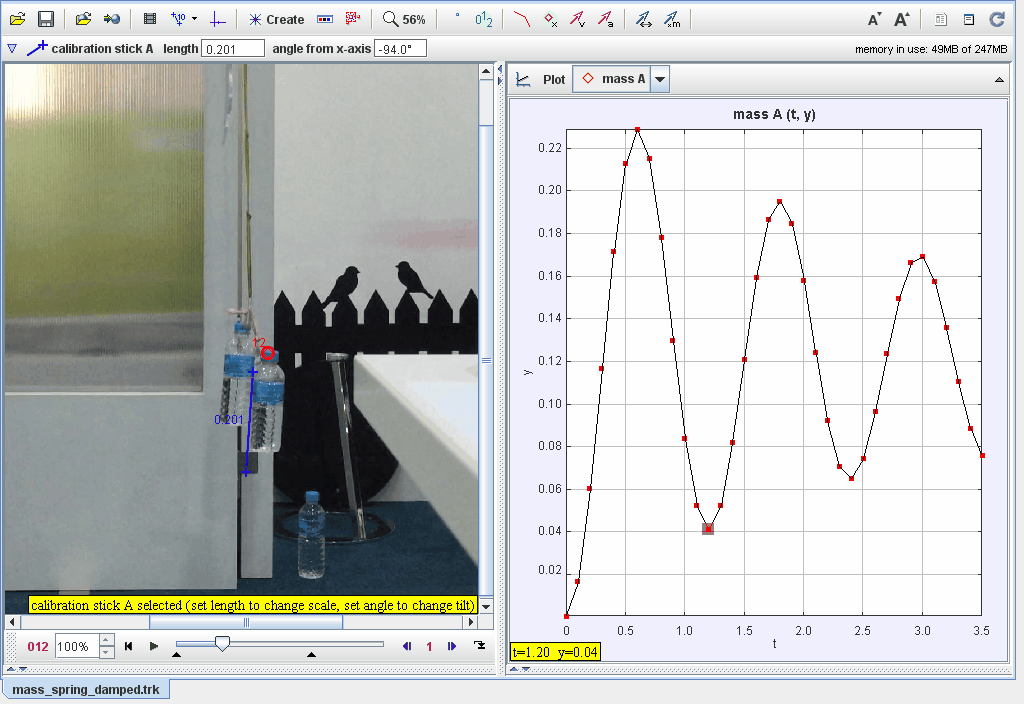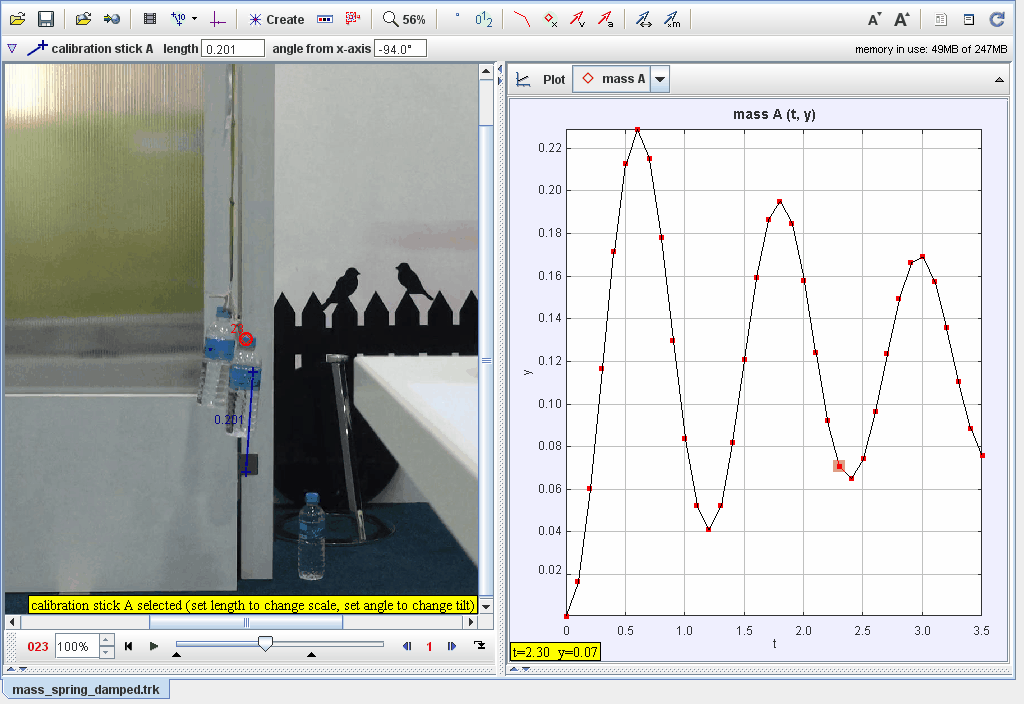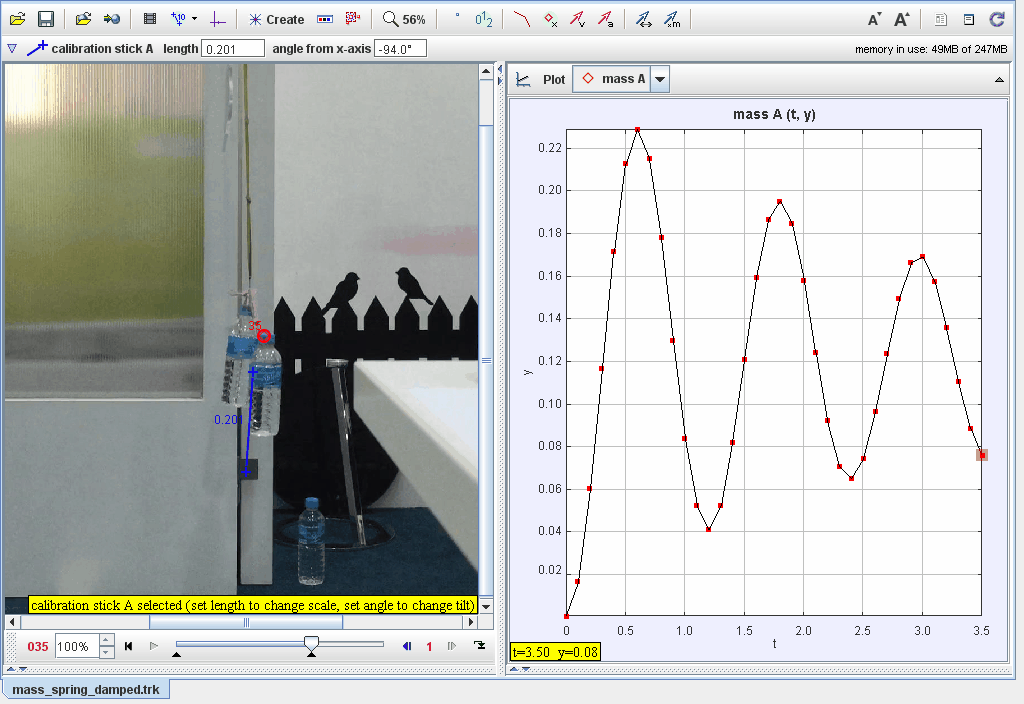
Representación general lazo cerrado
Lazo cerrado
oscarrosete.com
1.4. Modelado de sistemas dinámicos

- Un modelo es una abstracción del mundo físico
- Se utilizan para analizar y diseñar, posiblemente antes de que el sistema físico exista.
- Pueden ser obtenidos de principios físicos o con experimentación.
- El propósito determina el nivel de detalle, suficientemente complejo pero no más de lo necesario.
Un primer principio es un principio básico, una proposición fundamental que como tal no admite demostración a partir de principios más básicos, o no necesita demostración por ser auto-evidente.
- Se utilizan leyes de la física generalmente para derivar modelos.
- Proveen entendimiento.
- Pueden utilizar datos empíricos para determinar parámetros o validar el modelo.
oscarrosete.com
Modelado sistemas dinámicos


Altenativa: Datos Empíricos
- Alimentar el sistema con una entrada conocida y observar la salida, adecuar un modelo a la información recopilada.
- Buenos para sistemas complicados (batería electrolítica, motor de combustión interna)
- Bueno para sistemas "caja-negra" (Reacción conductor)
- No proveen intuición, no pueden ser aplicados en cualquier situación.
oscarrosete.com
Modelado sistemas dinámicos
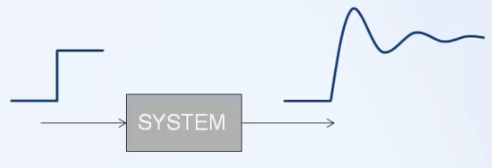
Modelo para diseño/análisis: simple
oscarrosete.com
La complejidad depende del propósito
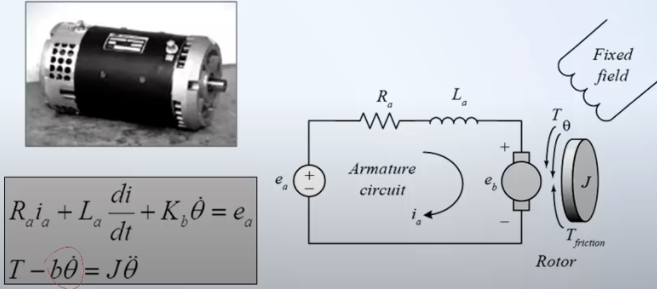
oscarrosete.com
Modelo más preciso simulación
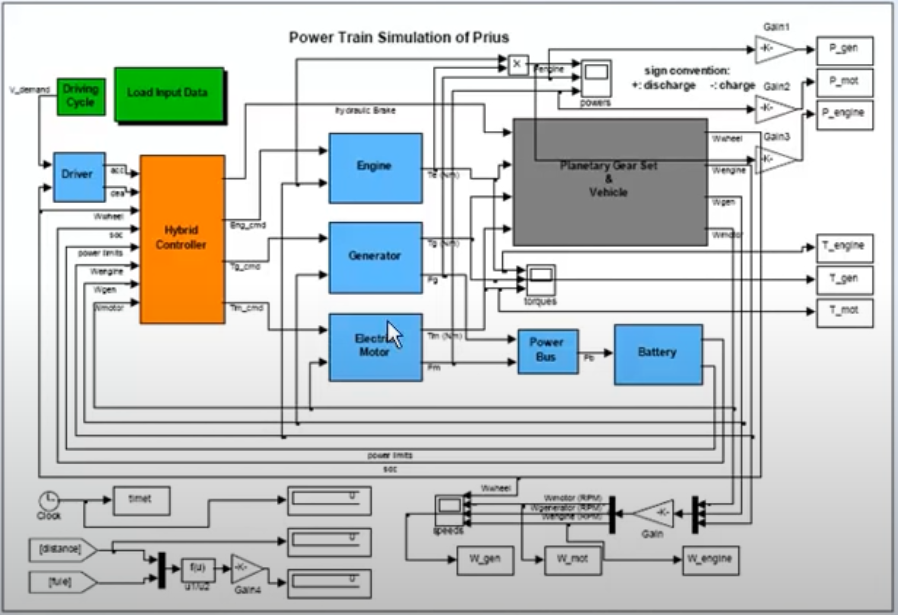
Sistemas estáticos
La salida es determinada únicamente por la entrada actual, reacciona al instante.
La relación I/O no cambia (estática)
Relación representada por ecuación algebraica.
Sistemas estáticos vs dinámicos
Sistemas dinámicos
La salida tiene retardo en su reacción.
La relación I/O cambia con el tiempo y depende de entradas pasadas y condiciones iniciales(dinámico)
Su relación se representa con una ecuación diferencial.
oscarrosete.com
oscarrosete.com
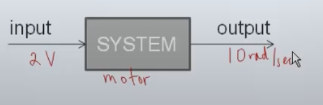
Motor perspectiva estática
Perspectiva dinámica
Sistemas estáticos vs dinámicos
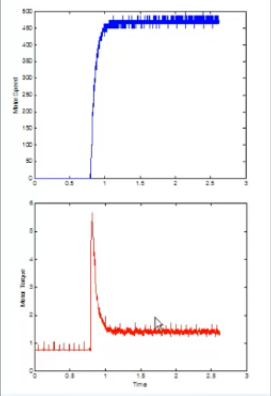
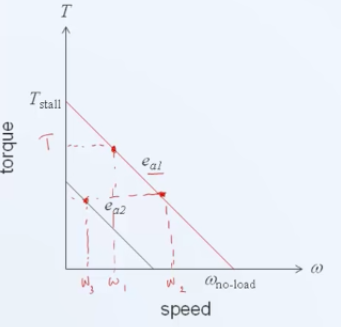
2 enfoques para obtener el modelo de un sistema o proceso
- Primer principio
- Datos empíricos
El nivel de precisión del modelo (model fidelity)
- El detalle y la forma depende del propósito
- Existen desventajas al ser mas complejo
- Estático vs Dinámico
oscarrosete.com
Resumen
La dinámica de un sistema se representa en primer lugar mediante un modelo matemático compuesto por ecuaciones diferenciales.
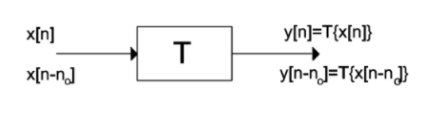
Un sistema LTI (Linear Time-Invariant) es sistema lineal e invariante en el tiempo.
oscarrosete.com
Solución ecuaciones diferenciales LTI
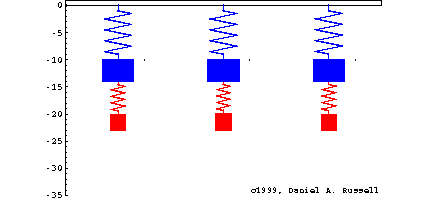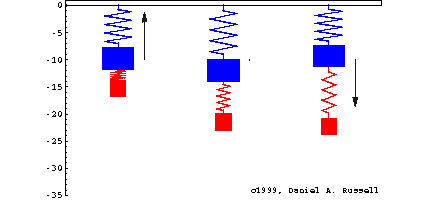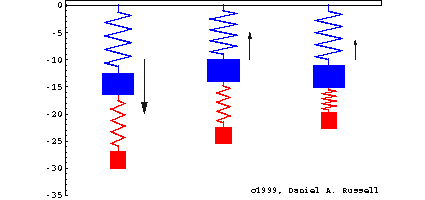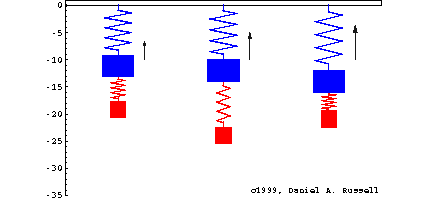
Se caracterizan por cumplir las propiedades siguientes:
- Linealidad: Un sistema es lineal si y solo si podemos aplicar el principio de superposicion.
oscarrosete.com
Solución LTI Differential equations
Se caracterizan por cumplir las propiedades siguientes:
- Invarianza temporal:
si la respuesta del sistema solo depende de T y de la entrada, pero no del instante de tiempo en que se aplica la entrada, se dice que es invariante en el tiempo, o t-invariante.
oscarrosete.com
Solución LTI Differential equations
Los sistemas LTI son muy comunes, incluyen circuitos electricos compuestos por resistencias, inductores y capacitores. Asi como sistemas mecánicos compuestos de masas, resortes y amortiguadores (dashpots).
oscarrosete.com
Solución LTI Differential equations
2 enfoques para la resolución de ecuaciones diferenciales
- Resolver en el dominio del tiempo.
- Resolver en el dominio s (frecuencia) utilizando la transformada de Laplace, la cual convierte ecuaciones diferenciales LTI a ecuaciones algebraicas.
oscarrosete.com
Solución LTI Differential equations
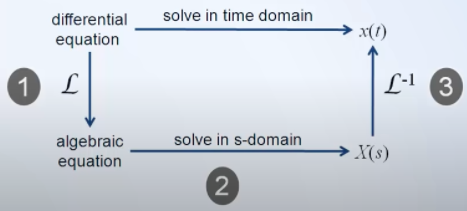
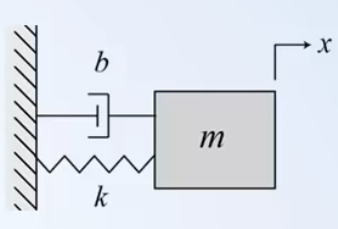
Consideremos el siguiente sistema mecánico del tipo dinámico compuesto por una masa, resorte y un amortiguador.
Obtengamos su modelo a partir de "primeros principios".
oscarrosete.com
Resolución dominio tiempo
oscarrosete.com
Obtención modelo
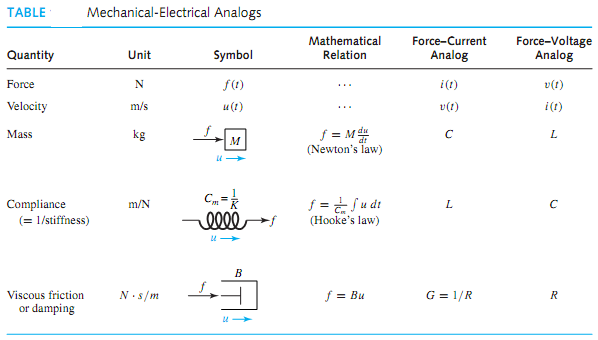
La mayoria de los sistemas de control contiene componentes tanto mecanicos como electricos, auuque algunos tambien tienen elementos neumaticos e hidraulicos. Desde punto de vista matematico los elementos mecanicos y electricos son analogos.
oscarrosete.com
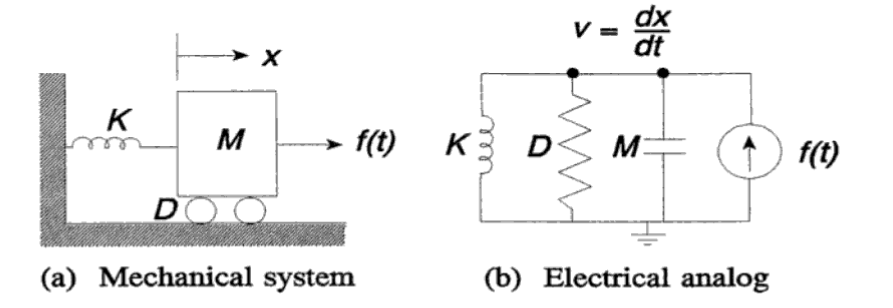
Ejemplo analogía
El siguiente sistema de masa resorte con un grado de libertad se puede visualizar como el circuito eléctrico mostrado en la figura derecha.
oscarrosete.com
Obtención modelo
El movimiento de traslación esta definido como un movimiento que toma lugar a lo largo de una línea recta. Las variables que se utilizan para describir el movimiento de traslación son la aceleración, velocidad y desplazamiento.
La ley del movimiento de Newotn establece que la suma algebraica de las fuerzas que actuan sobre un cuerpo rigido en una direccion es igual al producto de la masa del cuerpo por su aceleración en la misma dirección.

oscarrosete.com
Obtención modelo
En este tipo de sistemas, los siguientes elementos están involucrados:
- Masa (elemento inercial): propiedad de almacenar energía cinética del movimiento de traslaciónl. Análoga a la inductancia.
La ecuación de la fuerza se escribe como:

oscarrosete.com
Obtención modelo
En este tipo de sistemas, los siguientes elementos están involucrados:
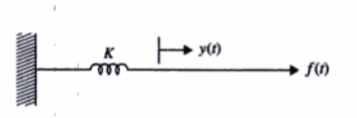
2. Resorte lineal: Un modelo de un resorte real o la compliancia de un cable o una banda. En general, un resorte esta considerado como un elemento que almacena energía potencial. Análogo a un capacitor.
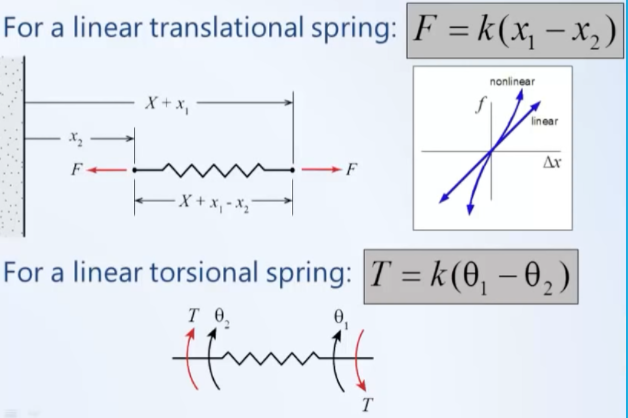
En la vida real son no lineales, pero si la deformación es pequeña se puede aproximar su coportamiento a la siguiente relación. K es la constante del resorte, o simplemente rigidez. Ley de Hooke
Si esta precargado con una tensión T
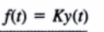
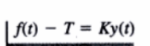
oscarrosete.com
Obtención modelo
Resorte lineal
oscarrosete.com
Obtención modelo
En este tipo de sistemas, los siguientes elementos están involucrados:
3. Fricción para el movimiento de traslacion
Cuando exista movimiento o tendencia de movimiento entre dos sistemas físicos, se presentarán fuerzas de friccion. Las fuerzas de friccion son de naturaleza no lineal y dependen de la composición de superficies, presion entre las mismas, velocidad relativa entre otras:
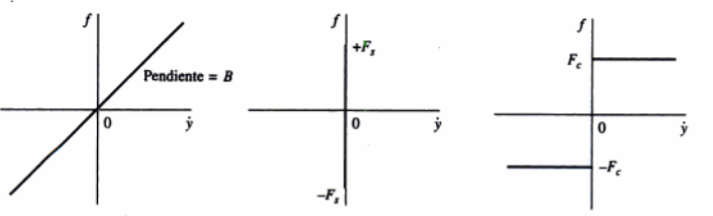
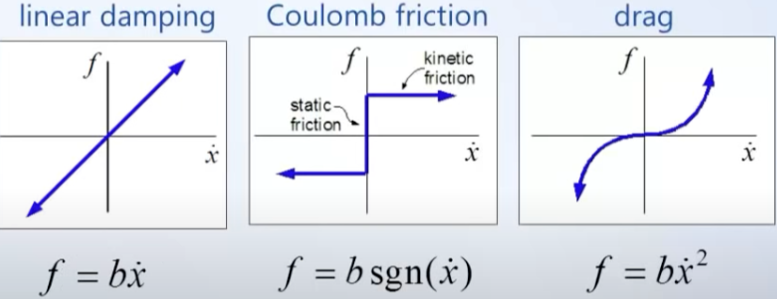
Existen tres tipos de fricción:
Fricción viscosa, estática y de coulomb
Figura inferior (izq a derecha)
oscarrosete.com
Obtención modelo
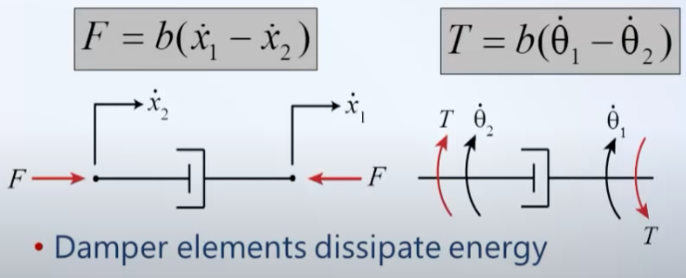
Fricción viscosa/amortiguador
oscarrosete.com
Obtención modelo
Fricción viscosa
3. Fricción para el movimiento de traslacion
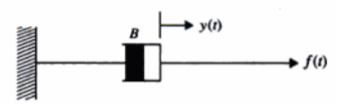
La fricción viscosa representa una fuerza que es una relación lineal entre la fuerza aplicada y la velocidad. A menudo, el esquema del elemento de fricción viscosa se representa como un amortiguador.
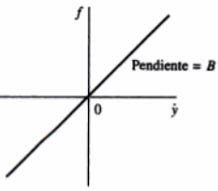
La expresión matemática de la fricción viscosa es:
donde b es el coeficiente de friccion viscosa
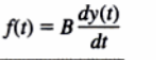
oscarrosete.com
Obtención modelo
Ecuaciones de sistemas mecánicos
Las ecuaciones de un sistema mecánico lineal se escriben, primero construyendo un modelo del sistema que contenga los elementos lineales conectados y luego se aplica la ley del movimiento de Newton al diagrama de cuerpo libre.
Para el movimiento de traslación se emplea:
oscarrosete.com
Pasos obtención modelo
- Seleccionar coordenadas y orientación
- Dibujar diagrama de cuerpo libre para cada elemento inercial.
- Generar ecuaciones de movimiento utilizando la segunda ley de Newton y la segunda ley de Euler.
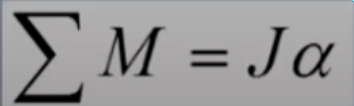
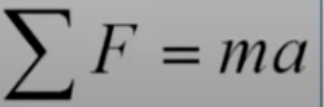
oscarrosete.com
Obtención modelo
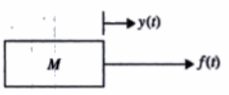
Considere el sistema de masa-resorte-fricción (amortiguador) que se muestra en la figura. El movimiento lineal de interés es el de dirección horizontal (traslación)

oscarrosete.com
Obtención modelo
Realizando un diagrama de cuerpo libre donde se aplica una fuerza f(t) las fuerzas involucradas se verían como se muestra en el siguiente diagrama de cuerpo libre:
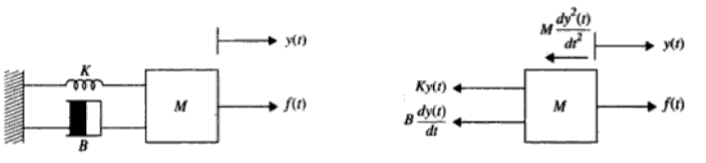
oscarrosete.com
Representación en notación de newton

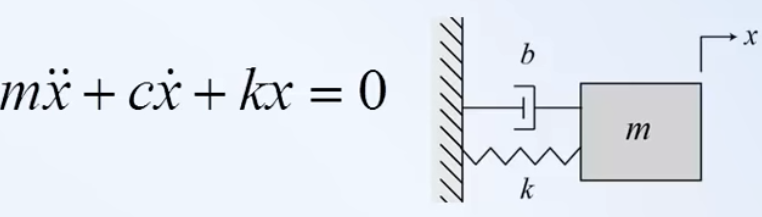
oscarrosete.com
Ecuaciones diferenciales
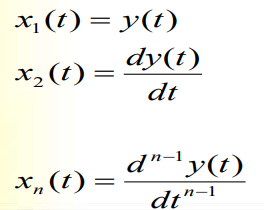
La ecuacion diferencial de un sistema de n-ésimo orden se escribe como:
Se le llama ecuacion diferencial ordinaria lineal.
Se puede descomponer en n ecuaciones diferenciales de primer orden.
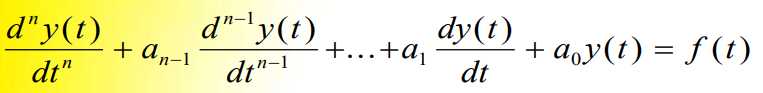
oscarrosete.com
Respuesta del sistema


oscarrosete.com
Respuesta natural
Si las raices son completamente reales, la solución es del tipo exponencial
- Si son negativas el sistema es estable
- si son positivas el sistema es inestable
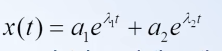

oscarrosete.com
Respuesta natural
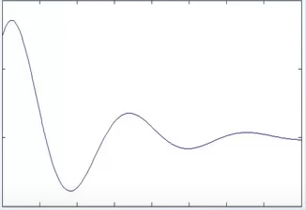
Si las raices son complejas, se puede reescribir en terminos de senos y cosenos utilizando la identidad de euler.
parte real=tasa de decaimiento
parte imaginaria= frecuencia de oscilación.
si exponencial =0?
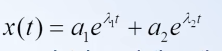

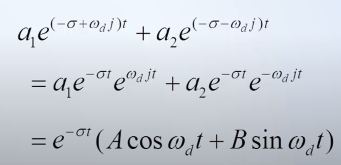

oscarrosete.com
Respuesta del sistema
oscarrosete.com
Respuesta elementos mecánicos
oscarrosete.com
Ejercicio real alumnos

Considere el sistema de masa-resorte-fricción (amortiguador) que se muestra en la figura. El movimiento lineal de interés es el de dirección horizontal (traslación)
B=4Ns/m m=2kg k=2N/m xo=1m vo=0m/s
B=coeficiente de amortiguamiento viscoso

2 enfoques para la resolución de ecuaciones diferenciales
- Resolver en el dominio del tiempo.
- Resolver en el dominio s (frecuencia) utilizando la transformada de Laplace, la cual convierte ecuaciones diferenciales LTI a ecuaciones algebraicas.
oscarrosete.com
Solución LTI Differential equations

oscarrosete.com
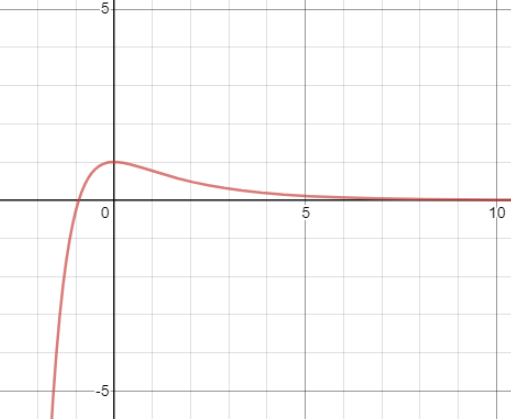
Ejercicio real alumnos
Considere el sistema de masa-resorte-fricción (amortiguador) que se muestra en la figura. El movimiento lineal de interés es el de dirección horizontal (traslación)
B=5Ns/m m=2kg k=2N/m xo=1m vo=0m/s
B=coeficiente de amortiguamiento viscoso

oscarrosete.com
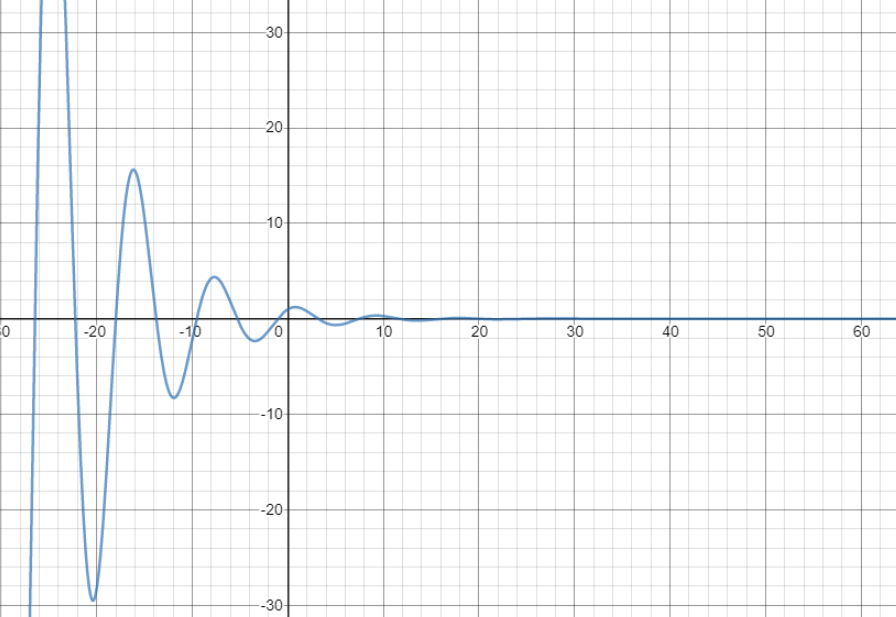
Ejercicio real alumnos
Considere el sistema de masa-resorte-fricción (amortiguador) que se muestra en la figura. El movimiento lineal de interés es el de dirección horizontal (traslación)
B=0.3Ns/m
m=1kg
k=9/4 N/m
xo=1m vo=0m/s

oscarrosete.com
Ejercicio real alumnos
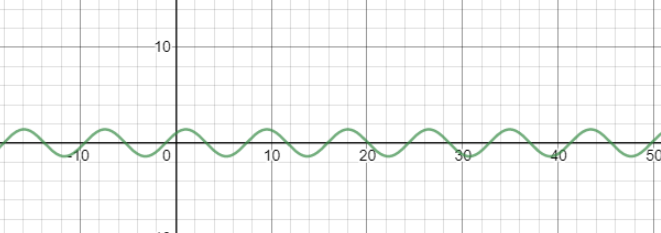
Considere el sistema de masa-resorte-fricción (amortiguador) que se muestra en la figura. El movimiento lineal de interés es el de dirección horizontal (traslación)
B=0Ns/m
m=1kg
k=9/4 N/m
xo=1m vo=0m/s

oscarrosete.com
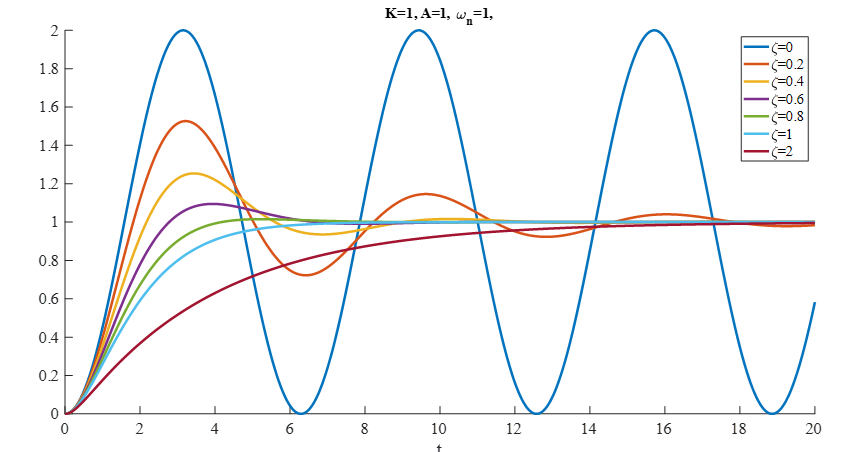
Comportamiento posible respuesta transitoria de un sistema de segundo orden
2 enfoques para la resolución de ecuaciones diferenciales
- Resolver en el dominio del tiempo.
- Resolver en el dominio s (frecuencia) utilizando la transformada de Laplace, la cual convierte ecuaciones diferenciales LTI a ecuaciones algebraicas.
oscarrosete.com
Transformada de Laplace

Es una operacion matematica que toma una ecuación en el dominio del tiempo y la convierte al dominio s (frecuencia)
Tiene las siguientes ventajas:
– La solución de la ecuación homogénea y la solución particular en una sola operación.
– Convierte la ecuación diferencial en una ecuación algebraica en S
oscarrosete.com
Transformada de Laplace
Es una operacion matematica que toma una ecuación en el dominio del tiempo y la convierte al dominio s (frecuencia)
Utilidad: Convertir ecuaciones diferenciales a algebraicas
oscarrosete.com
Transformada de Laplace
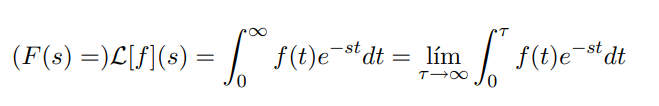
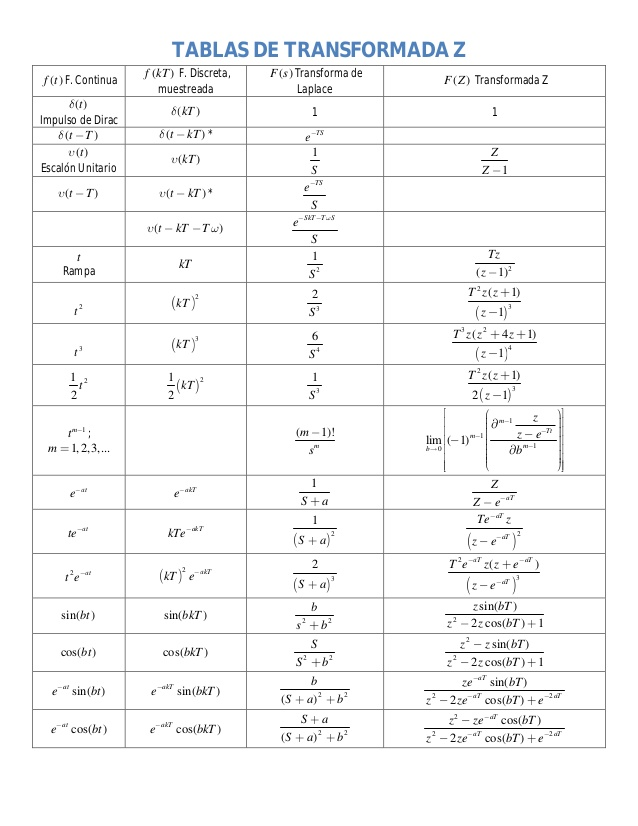
Generalmente nos ayudamos en tablas de referencia para obtener la transformada de laplace.
Sugerencia:
https://es.khanacademy.org/math/differential-equations/laplace-transform
Tabla:
oscarrosete.com
Transformada de Laplace
Las propiedades clave que nos ayudan para manipularlas al resolver ecuaciones diferenciales.
Son la linealidad, desplazamiento de frecuencia y de diferenciación enésima
oscarrosete.com
Transformada de Laplace
oscarrosete.com
Transformada inversa de Laplace
Consiste en pasar del dominio s al dominio del tiempo. Generalmente nos ayudamos en tablas de referencia para obtener la transformada inversa de laplace.

oscarrosete.com
Proceso completo

Para resolver una ecuación diferencial lineal ordinaria el procedimiento es :
– Transformar la ecuación diferencial al dominio s.
– Manipular la ecuación algebraica y resolver para la variable de salida.
– Expandir en fracciones parciales.
– Obtener transformada inversa de Laplace
oscarrosete.com
Proceso completo
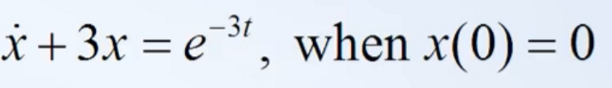

oscarrosete.com
Ejercicio alumnos
Encontrar la respuesta del sistema representado por la siguiente ecuación diferencial con el apoyo de transformada de Laplace.
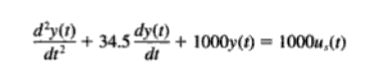
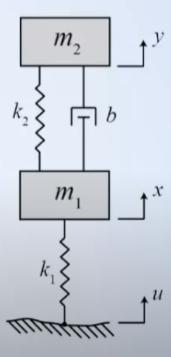
Encontrar el modelo del siguiente sistema conformado por amortiguador, 2 masas 2 resortes.
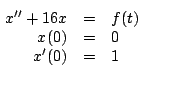
0