Fluctuations in               biofilm topographies

Pablo Bravo

YunkerLab, Georgia Institute of Technology

APS March Meeting 2023

smooth

Extracellular matrix formed of polysaccharides, DNA, and proteins 

Surface

Interface

Cells

Biofilms are                                                    3D structures

complex surface-attached

Surface

Interface

Cells

Can we learn about the biofilm development/composition by looking at its topography?

Biofilms are                                                    3D structures

complex surface-attached

What is                                    ?

Profiles are flat. A few cells in amplitude, over thousands of micrometers!

\(500 \mu m\)

biofilm topography

Using white-light interferometry, we can capture the profiles of a growing colonies for extended periods of time

                                           are different between strains

Staphylococcus aureus

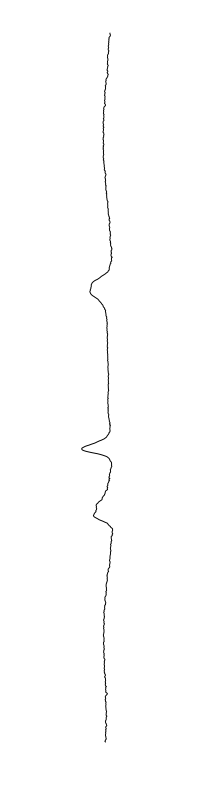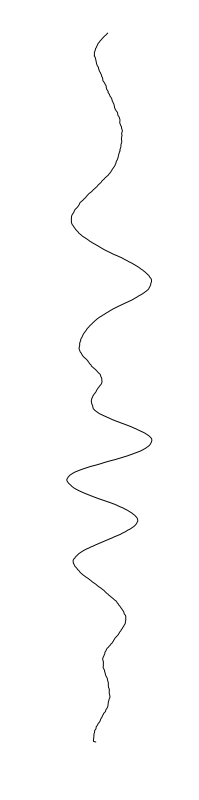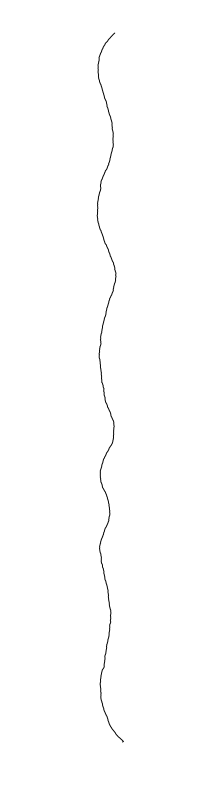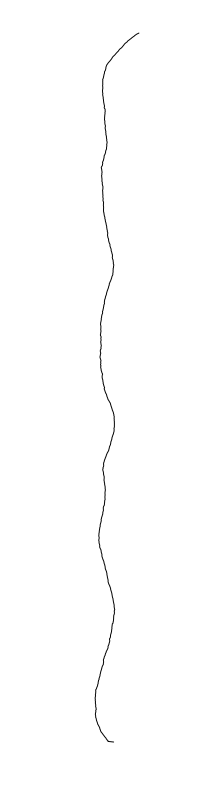
Bacillus cereus

Eschericia coli

  • What is leading to the differences between profiles?
  • How do we characterize the dynamics?

\(2 mm\)

\(8 \mu m\)

Time since inoculation [hours]

\(0\)

\(24\)

\(48\)

Fluctuation dynamics

Fluctuations can 

Aeromonas veronii

Eschericia coli

or

relax

increase

  • Width of perpendicular fluctuations in the height profile:

 

 

  • With a roughness/Hurst scaling exponent \(H\):

     
  • The width saturates at \(l_\text{sat}\), and across the whole sample the width is \(w_\text{sat}\)
w_l(\mathbf{r}, t) = \langle (h (\mathbf{r}, t) - \langle h(\mathbf{r}, t) \rangle_l )^2 \rangle_l^{1/2}

\(w_l(t) \propto l^{H} \)

                        fluctuations

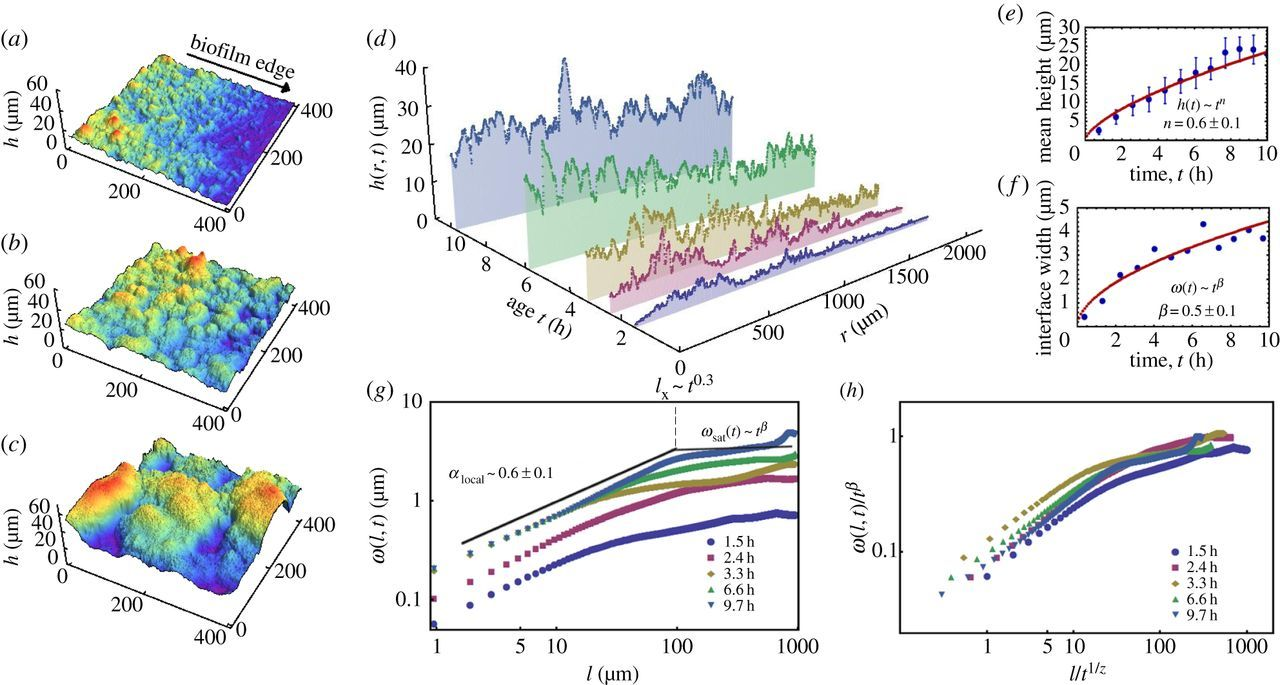
Dervaux, et al. 2014

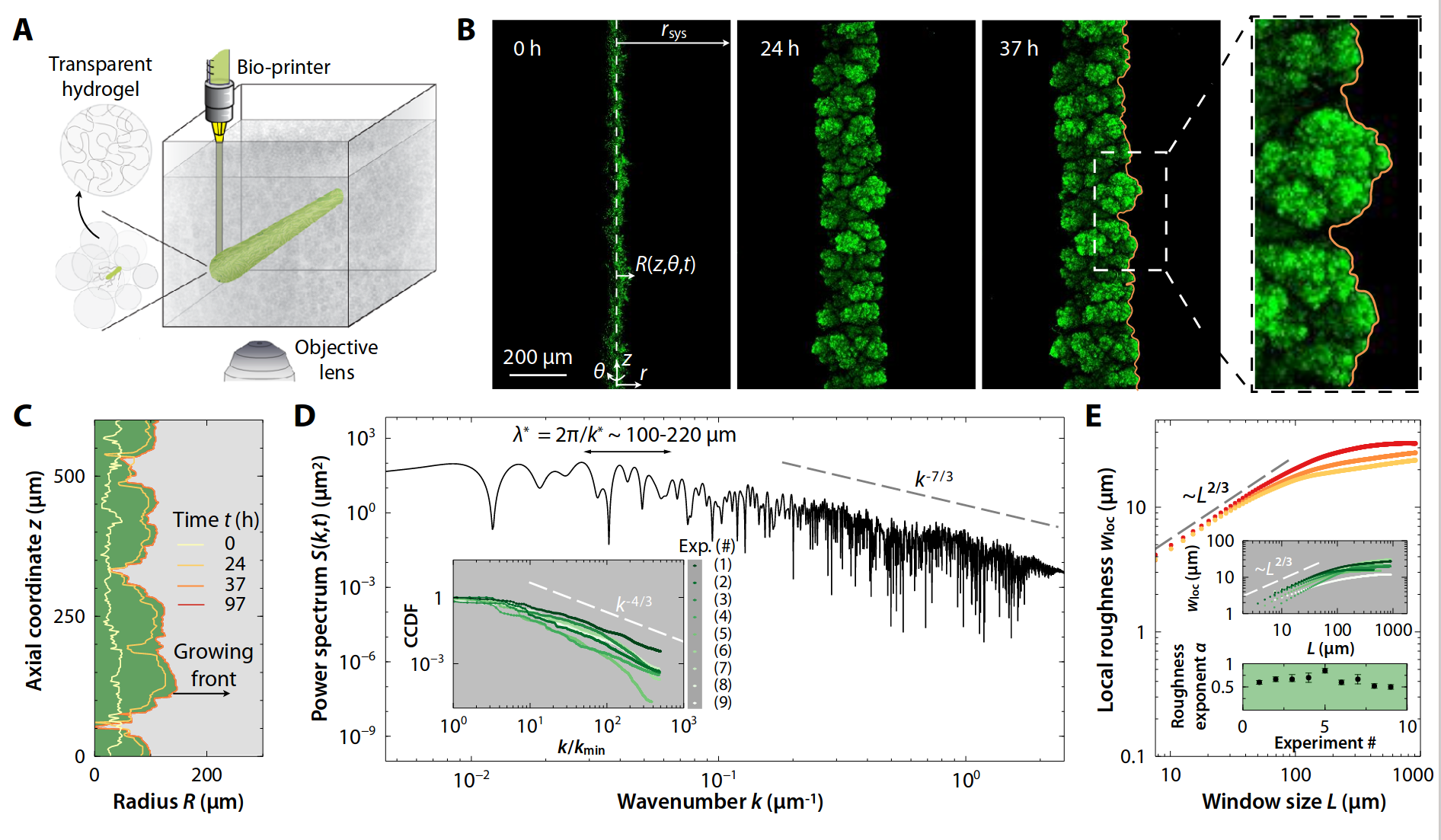
Martinez-Calvo and Bhattacharjee, et al. 2022

\(H\)

\(l_{\text{sat}}\)

\(w_{\text{sat}}\)

Quantifying

                        across strains

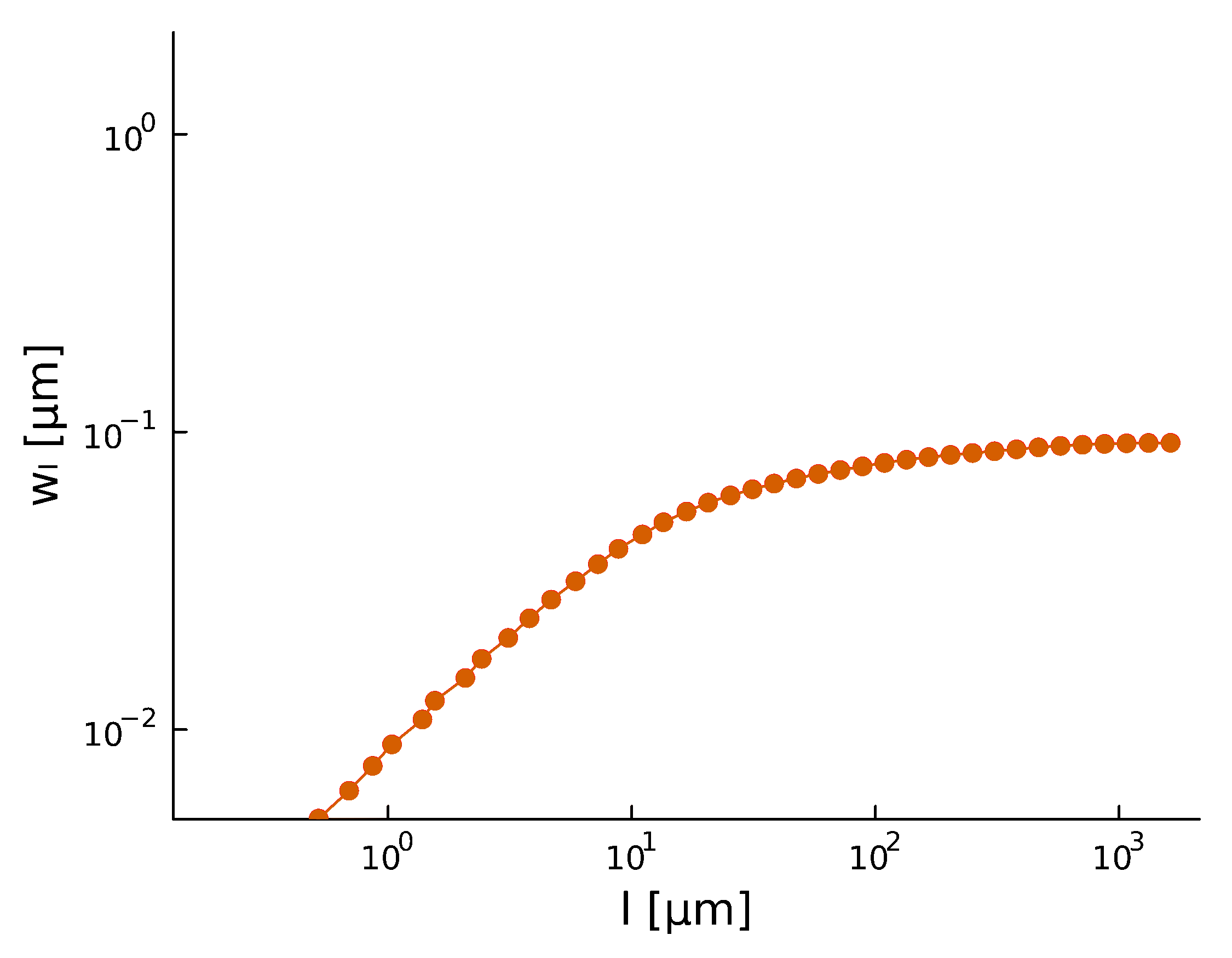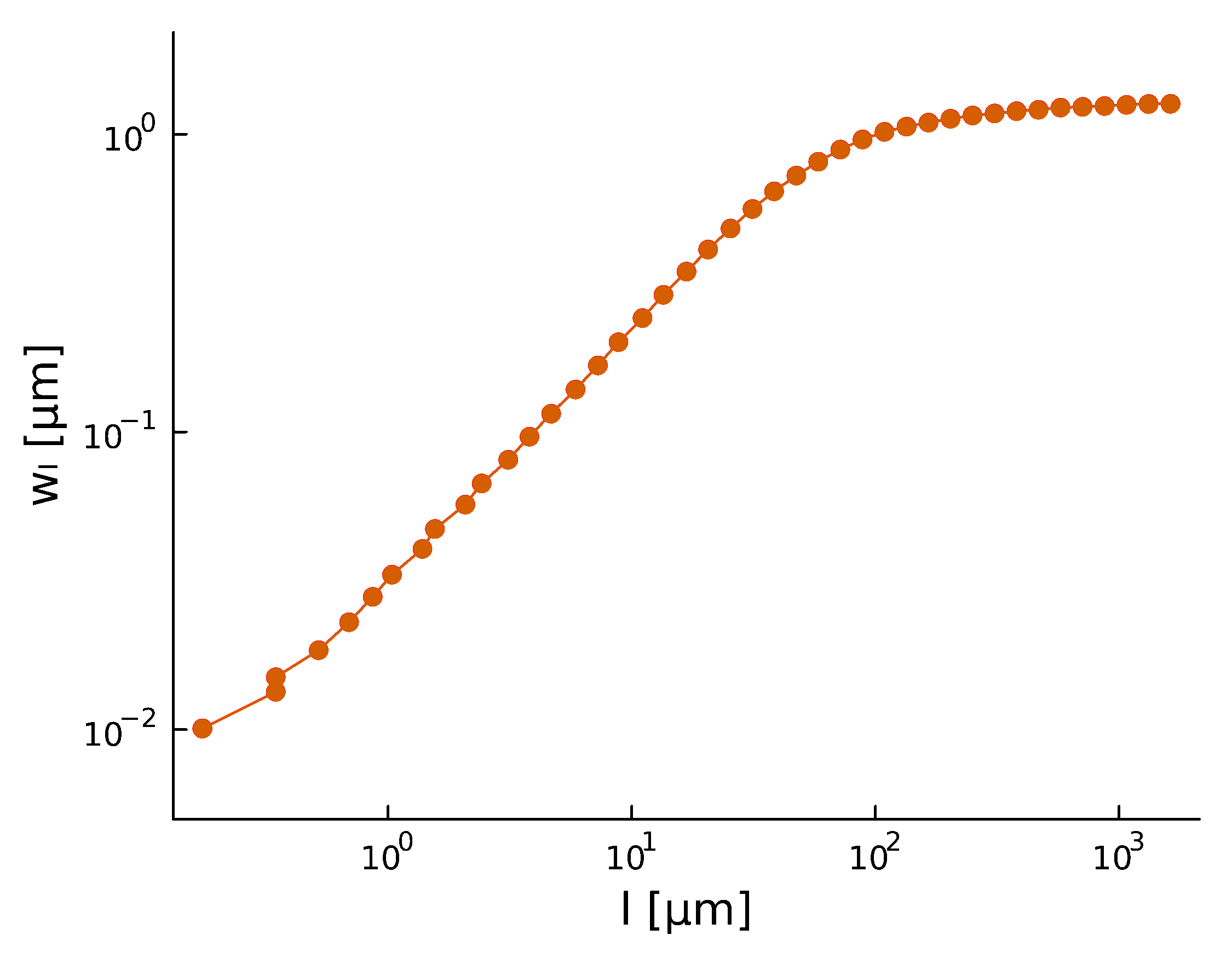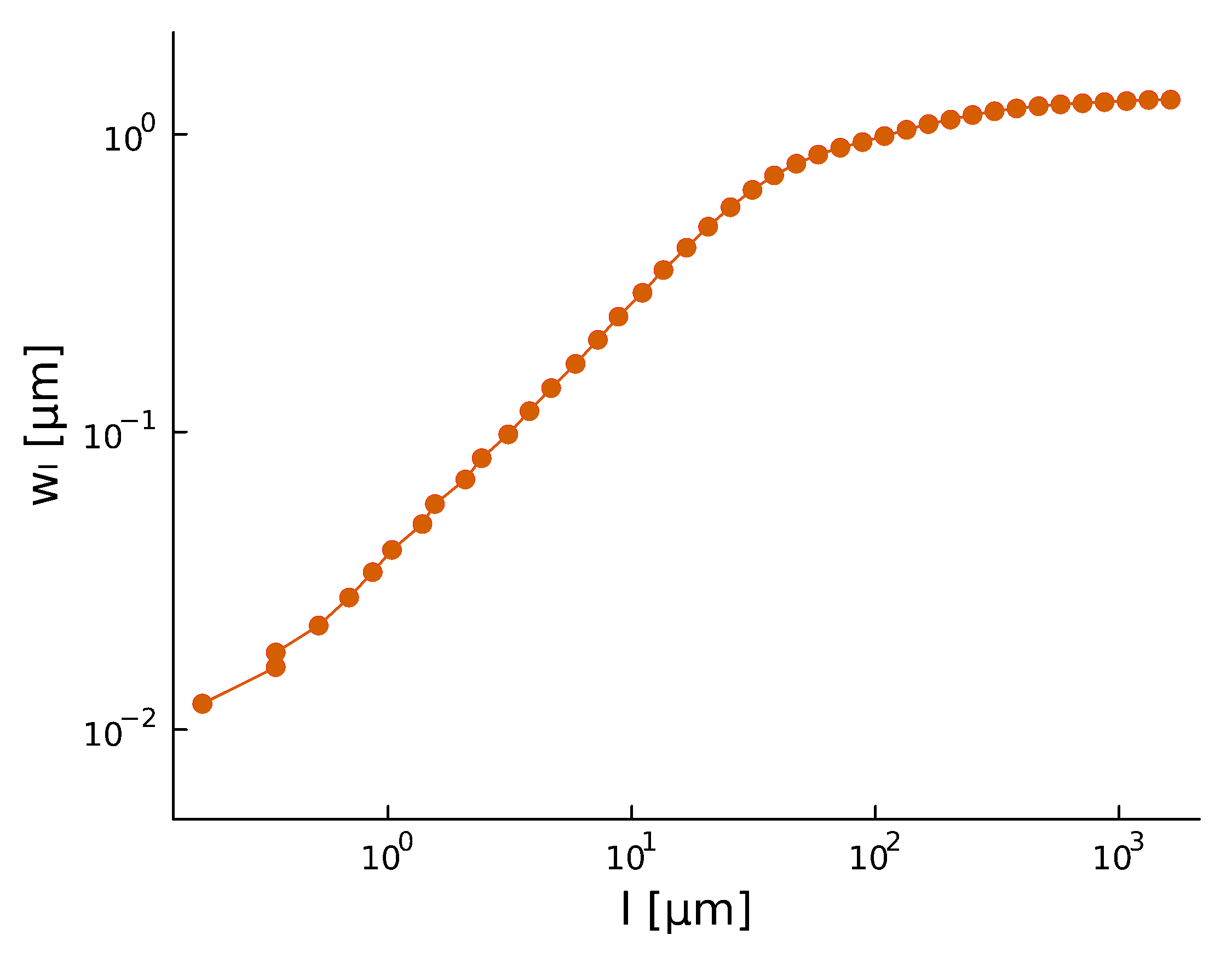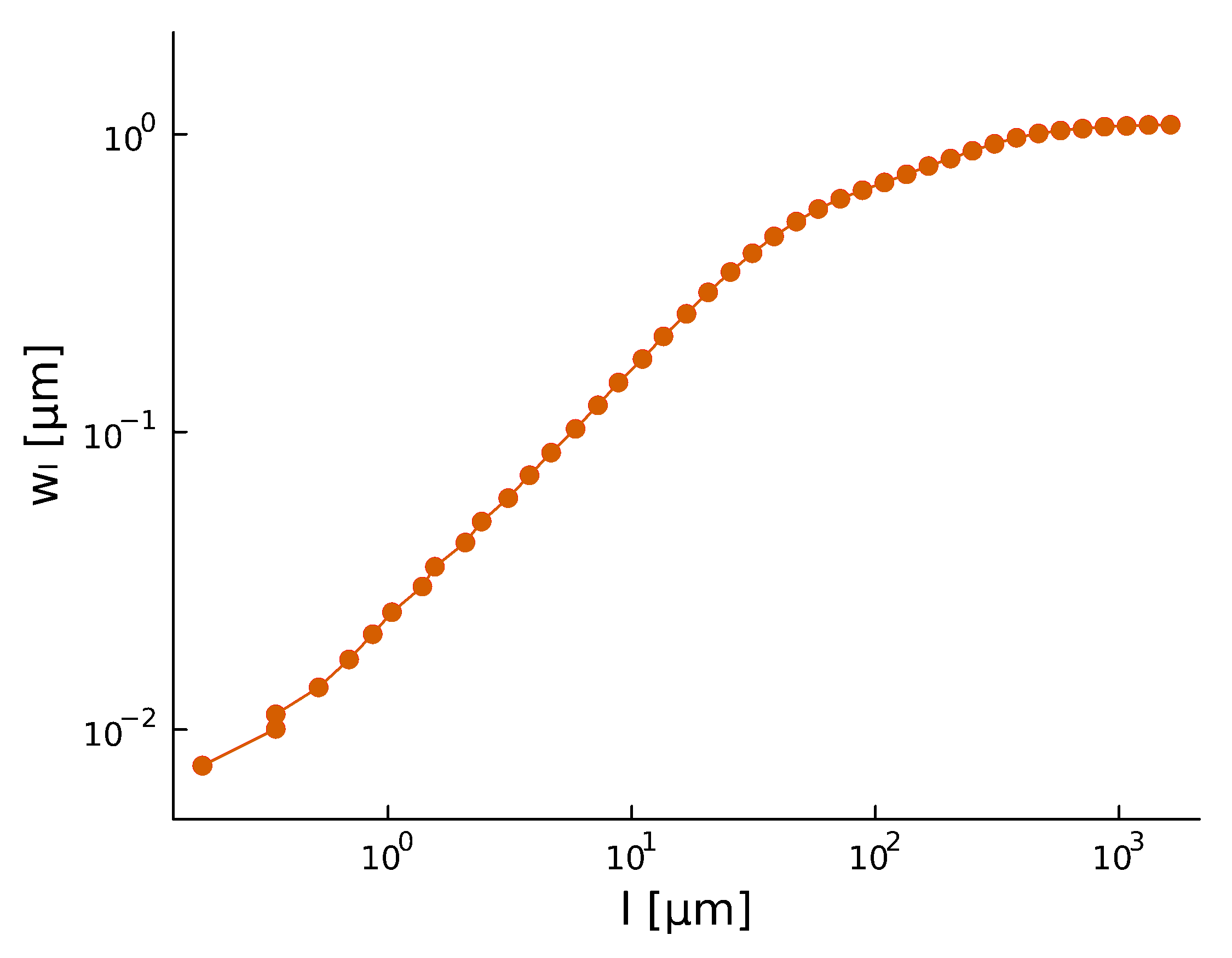
Roughness \(H\), after a period of time, stabilizes at \(H_{\text{steady}} \sim 0.8\)

Roughening

         and

There is high variability between microbes

\(w_{sat}\)

vertical growth

                         during biofilm growth

\frac{\partial h}{\partial t} = \alpha \cdot \text{min}(h, L) - \beta \cdot h\\

Growth rate

Decay rate

Diffusion length

Two regimes

doi.org/10.1101/2022.08.11.503641

In press at PNAS

There is high variability between microbes

And an apparent correlation between vertical growth dynamics and the topography!

Colonies reach nutrient depletion length \(L\)

Knowing the moment when the colony is growing the fastest, just by looking at                         

fluctuations

         and

\(w_{sat}\)

vertical growth

Are fluctuations                   ?

\(S(k) [\mu m^4]\)

\(k [\mu m^{-1}]\)

\(10^4\)

\(10^3\)

\(10^2\)

\(10^1\)

Dynamic scaling, a test for self-affinity requires: 

 

\(\nu = 1+2H\)

We do not see observe dynamic scaling. 

It is close but not the same!

scale-free

Testing                       again

self-affinity

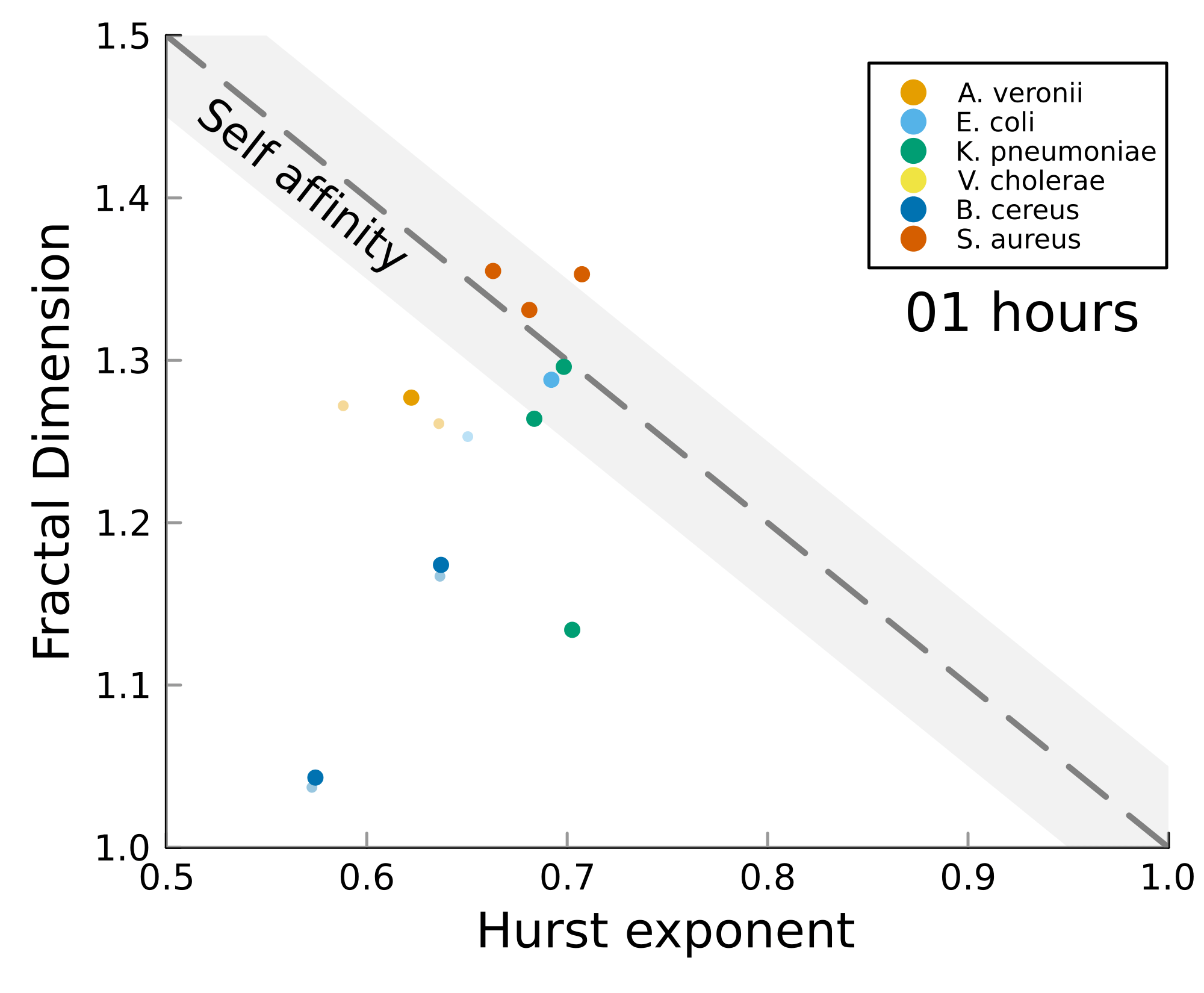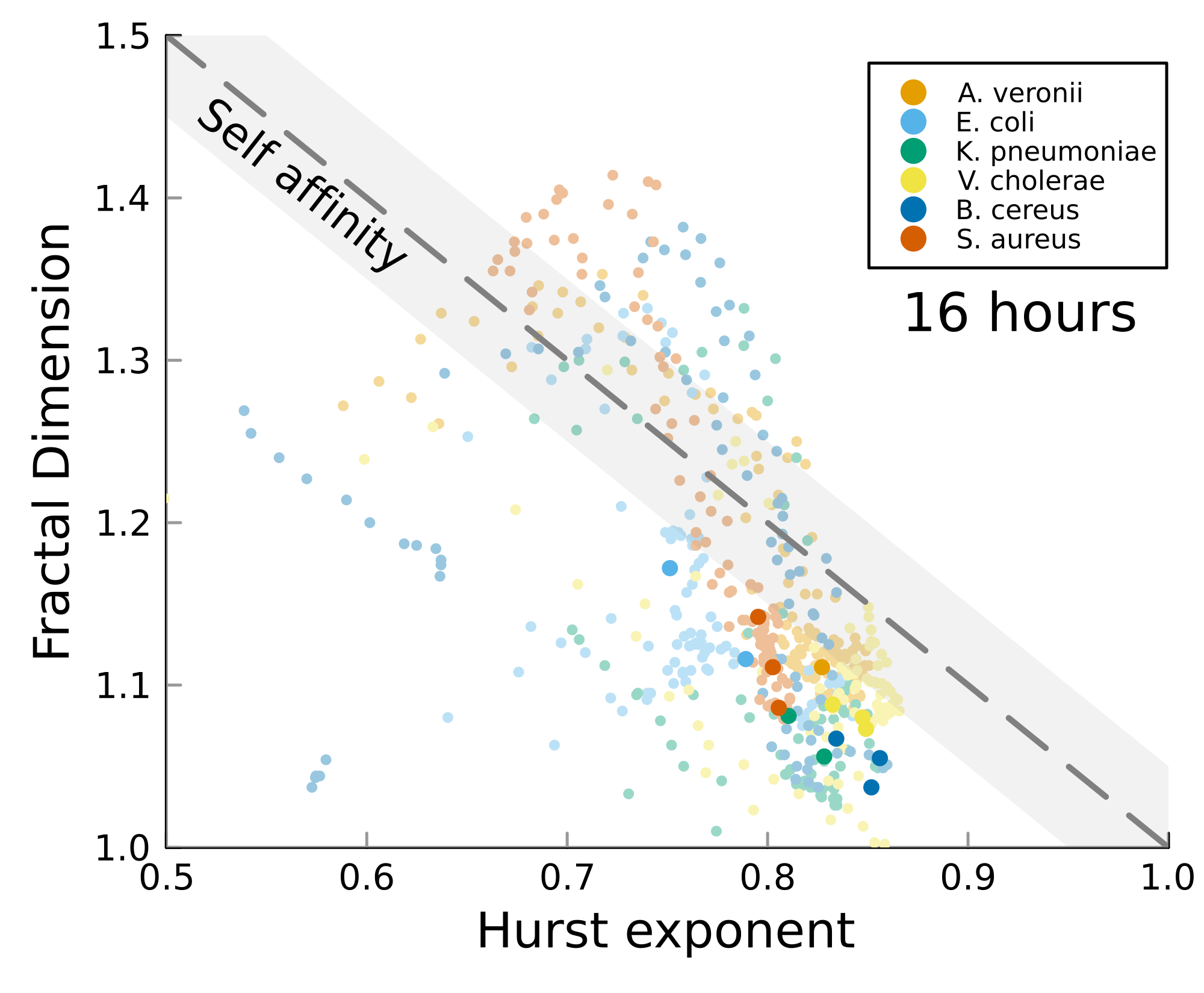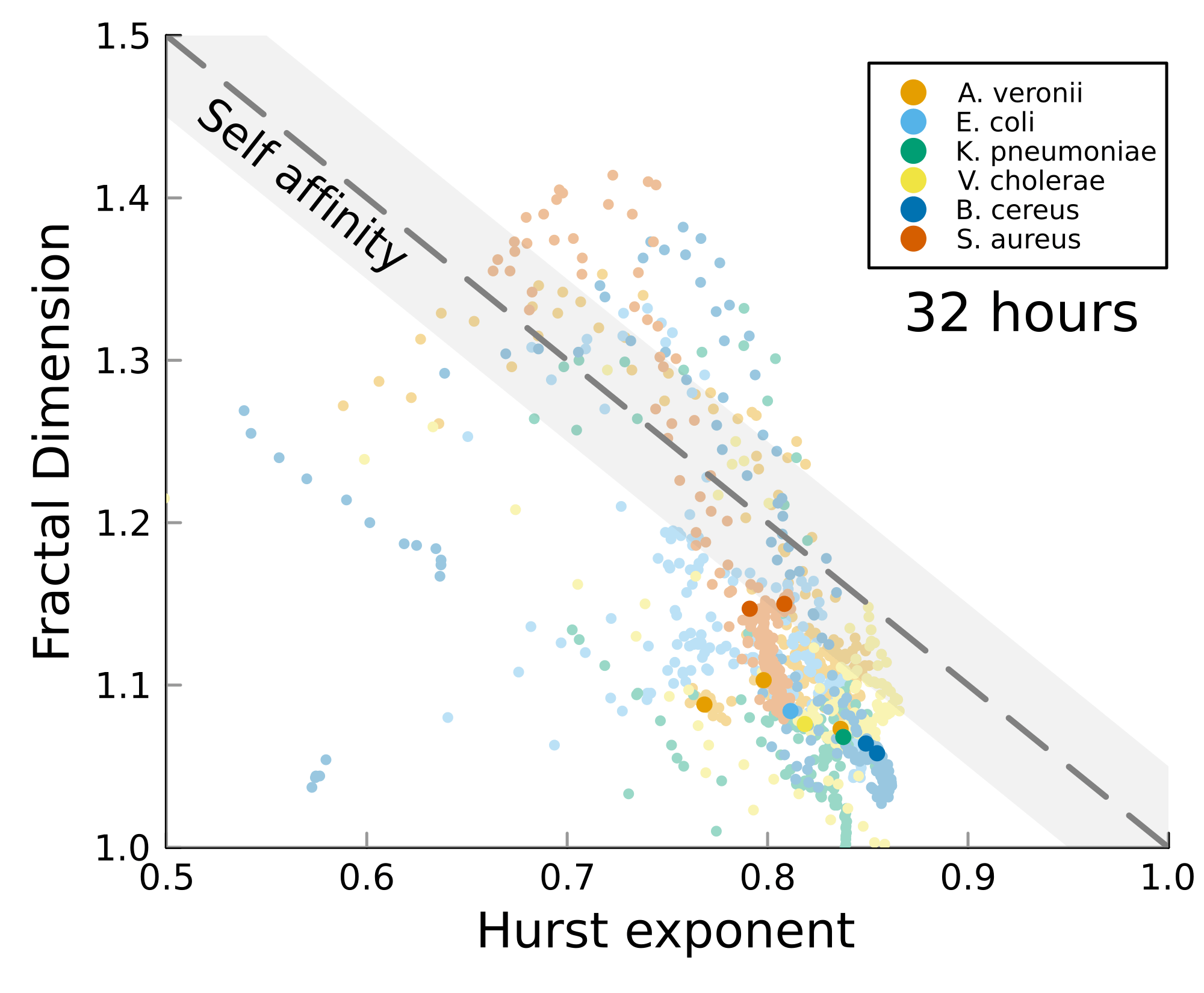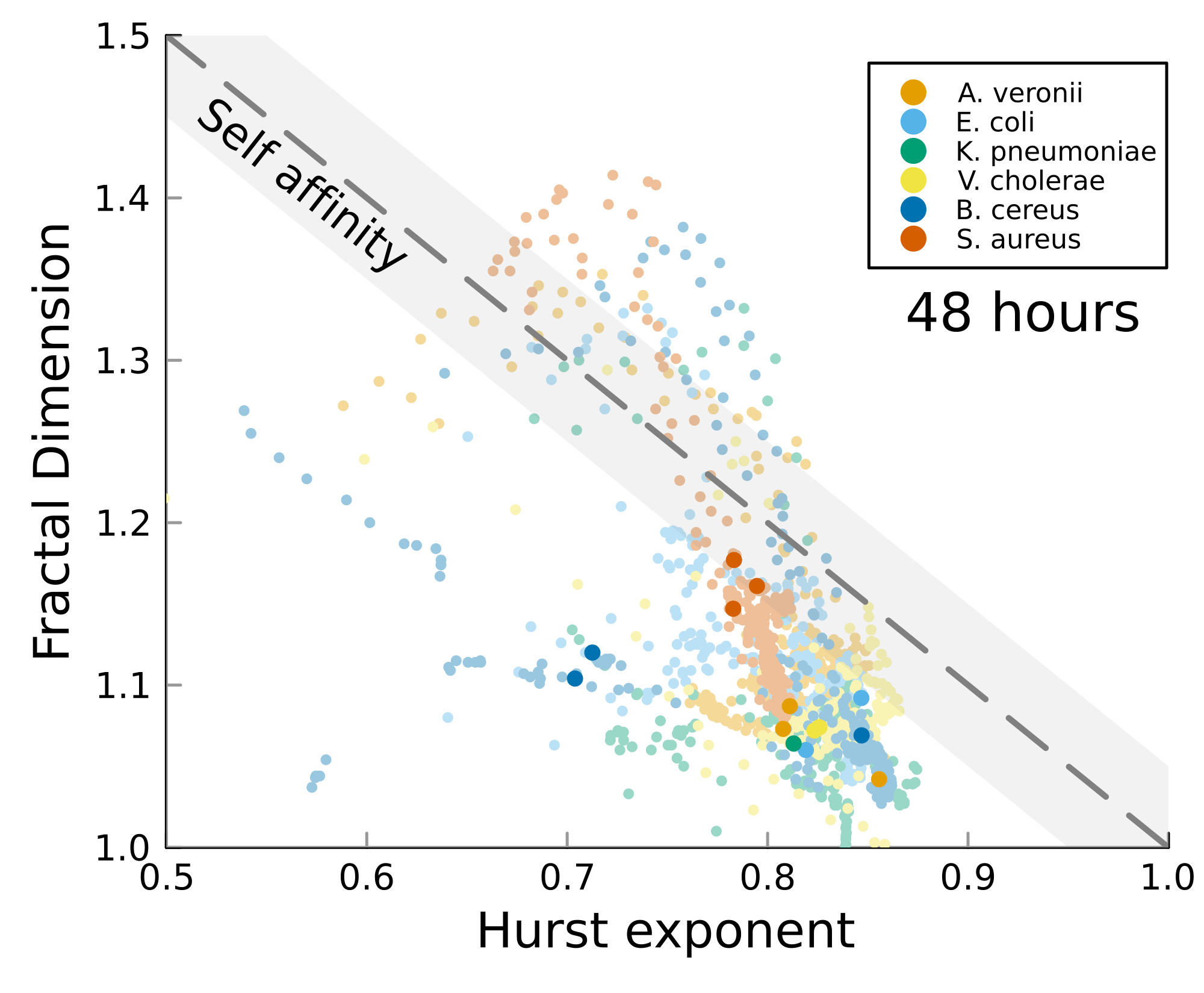
We can test self-affinity using the fractal dimension \(D\)

\(D + H = 2\)

\(D + H = n +1\), where \(n\) is the base dimension of the system

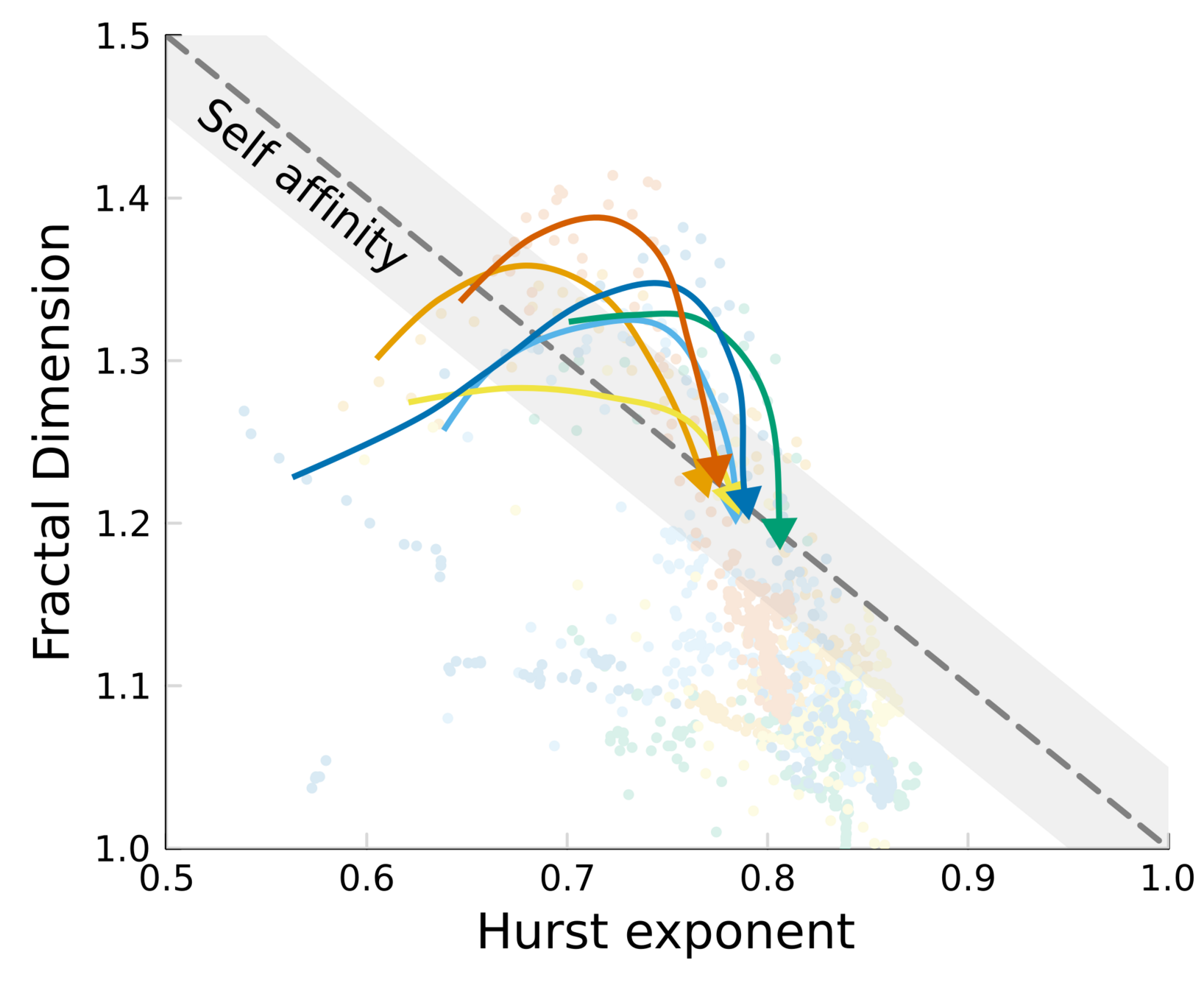
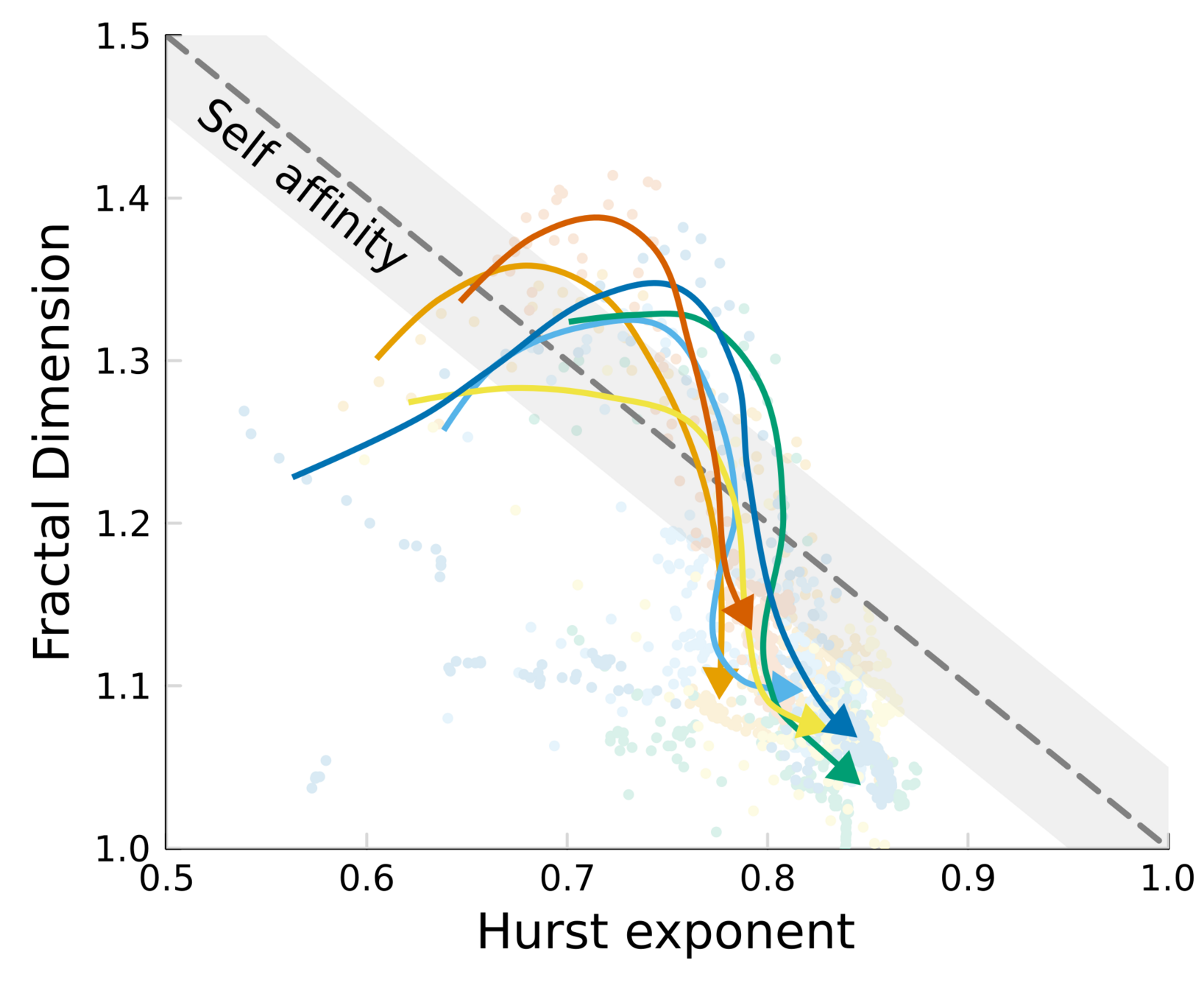
Topography dynamics as a consequence of growth through a viscoelastic material:

  1. Reach SA while growth is fast
  2. Relax when the colony is tall, and fluctuations get damped

Acknowledgements

NIH-NIMS

NSF BMAT

Biolocity

Dr. Peter Yunker

Dr. Brian Hammer

Dr. Siu Ling Ng

Dr. Thomas Day

Aawaz Pokhrel

Emma Bingham

Funding

Thanks!

Adam Krueger

Raymond Copeland

Maryam Hejri

Lin Zhao

Chris Zhang

 

Can we establish a link between                          and                                          ?

Hopefully!

topographies

biofilm development