Contact Estimation from External Joint Torque Measurements on a serial robotic arm

\newcommand{\rv}[1]{\mathsfit{#1}} \newcommand{\rvv}[1]{\bm{\mathsfit{#1}}}

Tao Pang, Jack Umenberger and Russ Tedrake

Robot Locomotion Group

{pangtao, ju, russt}@csail.mit.edu

Motivation

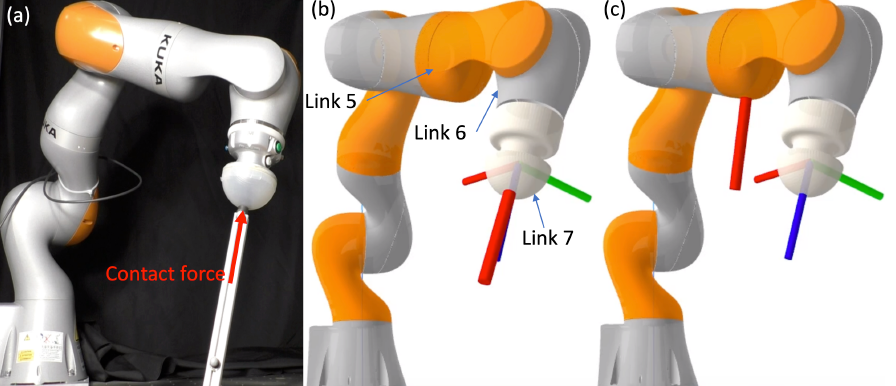
estimated contact force

  • Robot arms such as KUKA IIWA and FRANKA PANDA can estimate \(\tau_{\text{ext}}\) using the generalized momentum observer.
  • Assuming there is one external, point-contact force, existing methods can estimate \(\bm{p}_C\) and \(\bm{f}_C\) from \(\tau_{\text{ext}}\).
  • However, some \(\tau_{\text{ext}}\) can be explained equally well by multiple contact points.

Haddadin, Sami, Alessandro De Luca, and Alin Albu-Schäffer. "Robot collisions: A survey on detection, isolation, and identification." IEEE Transactions on Robotics 33.6 (2017): 1292-1312.

Manuelli, L. and Tedrake, R., 2016, October. Localizing external contact using proprioceptive sensors: The contact particle filter. In 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 5062-5069).

  • Existing methods do not take into account multiple solutions.
    • The method by Haddadin et al. returns a contact point on the last link with non-zero torque measurement.
    • Contact Particle Filter by Manuelli and Tedrake can return either one of the solutions. 
  • Goal: estimating from only external torque \(\tau_{\text{ext}}\)
    •  \(\bm{p}_C \in \mathcal{S}\): contact point C on the robot's surface \(\mathcal{S}\).
    • \(\bm{f}_C \in \mathbb{R}^3\): contact force at point C.
M(q)\ddot{q} + C(q, \dot{q}) + \tau_g = \tau_{\text{m}} + \tau_{\text{ext}}

motor torque.

external torque due to contact

gravitational torque.

joint angles.

Coriolis.

Mathematically...

  • We would like to solve

for the contact position \(\bm{p}_C\) and contact force \(\bm{f}_C\), subject to 

  •  \(\bm{p}_C \in \mathcal{S}\): point C is on the robot's surface.
  • \(\bm{f}_C \in \mathcal{K}_C\): force \(\bm{f}_C\) is inside the friction cone at C.
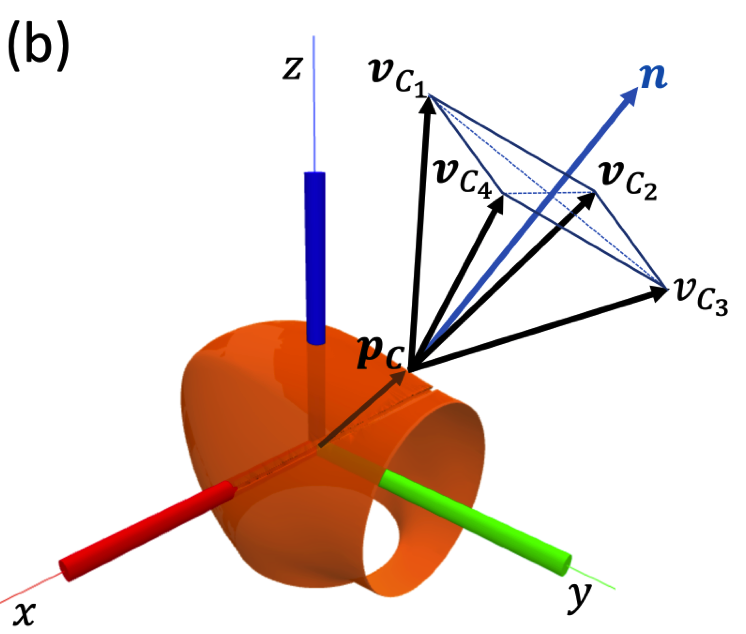
\bm{\tau}_\text{ext} = \bm{J}_C(\bm{q}, \bm{p}_C)^\intercal \bm{f}_C,
  • This is equivalent to solving
\underset{\bm{\beta} \geq 0, \; \bar{\bm{p}}_C \in \mathcal{S}}{\text{min.}} \; \| \bm{J}(\bm{q}, \bar{\bm{p}}_C)^{\intercal} \bm{\beta} - \bm{\tau}_\text{ext} \|^2.
  • The minimum squared error of at a known point C can be obtained by solving a quadratic program (QP):
  • Common assumptions:
    • Only one external contact.
    • Contacts create no moment about the contact point.

Components of \(\bm{f}_C\) along \(\bm{v}_{C_i}\).

Link 6 of IIWA.

  • Finding all possible contact positions is the same as finding all global minima of
l(\cdot; \bm{q}, \bm{\tau}_\text{ext})
\newcommand{\tauE}{\bm{\tau}_{\text{ext}}} \newcommand{\pCbar}{\bar{\bm{p}}_C} l(\pCbar; \bm{q}, \tauE) \coloneqq \underset{\bm{\beta} \geq 0}{\text{min.}} \; \| \bm{J}(\bm{q}, \pCbar)^{\intercal} \bm{\beta} - \bm{\tau}_\text{ext} \|^2

The landscape of 

               on the robot's surface \(\mathcal{S}\)

l(\cdot; \bm{q}, \bm{\tau}_\text{ext})
  • We propose an algorithm to find all local minima of
  • Considering that torque measurements are noisy, knowing the local minima in addition to the global ones could actually be beneficial.  
l(\cdot; \bm{q}, \bm{\tau}_\text{ext})

Find all local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling

  • Sample points on the robot's surface, take the points with \(l \leq \epsilon\).
  • Rejection rate is 98% with \(\epsilon = 0.005\).

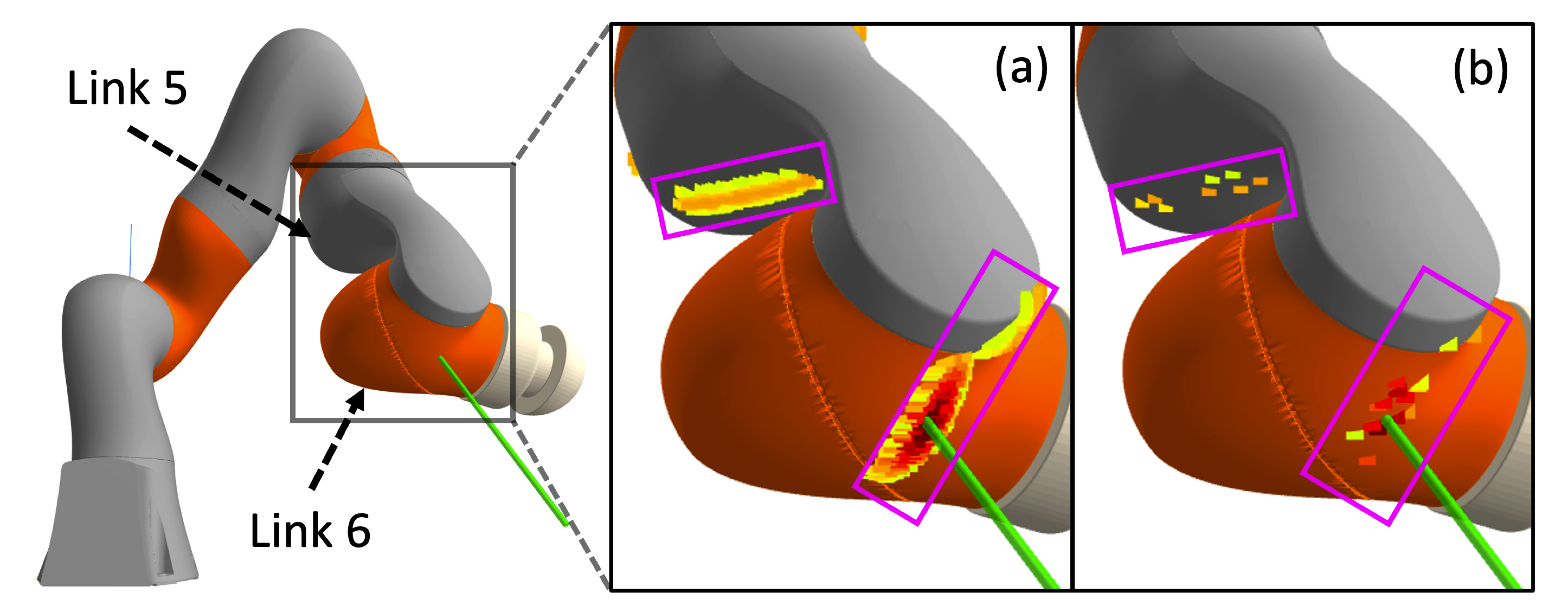
(a): accepted samples out of 10000 samples/link.

(b): accepted samples out of 500 samples/link.

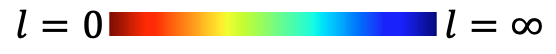
Find all local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent (RSGD)

  1. Rejection sampling with a larger threshold \(\delta\). 
    1. For example, acceptance rate rises to 17.5% with \(\delta = 0.1\)
  2. Run gradient descent on the accepted samples to converge to local minima of \(l(\cdot)\).
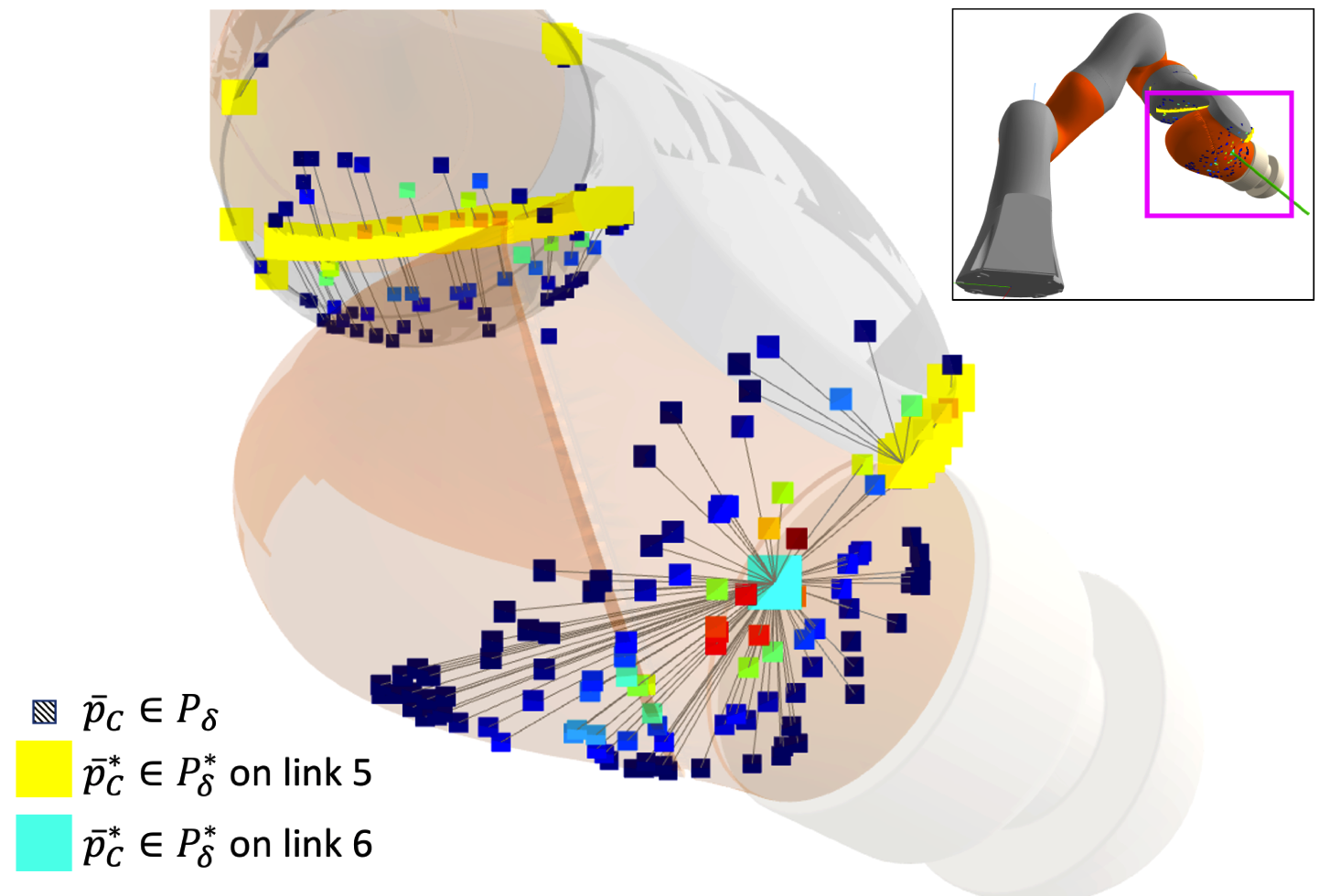
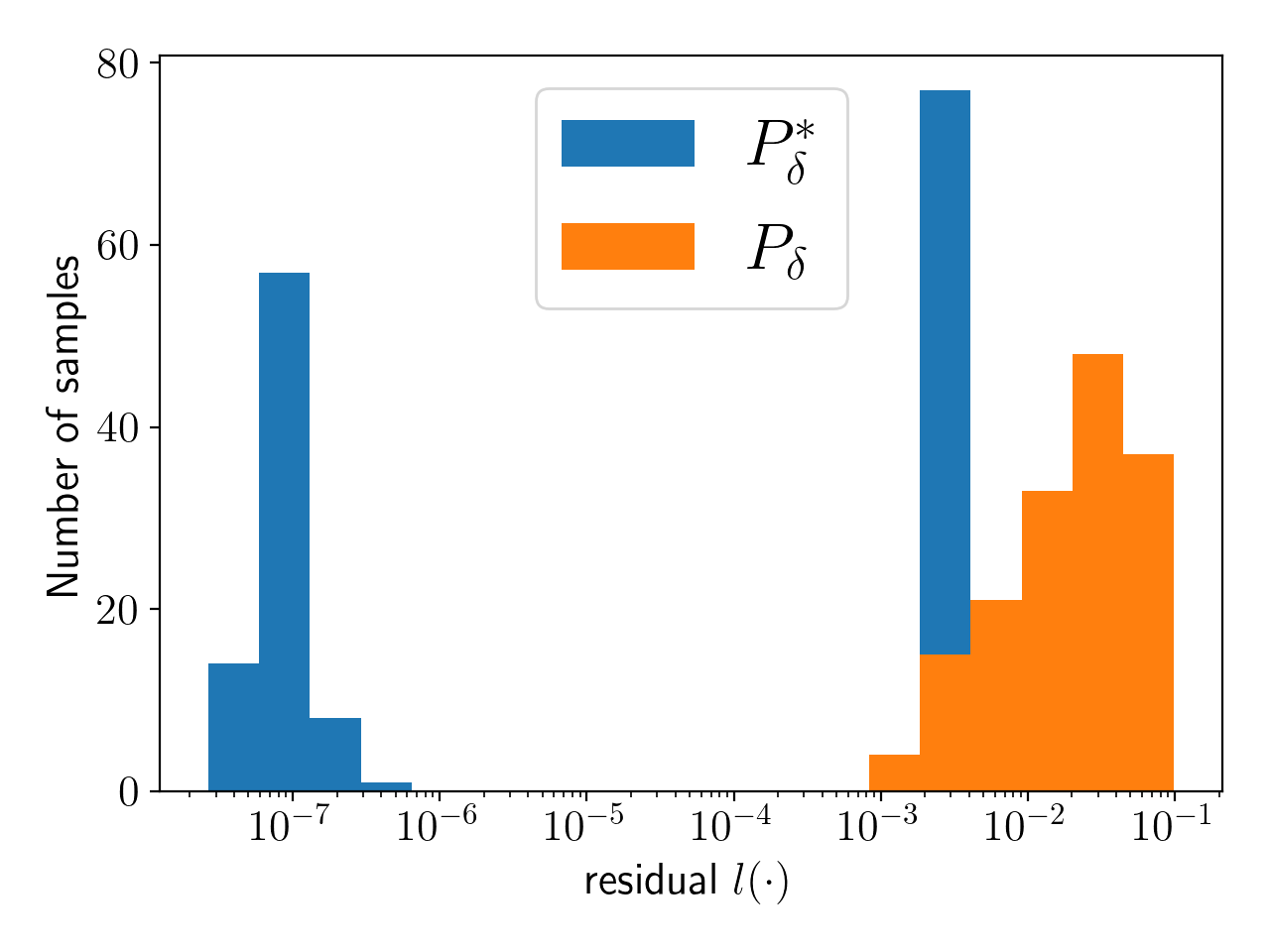
  • \(P_\delta\): set of accepted samples.
  • \(P_\delta^*\): set of optimized samples.

Find all local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent (RSGD)

  • \(P_\delta\): set of accepted samples.
  • \(P_\delta^*\): set of optimized samples.
  • Accepted / all samples: 172/1000
  • Link  5 ,  converged_samples / accepted samples: 78/84
  • Link  6 ,  converged_samples / accepted samples: 80/88

Works in other cases too! Runs at 10Hz on average.

Active Contact Discrimination

  • Disambiguate candidate contact positions found by Rejection Sampling + Gradient Descent by making small motions.

Active Contact Discrimination

  • Disambiguate candidate contact positions found by Rejection Sampling + Gradient Descent.

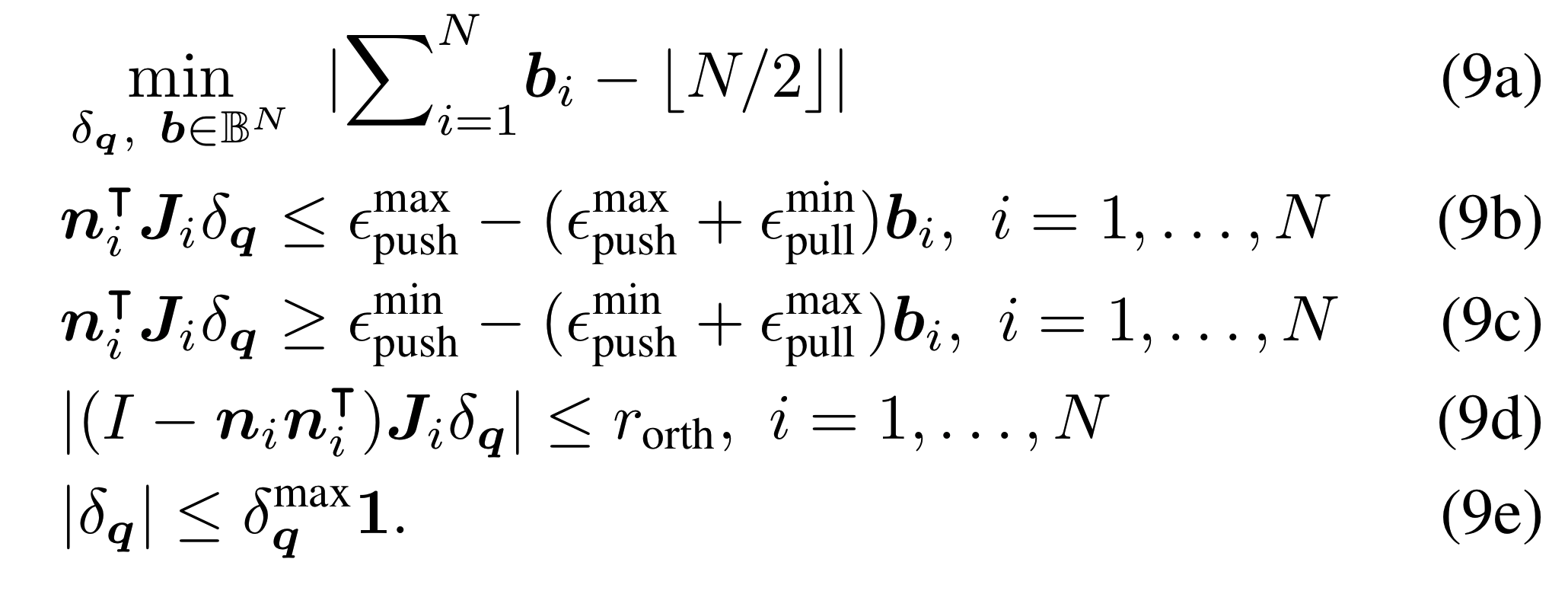
Total number of contacts.

Normal and Jacobian at contact \(i\).

Push/pull at contact \(i\).

Constrains sideways motion.

Small motion.

Take-aways

  • Detecting contacts from \(\bm{\tau}_\text{ext}\) on multiple links is probably not reliable in practice. 
    • Needs low-noise, unbiased estimate of \(\bm{\tau}_\text{ext} \).
    • Can be ambiguous even in the single contact case. 
    • Cannot handle more than one contacts simultaneously.
  • Tactile skin is perhaps the better solution?

How well does this work?

No. Tests Gradient Descent successes* Success% RDGD
successes		 Success%
CPF succeeds  7551 7326 97%
CPF no detection 916 874 95%
CPF too far away 1365 1112 81% 1255 92%
  • * Success means the true contact location is within 1cm of at least 1 of the samples gradient descent converges to.
  • 50 gradient descents are run on each link, with number of iterations capped at 100.

Failure modes

  • Many of the failures are due to anomalies in the mesh: "grooves (test 9701) and ledges". 

    • Improve mesh quality.

  • Some are due to failures in proximity queries

    • Use signed distance field instead of bounding volume hierarchy?

Flipped normal

test id 4838

Proximity query returns a point "off-mesh".

test id 510

True contact on a "ledge", not covered by samples. Therefore the local minimum doesn't exist on the robot surface.

test id 868

Find all local minima of \(l(\cdot; \bm{q}, \bm{\tau}_\text{ext})\) with Rejection Sampling + Gradient Descent (RSGD)

  • \(P_\delta\): set of accepted samples.
  • \(P_\delta^*\): set of optimized samples.
  • Accepted / all samples: 172/1000
  • Link  5 ,  converged_samples / accepted samples: 78/84
  • Link  6 ,  converged_samples / accepted samples: 80/88

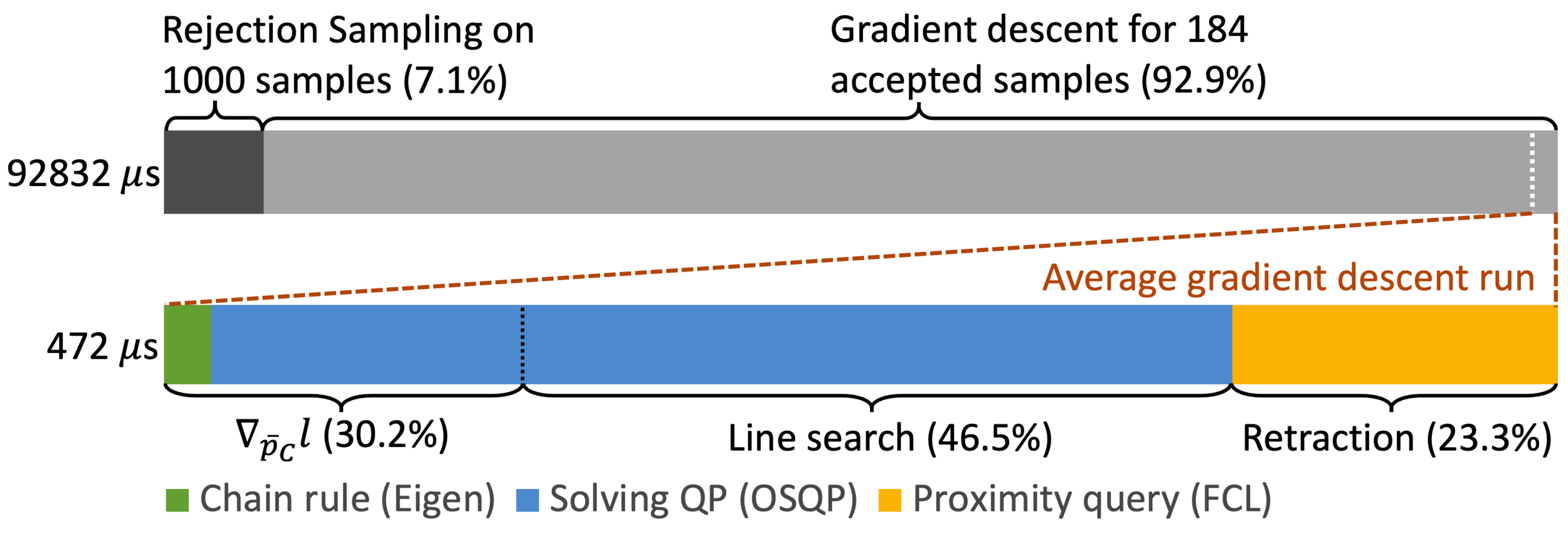
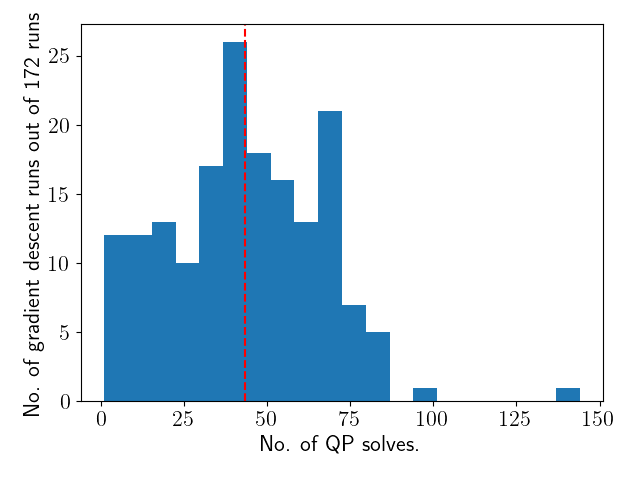
Average Number of QP solves per gradient descent: 43.4.