iRS-RRT
Pang, Terry, Lu
the Story
Q: how do we solve long horizon, planning through contact problems?
- Deep learning is impressive. But learned policies do not generalize to different tasks.
- So far, methods based on physics models suffer from the huge number of contact modes.
- Contact modes manifest as complementarity constraints in trajectory optimization. They can be mitigated with numerical tricks, but in general are sensitive to initial guesses and cost tuning.
- For simpler systems, contact modes can be enumerated. Discrete mode planning and continuous state planning can be interleaved in a sampling-based planning algorithm. But this would not scale to tasks such as 3D dexterous manipulation.
- In this work, we propose to replace the reasoning about contact modes with their statistical summary into locally linear systems, which we call bundled dynamics.
- We show the power of bundled dynamics with some simple modifications to the standard kino-dynamic RRT.
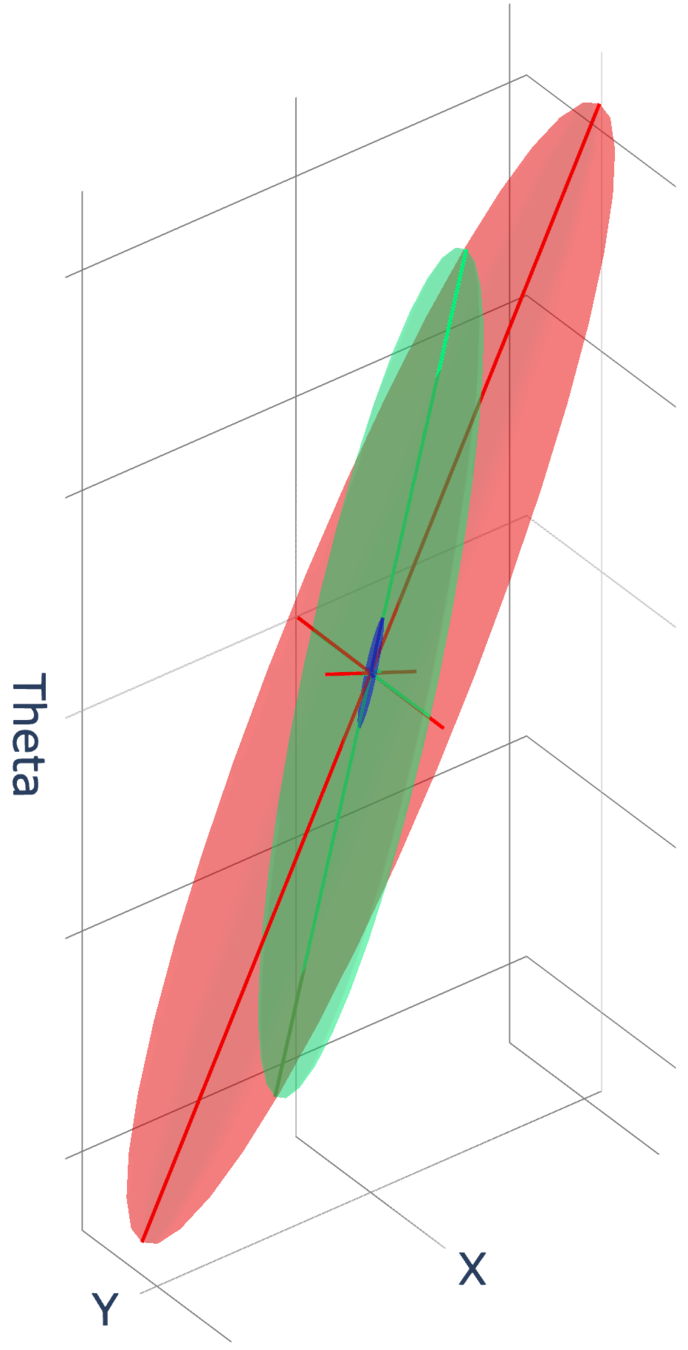
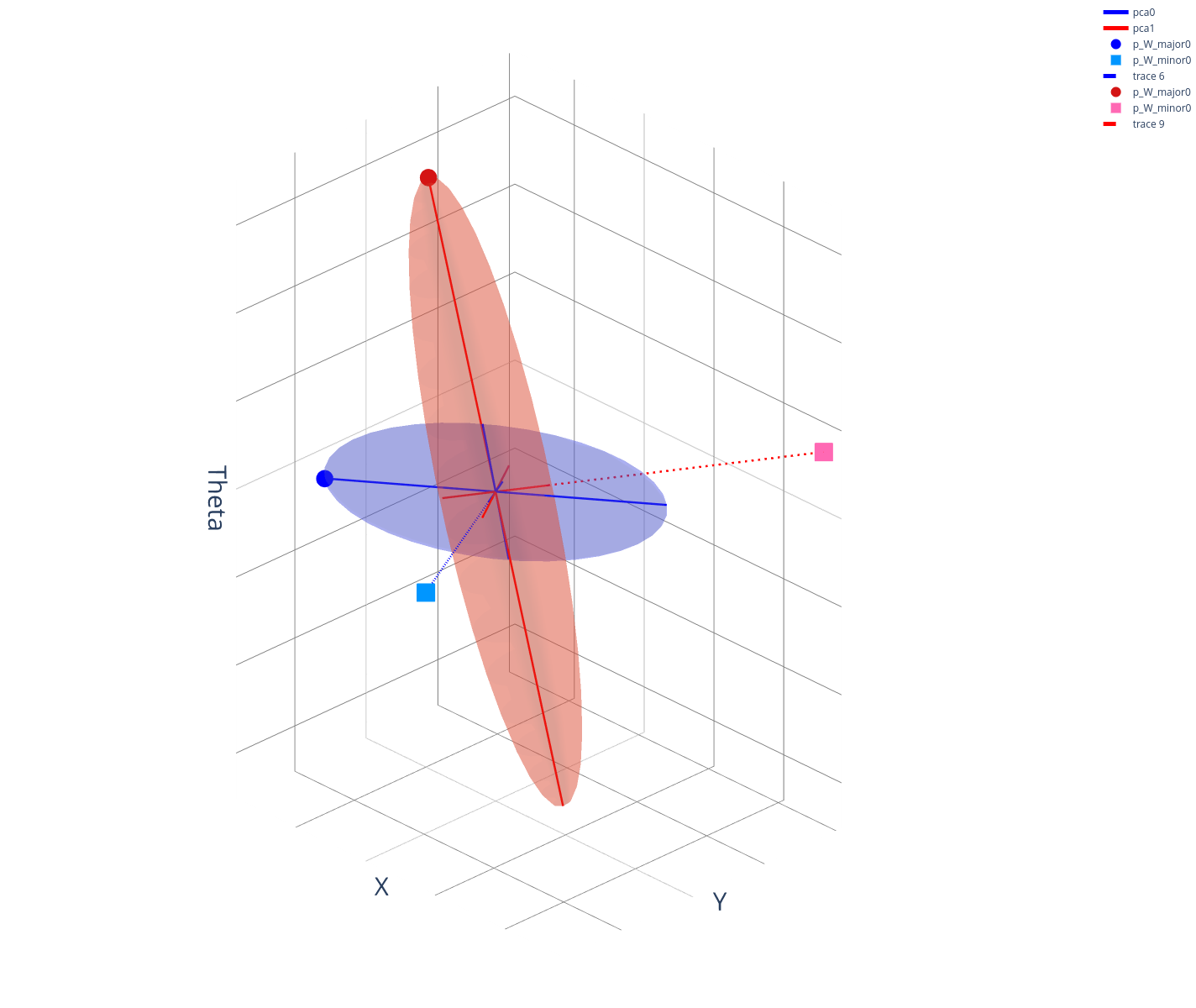
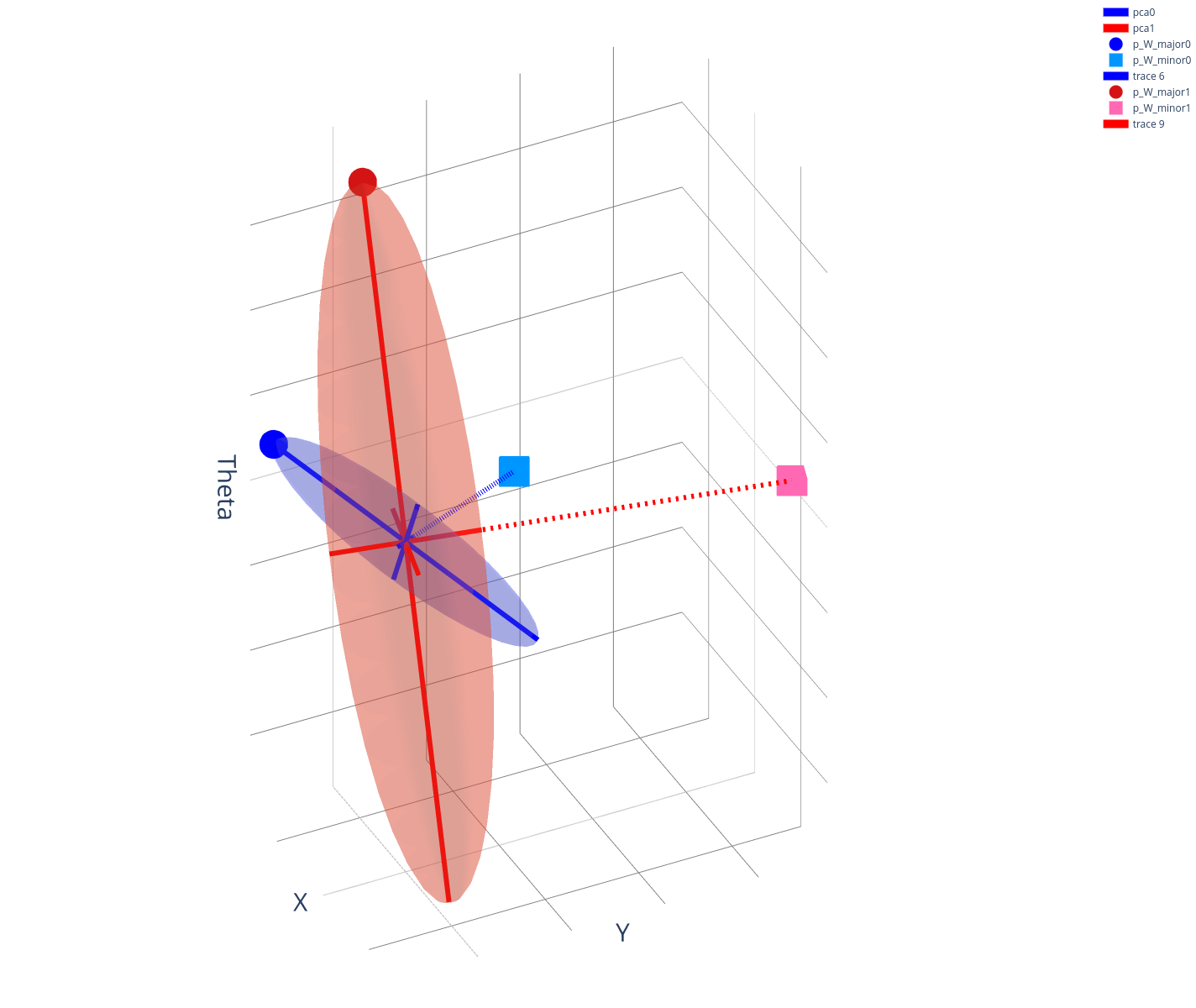
Reachable Set on Bundled Dynamics
Let's motivate the Gaussian from a different angle.
Recall the linearization of bundled dynamics around a nominal point.
Fixing the state, we reason about the states that are reachable under the bundled dynamics under some input.
(Image of the input norm-ball under bundle dynamics, assume \bar{u}_t is zero.)
The latter expression becomes the eps-norm ball under Mahalanabis metric.
Distance Metric Based on Local Actuation Matrix
Consider the distance metric:
This naturally gives us distance from one point in state-space another as informed by the actuation
(i.e. 1-step controllability) matrix.
NOTE: This is NOT a symmetric metric for nonlinear dynamical systems. (even better!)
Rows of the B matrix.
A is harder to reach (has higher distance) than B even if they are the same in Euclidean space.
Handling Singular Cases
What is B is singular, such that
The point that lies along the null-space is not reachable under the current linearization. So distance is infinity!
Numerically, we can choose to "cap" infinity at some finite value by introducing regularization.
Rows of the B matrix.
There is loss of 1-step controllability and A is unreachable. Infinite distance.
Connection to Gaussian Covariance Estimation
We can obtain the covariance matrix of the ellipse directly using gradient information, but we can also consider the zero-order version that solves the least-squares problem:
Under the least-squares solution, one can show a connection between directly doing covariance estimation on samples.
Consider putting the above into data matrix form
where X is data matrix of u that is sampled from zero-mean Gaussian and diag. covariance of sigma.
How bundled dynamics helps in kino-dynamic RRT
- RG-RRT uses local reachability information to guide subgoal sampling towards more reachable part of the smooth space.
- Bundled dynamics provides good reachability info for systems with contact.
- By helping with 1 or T-step trajectory optimization in extension (the same story as iRS-MPC).
- There's a trade-off between the number of nodes and the planning horizon T.
Rejection Sampling / Contact Sampling
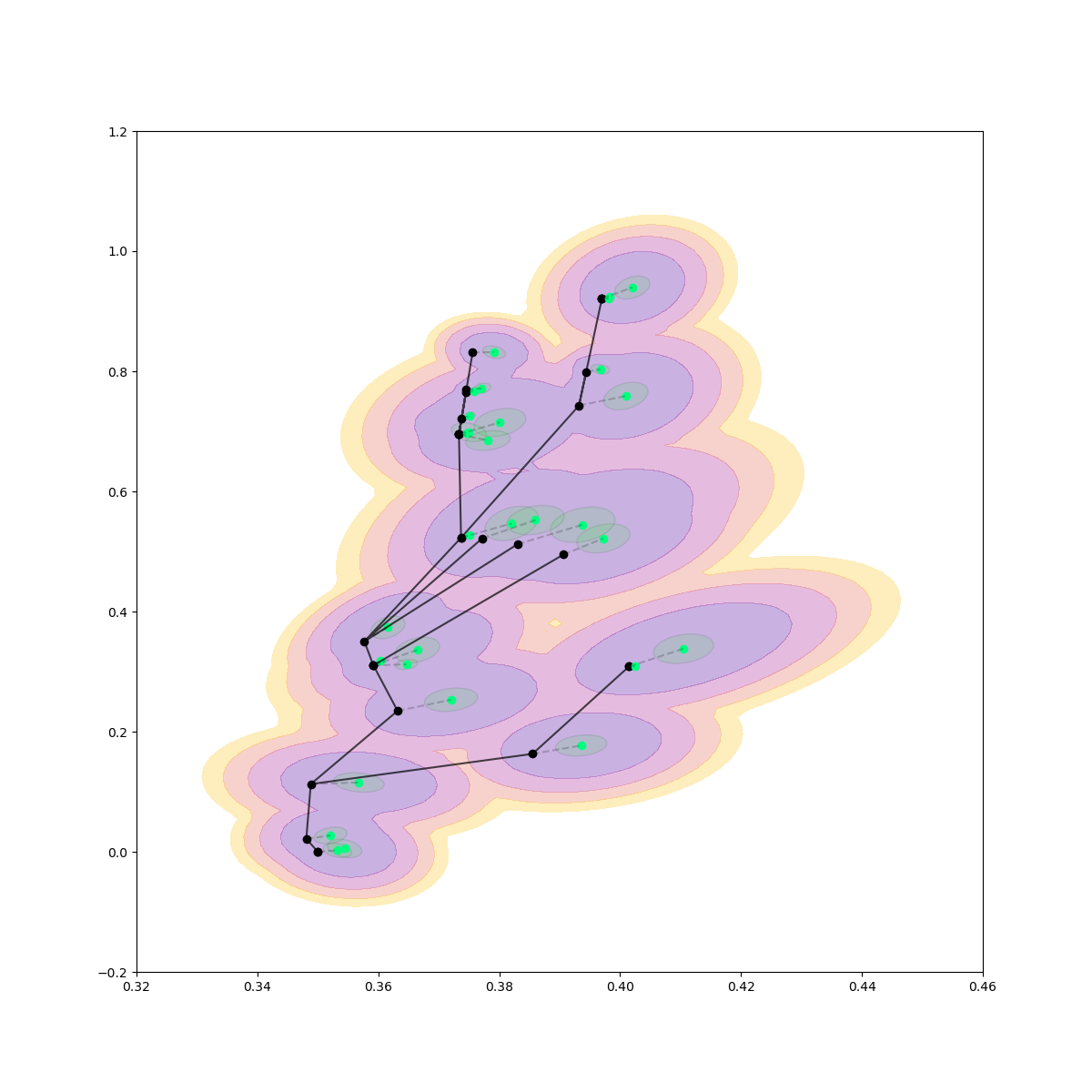
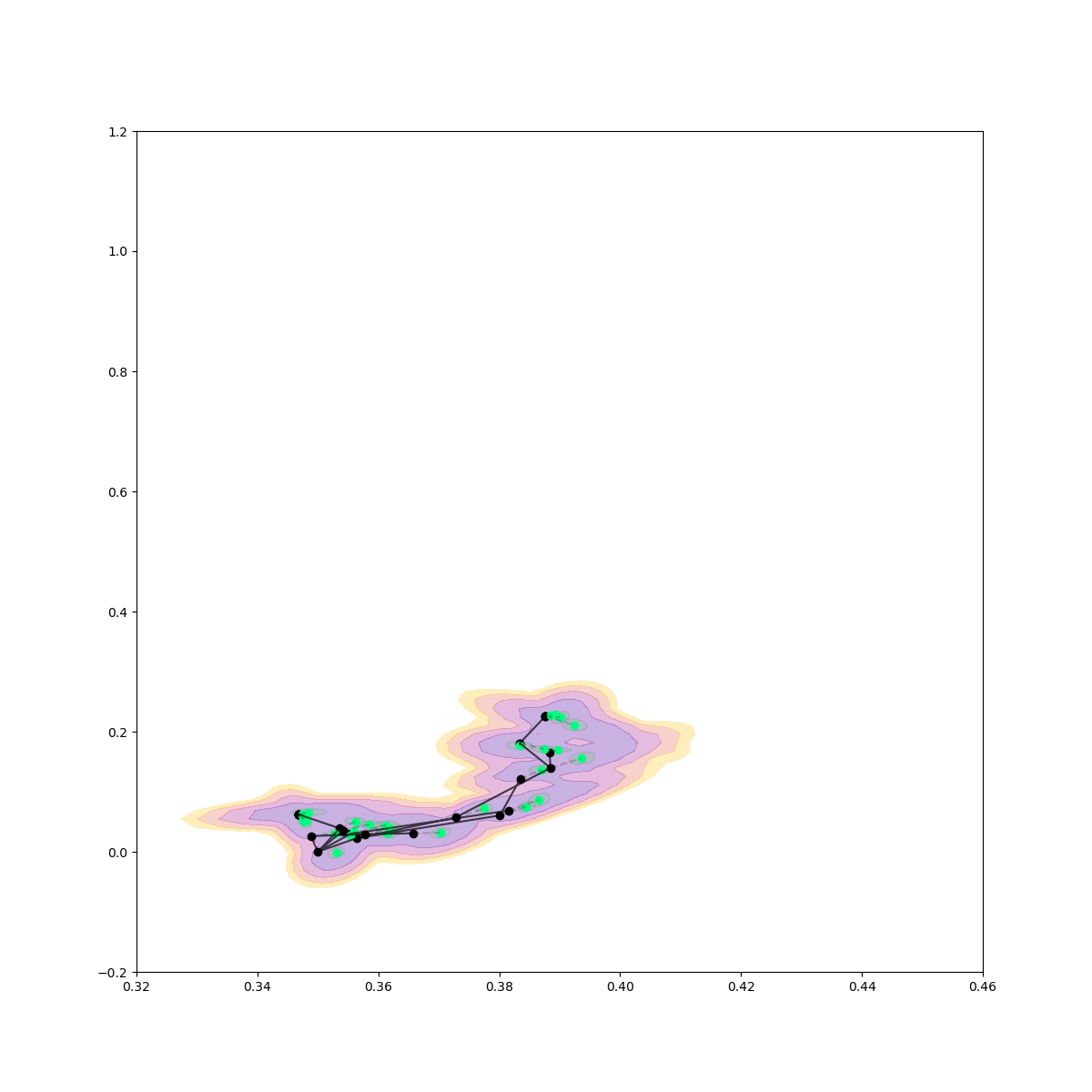
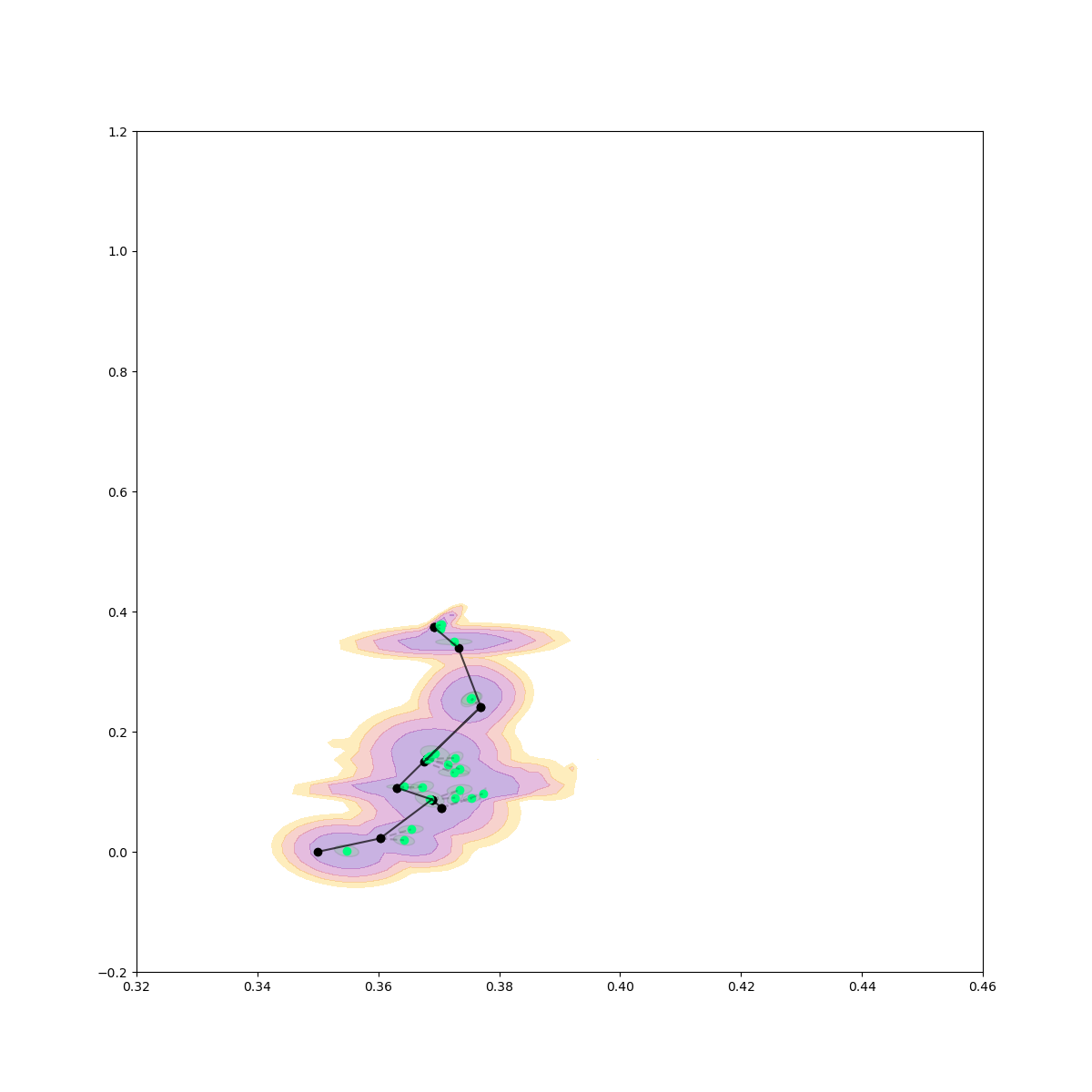
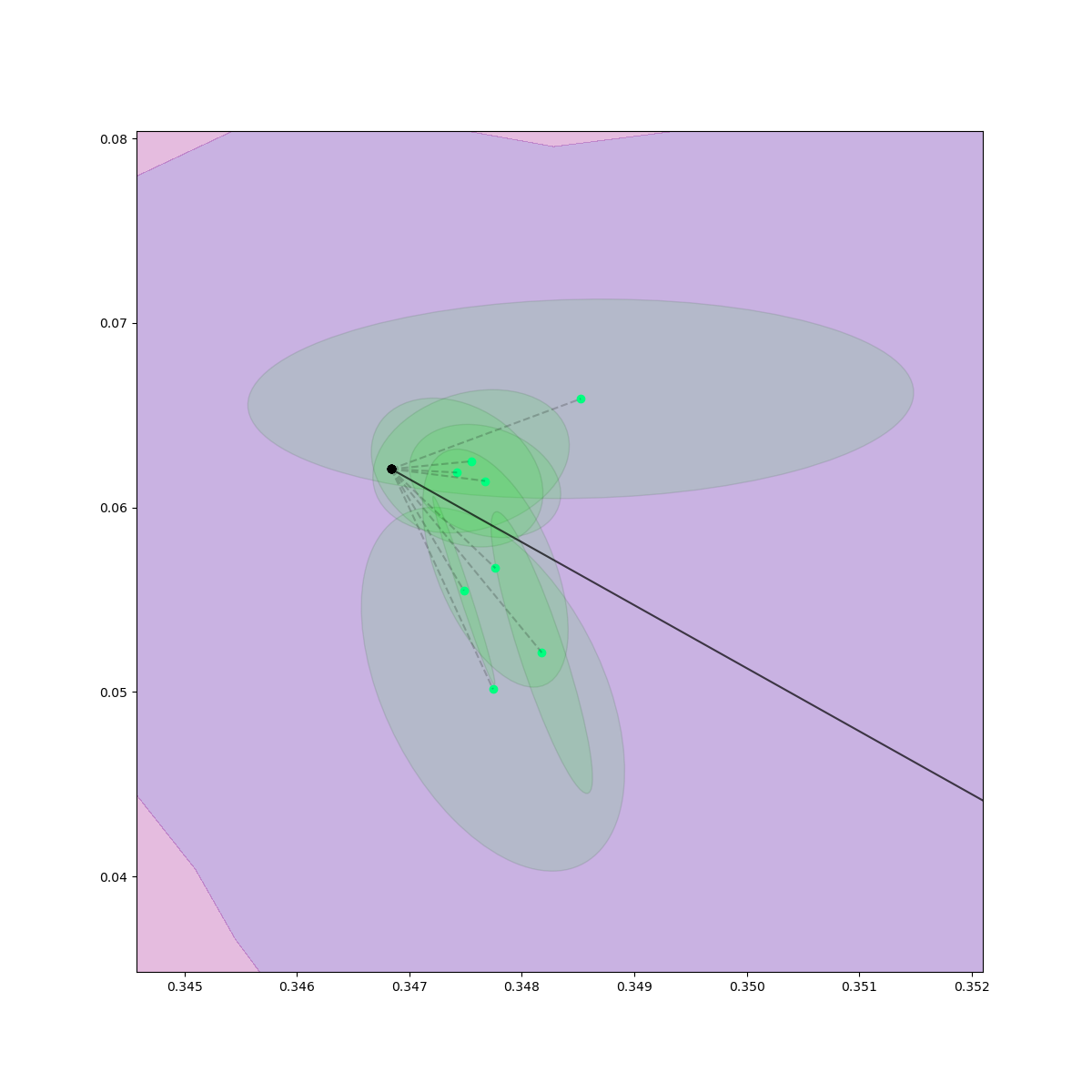
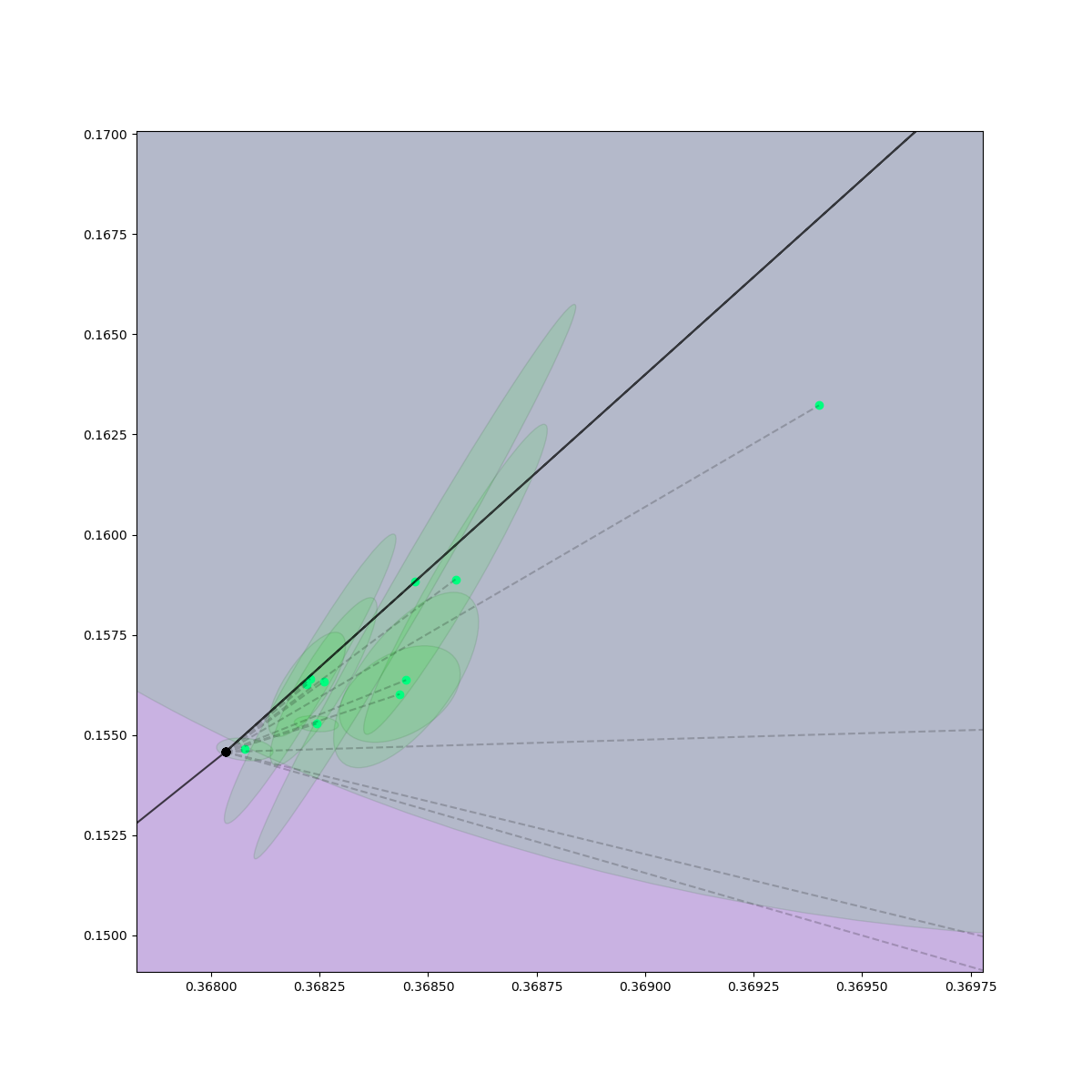
Rejection Sampling + Contact Sampling
No Contact Sampling
No Rejection Sampling
Results
- Planar pushing
- Planar hand
- Allegro hand
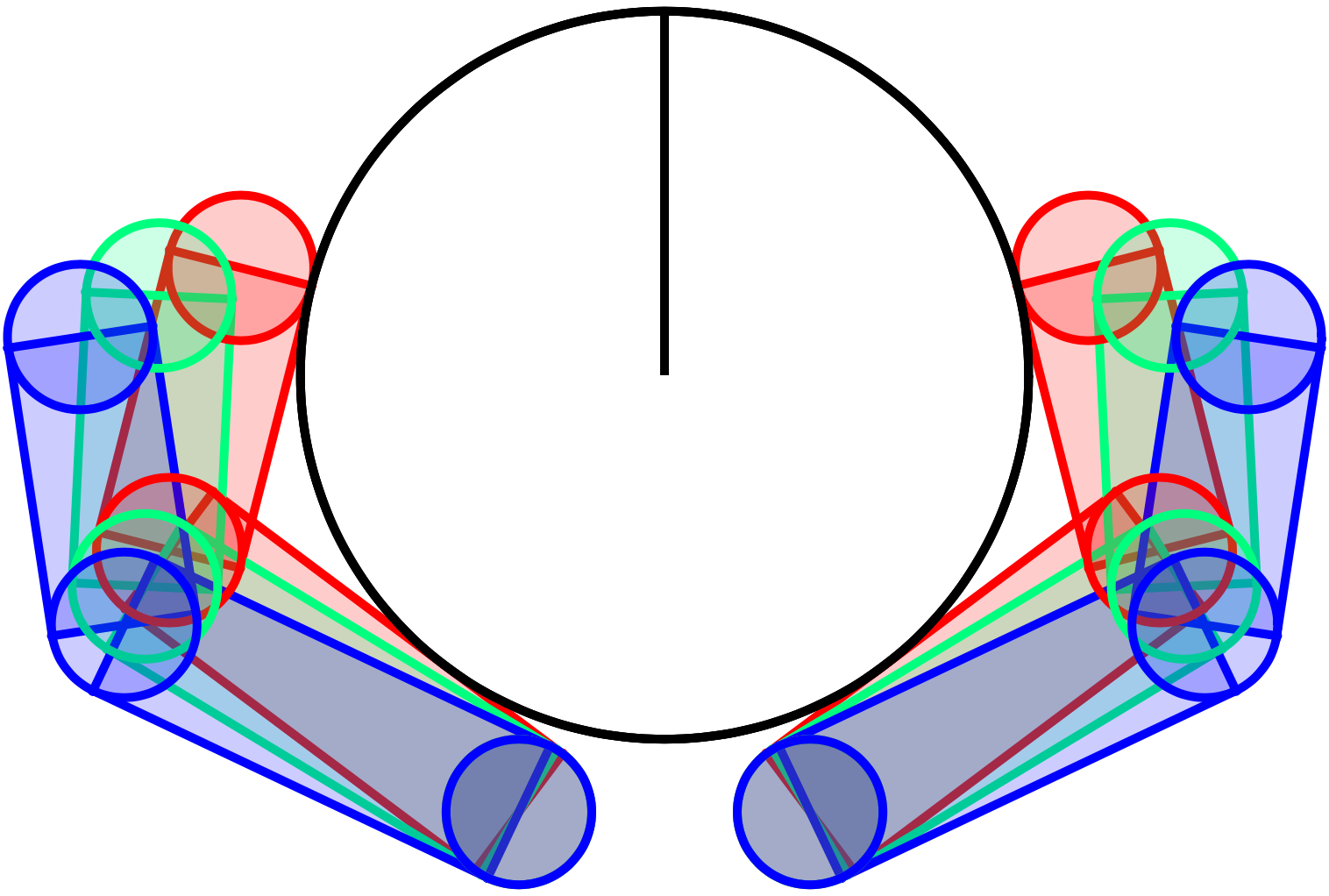
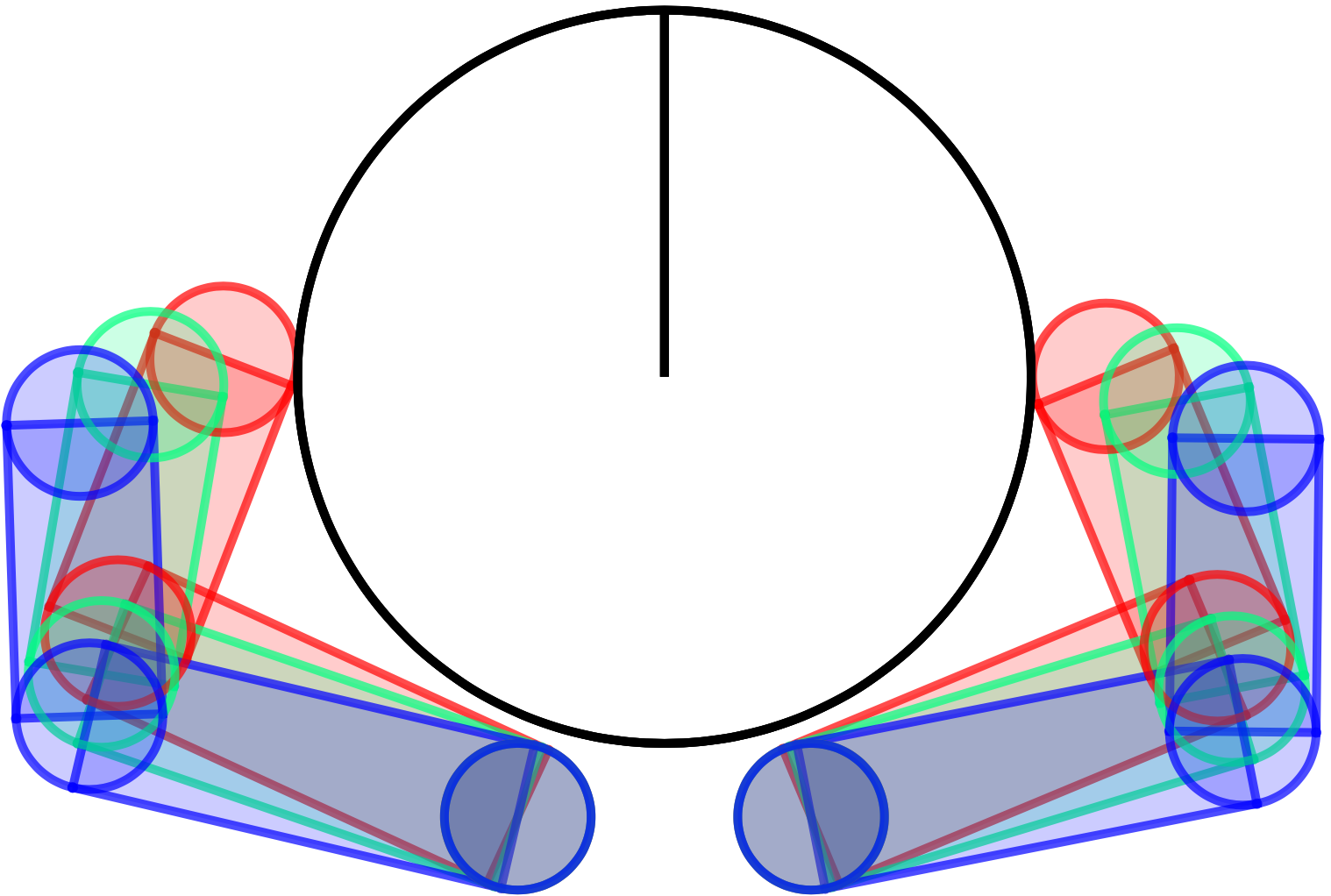
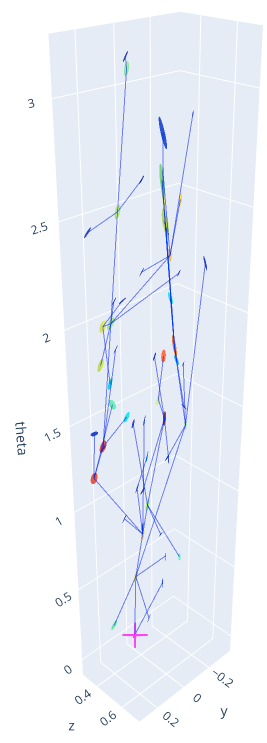
Planar Hand
1-step extension
20-step extension
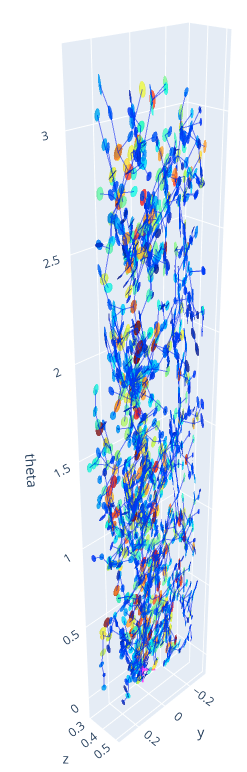
(b1)


(b2)
(b1)
(b2)
(c1)
(c2)
(c1)
(c2)
(a)
(b)
(c)
(d)
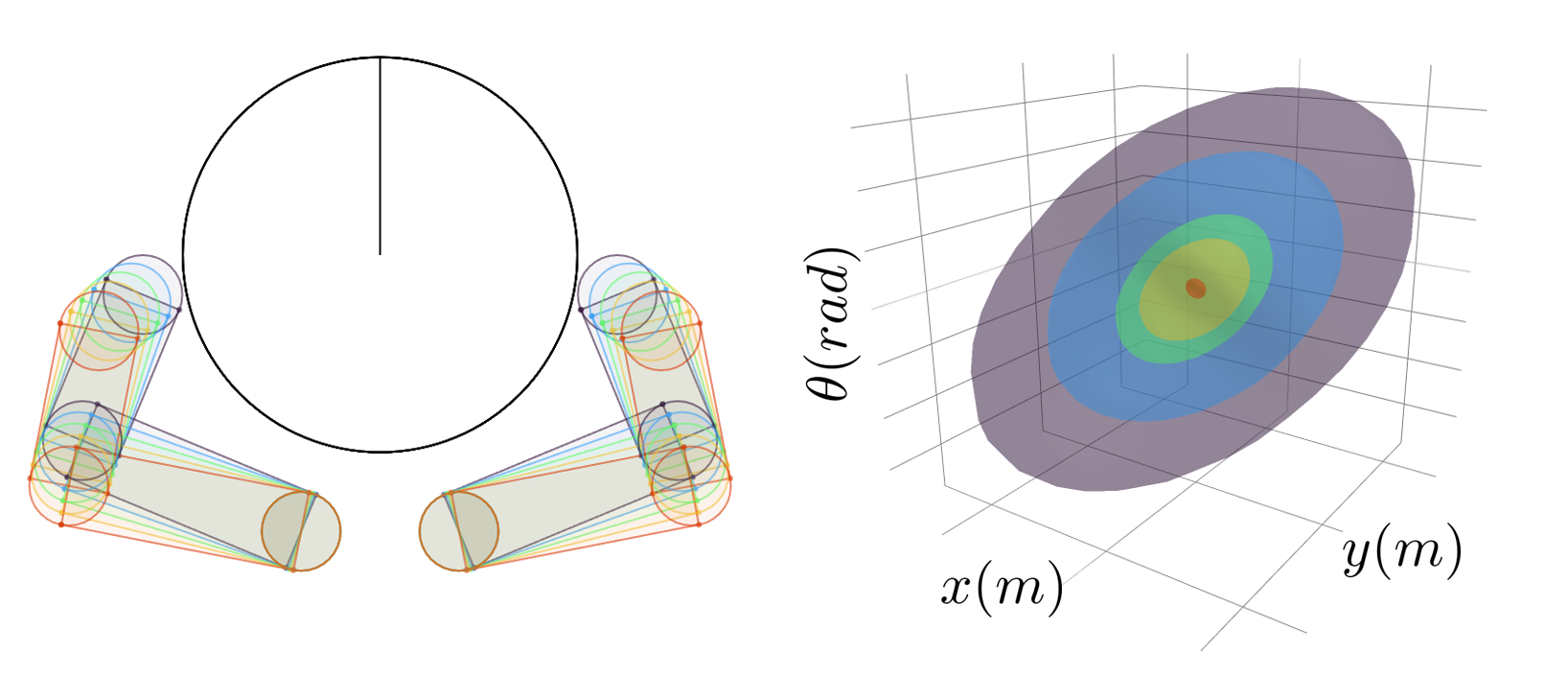



(a)
(b)
(c)



(a)
(b)
(c)

(d)


(a)
(b)
(c)

(d)