Simulation and planning using quasistatic models
Pang
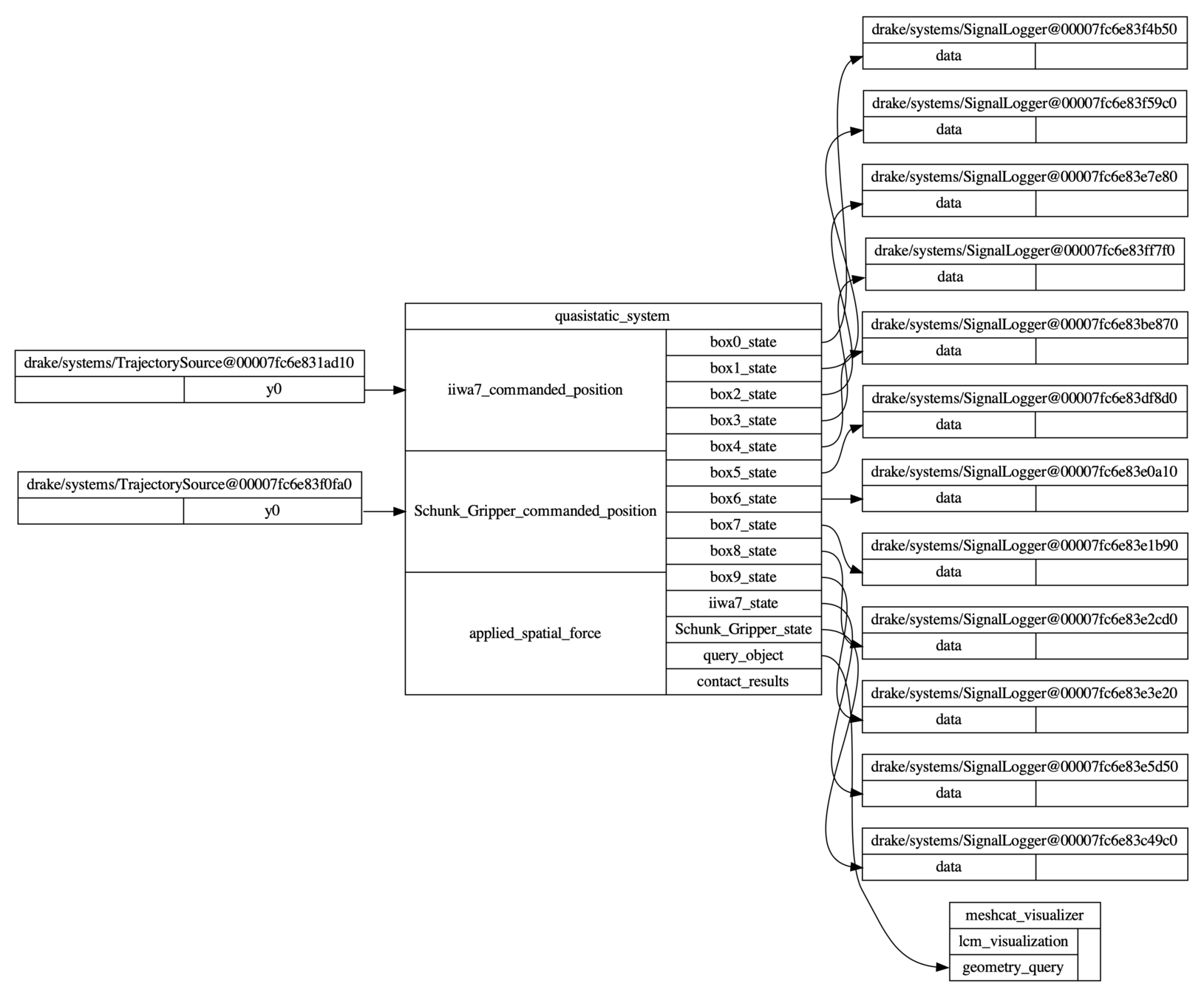
QuasistaticSystem(LeafSystem)
- A discrete-time system modeled after MultibodyPlant.
- Input ports:
- Commanded trajectories of actuated model instances.
- Applied spatial forces.
- Output ports:
- State (configuration) of all model instances.
- QueryObject.
- ContactResults.
- 5 unit tests.
- IIWA trajectory following.
- IIWA external loading.
- IIWA box pick-and-place.
- 3-link arm box pushing 2D.
- 3-link arm box pushing 3D.
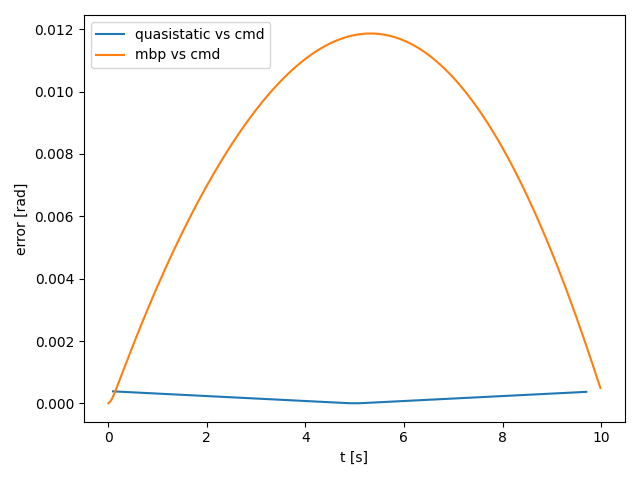
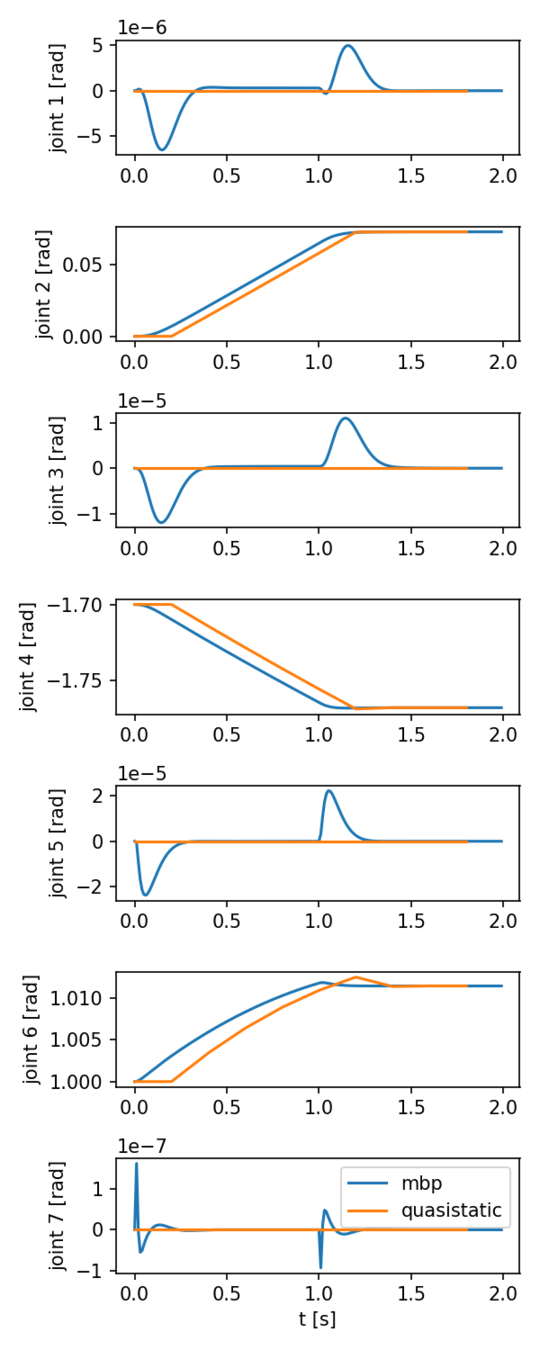
IIWA trajectory following
Quasistatic, h = 0.2s.
MBP, h = 1e-4s.
- IIWA is commanded to track a given trajectory. The robot is controlled with [this controller](https://github.com/pangtao22/iiwa_controller).
Comparison
- The two trajectories are almost identical.
- But the error between MBP and commanded is larger than that of quasistatic sim. And MBP always lags behind quasistatic.
- Increasing the duration of the trajectories means integrating smaller error over longer period of time, and the result seems to be constant total integral error.
- The difference between MBP and quasistatic be justified by the fact that second-order systems have non-zero steady-state error under ramp inputs.
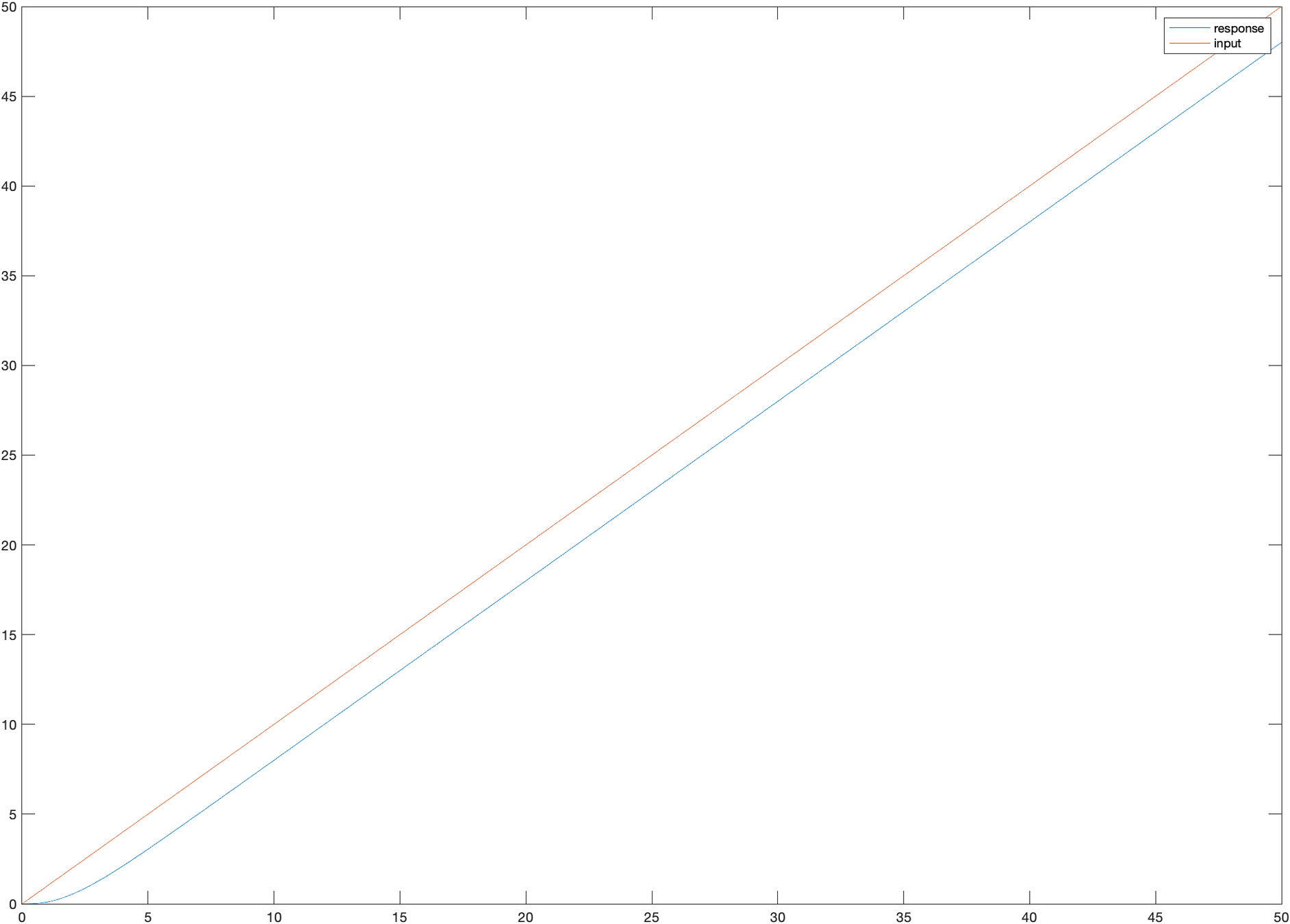
- Input: \( \frac{1}{s^2}\)
- System: \( \frac{1}{s^2 + 2s + 1} \)
IIWA external loading
- An external force is applied to the origin of link 7. The force has constant direction [0, 0, -1]. Its magnitude is increased from 0N at t=0s. to 100N at t = 1s.
- Quasistatic and MBP simulations have the same final joint angles.
- h_quasistatic = 0.4s. h_mbp = 1e-4s.
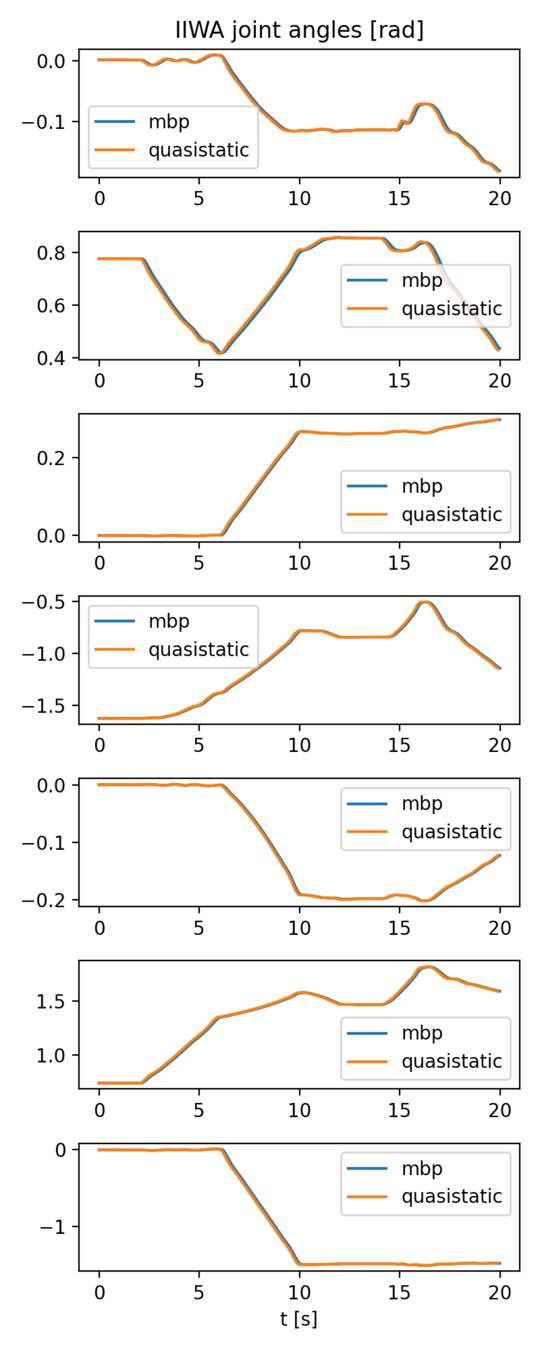
IIWA block pick-and-place.
Quasistatic, h = 0.1s.
MBP, h = 1e-3s.
- IIWA is commanded to track a given trajectory, which picks up the red box and places it on the pile in its front.
- The robot is controlled with [this controller](https://github.com/pangtao22/iiwa_controller).
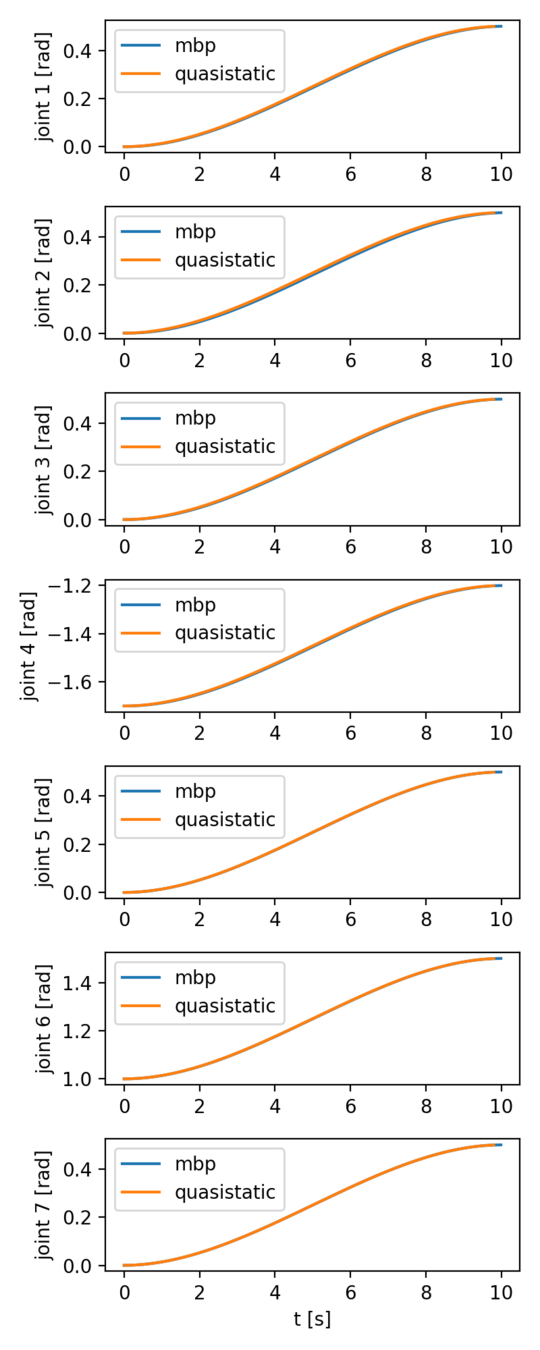
IIWA comparison
- Robot trajectories (right) are almost identical, with a small lag observed in MBP.
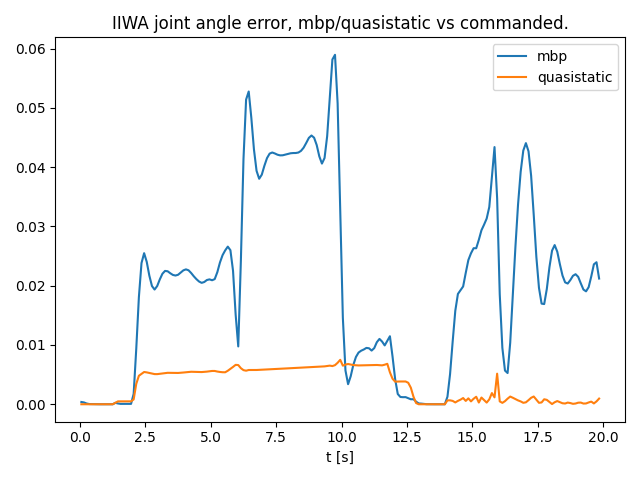
- Error between MBP and commanded is larger than that of quasistatic.
- Spikes in MBP tracking error correspond to acceleration/deceleration of the red block.
Red box comparison
- The quasistatic model should be following the "commanded" trajectory more closely, as there is no lag due to inertia.
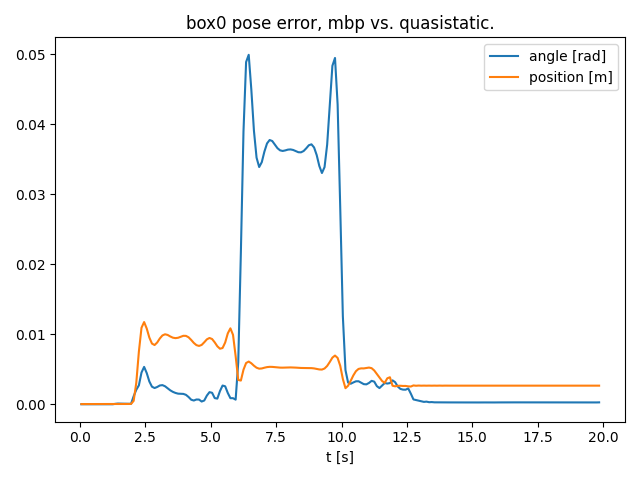
Spikes due to acceleration/decelration.
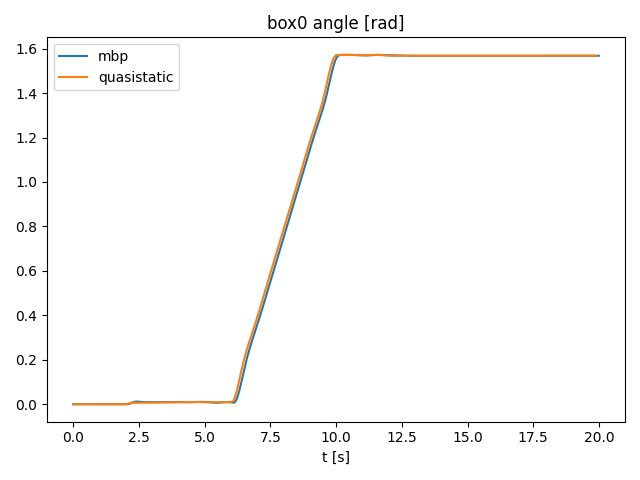
3 link arm block pushing 2D
Quasistatic, h = 0.1s.
MBP, h = 1e-3s.
- The 3-link arm pushes a robot constrained to the yz plane.
- The robot is controlled with [this controller](https://github.com/pangtao22/iiwa_controller).
Comparison
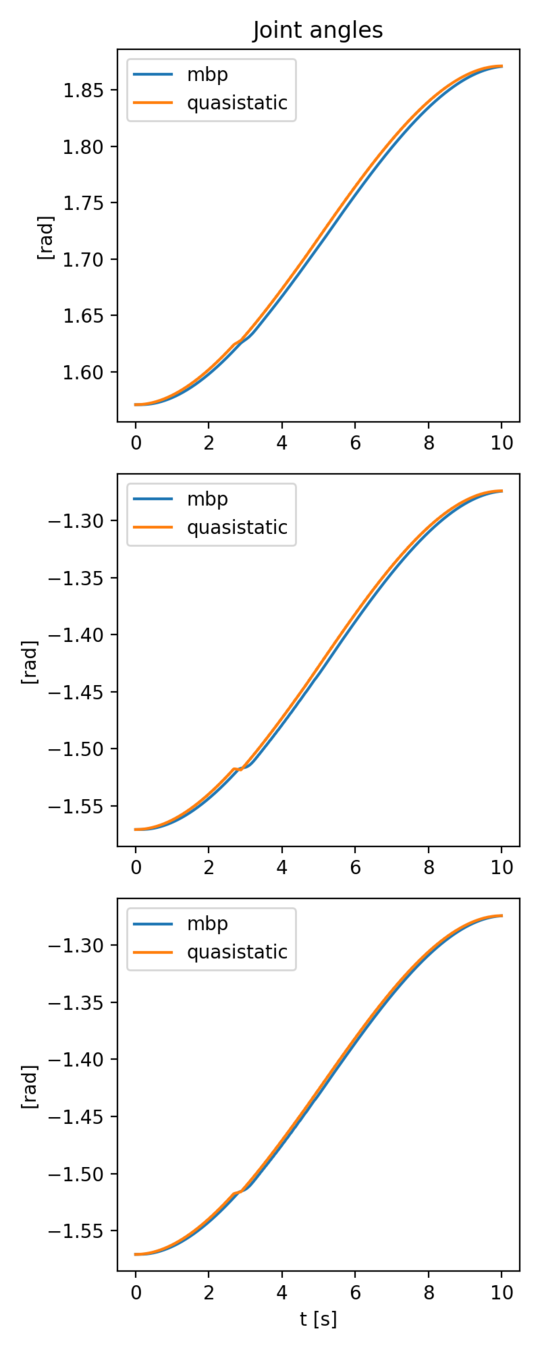
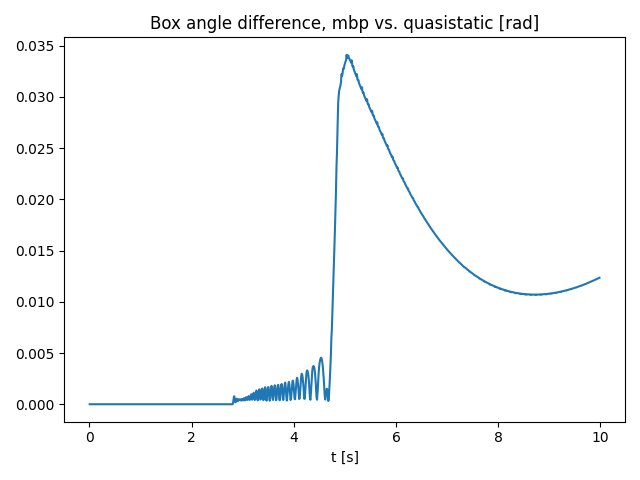
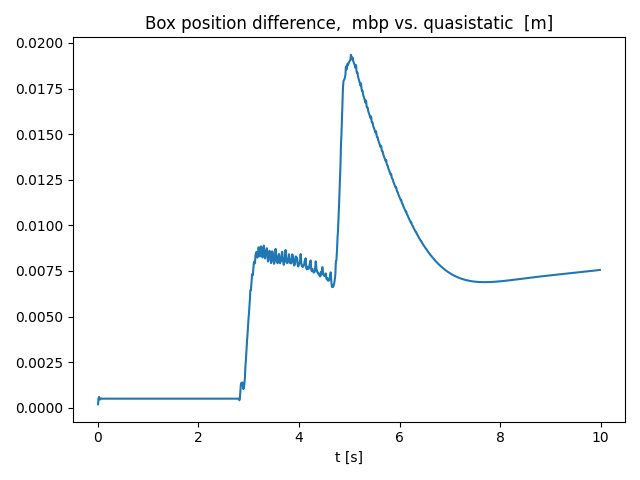
3 link arm block pushing 3D
Quasistatic, h = 0.1s.
MBP, h = 1e-3s.
- The 3-link arm is commanded to push a box in 3D.
- The arm is controlled with [this controller](https://github.com/pangtao22/iiwa_controller).
- An example of "unstable pushing" that shows the difference between contact models.
- The box starts at symmetric about the yz plane.
- The box in MBP remains parallel to the yz plane.
- The final pose of the box in quasistatic sim appears to be non-deterministic! (will investigate.)
Box turns left.
Box turns right.
Comparison
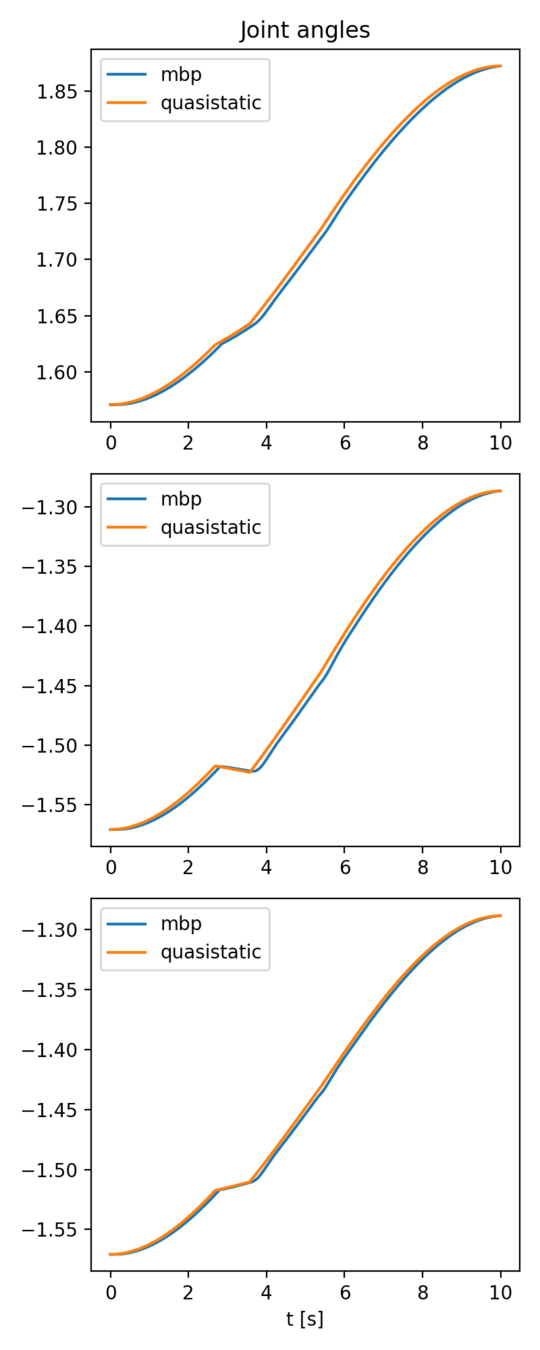
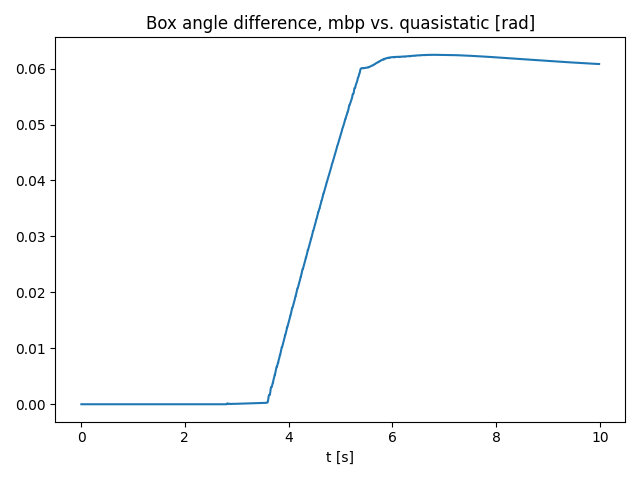
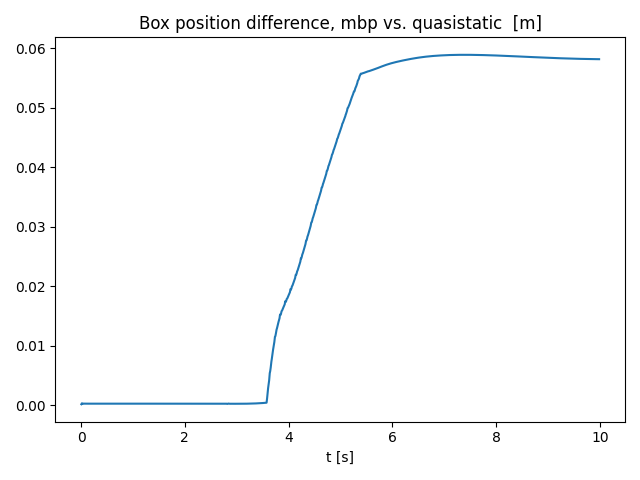
- The difference starts to grow as the box starts to slide.
Uniqueness
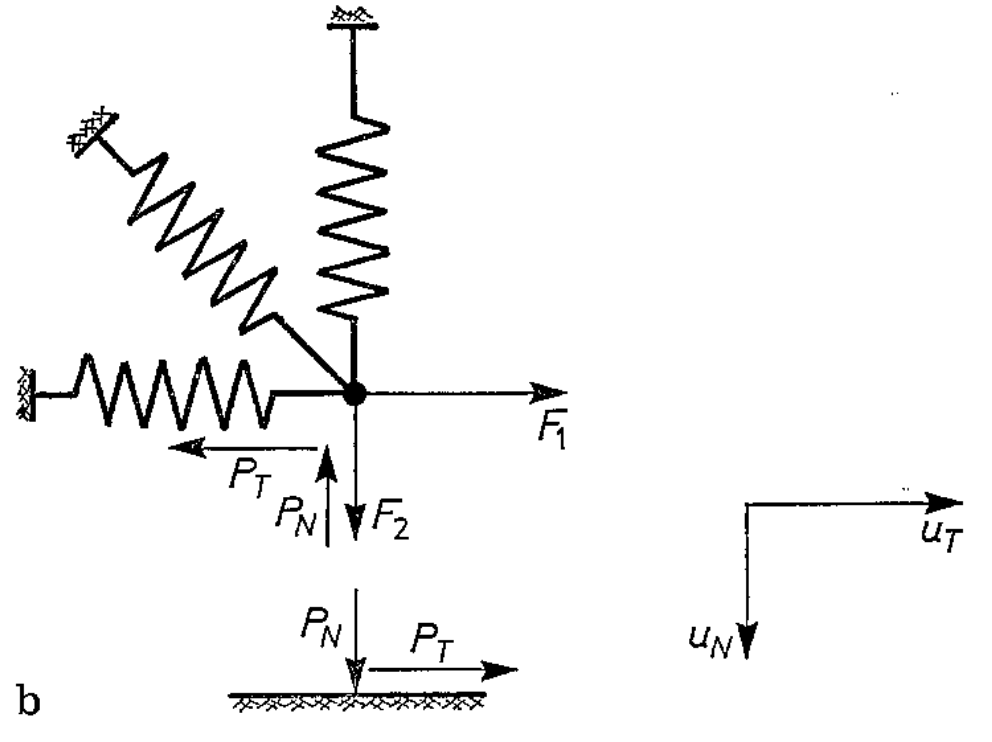
- The motion "should" be unique if the frictionless system is statically determinate and the friction coefficient is moderate.
- There are corner cases in the LCP model:
- Even for a single contact point, there exists contact point stiffness which leads to multiple contact modes being feasible at the same time.
- There must be similar corner cases in Anitescu's model, but I haven't tried very hard to find them.
- I'll look at the planning problem first and think about uniqueness along the way.
Klarbring, A. "Examples of non-uniqueness and non-existence of solutions to quasistatic contact problems with friction." Ingenieur-Archiv (Archive of applied mechanics) 60.8 (1990): 529-541.
Title Text
- Bullet One
- Bullet Two
- Bullet Three