Planning through contact for dexterous manipulation

Pang

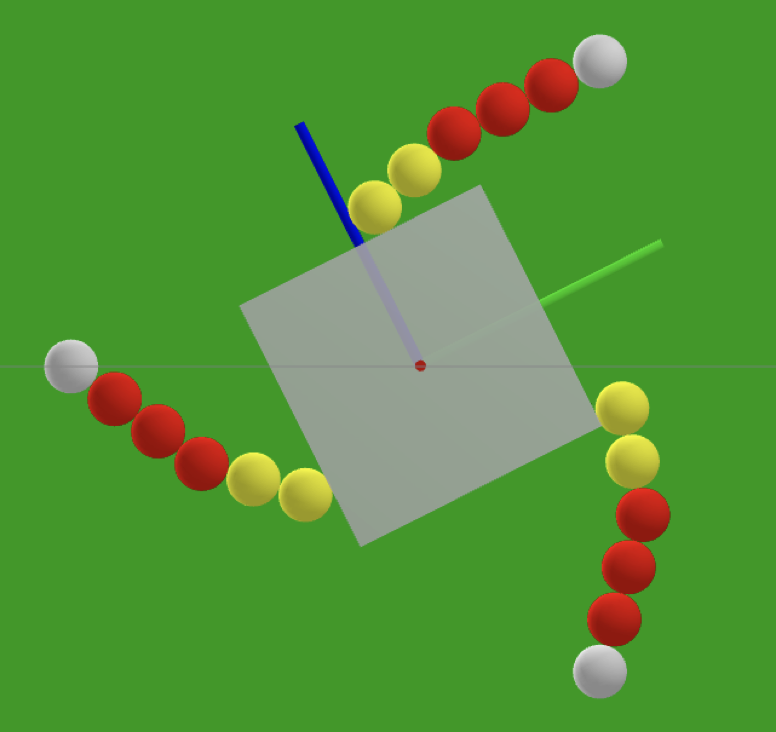
Simple model to start with

Goal

Inspiration

Contact as logical decisions

  • Making a contact or not has significant consequence on the outcome of an action.
  • The consequences can be modeled using binary-variables or complementarity constraints.

Throwing a ball at a wall

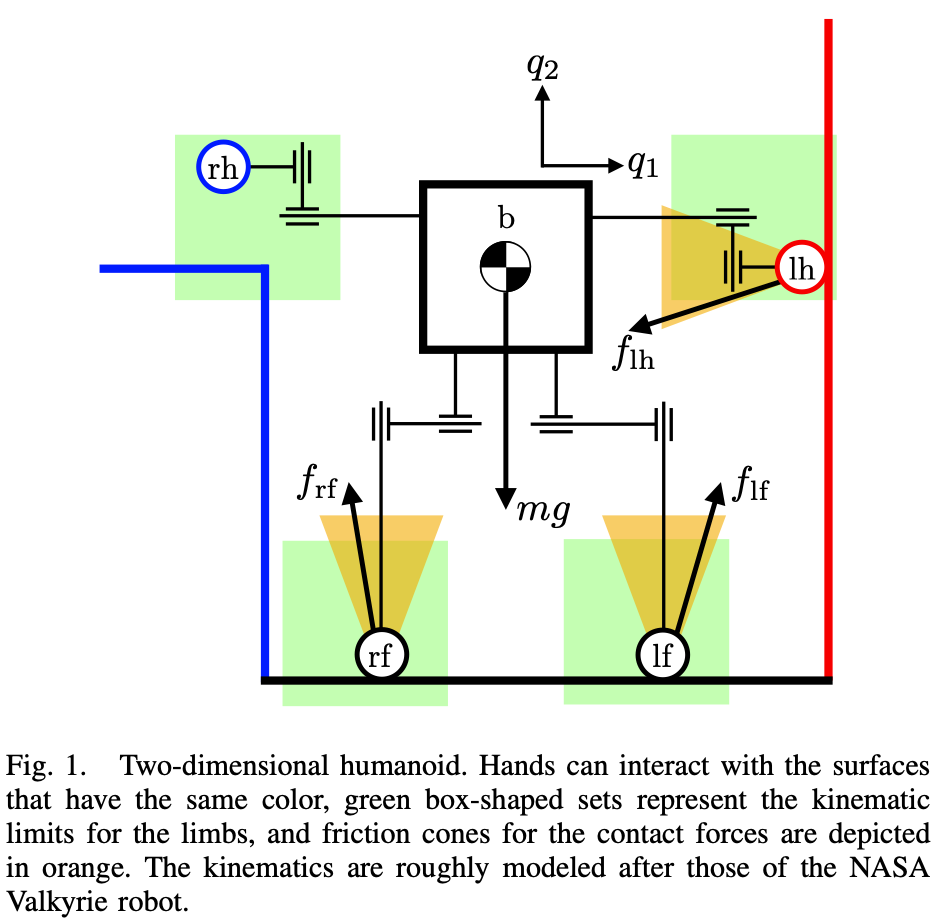
Humanoid push recovery

Marcucci, Tobia, et al. "Approximate hybrid model predictive control for multi-contact push recovery in complex environments." 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids). IEEE, 2017.

Tedrake, Russ "Underactuated Robotics." http://underactuated.mit.edu

  • Actions in maze and Klotski have a similar flavor, which is probably why mixed-integer approaches are effective at solving them.
  • But I think not all contacts in dexterous manipulation are logical decisions.

Example: rotate a box by 90 degrees in my hand.

Start

Move fingers to grasp.

  • Red: grasping fingers.
    • high stiffness.
  • Blue: passive fingers.
    • move along grasping fingers to avoid collision.
    • keep the object caged to reject potential disturbances.
    • low stiffness to minimize potential hinderance of object motion.

Rotate the object with standard, robotic in-hand manipulation.

Re-grasp, as some fingers have reached joint limits in (3).

(1)

(2)

(3)

(4)

(5)

The manipulation action transitions from grasping to caged pushing between (4) and (5).

  • Yellow: pushing fingers.
  • Green: stationary finger which constrains the motion of the box.

Some contacts are more important than others.

  • Contacts between the object and the active fingers (grasping, pushing) are important.
  • Contacts between the object and the passive fingers and the palm can be treated as disturbances, and compensated for by higher stiffness of the active fingers.

The primitives (grasping, pushing) have counterparts in robotics, but it's hard to predict when to switch primitives except in simulation (learn when to switch!).

Random thoughts on contact in dexterous manipulation

Our current models for contact (mixed-integer or complementarity constraints) treats every contact, or even every extreme ray of every friction cone, as equally important logical decisions. This makes the problem artificially harder.

In the correct action space, planning for most dexterous manipulation tasks should be simple. 

  • I don't think I was solving a maze when I re-oriented the box in my hand.
  • Instead, I was simply switching between a handful of basic skills (primitives?) and doing very naive (greedy?) planning.
  • Switching between primitives are needed usually when fingers (robots) reach joint limits or Jacobian singularities.

Proposed planning algorithm: connecting primitives (again!)

  • Primitives come with good controllers:
  • Compared with mixed-integer/contact-implicit trajectory optimization, primitives do limit the range of behaviors that can arise from making contacts, but I believe moving objects from pose A to pose B in 3D can be done with just a handful of primitives.

In-hand manipulation

Stable pushes

...

Contacts beyond end effectors

My work

Proposed planning algorithm: connecting primitives

  • Sample primitive (grasp).
  • Sample contact locations.
  • Solve collision free IK to get to the new contact locations.

Task: rotate the box by 90 degrees with robots.

Move greedily towards the goal, 

until the current primitive is not "good" anymore. 

Repeat until goal is reached.

Signals for the "goodness" of primitives are abundant, and easy to evaluate in simulation.

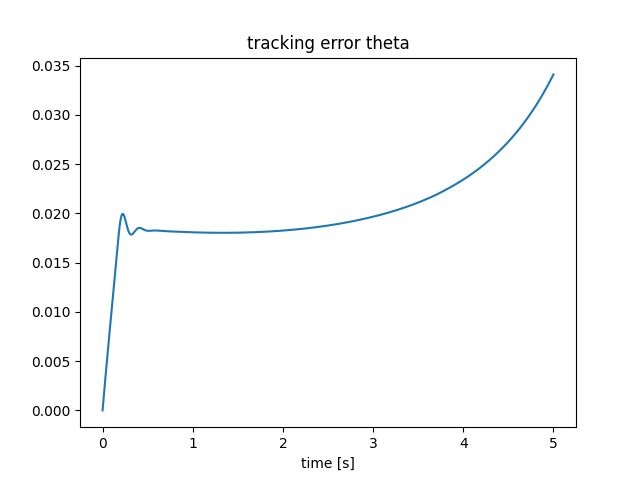
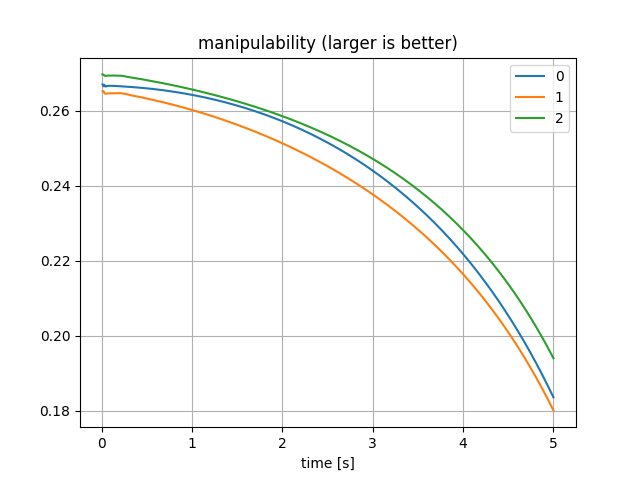
Rephrasing the planning algorithm using the language of RL.

  • State \(s\): \((q_u, q_a)\), object pose and robot joint angles.
  • Action \(a\): (primitive type, contact points, \(\Delta q_u\))
  • Reward \(r(s, a, s')\): can be computed from forward simulation.
    • Exists collision-free path to the new contact points?
    • Distance to goal pose
    • Manipulability
    • tracking error (rate)
    • area between grasping points
    • distance to corners
    • etc.

 

  • The planning algorithm described on the last slide is Monte-Carlo tree search (my quasistatic simulator may make it faster!).
    • This should be enough for an OpenAI-style (reaching 50 different poses in one shot) demo with 2 IIWAs and one box!
  • We can throw AlphaGo tricks at this problem to make it faster:
    • learn policy/value/Q/reward function to get high-reward actions quickly without rollouts.
  • We can also throw Yunzhu's network pruning algorithm at the learned value/Q function.
    • Better understand the decision surface?  

Previously...

  • Dexterous manipulation tasks can be accomplished by connecting primitives.
    • A primitive consists of
      • \(p_{C_i}, n_i\): contact points and normals
      • \(q_a\): robot joint angles to establish contacts.
      • \(\Delta q_u\): change in object pose.
  • The primitives are "good" only locally.
    • Their quality deteriorates as \(\Delta q_u\) grows.
    • This can be quantified by signals such as manipulability of the robots.
p_{C_1}
p_{C_2}
p_{C_3}
n_1
n_2
n_3

Sampling-based Planning

\( q_u = q_{u_0} \)

while \(|q_u - q_{u_{\text{goal}}}| < \epsilon \)

    while True:

        SamplePrimitive: \((p_{C_i}, n_i, q_a, \Delta q_u)\)

        if primitive_quality > threshold:  # primitive quality evaluated with rollout

            break

    \(q_u \) += \( \Delta q_u\)

------------------------------------------------------------------------------------------------------------------

An RRT version of this could also work.

p_{C_1}
p_{C_2}
p_{C_3}
n_1
n_2
n_3
  • Evaluate primitive quality with rollouts can be expensive. 
  • Propose to learn
    • a policy from \(q_u, q_a\) to primitives.
    • f(primitive, object_geometry) -> primitive quality
      • so that low-quality primitives can be rejected quickly without rollout. 
  • ​Hypothesis:
    • For "similarly-shaped" objects, the quality of a primitive only depends on the local geometry of the object and the robot geometries.
      • It does not bake in the global geometry of the object.
      • Local geometry can be estimated well with tactile sensors.
    • The learned primitive quality function can generalize to other objects.
  • Demo: robots manipulating arbitrary objects thrown at it through contacts.