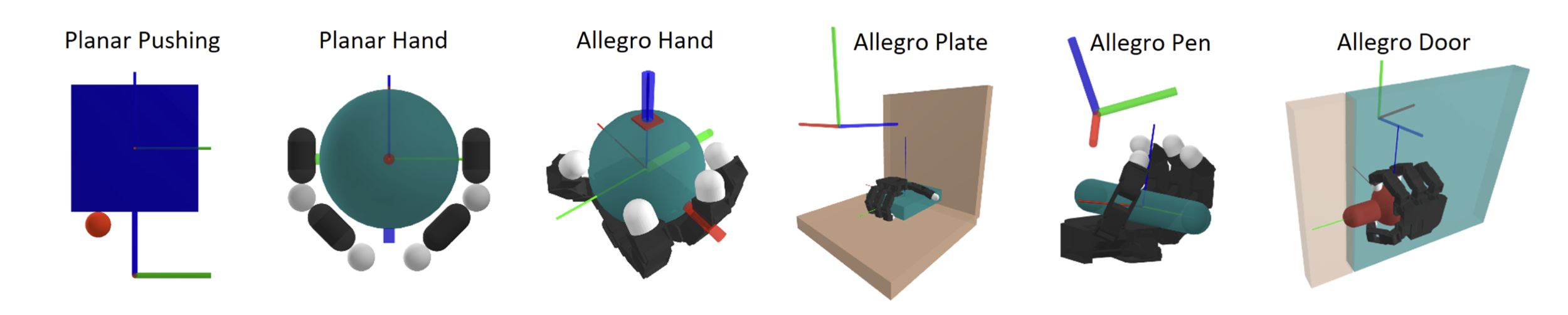
Why contact-rich?

Collision-free Motion Planning

Interact with the world

Collision-free Motion Planning

But this is excessively restrictive!

Why contact-rich?

Box

What if we have a larger box...?

We need to use a bigger arm...

Or make more contacts!

Why contact-rich?

A few more arms

Smaller

Contact-rich planning and control can enable both bimanual whole-arm manipulation and dexterous manipulation.

Why don't we do RL (reinforcement learning)?

Impressive demo of in-hand re-orientation, but...
Excessive offline computation.
The learned policy
- does not generalize (to e.g. opening a door),
- is hard to interpret.

2018

Model-based Planning through Contact: a Quick Review

2014

Nonlinear optimization with
- Lagrangian dynamics constraints.
- Complementarity constraints for frictional contacts.

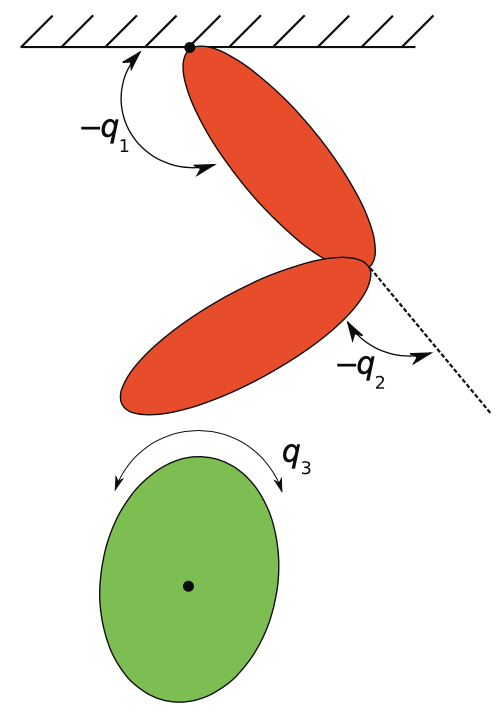
Take aways:

Traj-opt through contact suffers from local minima, like all other trajectory optimization algorithms.
PWA + MIP scales poorly with the number of contacts.

2017

Model: Piece-wise Affine Systems (PWA)
Method: Branch and Bound for Mixed-Integer Programming (MIP)

2021

PWA along a nominal trajectory: fewer pieces.
Method: specialed ADMM solver for MIP.

But slows down to 16Hz for a more complex system:

2022: Our Method

RRT and Trajectory optimization for dexterous hands (>16DOF).
- RRT takes less than a minute.
- Trajectory optimization is fast, and only needs trivial initialization.

Open-loop execution of contact-rich plans:

Global PWA Formulation

Space of \(x_1\)

x_1

\dots

Space of \(x_T\)

x_T

Each piece has its own affine dynamics: \[ x_{t+1} = A_i x_t + B_i u_t + c_i, x_t \in \mathcal{D}_i \]
\( (x_0, \dots, x_T) \): a trajectory.

Space of \(x_0\)

x_0

\mathcal{D}_i

Discretize the entire state space and enforce PWA dynamics constraints with integer variables.
Even for linear dynamics and a handful of contact modes, solving the optimal control problem is already too slow for control.
Tobia knew there are too many pieces (for a different reason in a different space), and reduced the number of pieces by looking only for feasible solutions (very roughly speaking).

Local PWA Formulation (i-PWA-QR?)

Space of \(x_1\)

x_1

\dots

Space of \(x_T\)

x_T

At every iteration, linearize the Lagrangian dynamics and enforce complementarity constraints with binary variables.
Update state, linearize, and repeat until convergence.

Space of \(x_0\)

x_0

:current time step.

:next time step.

Linearization reduces the number of pieces.
For systems with a handful of pieces, and using approximate solvers such as ADMM, the optimal control problem and be solved faster.

The controller can run at up to 240Hz for this 3-piece PWA system:

But slows down to 16Hz for a more complex system:

What does quasi-static mean?

Quasi-static \(\Longleftrightarrow \Sigma F = 0\)

But why is it a good idea?

Achieves stable integration with much larger time steps. (0.001s --> 0.4s)
- Ignores transient effects such as damping.
- Considers only transitions between equilibriums.
Smaller state space (\([q, v]\) vs. only \(q\)).

\mathbf{M}\ddot{q} + \mathbf{C}(q, \dot{q}) \dot{q} = \tau

0 = \tau

Second-order

mass matrix

Quasi-static

Coriolis Force

Torque (contact + actuation)

h = 0.001

h = 0.4

Quasi-static dynamical systems: what it was.

\( x_{+} = f(x, u)\)

\(x \coloneqq q \coloneqq [q^\mathrm{u}, q^\mathrm{a}]\): system configuration.
- \(q^\mathrm{a}\): actuated, imepdance-controlled robots
- \(q^\mathrm{u}\): un-actuated objects.
\( u \): robot velocities.

Zhou, Jiaji, et al. "A convex polynomial model for planar sliding mechanics: theory, application, and experimental validation." The International Journal of Robotics Research 37.2-3 (2018): 249-265.
Mason, Matthew T. "Mechanics and planning of manipulator pushing operations." The International Journal of Robotics Research 5.3 (1986): 53-71.
Hogan, François Robert, and Alberto Rodriguez. "Feedback control of the pusher-slider system: A story of hybrid and underactuated contact dynamics." Algorithmic Foundations of Robotics XII. Springer, Cham, 2020. 800-815.

\begin{cases} \end{cases}

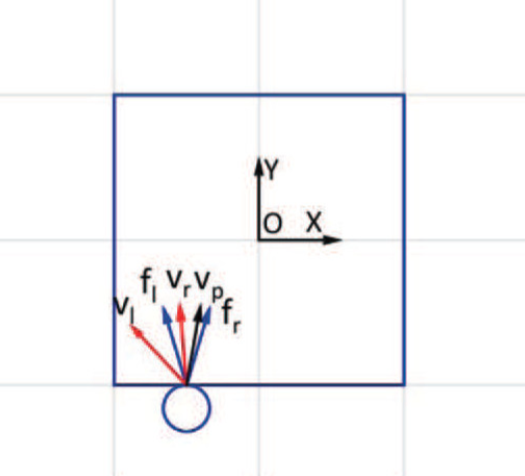
\(\mathrm{v}_p\): applied velocities by the manipulator end effector at the contact point. [1]

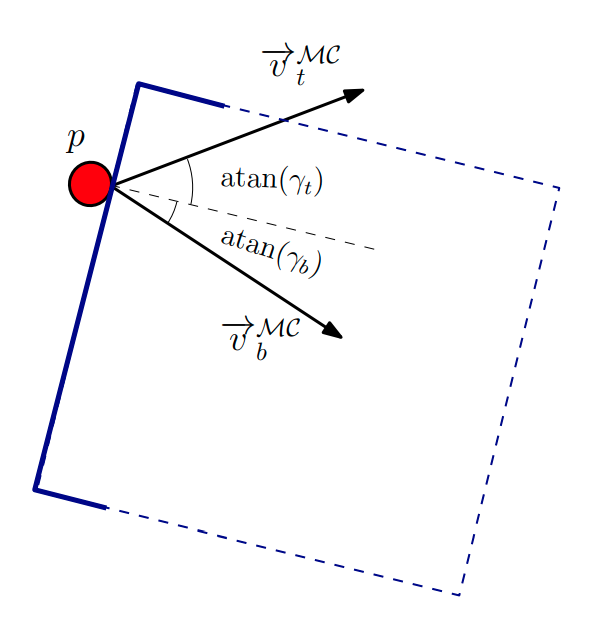
[3]

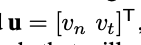
\(R_P\): "the ray of pushing". [2]

This is a good model for planar pushing:

Contact force cannot be uniquely determined from \(u\) when there is contact.
As a result, \(q_+\) cannot be determined from \(u\).
Defining \(u\) as velocity leads to ill-posed dynamical systems (invalid Bond Graphs).

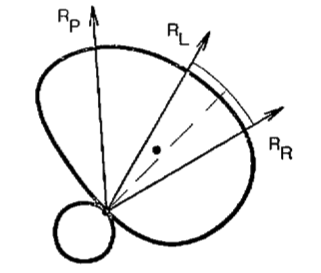
But what about grasping?

Quasi-static dynamical systems: how to fix it.

q^\mathrm{a}

m^\mathrm{a}

u

K

D

A Impedance-controlled 1D robot and an object.

m^\mathrm{u}

q^\mathrm{u}

Pang, Tao, and Russ Tedrake. "A convex quasistatic time-stepping scheme for rigid multibody systems with contact and friction." 2021 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2021.
Pang, Tao, and Russ Tedrake. "A robust time-stepping scheme for quasistatic rigid multibody systems." 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2018.

\( x_{+} = f(x, u)\)

\(x \coloneqq q \coloneqq [q^\mathrm{u}, q^\mathrm{a}]\): system configuration.
- \(q^\mathrm{a}\): actuated, imepdance-controlled robots
- \(q^\mathrm{u}\): un-actuated objects.
\( u \): ~~robot velocities.~~ position command to the impedance-controlled robots.

\begin{cases} \end{cases}

Contact force and \(q_+\) can now be uniquely* determined from \(u\), even for grasping.

Force-acceleration vs. Impulse-Momentum

q^\mathrm{a}

m^a \ddot{q}^\mathrm{a} + D \dot{q}^\mathrm{a} + K(q^\mathrm{a} - u) = 0

m^\mathrm{a}

u

``\Sigma F = ma"

Force-acceleration

K

D

Stewart, David E. "Rigid-body dynamics with friction and impact." SIAM review 42.1 (2000): 3-39.

``h\Sigma F = m\Delta v"

m^\mathrm{a} (\delta v) + hD v^\mathrm{a} + hK(q^\mathrm{a} + \delta q^\mathrm{a} - u) = 0

Impulse-momentum

0

\underset{\delta q^\mathrm{a}}{\min} \; \frac{1}{2} hK (q^\mathrm{a} + \delta q^\mathrm{a} - u)^2

is the optimality condition of

But impacts can lead to infinite forces (e.g. Painleve's Paradox) [1].

Time step

Quasi-static Dynamics with Contacts

hK(q^\mathrm{a} + \delta q^\mathrm{a} - u) = 0

\Leftrightarrow

\begin{cases} hK(q^\mathrm{a} + \delta q^\mathrm{a} - u) = -\lambda \\ 0 = \lambda \\ \underbrace{q^\mathrm{u} + \delta q^\mathrm{u} - q^\mathrm{a} - \delta q^\mathrm{a}}_{\phi (q + \delta q)} \geq 0 \\ \lambda \geq 0 \\ \phi (q + \delta q) \lambda = 0 \end{cases}

\begin{aligned} \underset{\delta q^\mathrm{a}, \delta q^\mathrm{u}}{\min} \; &\frac{1}{2} hK (q^\mathrm{a} + \delta q^\mathrm{a} - u)^2 \; \text{s.t.} \\ &\phi (q + \delta q)\geq 0 \end{aligned}

KKT

\Leftrightarrow

KKT

q^\mathrm{a}

u

K

\underset{\delta q^\mathrm{a}}{\min} \; \frac{1}{2} hK (q + \delta q^\mathrm{a} - u)^2

q^\mathrm{a}

u

K

m^\mathrm{u}

q^\mathrm{u}

\lambda

\phi({q})

: signed distance function.

Robot

Quasi-dynamic: Quasi-static with Regularization

q^\mathrm{a}

u

K

m^\mathrm{u}

q^\mathrm{u}

\lambda

\begin{aligned} \underset{\delta q^\mathrm{a}, \delta q^\mathrm{u}}{\min} \; &\frac{1}{2} hK (q + \delta q^\mathrm{a} - u)^2, \; \text{s.t.} \\ &\phi (q + \delta q)\geq 0 \end{aligned}

Quasi-static

The quadratic cost is semi-definite.
The object \(m^\mathrm{u}\) can be anywhere on the right of the robot, similar to having a null space.

Robot

\underset{x}{\min} \|Ax - b\|^2

\underset{x}{\min} \|Ax - b\|^2 + \epsilon \|x\|^2

Regularized least squares

Regularized Quasi-static

\begin{aligned} \underset{\delta q^\mathrm{a}, \delta q^\mathrm{u}}{\min} \; &\frac{1}{2} hK (q^\mathrm{a} + \delta q^\mathrm{a} - u)^2 + \frac{1}{2} \epsilon (\delta q^\mathrm{u})^2, \; \text{s.t.} \\ &\phi (q + \delta q)\geq 0 \end{aligned}

The quadratic cost is now definite.
"Among all possible object motions, give me the one that moves the least."
Picking \(\epsilon = m^\mathrm{u} / h\) gives Mason's definition of quasi-dynamic dynamics.

What about friction?

\begin{aligned} \underset{\delta q}{\min} \; &\frac{1}{2} {\underbrace{ \begin{bmatrix} \delta q^\mathrm{u} \\ \delta q^\mathrm{a} \end{bmatrix}}_{\delta q}}^\intercal \underbrace{ \begin{bmatrix} \mathbf{M}_\mathrm{u} / h & 0 \\ 0 & h \mathbf{K}_\mathrm{a} \end{bmatrix}}_{\mathbf{Q}} \underbrace{ \begin{bmatrix} \delta q^\mathrm{u} \\ \delta q^\mathrm{a} \end{bmatrix}}_{\delta q} + {\underbrace{ h \begin{bmatrix} - \tau^\mathrm{u} \\ - \mathbf{K}_\mathrm{a} (u - q^\mathrm{a}) - \tau^\mathrm{a} \end{bmatrix}}_{b}}^\intercal \underbrace{ \begin{bmatrix} \delta q^\mathrm{u} \\ \delta q^\mathrm{a} \end{bmatrix}}_{\delta q} \;\text{s.t.} \\ &\underbrace{\phi_i + \mathbf{J}_{\mathrm{n}_i}\delta q}_{\text{Linearized} \; \phi_i(q + \delta q)} \geq 0, \; \forall i \in \{1 \cdots n_{\mathrm{c}}\}. \end{aligned}

For a frictionless multi-body system with \(n_\mathrm{c}\) contacts, the dynamics can be solved as a Quadratic Program (QP):

\(\mathcal{K}^\star_i\) is the dual of the \(i\)-th friction cone.
Still convex! Convexity is achieved at the expense of "hydroplaning" between relatively-sliding objects.
But hydroplaning disappears as \(h \rightarrow 0\).

\begin{aligned} \underset{\delta q}{\min} \; &\frac{1}{2} {\delta q}^\intercal \mathbf{Q} \delta q + b^\intercal \delta q \;\text{s.t.} \\ & \begin{bmatrix} \phi_i + \mathbf{J}_{\mathrm{n}_i}\delta q \\ \mathbf{J}_{\mathrm{t}_i}\delta q \end{bmatrix} \succeq_{\mathcal{K}^\star_i} 0, \; \forall i \in \{1 \cdots n_{\mathrm{c}}\}. \end{aligned}

Anitescu [1] has a nice convex approximation of Coulomb friction constraints, allowing us to write down the dynamics as a Second-Order Cone Program (SOCP):

Tangential displacements

\begin{aligned} \underset{\delta q^\mathrm{a}, \delta q^\mathrm{u}}{\min} \; &\frac{1}{2} hK (q + \delta q^\mathrm{a} - u)^2 + \frac{1}{2} \frac{m^\mathrm{u}}{h} (\delta q^\mathrm{u})^2, \; \text{s.t.} \\ &\phi (q + \delta q)\geq 0 \end{aligned}

Dynamics of the 1D system with 1 contact

Anitescu, Mihai. "Optimization-based simulation of nonsmooth rigid multibody dynamics." Mathematical Programming 105.1 (2006): 113-143.

Differentiability

\begin{aligned} \delta q^\star \coloneqq \underset{\delta q}{\text{argmin}.} \; &\frac{1}{2} {\delta q}^\intercal \mathbf{Q} \delta q + b^\intercal \delta q \;\text{s.t.} \\ & \begin{bmatrix} \phi_i + \mathbf{J}_{\mathrm{n}_i}\delta q \\ \mathbf{J}_{\mathrm{t}_i}\delta q \end{bmatrix} \succeq_{\mathcal{K}^\star_i} 0, \; \forall i \in \{1 \cdots n_{\mathrm{c}}\}. \end{aligned}

Convex, Quasi-Dynamic, Differentiable Dynamics (an SOCP)

q_+ = f(q, u) = q + \delta q^\star(q, u)

\newcommand{\DfDx}[2]{\frac{\partial {#1}}{\partial {#2}}} \mathbf{A} \coloneqq \DfDx{f}{q} = \mathbf{I} + \DfDx{\delta q^\star}{q}, \; \mathbf{B} \coloneqq \DfDx{f}{u} = \DfDx{\delta q^\star}{u},

The KKT optimality condition of the dynamics SOCP defines equality constraints (including active contact constraints), from which the derivatives of \(\delta q^\star\) w.r.t. \((\mathbf{Q}, b, \phi_i, \mathbf{J}_{\mathrm{n}_i}, \mathbf{J}_{\mathrm{t}_i})\) can be computed using the Implicit Function Theorem (IFT).
\(\mathbf{A}, \mathbf{B}\) can then be computed using the gradients from IFT and the chain rule.
Standard practice for many differentiable simulators, even though many of them do not find the active constraints by solving convex programs.

Smoothing

The contact dynamics \(f(q, u) \in C^0\) has discontinuous gradients, which are bad for planning methods that use gradients.
Smoothing with "force at a distance" is a common method to alleviate this problem.

q^\mathrm{u}_+

u

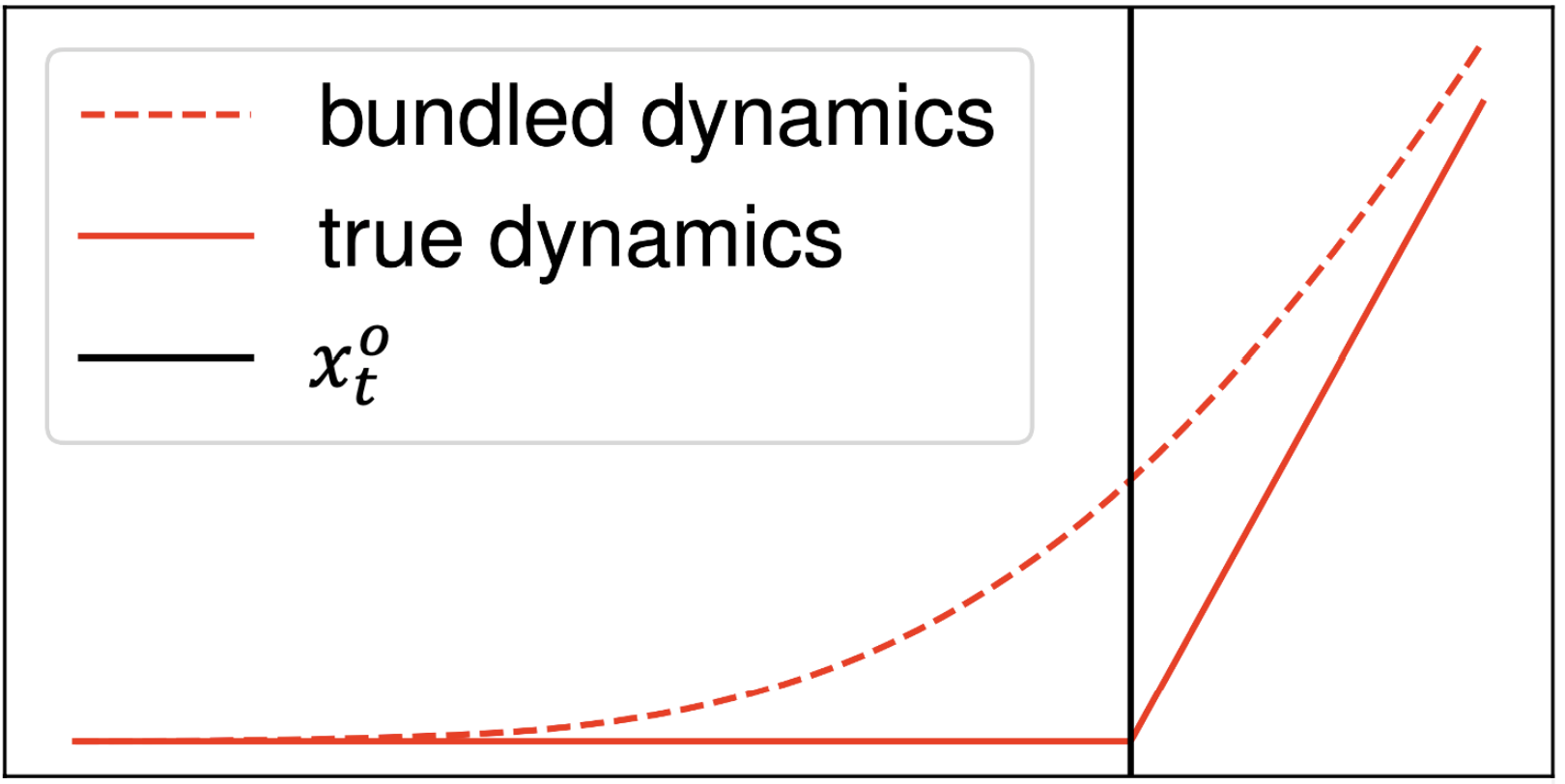
smoothed dynamics

original dynamics

\(q^\mathrm{u}\)

\begin{cases} hK(q^\mathrm{a} + \delta q^\mathrm{a} - u) = -\lambda \\ 0 = \lambda \\ \underbrace{q^\mathrm{u} + \delta q^\mathrm{u} - q^\mathrm{a} - \delta q^\mathrm{a}}_{\phi (q + \delta q)} \geq 0 \\ \lambda \geq 0 \\ \phi (q + \delta q) \lambda = 1 / \kappa \end{cases}

Smoothed Dynamics

Optimality Condition

\begin{aligned} \underset{\delta q^\mathrm{a}, \delta q^\mathrm{u}}{\min} \; &\frac{1}{2} hK (q + \delta q^\mathrm{a} - u)^2 + \frac{1}{2} \frac{m^\mathrm{u}}{h} (\delta q^\mathrm{u})^2 \\ &- \frac{1}{\kappa}\log{\phi(q + \delta q)} \end{aligned}

\Leftrightarrow

q^\mathrm{a}

u

K

m^\mathrm{u}

q^\mathrm{u}

\lambda

Robot

\begin{aligned} \underset{\delta q^\mathrm{a}, \delta q^\mathrm{u}}{\min} \; &\frac{1}{2} hK (q + \delta q^\mathrm{a} - u)^2 + \frac{1}{2} \frac{m^\mathrm{u}}{h} (\delta q^\mathrm{u})^2, \; \text{s.t.} \\ &\phi (q + \delta q)\geq 0 \end{aligned}

\begin{cases} hK(q^\mathrm{a} + \delta q^\mathrm{a} - u) = -\lambda \\ 0 = \lambda \\ \underbrace{q^\mathrm{u} + \delta q^\mathrm{u} - q^\mathrm{a} - \delta q^\mathrm{a}}_{\phi (q + \delta q)} \geq 0 \\ \lambda \geq 0 \\ \phi (q + \delta q) \lambda = 0 \end{cases}

\Leftrightarrow

KKT

Original Dynamics

Smoothing, the general case.

\begin{aligned} \underset{\delta q}{\text{min}.} \; &\frac{1}{2} {\delta q}^\intercal \mathbf{Q} \delta q + b^\intercal \delta q \;\text{s.t.} \\ & \begin{bmatrix} \phi_i + \mathbf{J}_{\mathrm{n}_i}\delta q \\ \mathbf{J}_{\mathrm{t}_i}\delta q \end{bmatrix} \succeq_{\mathcal{K}^\star_i} 0, \; \forall i \in \{1 \cdots n_{\mathrm{c}}\}. \end{aligned}

\underset{\delta q}{\text{min}.} \; \frac{1}{2} {\delta q}^\intercal \mathbf{Q} \delta q + b^\intercal \delta q - \frac{1}{\kappa} \sum_{i=1}^{n_\mathrm{c}} \log \left[ \frac{(\phi_i + \mathbf{J}_{\mathrm{n}_i}\delta q)^2}{\mu_i^2} - (\mathbf{J}_{\mathrm{t}_i}\delta q)^\intercal (\mathbf{J}_{\mathrm{t}_i}\delta q) \right]

Put constraints in a generalized log for \(\mathcal{\kappa}_i^\star\)

\Rightarrow

An unconstrained convex program.
Can be solved with Newton's method.
Also differentiable.

Convex, Quasi-Dynamic, Differentiable Dynamics (an SOCP)

Notation:

q_+ = f(q, u)

Original dynamics

q_+ = f_\rho(q, u)

Smoothed dynamics

What does quasi-dynamic mean?

Quasi-static \(\Longleftrightarrow \Sigma F = 0\)
Quasi-dynamic:
"Quasi-dynamic analysis is intermediate between quasi-static and dynamic. Suppose that a manipulation task involves occasional brief periods when there is no quasistatic balance. The task is then governed by Newton's laws. But in some instances, these periods are so brief that the accelerations do not integrate to significant velocities. Momentum and kinetic energy are negligible. Restitution in impact is negligible. It is as if a viscous ether is constantly damping all velocities and sucking the kinetic energy out of all moving bodies. We can analyze such a system by assuming it is at rest, calculating the total forces and body accelerations, then moving each body some short distance in the corresponding direction." -- Matt Mason <Dynamics of Robotic Manipulation>

But why is it a good idea?
- Benefits of quasi-static dynamics for planning:
  - Smaller state space (\([q, v]\) vs. only \(q\)).
  - Larger time steps.
- Quasi-dynamic is quasi-static with regularization.

\mathbf{M}\ddot{q} + \mathbf{C}(q, \dot{q}) \dot{q} = \tau

0 = \tau

Second-order

mass matrix

Quasi-static

Coriolis Force

Torque (contact + actuation)

\mathbf{M}\ddot{q} = \tau

Quasi-dynamic

Gradients of the smoothed dynamics enable trajectory optimization for dexterous hands

Task: Turning the ball by 30 degrees.

What about 180 degrees?

RRT is good at escaping local minima, but...

Kino-dynamic RRT needs a good distance metric! Think about the bycicle.
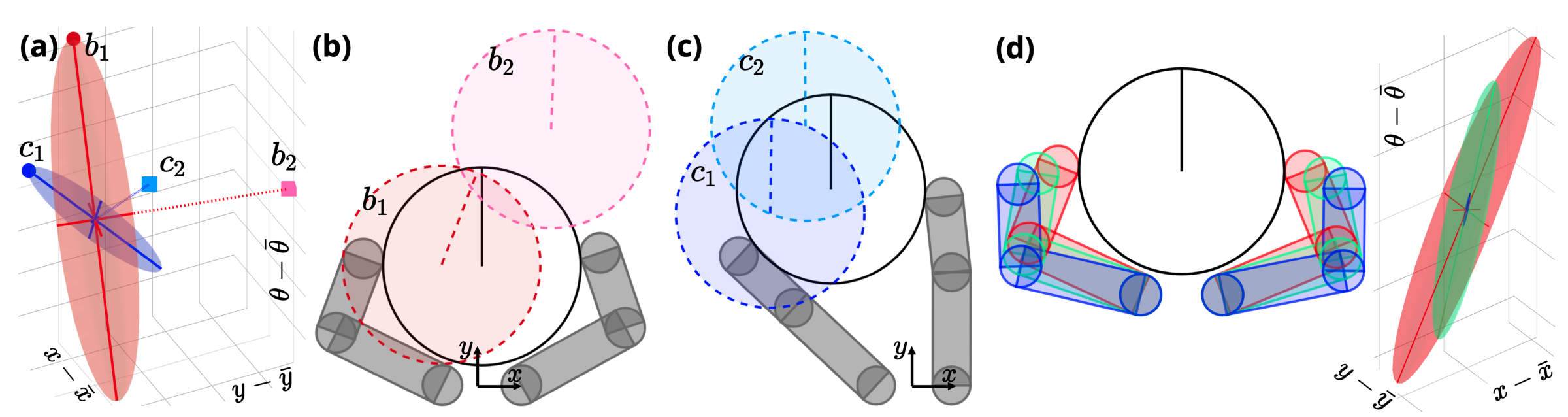
A good metric from a queried state \(q\) to a nominal state \(\bar{q}\) can be derived based on the smoothed linearization at \(\bar{q}\):

q_+ = \mu_\rho = f_\rho(x, u),

\newcommand{\DfDx}[2]{\frac{\partial {#1}}{\partial {#2}}} \mathbf{A}_\rho(q, u) \coloneqq \DfDx{f_\rho}{q}\big|_{q,u}, \\ \mathbf{B}_\rho(q, u) \coloneqq \DfDx{f_\rho}{u}\big|_{q,u}.

\begin{aligned} d^\mathrm{u}_{\rho, \gamma}(q; \bar{q}) &\coloneqq \frac{1}{2} (q^\mathrm{u} - \mu^\mathrm{u}_\rho)^\intercal {\mathbf{\Sigma}_{\rho, \gamma}^{\mathrm{u}}}^{-1} (q^\mathrm{u} - \mu^\mathrm{u}_\rho) \\ \mathbf{\Sigma}_{\rho, \gamma}^{\mathrm{u}} &\coloneqq \mathbf{B}_\rho^\mathrm{u} (\bar{q}, \bar{q}^\mathrm{a}) \mathbf{B}_\rho^\mathrm{u}(\bar{q}, \bar{q}^\mathrm{a})^\intercal + \gamma \mathbf I \\ \mu_\rho^\mathrm{u} &\coloneqq f_\rho^\mathrm{u}(\bar{q}, \bar{q}^\mathrm{a}) \end{aligned}

Regularization. \(\gamma\) is small.

\(\varepsilon \) sub-level set

No regularization

\mathcal{R}_{\rho, \varepsilon}^\mathrm{u} (\bar{q})\coloneqq \left\{\mathbf{B}_\rho^\mathrm{u}(\bar{q},\bar{q}^{\mathrm{a}}) \delta u + f_\rho^\mathrm{u}(\bar{q},\bar{q}^\mathrm{a})\; | \; \|\delta u\|\leq \varepsilon\right\}

Smoothed Contact Dynamics

\(d^\mathrm{u}_{\rho, \gamma}(q; \bar{q})\) is large (dominated by regularization) when

un-actauted(objects)

Smoothed.

Regularized.

q^\mathrm{u} - \mu^\mathrm{u}_\rho \notin \mathbf{Range}(\mathbf{B}^\mathrm{u}_\rho)

RRT through contact

Motivated by the need of a non-degenerate distance metric, two modifications to the vanilla RRT are made:

Connect: the nearest node on the tree to a sample \(q\) is computed using \( d^\mathrm{u}_{\rho, \gamma}(q; \bar{q}) \)
Contact sampling: with a non-zero probability, robot configuration is reset to one that has a good distance metric, which typically corresponds to grasps.

These modifications, together with smoothing, are essential for efficient state space exploration:

Distance Metric

\begin{aligned} d^\mathrm{u}_{\rho, \gamma}(q; \bar{q}) &\coloneqq \frac{1}{2} (q^\mathrm{u} - \mu^\mathrm{u}_\rho)^\intercal {\mathbf{\Sigma}_{\rho, \gamma}^{\mathrm{u}}}^{-1} (q^\mathrm{u} - \mu^\mathrm{u}_\rho) \\ \mathbf{\Sigma}_{\rho, \gamma}^{\mathrm{u}} &\coloneqq \mathbf{B}_\rho^\mathrm{u} (\bar{q}, \bar{q}^\mathrm{a}) \mathbf{B}_\rho^\mathrm{u}(\bar{q}, \bar{q}^\mathrm{a})^\intercal + \gamma \mathbf I \\ \mu_\rho^\mathrm{u} &\coloneqq f_\rho^\mathrm{u}(\bar{q}, \bar{q}^\mathrm{a}) \end{aligned}

RRT tree fro a simple system with contacts

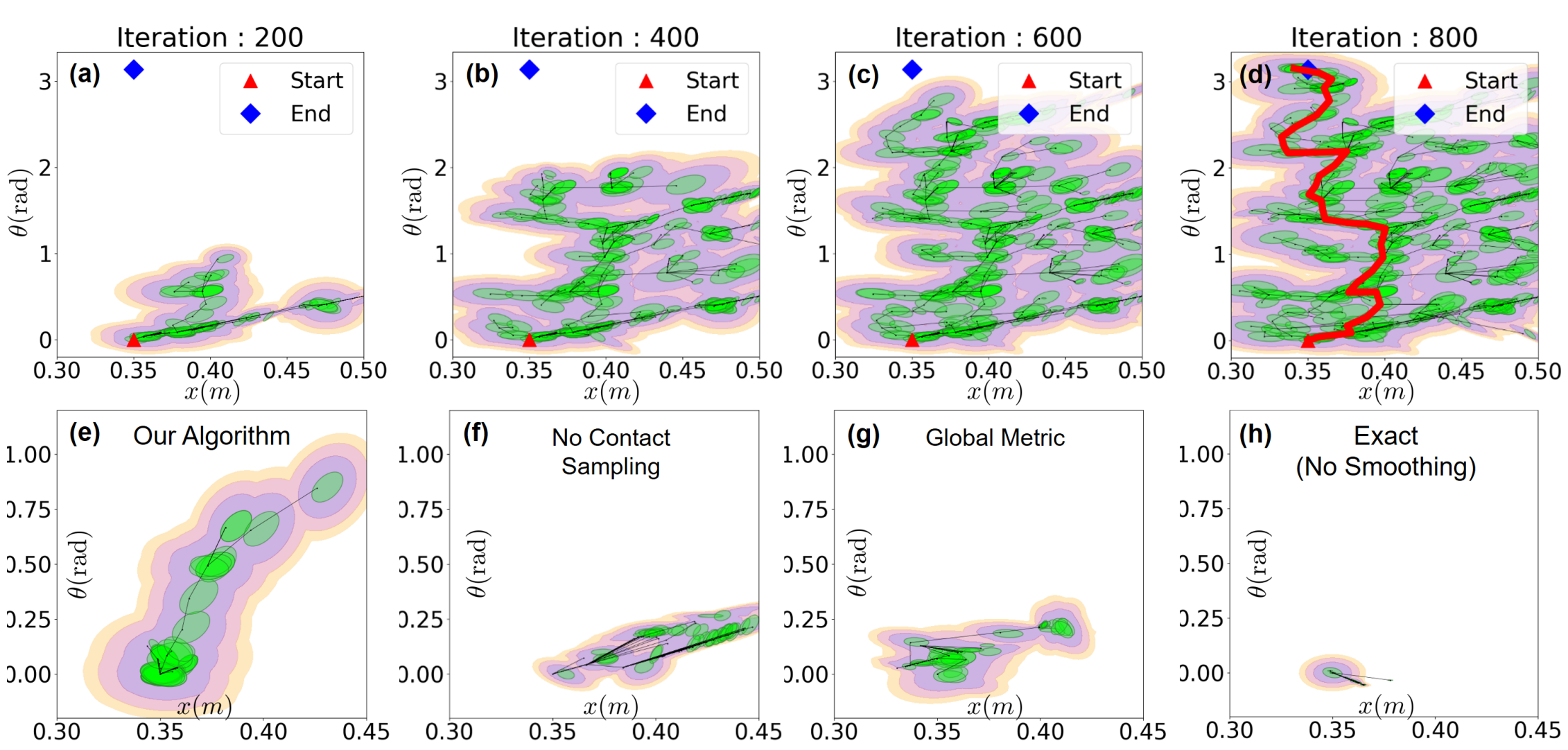
Ablation study: what trees look like after growing a fixed number of nodes.

The modified RRT works well for several systems!

Planning wall-clock time (seconds)

Smoothing by sampling

Smoothing directly

Stabilizing contact-rich plans

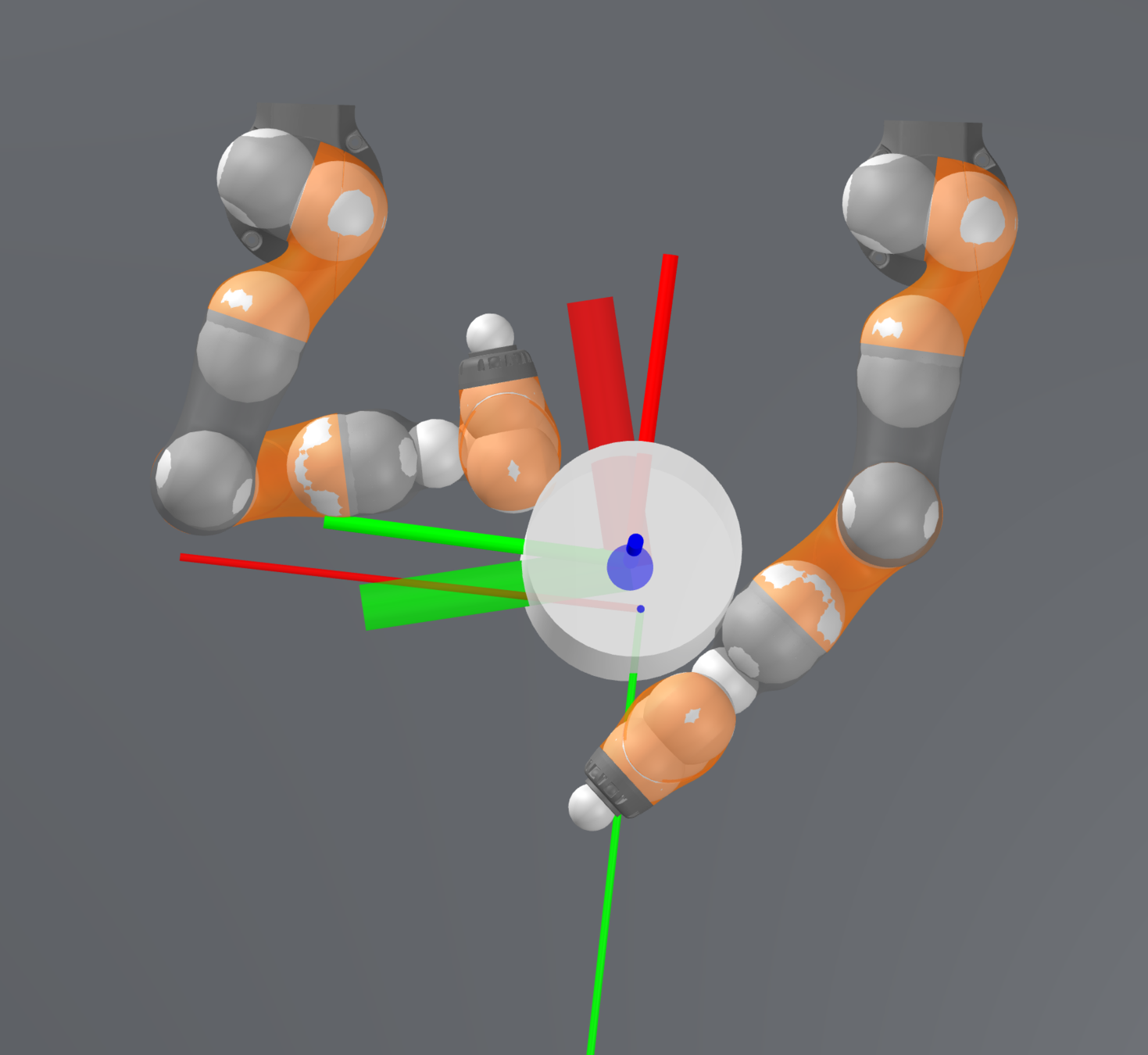
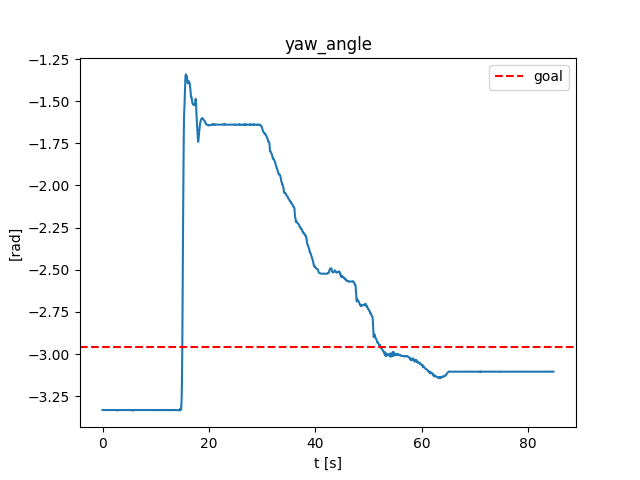
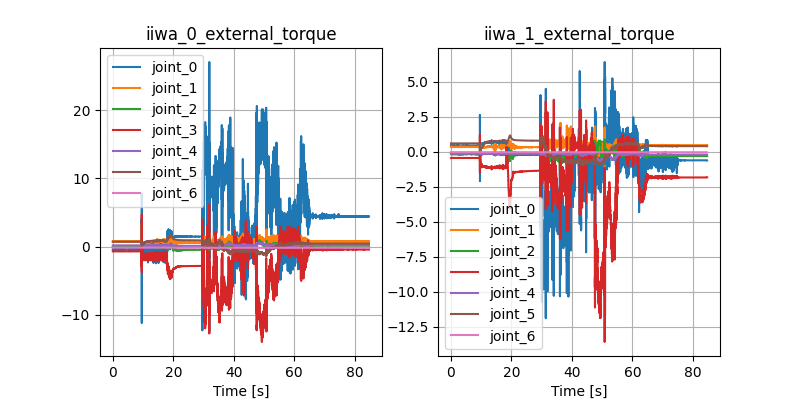
Open-loop

Closed-loop

Goal

Start

Final

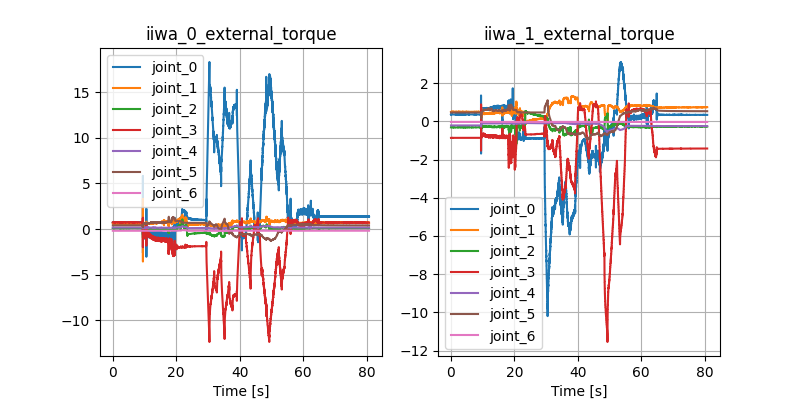
Stabilizing contact-rich plans

Open-loop hardware

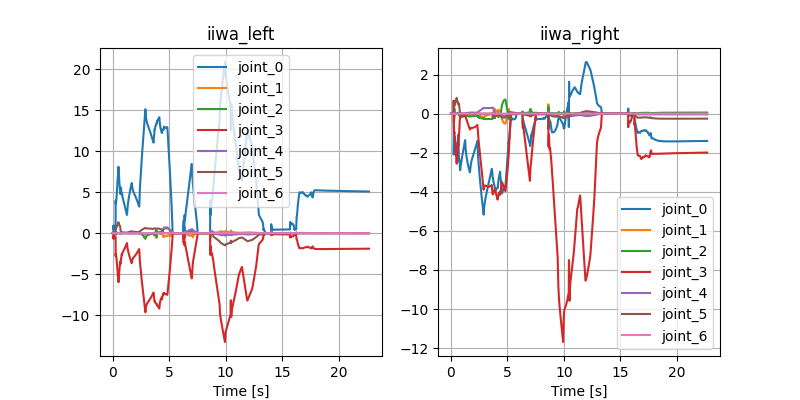
Open-loop Drake

Controller

Simple (and probably wrong) controller:

\begin{aligned} \underset{q^\mathrm{u}_+, u}{\min} &\|q_+^\mathrm{u} - q_+^\mathrm{u, ref}\|_\mathbf{Q} + \|u - u^\mathrm{ref} \|_\mathbf{R}, \text{s.t.}\\ & q^\mathrm{u}_+ = \mathbf{A}_\rho^\mathrm{u} q^\mathrm{u} + \mathbf{B}_\rho^\mathrm{u} u \end{aligned}

Smooth linearization

Consider modes?
Tracking joint torque?

Before my PhD defense in December 2022...

Stabilize this with MPC.
- Already done in Drake.
Potential problems:
- Robustness.
  - Shape variation.
  - Coefficient of friction.
  - etc.
Imperfect actuators.
- Poor tracking.
- Hysteresis.

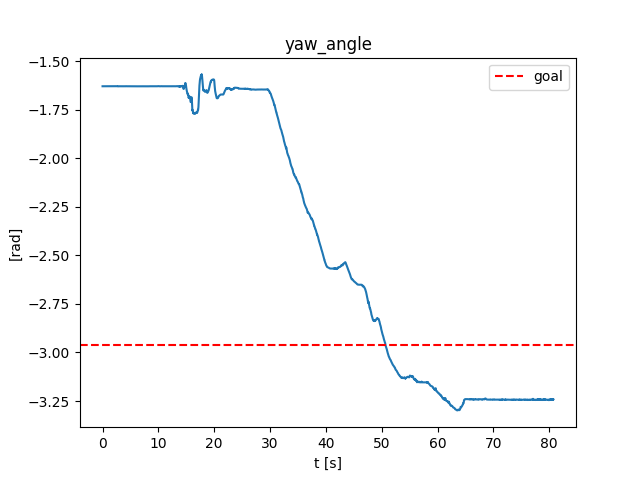
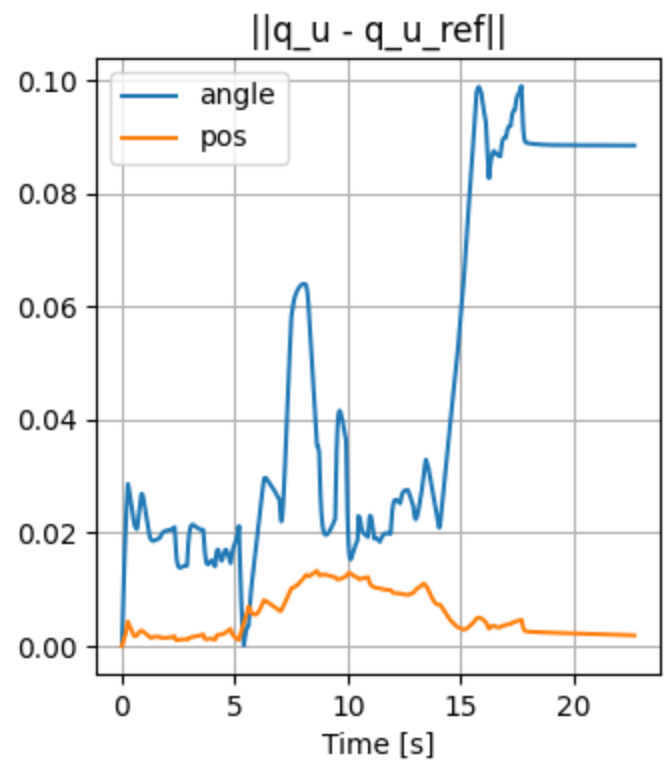
Turning the ball by 30 degrees: open-loop

Simulated in Drake with the same SDF as the quasi-dynamic model used for planning.

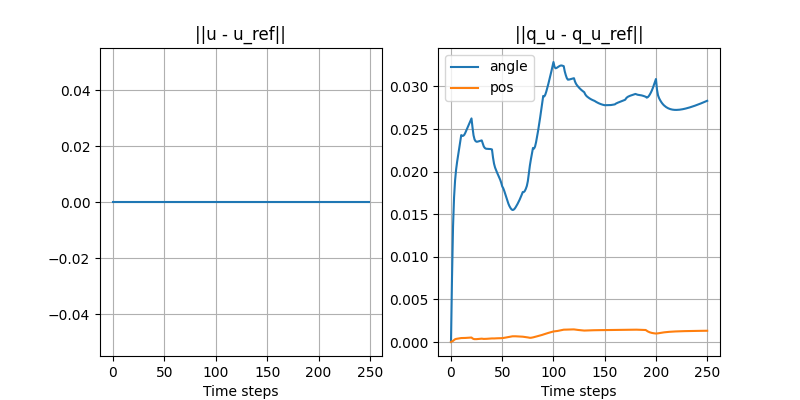
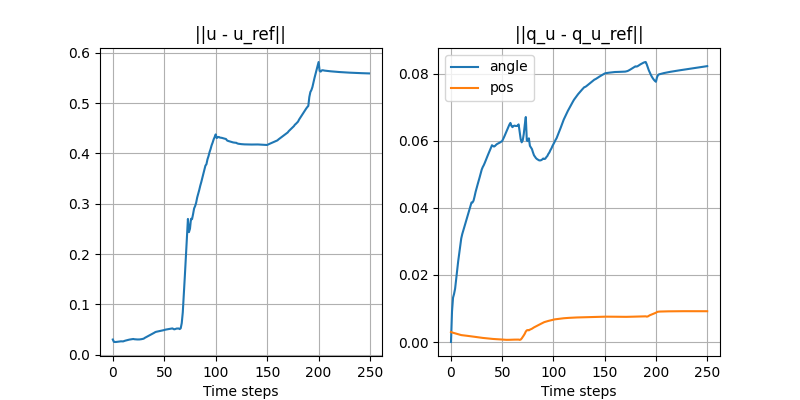
Turning the ball by 30 degrees: open-loop with disturbance

Initial position of the ball is off by 3mm.

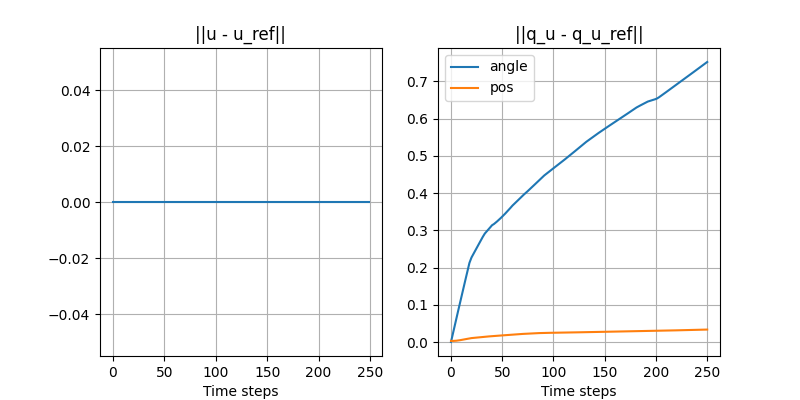
Turning the ball by 30 degrees: closed-loop with disturbance

Initial position of the ball is off by 3mm.
Simple controller:

\begin{aligned} \underset{q^\mathrm{u}_+, u}{\min} &\|q_+^\mathrm{u} - q_+^\mathrm{u, ref}\|_\mathbf{Q} + \|u - u^\mathrm{ref} \|_\mathbf{R}, \text{s.t.}\\ & q^\mathrm{u}_+ = \mathbf{A}_\rho^\mathrm{u} q^\mathrm{u} + \mathbf{B}_\rho^\mathrm{u} u \end{aligned}

Smooth linearization

Planning and Control for Contact-rich Manipulation

Why contact-rich?

Why contact-rich?

Why contact-rich?

Why don't we do RL (reinforcement learning)?

2018

Model-based Planning through Contact: a Quick Review

2014

2017

2021

2022: Our Method

Global PWA Formulation

Local PWA Formulation (i-PWA-QR?)

Overview: why did our contact-rich planner work?

What does quasi-static mean?

Quasi-static dynamical systems: what it was.

\( x_{+} = f(x, u)\)

Quasi-static dynamical systems: how to fix it.

\( x_{+} = f(x, u)\)

Force-acceleration vs. Impulse-Momentum

Quasi-static Dynamics with Contacts

Quasi-dynamic: Quasi-static with Regularization

Quasi-static

Regularized Quasi-static

What about friction?

Dynamics of the 1D system with 1 contact

Differentiability

Convex, Quasi-Dynamic, Differentiable Dynamics (an SOCP)

Smoothing

Smoothed Dynamics

Original Dynamics

Smoothing, the general case.

Convex, Quasi-Dynamic, Differentiable Dynamics (an SOCP)

What does quasi-dynamic mean?

Gradients of the smoothed dynamics enable trajectory optimization for dexterous hands

RRT is good at escaping local minima, but...

Smoothed Contact Dynamics

RRT through contact

Distance Metric

The modified RRT works well for several systems!

Stabilizing contact-rich plans

Stabilizing contact-rich plans

Controller

Before my PhD defense in December 2022...

Turning the ball by 30 degrees: open-loop

Turning the ball by 30 degrees: open-loop with disturbance

Turning the ball by 30 degrees: closed-loop with disturbance