Spatial
Data Structures
Context
In the previous lecture, we looked at some of the issues involved in detecting collisions between the entities
(aka objects) in a dynamic simulation.
(aka objects) in a dynamic simulation.
In particular, we recognised that the detection task was essentially a geometry problem, and that we should perform the collision checks "one entity at a time", to ensure that
we'll always have a "safe place" to fall back to
(i.e. the entity's previous location).
we'll always have a "safe place" to fall back to
(i.e. the entity's previous location).
Scaling
However, what we didn't really talk about (much) was how
to work out which entities we should be checking against...
to work out which entities we should be checking against...
Theoretically, without any prior knowledge, every time we move something in a simulation, we'd technically have to collision-check it against every other entity in the system.
Perhaps you recognise what this implies? ...
O(N^2)
Oh no!
In Favour Of Grids
...actually, in one case, we did address the scaling problem.
If you put your terrain on a regular grid, then you don't
need to explicitly check against every triangle in it.
need to explicitly check against every triangle in it.
You can use the moving entity's co-ordinates to quickly compute which part of the grid it is "over" and use that knowledge to index directly into the height-map array.
With N moving objects, this is just an O(N) computation.
And O(N) is OK!
..But..
...If the entities themselves are "freely moving", then they
don't naturally align to such a grid, and we still have to perform a full O(N^2) set of checks between them.
don't naturally align to such a grid, and we still have to perform a full O(N^2) set of checks between them.
As the number of entities increases into the dozens and,
in particular, the hundreds (or, today, the thousands),
this starts to become really slow.
in particular, the hundreds (or, today, the thousands),
this starts to become really slow.
Yes, this happened on GTA too. ;-)
I Want A Grid!
If only the main dynamic entities were somehow organised
on a controlled grid, we could apply the same "fast lookup" trick to them as we do to a height-mapped terrain.
on a controlled grid, we could apply the same "fast lookup" trick to them as we do to a height-mapped terrain.
SO LET'S DO THAT THEN!
It doesn't happen entirely "for free",
but we can implement it...
but we can implement it...
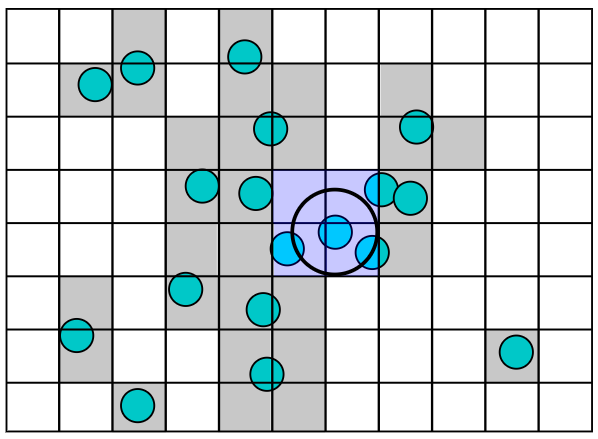
For Example
Here is a simple grid, with some objects on it...

So, Now What?
Well, now, when an object moves, we only need to perform the collision check against those entities which are in nearby cells of the grid.
Specifically, we compute the "collision footprint" of our moving entity, and identify the subset of the grid
which it overlaps with.
which it overlaps with.
Then we only need to perform "real" collision detection
against the (hopefully small) number of entities
in that little subset of the overall grid.
against the (hopefully small) number of entities
in that little subset of the overall grid.
Tracking
However, in order to make this work, we do have
to keep track of which grid cell (or, potentially, cells)
each entity overlaps with.
to keep track of which grid cell (or, potentially, cells)
each entity overlaps with.
The price you pay, then, is the need to recompute
these grid overlaps every time something moves.
these grid overlaps every time something moves.
You can no longer simply change an entity's
co-ordinates directly, whenever you feel like it...
co-ordinates directly, whenever you feel like it...
My Co-ords Are Private!
This constraint means that we can't just litter our code
with stuff like "someEntity.x = newPos"
with stuff like "someEntity.x = newPos"
...but we shouldn't really have been doing that anyway. ;-)
Each entity should be in charge of its own positional updates and, if so, it becomes easy to modify the relevant access functions so that they update the grid-tracking stuff too.
Who's In Charge Around Here?
We still need to manage the global state of this magic hypothetical grid of ours though. How should we do that?
Clue: Give it a "Manager".
Just as we have the entityManager to organise all the
update-and-render stuff, we can introduce something
similar to handle the grid (or whatever we use).
update-and-render stuff, we can introduce something
similar to handle the grid (or whatever we use).
We could call this the "spatialManager".
Code
With such a manager in place, our revised entity update
code will tend to look something like this:
code will tend to look something like this:
thing.prototype._init = function () {
// get a spatial "handle" for later
this._spatialID = spatialManager.getNewSpatialID();
};
thing.prototype.update = function (du) {
// take me out of the grid at my old place
spatialManager.unregister(this);
// move me, maybe
this._updatePosition(du);
// put me back in the grid at my new place
spatialManager.register(this);
};
thing.prototype.getPos = function () { /* spatialManager calls this */ }
thing.prototype.getSpatialID = ... /* and this */Multi-Cellular Entities
An entity at the edges / corners of the grid, can potentially
be in multiple cells simultaneously...
be in multiple cells simultaneously...
..Or..
If we limit the size of our objects, we can just anchor them
to whichever grid cell their centre-point is on...
to whichever grid cell their centre-point is on...
...They can still overlap into immediately neighbouring cells, of course, but we can handle this by simply extending the "footprint" that we use to determine which cells to check against by the "radius" of the biggest object.
Complexity
It seems reasonably clear that, by implementing such a grid, we can reduce the number of collision-checks that
we need to compute... but, by how much?
we need to compute... but, by how much?
Well, on average, we've just divided the original
number by however many cells are in the grid.
number by however many cells are in the grid.
So, we've gone from O(N^2) to... O(N^2 / numCells)
...which, technically, is still O(N^2) :-(
...albeit a better N^2.
Still Not Ideal
The problem is, that if we double the number of objects in our simulation, we'll still double the average number of objects
per cell, and have twice as many objects to worry about.
per cell, and have twice as many objects to worry about.
In other words, we'll have four times the work to do. :-(
...However, if we double (or quadruple) the number of
grid cells, we could compensate for this either partially
(or wholly).
grid cells, we could compensate for this either partially
(or wholly).
But knowing how many cells is "optimal" isn't automatic...
Quadtrees
...But, if we're clever, we can implement an "adaptive" grid,
which automatically reduces the size of its cells
based on how full they are!
which automatically reduces the size of its cells
based on how full they are!
This scales really well, and does so automatically, at runtime!
...so it's a good choice for general purpose "engines".
This is just the 2D generalisation of the Binary Tree
that you will already be familiar with.
that you will already be familiar with.
Subdivision
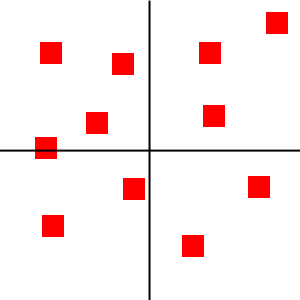
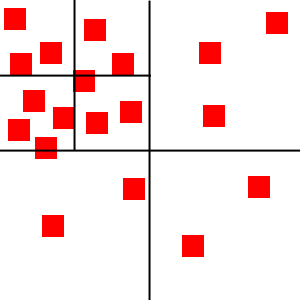
When the population of any cell gets too large,
we split it into four smaller cells.
we split it into four smaller cells.
More Subdivisions!

3D?
The 3 dimensional extension of the Quadtree is an
8-childed structure known, unsurprisingly, as an Octree.
8-childed structure known, unsurprisingly, as an Octree.

Fancy!
By using "fancy" adaptive data-structures such as Quadtrees, Octrees, kd-Trees, or BSP-Trees (as famously used by Quake), we can produce reasonably scalable collision solutions for
very large environments.
very large environments.
Here is a BIG SECRET:
Often, we can just get away with a Big Dumb Grid.
(That's what we used on APB, and it was actually faster, and simpler, than the alternative Octree implementation!)
Homework!
Modify last week's "Entities" exercise by adding a "spatialManager" which tracks the positions of the
Rocks and Bullets and Ships, and uses this info
to implement collisions between them.
Rocks and Bullets and Ships, and uses this info
to implement collisions between them.
When a Rock is hit by a Bullet, it should split into smaller "baby rocks" of half the size... until those become too small,
at which point we just ignore them.
at which point we just ignore them.
Just treat the collision environment as One Big Cell.
Yes, this is O(N^2), but N is very small here, so it's OK.
A Big Subject!
Like collision-detection, and much of the other stuff that
I'll be covering in the remaining weeks of this course,
"Spatial Data Structures" are, literally,
a subject in their own right.
I'll be covering in the remaining weeks of this course,
"Spatial Data Structures" are, literally,
a subject in their own right.
...an entire semester's worth, in fact!
Which we've just summarised in 40 mins.
Speed Learning!
When Collision Goes Wrong
...no, it's not another episode of: "When Things Fall Over,
Spill, Or Get Knocked Out Of Cupboards"
Spill, Or Get Knocked Out Of Cupboards"
Homework Hints
The Bullets are the "aggressors" in this game:
when they collide with things, they HURT THEM!
when they collide with things, they HURT THEM!
The Rocks themselves are pretty dumb and passive.
When a Ship collides with a Rock, or another Ship,
we could "kill" it... or we could just warp it away
(which is what we'll do, for convenience).
we could "kill" it... or we could just warp it away
(which is what we'll do, for convenience).
In a real system, we'd have a "matrix" defining which types of object collide with each other, and what effects they have...
Keep It Simple Stupid
...in our case, we can afford to be a bit simplistic here,
and just "hard code" the expected behaviour into
the various entity "update" methods.
and just "hard code" the expected behaviour into
the various entity "update" methods.
Good Luck!