These slides:

https://s.ntnu.no/irobot

F for fullscreen

SPACE to advance

ESC to zoom out

 

Slides progress downward,

then to next column

Single-View 3D Shape Completion

for Robotic Grasping of Objects

via Deep Neural Fields

A MsC by
Peder Bergebakken Sundt

Motivation

Motivation

?

Panda Emika 7-DoF robot arm

With

Intel Realsense 3D vision

Single-View 3D Shape Completion

for Robotic Grasping of Objects

via Deep Neural Fields

A MsC by
Peder Bergebakken Sundt

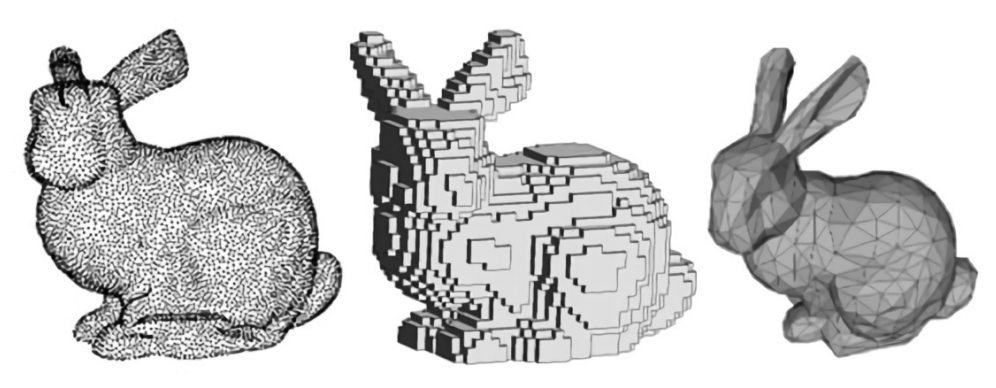
Affected by
point order,
no topology.

Scales poorly

Either limited

topologically or

self-intersecting

... all map poorly to neural networks!

Explicit 3D shape representations

Points

Voxels

Meshes

A new concept, first explored in 2019

"We have many names for the things we love:"

  • [Deep] Neural Fields
  • Coordinate-based Neural Networks
  • Implicit Representation Network

Park JJ, Florence P, Straub J, Newcombe R, Lovegrove S. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA: IEEE; 2019, p. 165–74. https://doi.org/10.1109/CVPR.2019.00025.

"We have many names for the things we love:"

  • [Deep] Neural Fields
  • Coordinate-based Neural Networks
  • Implicit Representation Network

Park JJ, Florence P, Straub J, Newcombe R, Lovegrove S. DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA: IEEE; 2019, p. 165–74. https://doi.org/10.1109/CVPR.2019.00025.

A new concept, first explored in 2019

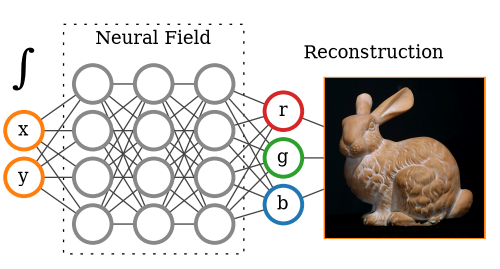
Query

coordinates

Value at

coordinate

An example:

2D RGB Field

\Phi _{\theta } \space :\space \mathbb{R} ^{2} \rightarrow \mathbb{R} ^{3}

Trained on (x,y,r,g,b) tuples

3D Implicit Neural Representations have
several benefits:

  • They represent shapes as continuous functions.
    • Continuous -> arbitrary reconstruction resolution
    • Perfect for partial data, enables single view shape completion
  • The network size not tied to the resolution of 3D models.
    • Networks only scale with shape complexity, not size!
  • Seamlessly allow for learning latent spaces of functions.
    • Enables shape completion drawing from learned priors.
f(\bold{x} )=y\space :\mathbb{R} ^3\rightarrow \mathbb{R}
f(\cdot )=0
\|\nabla _{\bold{x} } f\|_{2} =1

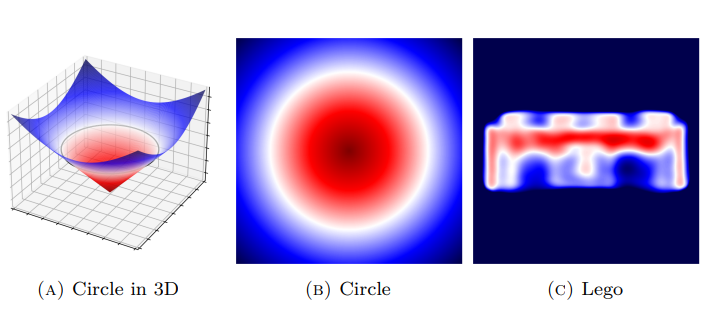
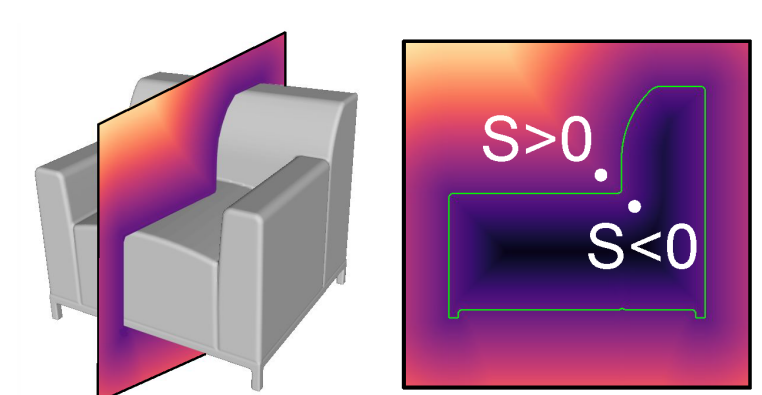
Signed Distance Functions (SDF)

Implicit Isosurface

Metric Constraint

Moving to 3D...

f(\bold{x} )=y\space :\mathbb{R} ^3\rightarrow \mathbb{R}

Signed Distance Functions (SDF)

\Phi_\theta(\bold{x} )=y\space :\mathbb{R} ^3\rightarrow \mathbb{R}

Signed Distance Functions (SDF)

Train it on (x, y) tuples

Signed Distance Functions (SDF)

Marching Cubes

+

\Phi_\theta(\bold{x} )=y\space :\mathbb{R} ^3\rightarrow \mathbb{R}

Train it on (x, y) tuples

3D models provided by

The YCB dataset

Training data

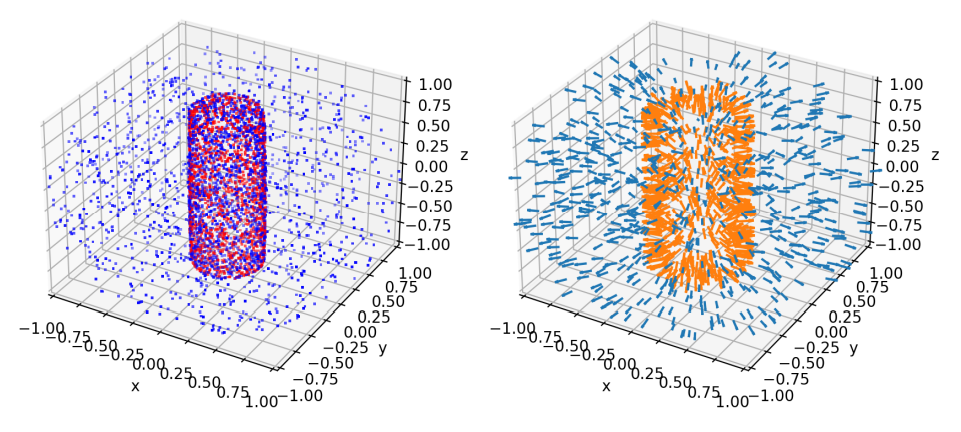
Signed Distances

Gradients

Positive SDF

Negative SDF

⬤

⬤

Free-space

Near-surface

⬤

⬤

Training data

Mesh

\Rightarrow
f(\bold x)
\nabla_{\bold x}f(\bold x)

Gradients

Positive SDF

Negative SDF

⬤

⬤

Free-space

Near-surface

⬤

⬤

\mathcal{L} (y,\hat{y} )=
|y-\hat{y} |
+\ \ \ (1 - \langle \nabla_{\bold x}y, \nabla_{\bold x}\hat y \rangle)

(Cosine similarity)

Mesh

Loss

Signed Distances

Requires us to compute
the derivative of the network itself

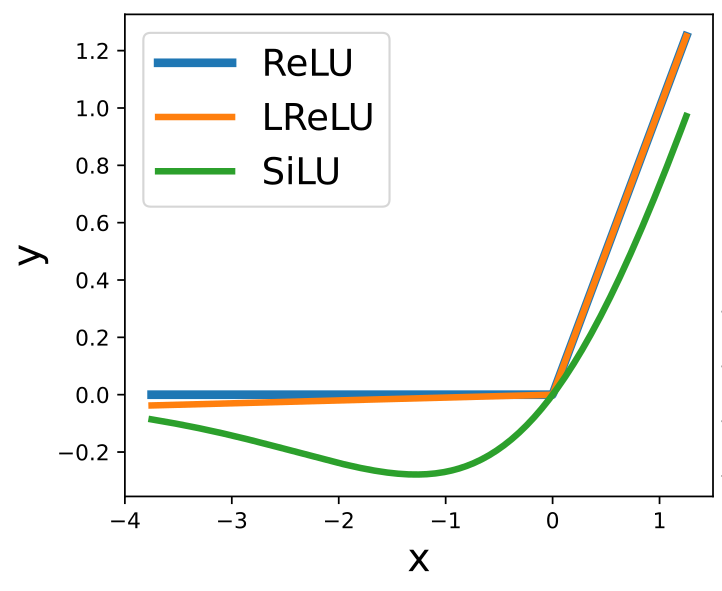
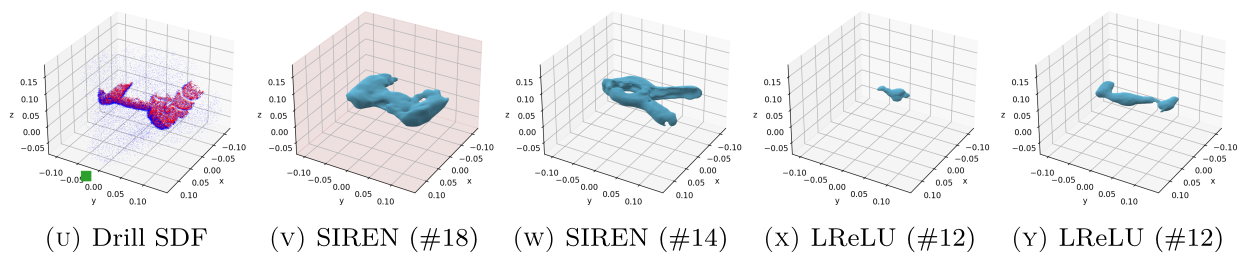
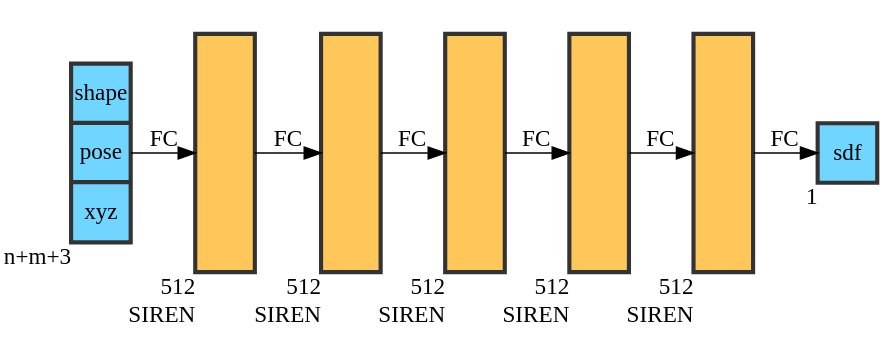
ReLU-based

Sinusoidal

\max (0, x)
\sin (x)
  • Piecewise linear
  • Second derivative is zero!

Activation Function

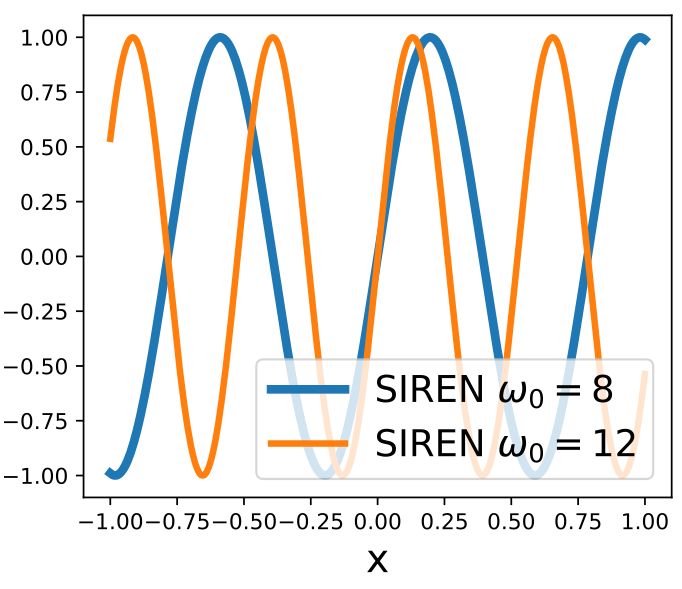
SIREN

\sin (\omega_0 x)
  • Piecewise linear
  • Second derivative is zero!
  • Can represent complex signals
  • The derivative of a SIREN
    is another SIREN!

Activation Function

ReLU-based

\max (0, x)

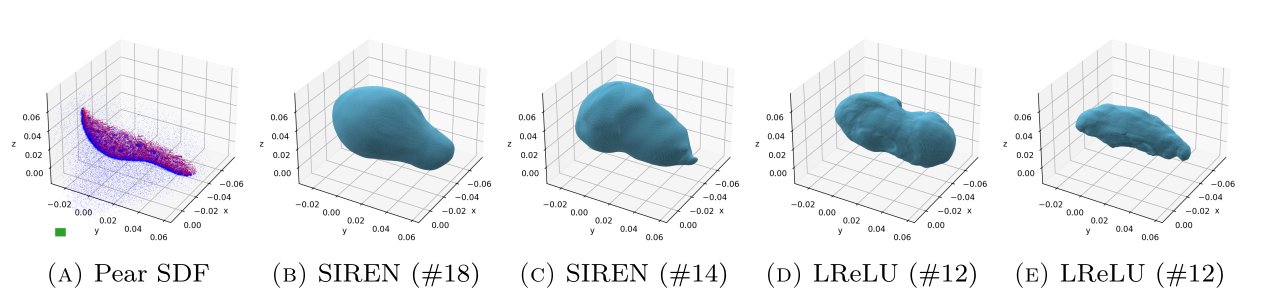
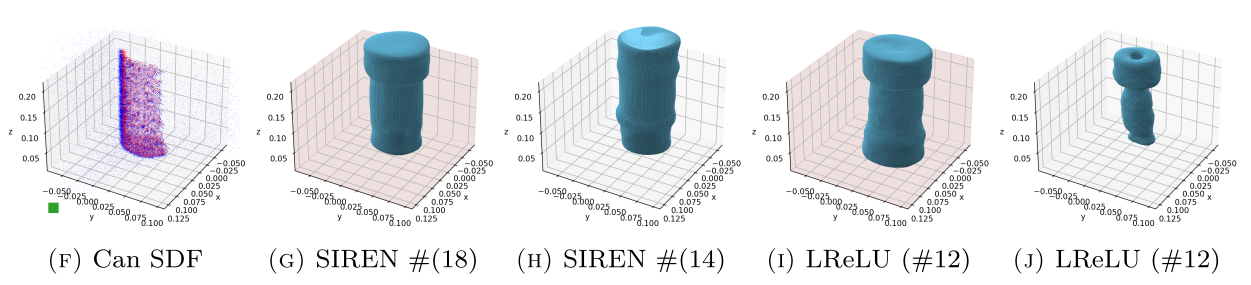
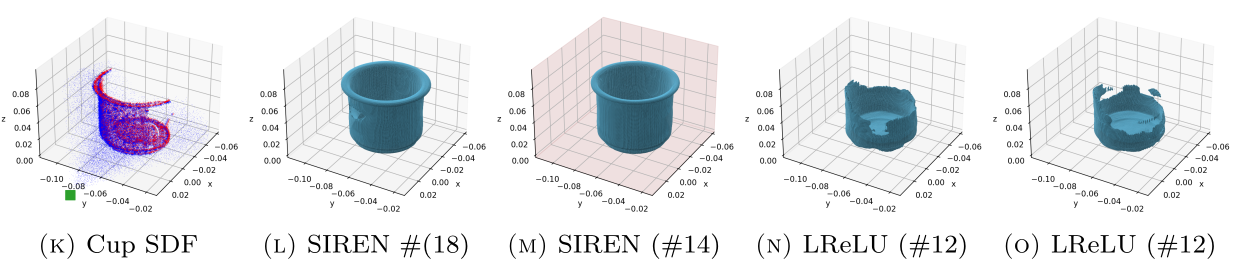
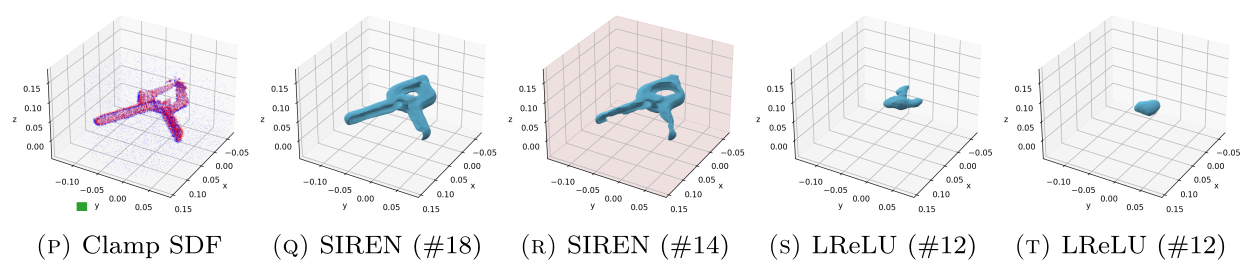
Ground-

Truth

ReLU

ReLU

w/gradients

SIREN

w/gradients

ReLU-based networks

SIREN networks

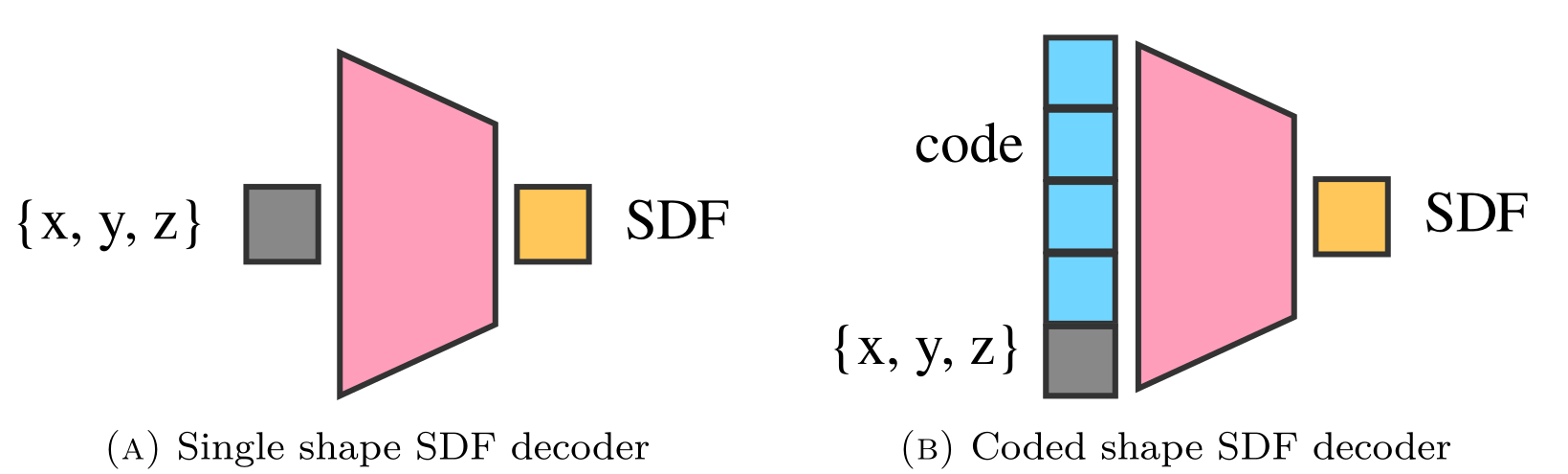
Learning a useful space of

prior shapes

Coded decoders

Embedding more than one shape

Learning latent spaces

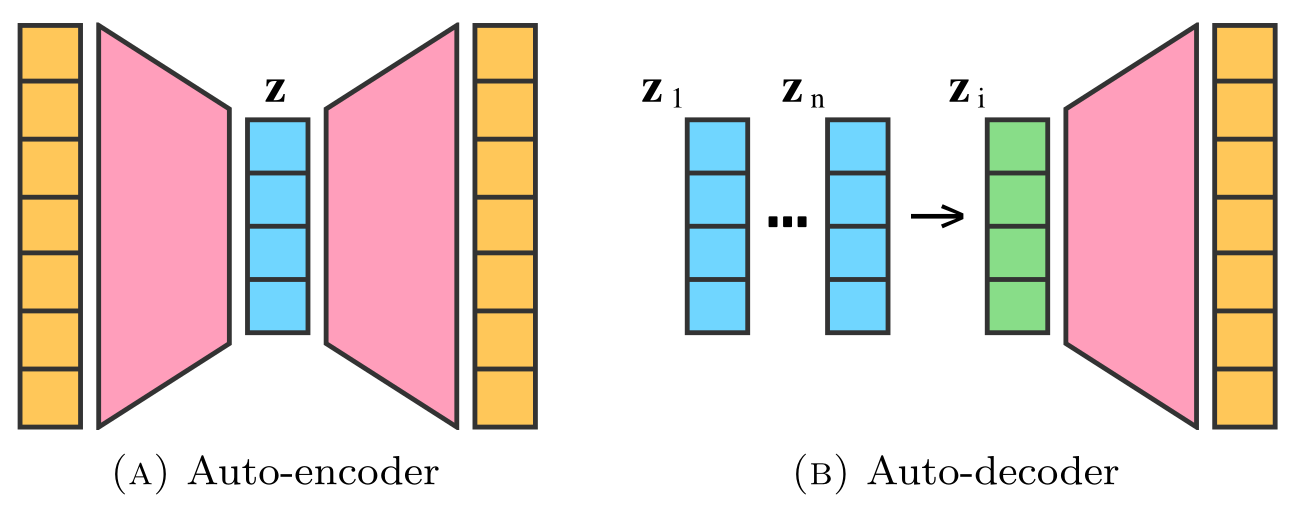
Auto-encoders map poorly

to learning implicit functions...

... and treat the latent vectors as learnable parameters!

-> Just skip the encoder!

Keep a database
of codes per object

\sum_y \mathcal{L}(y, \hat{y})

Add a regularizing cost to each latent code in the auto-decoder database:

+ \lambda\frac{1}{|\Omega |} \sum_{i\in \Omega }^{}{\|\bold{z} _{i} \|_2 }

Problem: Learned latent vectors drift apart!

Pulls each code (z) towards 0, and

incentivise a spherical distribution  

\Rightarrow

(Reconstruction loss)

(Latent code regularization)

and generalization. 

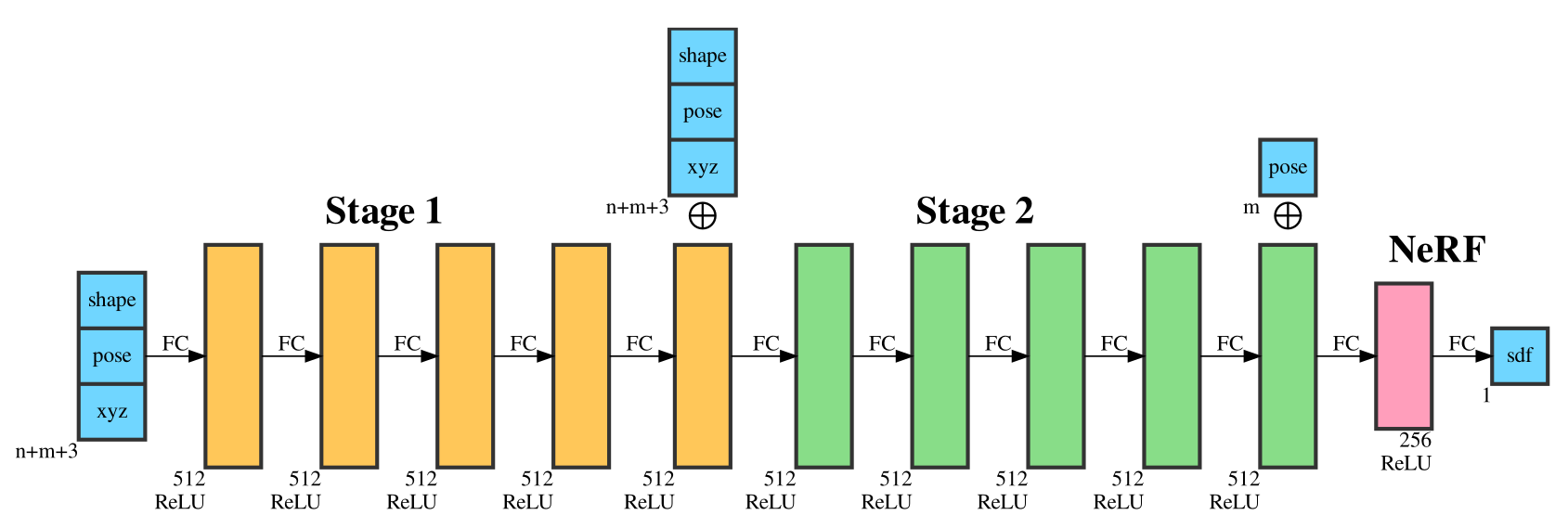
Pose?

\approx
\text{SDF}_i(\bold x)
\Phi_\theta(\bold x, \bold{z}_i)

We need:

  • Rotation (R)
  • Scale (s)
  • Translation (t)

Pose

\approx
s\cdot \text{SDF}_i (\bold{R} (s\cdot \bold{x} )+\bold{t} )
\Phi _{\theta } (\bold{x} ,\bold{R} ,s,\bold{t} , \bold{z}_i)

We need:

  • Rotation (R)
  • Scale (s)
  • Translation (t)

Then we train with random transformations,

and discover the pose via gradient decent at test time

Single-view data

We sample SDF points from two distributions:

  • Near-surface samples: For surface details
  • Ambient space samples: Improves generalization

 

The these two distributions
are balanced 90% / 10%

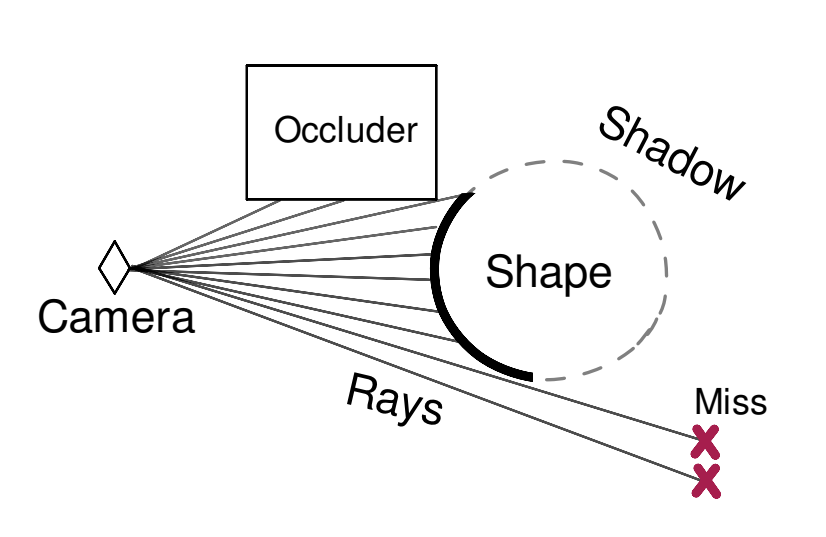
Single-view data

Hit

Miss

Camera

⬤

⬤

⬤

Positive

Negative

⬤

⬤

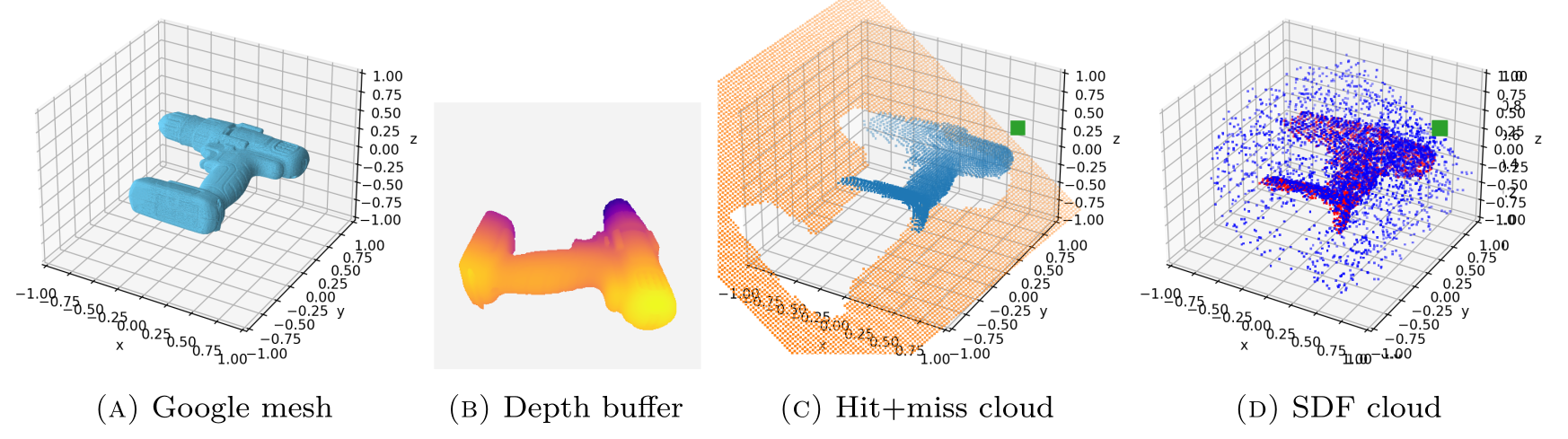
Sampling pipeline

Single-view data

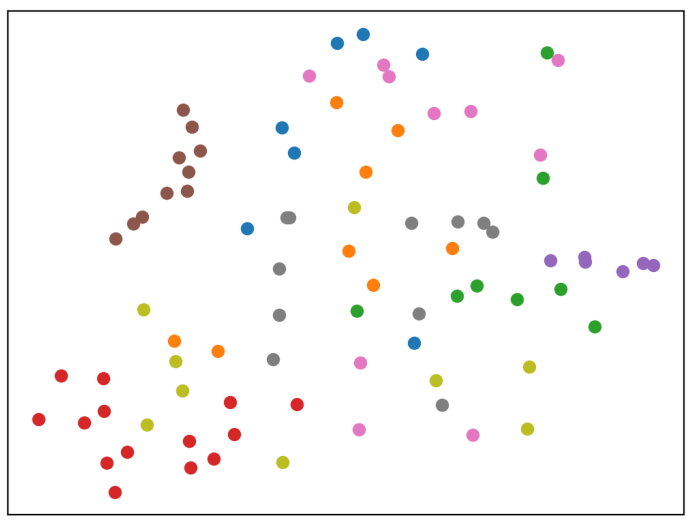
T-SNE of learned latent vectors

Shape completion:

  • Start near the mean class vector (classifier needed)
  • Further optimize the vector w.r.t. partial observation
    using gradient decent

(start)

(end)

A Search

BigBIRD Scanner

Real data?

\Rightarrow

!

From the YCB data- and object set

BigBIRD Scanner

Color

Depth

\Rightarrow

!

Positive SDF

Negative SDF

Unit sphere

Reconstruction

volume

⬤

⬤

⬤

⬤

Bounding box?

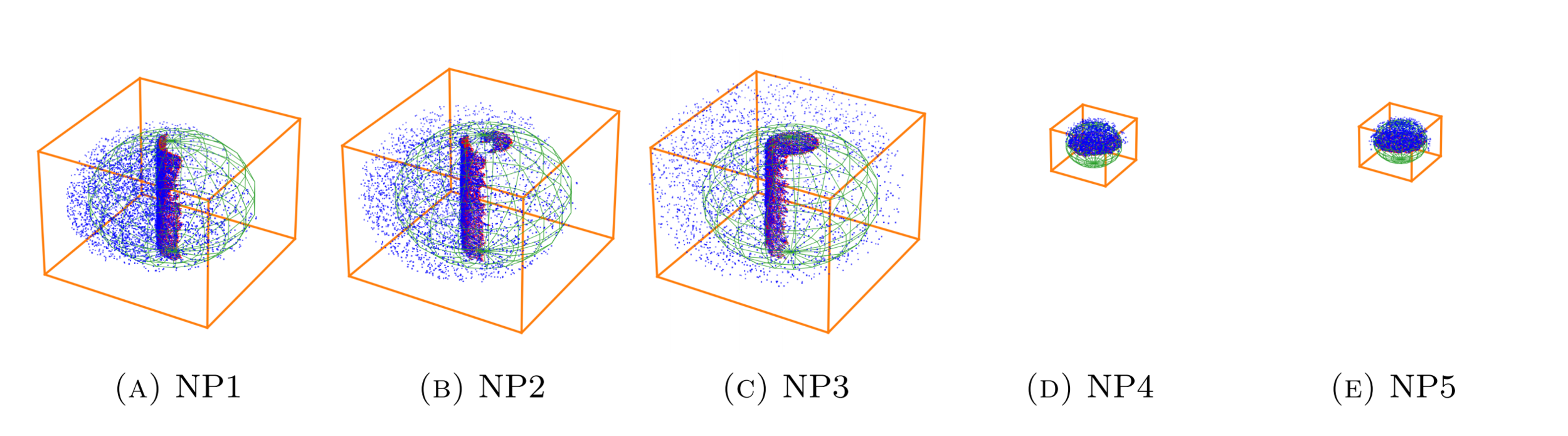
Ground-

Truth

To be solved...

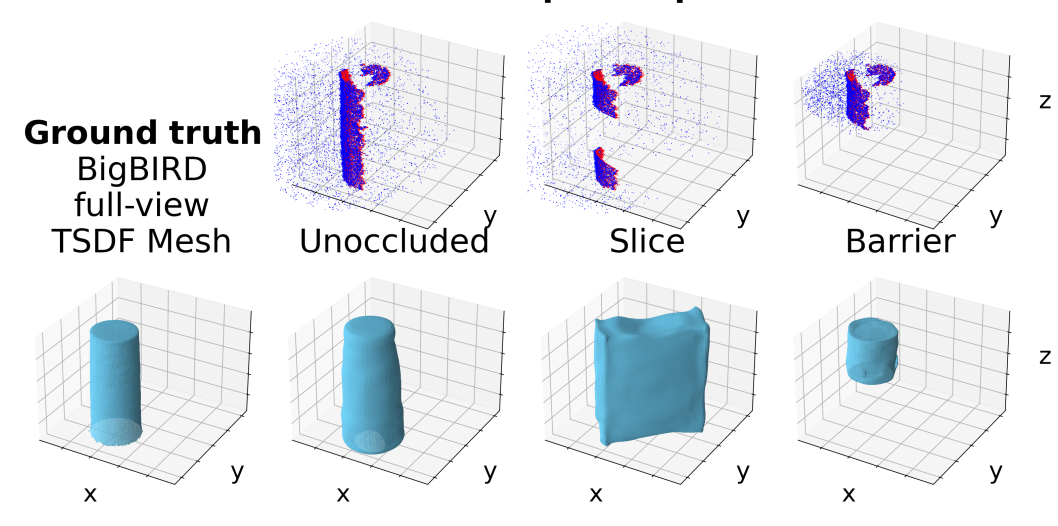
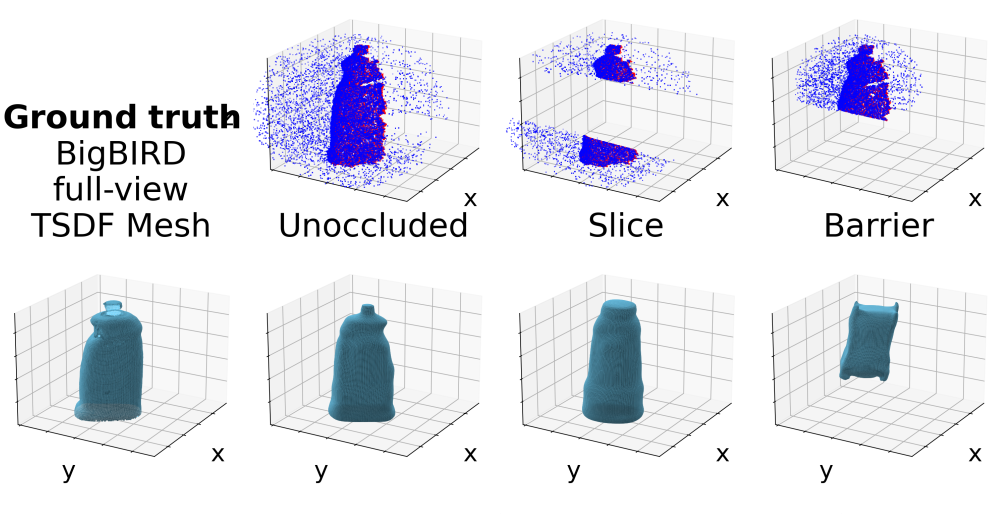
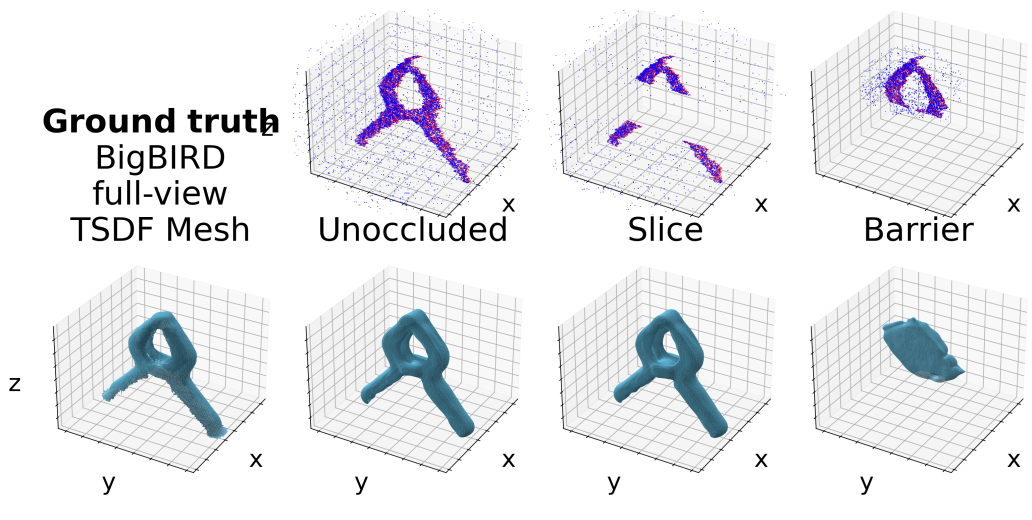
Testing Occlusions

Questions?

Tips?

https://s.ntnu.no/irobot

This is is the basis for a paper in the works.