

3DOR-2024
M
A
R
F
Towards Multi-View Consistency
in Neural Ray Fields
using Parametric Medial Surfaces
P
Parametric
Peder Bergebakken Sundt
Theoharis Theoharis
M
A
R
F
P
Parametric


3DOR-2024
Peder Bergebakken Sundt
Theoharis Theoharis
Towards Multi-View Consistency
in Neural Ray Fields
using Parametric Medial Surfaces
M
A
R
F
P
Medial
Atom
Ray
Field
Parametric


3DOR-2024
Peder Bergebakken Sundt
Theoharis Theoharis
Towards Multi-View Consistency
in Neural Ray Fields
using Parametric Medial Surfaces
A novel shape representation
Motivation
Fields
- Continuous
- Differentiable
- Different fields/signals are amenable to different novel applications
- Signed distance \(\to\) quick to traverse, watertight
- Generalized winding number \(\to\) self intersections, cloth
- Learned descriptor fields \(\to\) robotics
- Language embeddings \(\to\) semantic queries
Why make novel Neural Fields?
- Effective in Inverse Rendering and other problems in Visual Computing
like analysis-by-synthesis-
High compression ability
-
Able to learn mappings
previously considered ill-posed
(lottery ticket hypothesis)
-
-
New mappings enable new applications
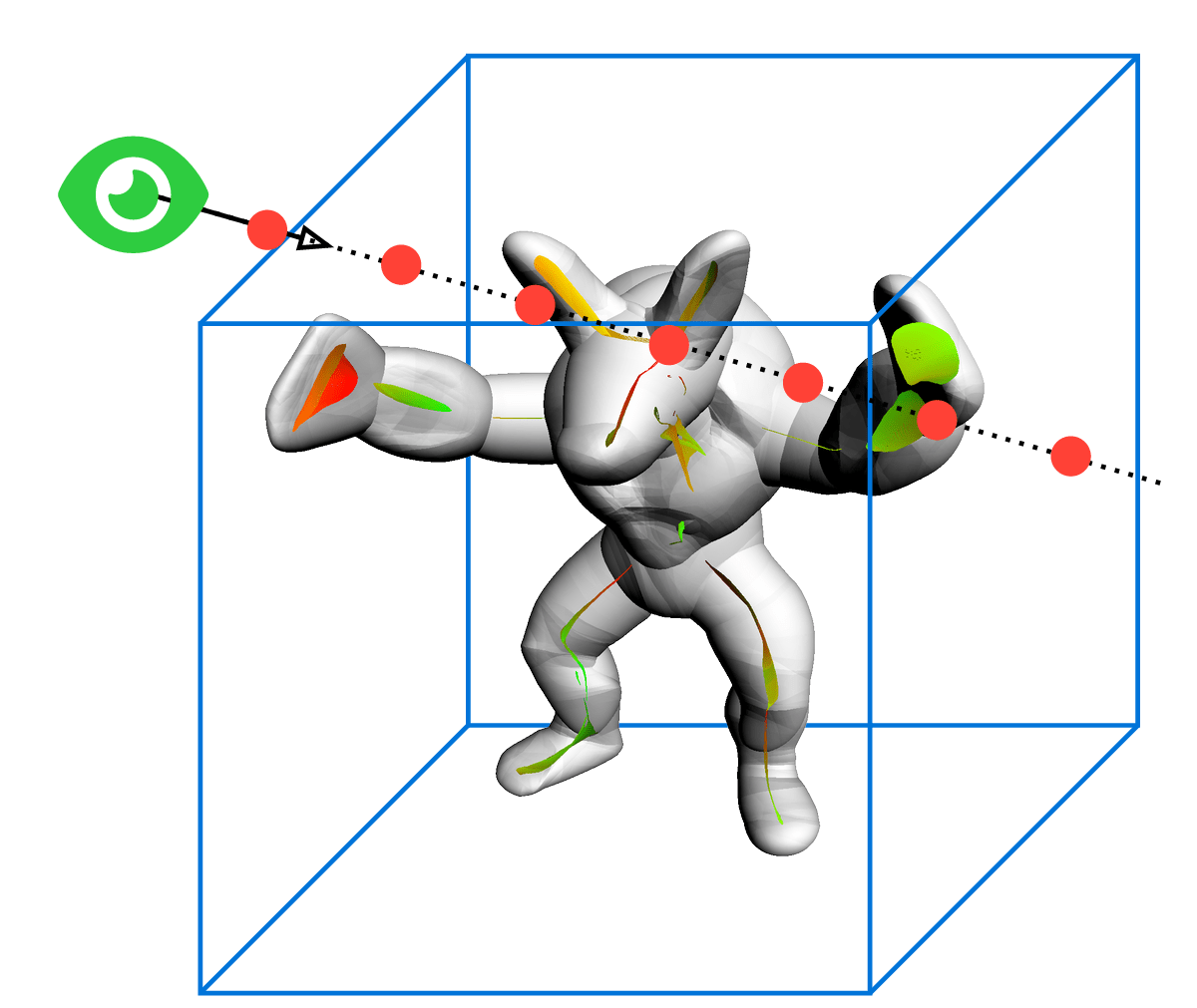
Why ray fields?
Neural fields are great at solving inverse rendering, but are slow to render
Directly predict
ray integral
Why ray fields?
Neural fields are great at solving inverse rendering, but are slow to render
Offline Tabulation
Precompute samples,
discretization artifacts (aliasing)
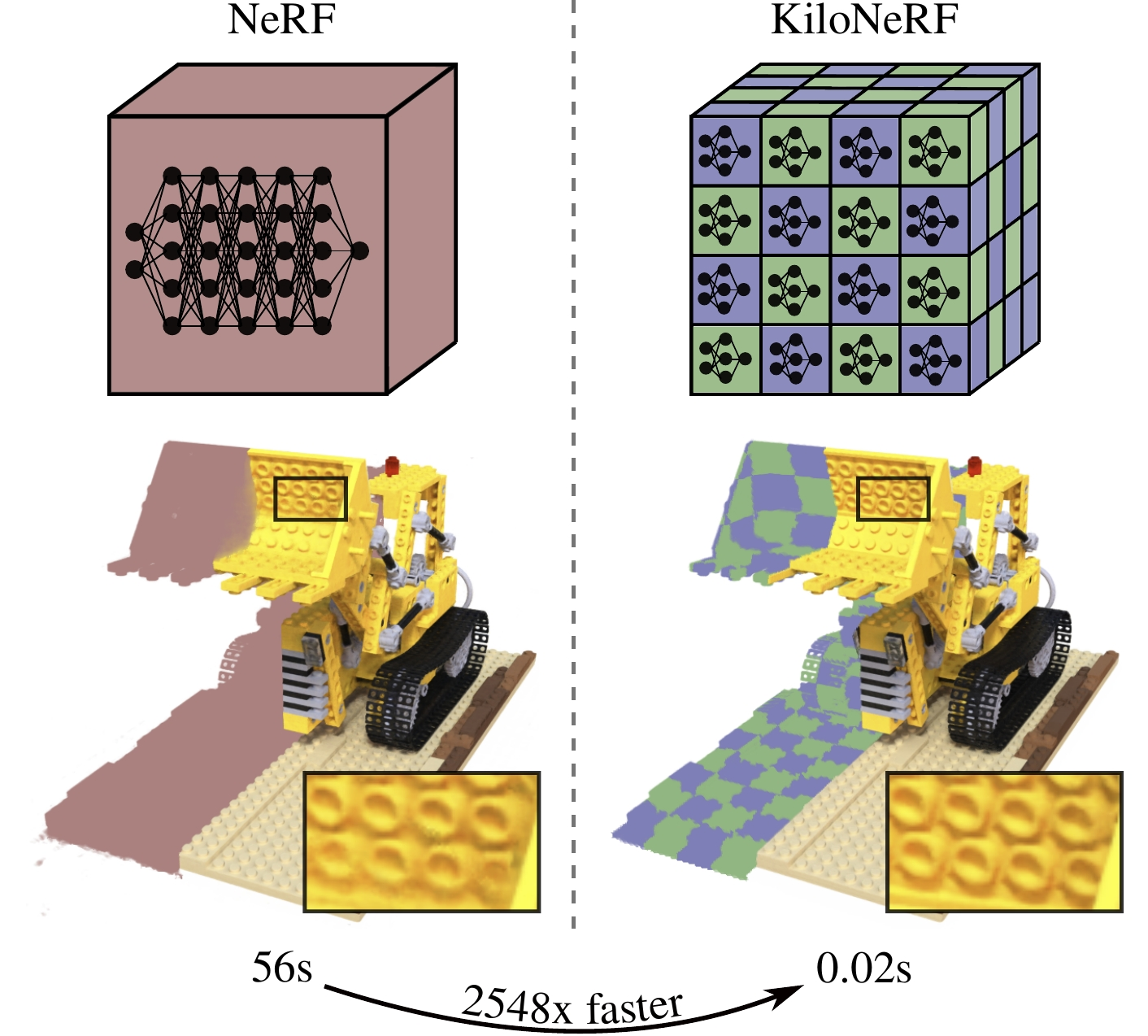
Hybrid methods
(Many small networks)
Cheaper samples, trade compute for memory, loss of global shape prior
Gaussian splatting
100x, View-dependent, no notion of surface or prior, hard to extract geometry
Learn heuristic field
(SDF)
10x reduction in samples, no transparent objects

Directly predict
ray integral
Neural fields are great at solving inverse rendering, but are slow to render
Why ray fields?

100x, View-
dependent, can represent both color and geometry, less studied

Offline Tabulation
Precompute samples,
discretization artifacts (aliasing)
Hybrid methods
(Many small networks)
Cheaper samples, trade compute for memory, loss of global shape prior


Gaussian splatting
100x, View-dependent, no notion of surface or prior, hard to extract geometry

Learn heuristic field
(SDF)
10x reduction in samples, no transparent objects

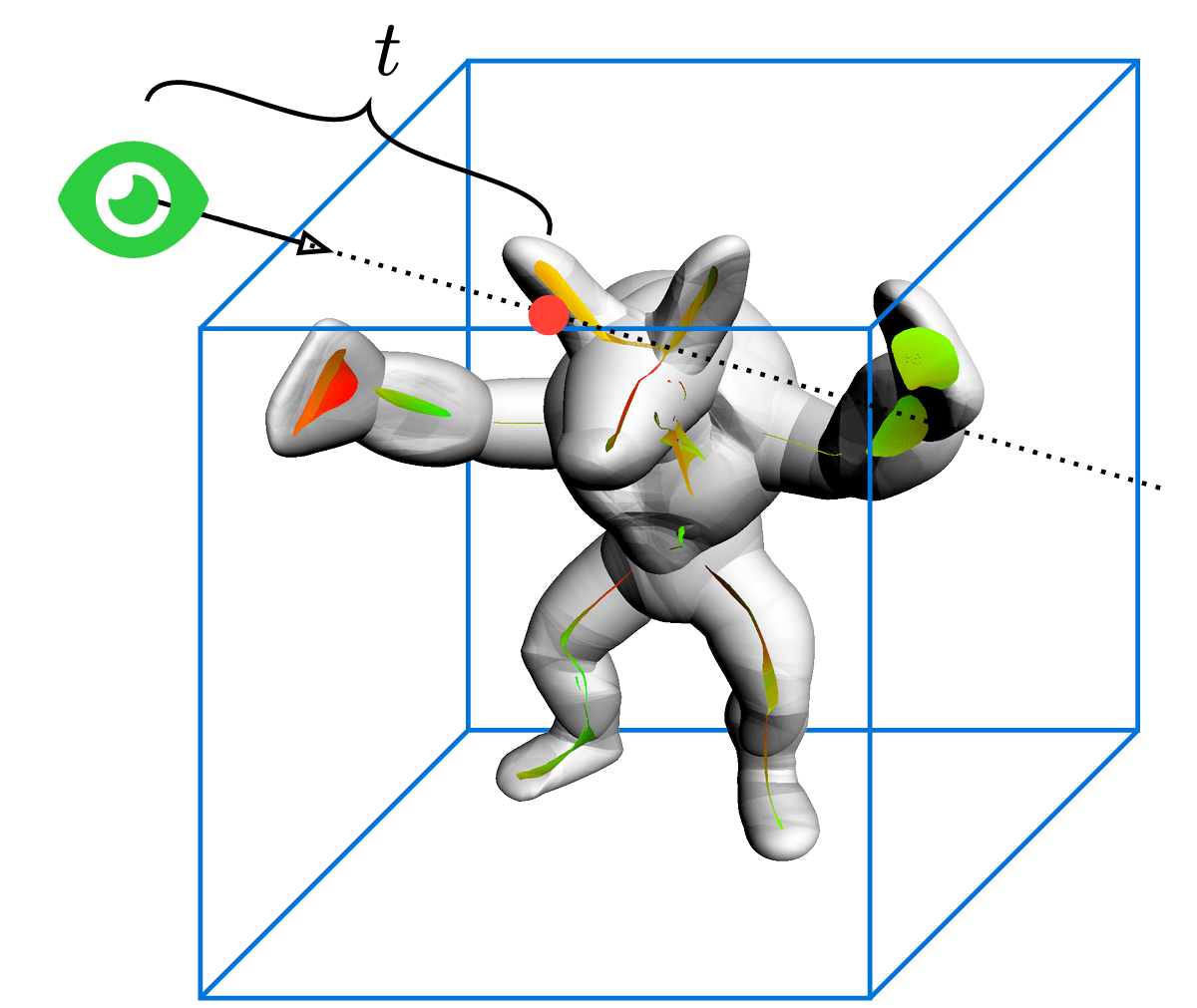
Cartesian Field functions (\(\mathbb R^3\to\mathcal X\))
require multiple sample along ray
While Ray Field functions (\(\mathcal R\to\mathcal X\))
map directly to the result
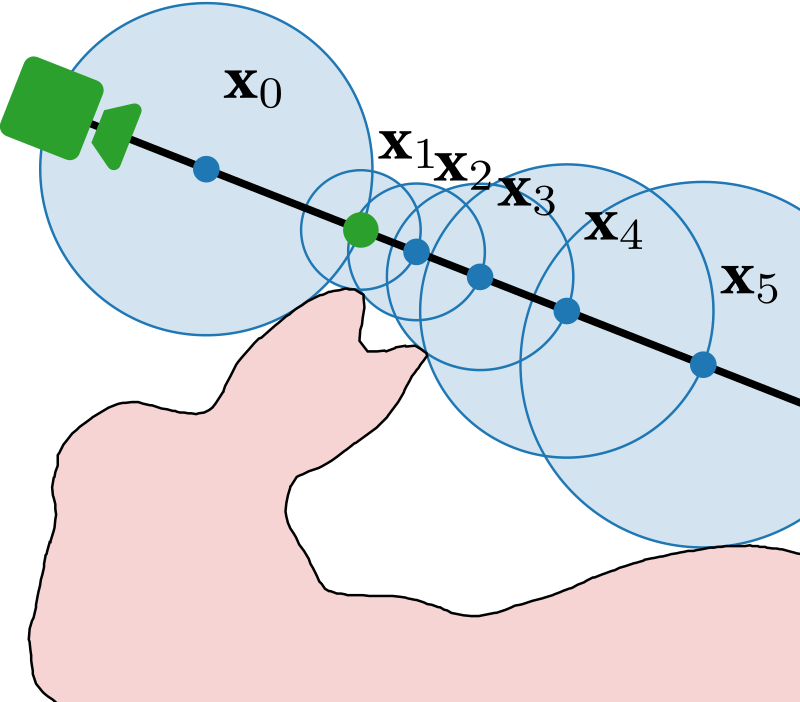
We build on the Medial Atom Ray Field (MARF)
Why build on MARF?
- Deals with ray field discontinuities
(Lipschitz bound) - Inherent multi-view consistency in reconstruction domain
- Emit cheap surface normals

Why build on MARF?

- Deals with ray field discontinuities
(Lipschitz bound) - Inherent multi-view consistency in reconstruction domain
- Emit cheap surface normals
Background




"Medial axis"
Set of maximally inscribed spheres


"Medial axis"
The set of maximally inscribed spheres, or "atoms"
Ridges of the distance transform



"Medial axis"
Ridges of the distance transform

The set of maximally inscribed spheres, or atoms
Set of points with two nearest neighbors



"Medial axis"
Set of points with two nearest neighbors


Ridges of the distance transform


Set of points with two nearest neighbors
"Medial axis"





MARF


MARF





?


(4 DoF)
(4 DoF)
?
View direction + xy in view plane
Atom/sphere
MARF
P


(4 DoF)
(4 DoF)
2 DoF!
Parametric surface
MARF
P
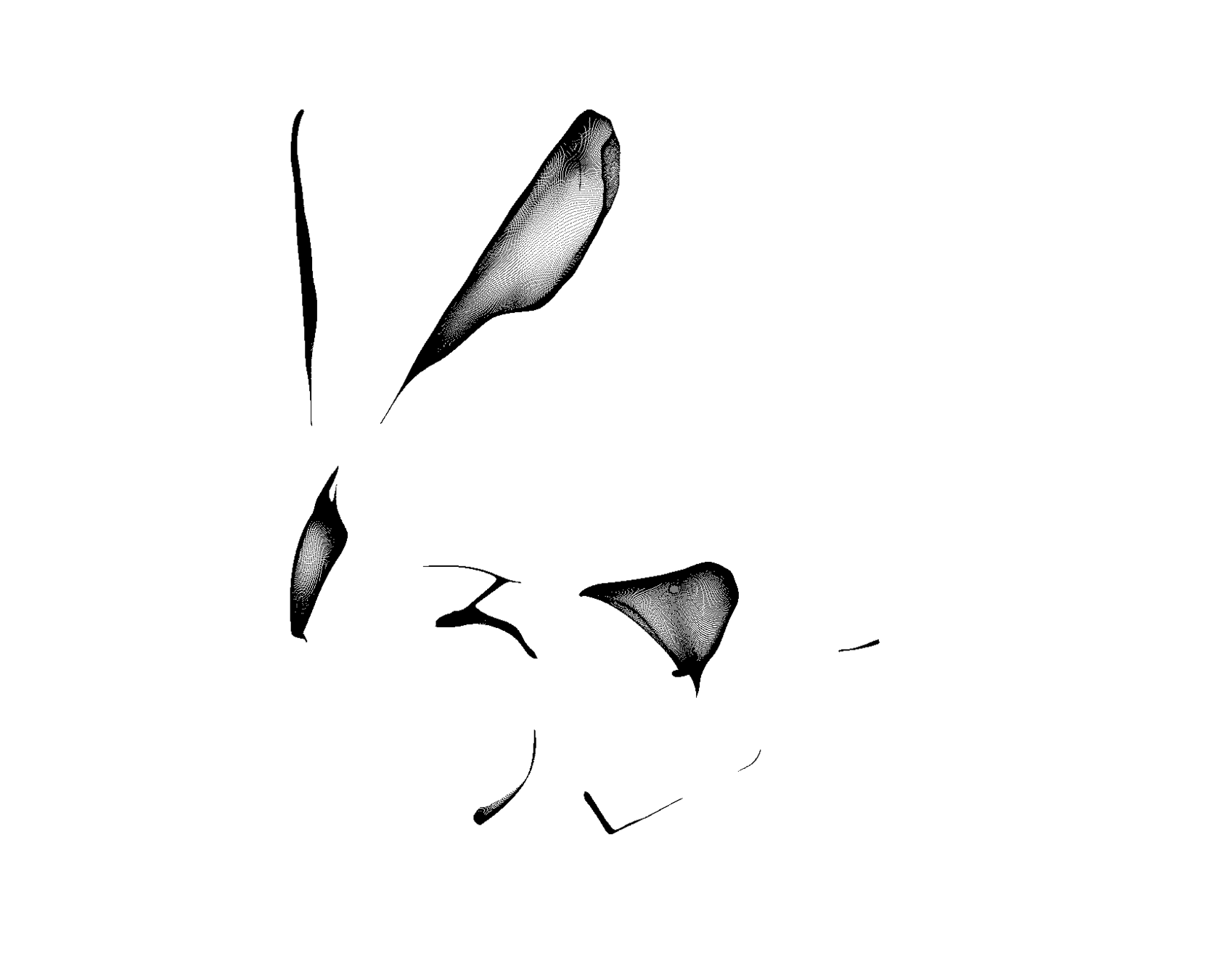
Zero Thickness by construction
More accurate medial surface
\(\Rightarrow\) More stable atoms

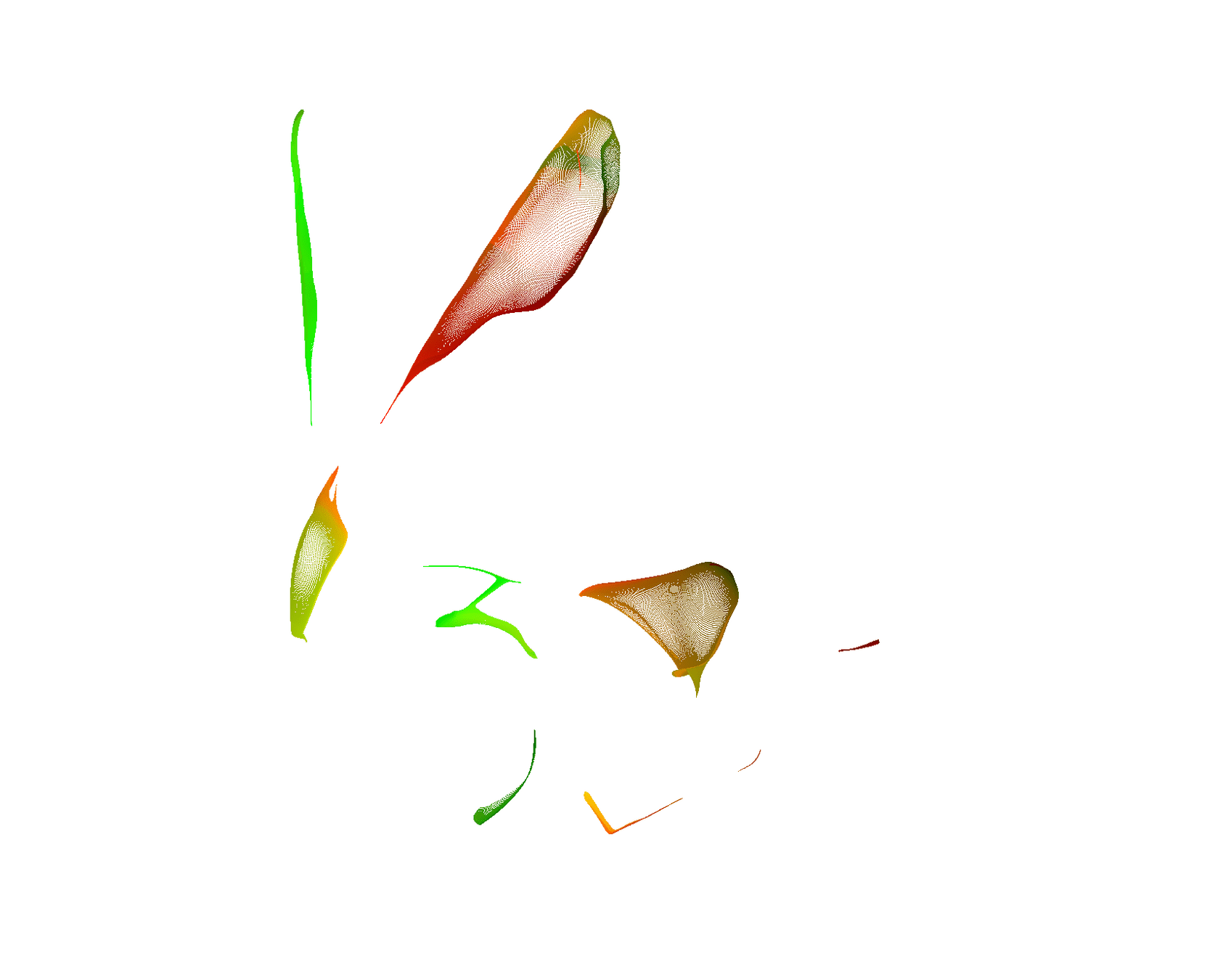
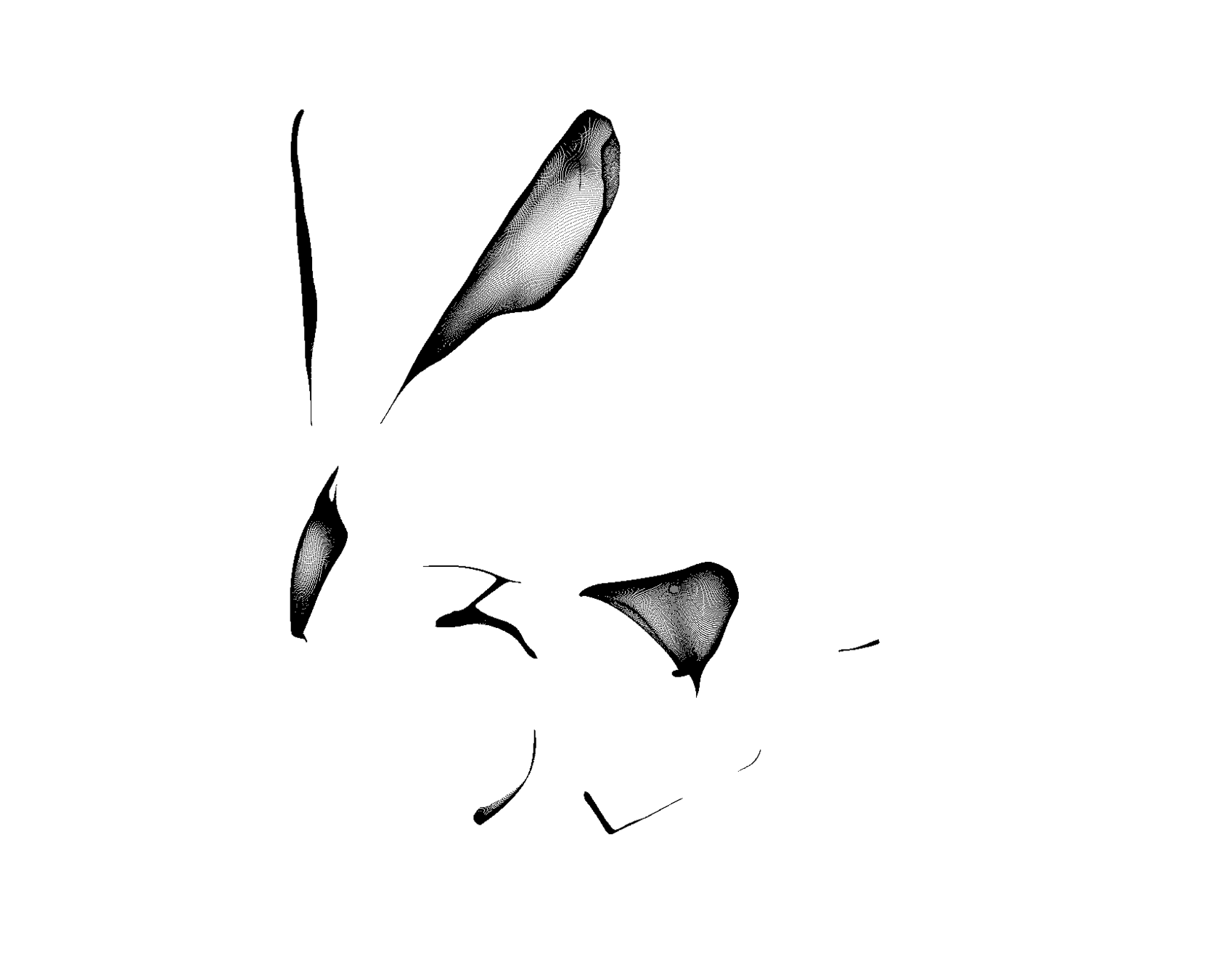
Architecture















MARF
P
Prior work
Ours















MARF
P
Prior work
Ours
Multiple MLP Heads
Block-diagonal matrices
Batched matrix multiplication















MARF
P
Prior work
Ours
Multiple MLP Heads
Block-diagonal matrices
Batched matrix multiplication















MARF
P
Prior work
Ours
Multiple MLP Heads
Block-diagonal matrices
Batched matrix multiplication
Fewer weights
Block diagonal
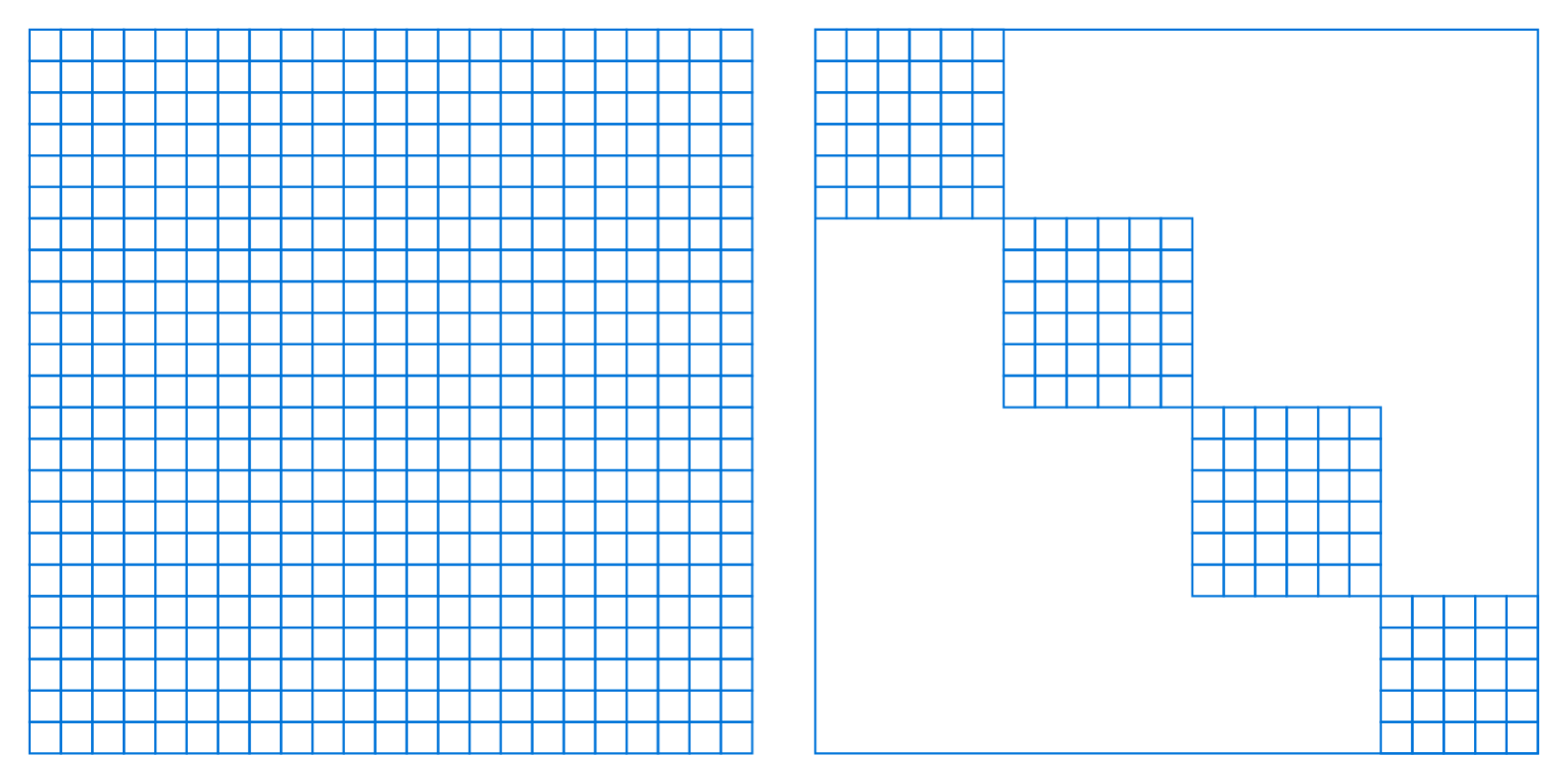
Fewer weights
Fully connected





Fewer weights
Block diagonal

Fully connected





Batched Matrix
Fewer weights
Block diagonal

Fully connected




Batched Matrix
We evaluate 4 different activations/nonlinearities
Evaluation
[1] Ba JL, Kiros JR, Hinton GE. Layer Normalization 2016.
[3] Ramasinghe S, Lucey S. Beyond Periodicity: Towards a Unifying Framework for Activations in Coordinate-MLPs. In: Avidan S, Brostow G, Cissé M, Farinella GM, Hassner T, editors. Computer Vision – ECCV 2022, Cham: Springer Nature Switzerland; 2022, p. 142–58.
[2] Sitzmann V, Martel JNP, Bergman AW, Lindell DB, Wetzstein G. Implicit Neural Representations with Periodic Activation Functions. Proc. NeurIPS, 2020
[4] Saragadam V, LeJeune D, Tan J, Balakrishnan G, Veeraraghavan A, Baraniuk RG. WIRE: Wavelet Implicit Neural Representations, 2023, p. 18507–16

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
We evaluate 4 different activations/nonlinearities
Evaluation
First we try each on the prior architecture

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth
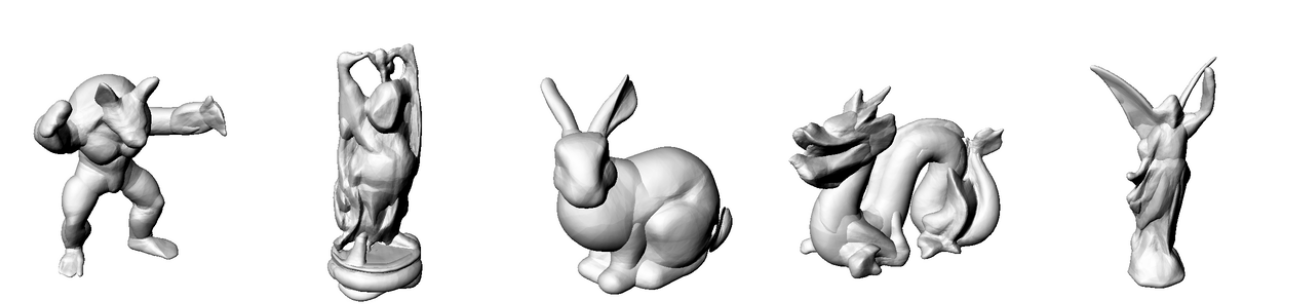

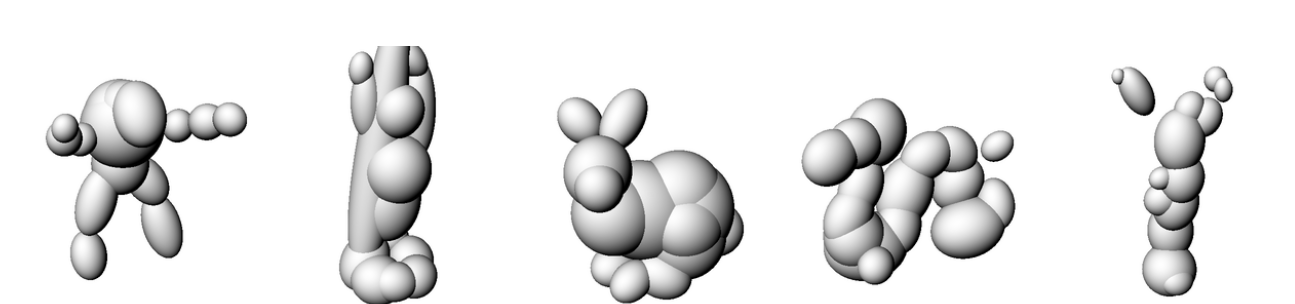

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth
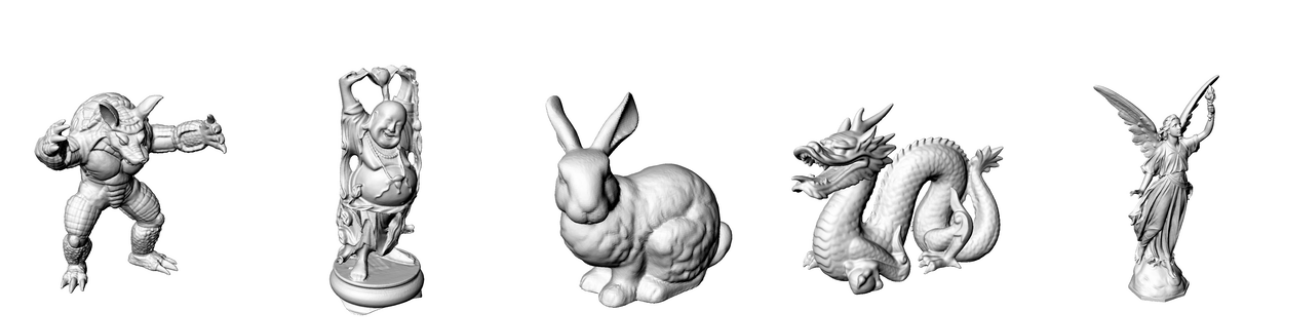

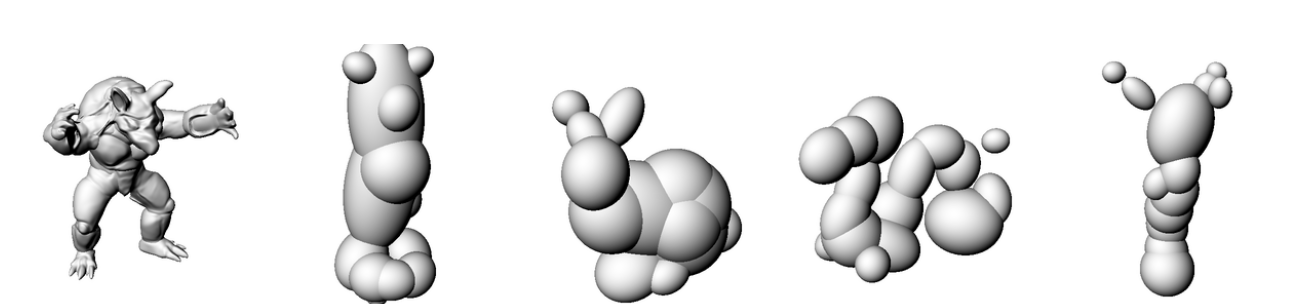
ReLU [1]

ReLU [1]

ReLU [1]

ReLU [1]














Ray decoder
Surface decoder

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth

ReLU [1]

ReLU [1]

ReLU [1]

ReLU [1]















Ray decoder

WIRE [4]
Surface decoder

ReLU [1]

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth

ReLU [1]

ReLU [1]

ReLU [1]

ReLU [1]

SIREN [2]

SIREN [2]

SIREN [2]

SIREN [2]















Ray decoder

WIRE [4]
Surface decoder

ReLU [1]

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth

ReLU [1]

ReLU [1]

ReLU [1]

ReLU [1]
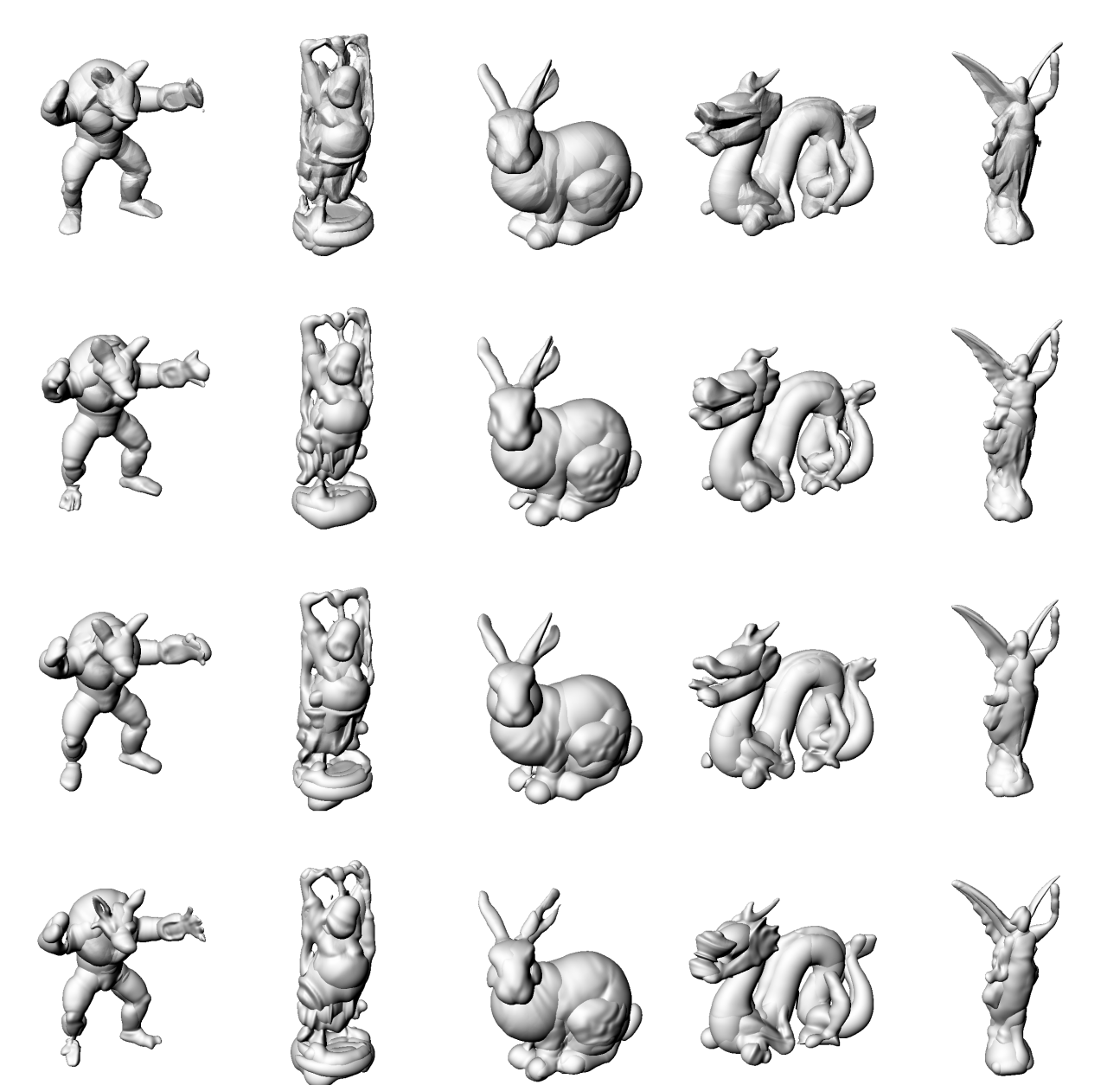

SIREN [2]

SIREN [2]

SIREN [2]

SIREN [2]
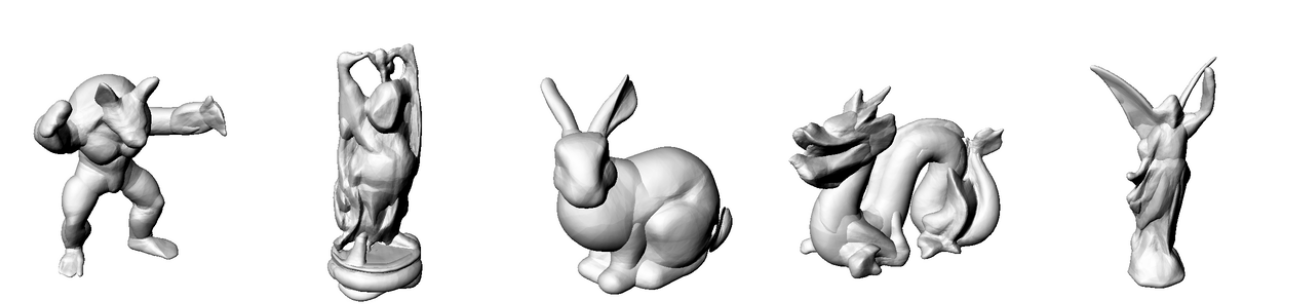

ReLU [1]

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth
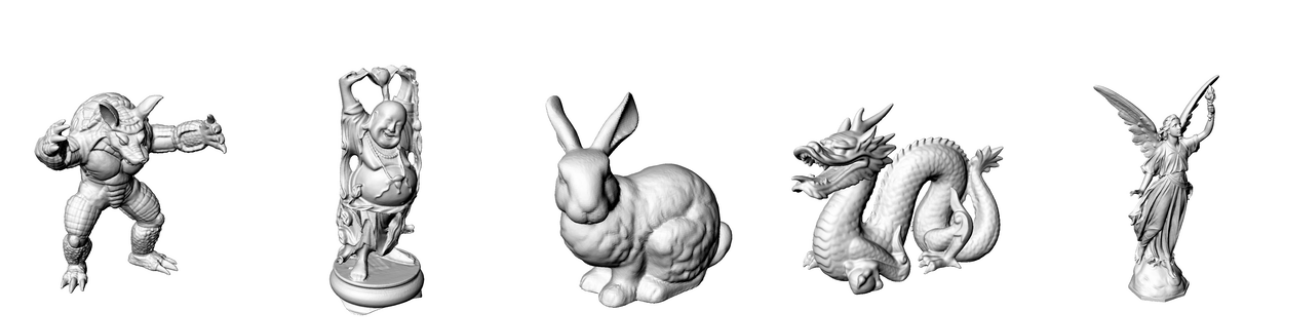

ReLU [1]

ReLU [1]

ReLU [1]

ReLU [1]

SIREN [2]

SIREN [2]

SIREN [2]

SIREN [2]
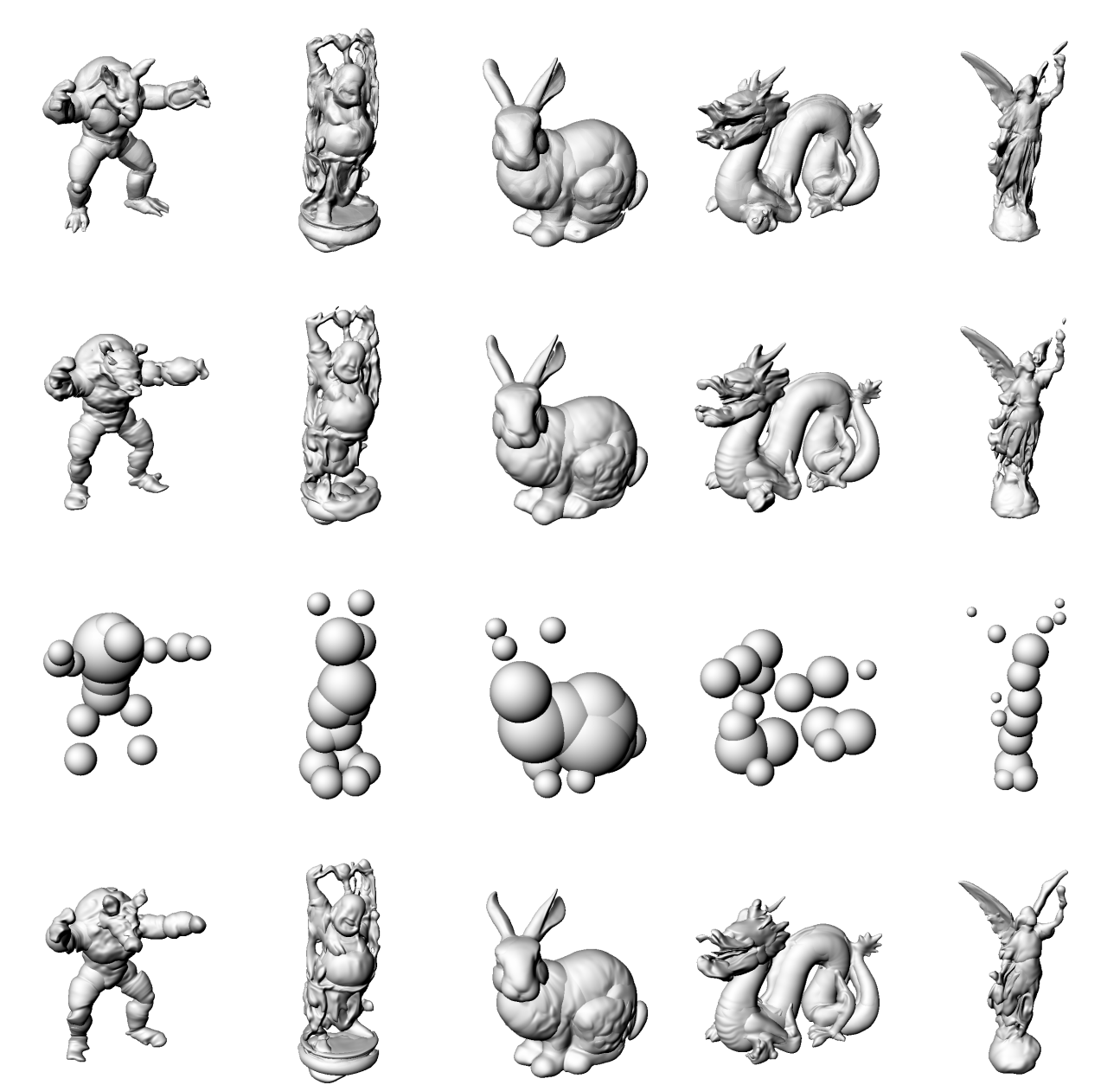

Gauss [3]

Gauss [3]

Gauss [3]

Gauss [3]

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth
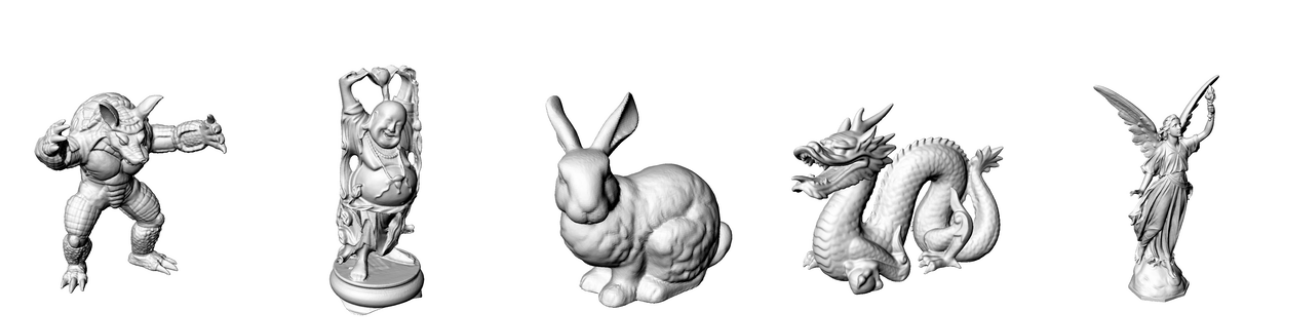

SIREN [2]

SIREN [2]

SIREN [2]

SIREN [2]

Gauss [3]

Gauss [3]

Gauss [3]

Gauss [3]

WIRE [4]

WIRE [4]

WIRE [4]

WIRE [4]
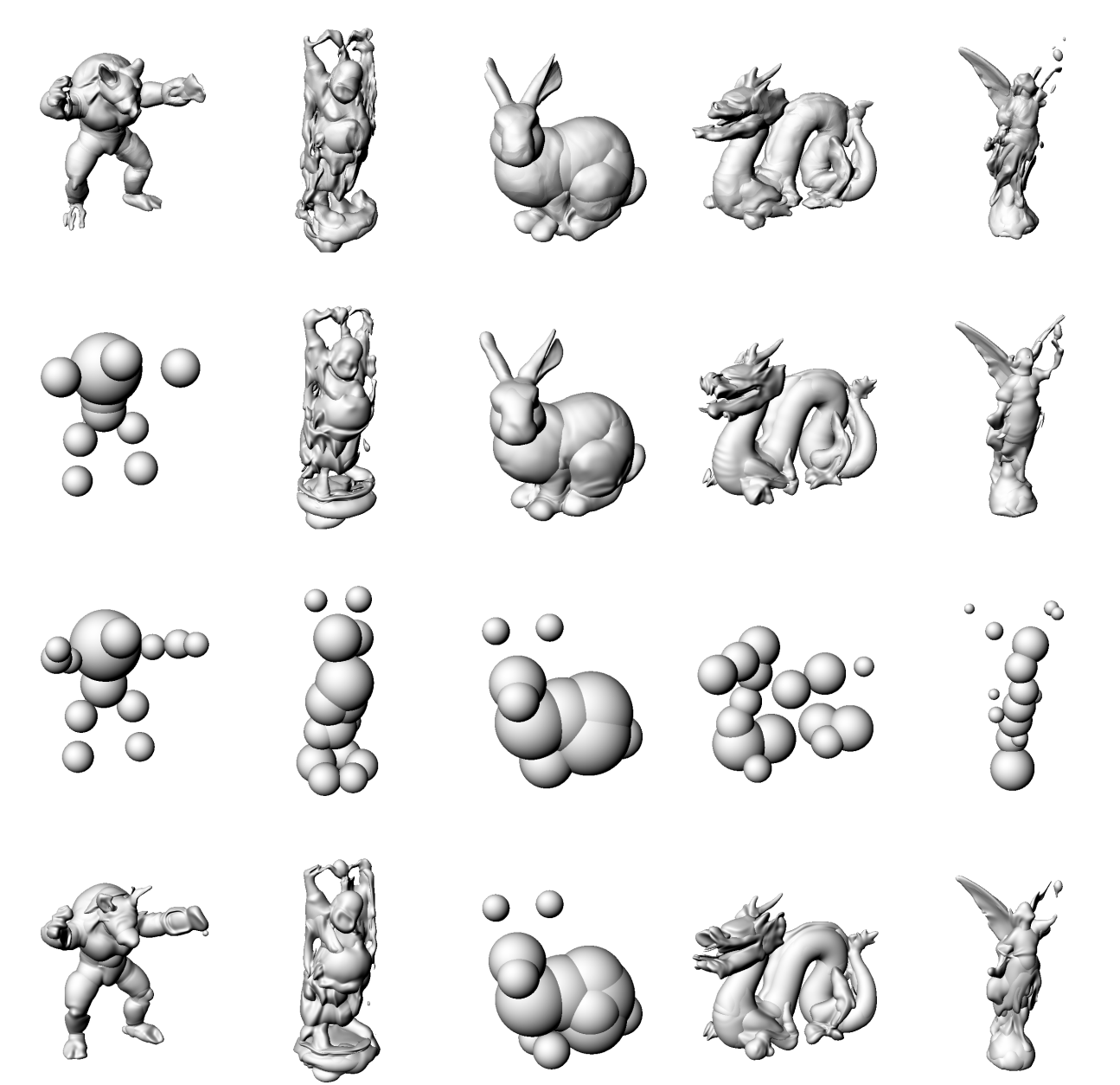

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth
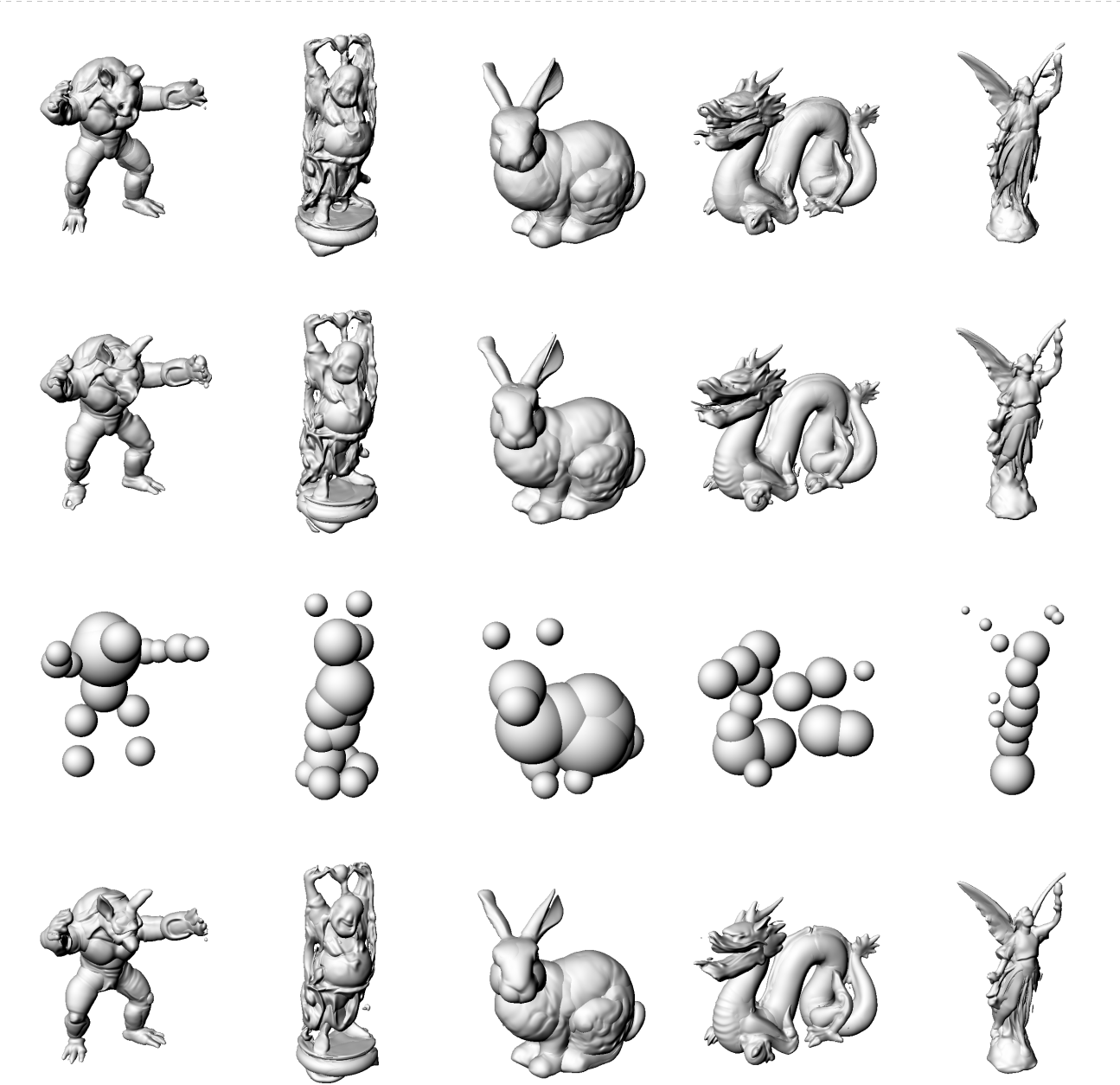

Gauss [3]

Gauss [3]

Gauss [3]

Gauss [3]

WIRE [4]

WIRE [4]

WIRE [4]

WIRE [4]

ReLU [1]

SIREN [2]

Gauss [3]

WIRE [4]
Ground
Truth
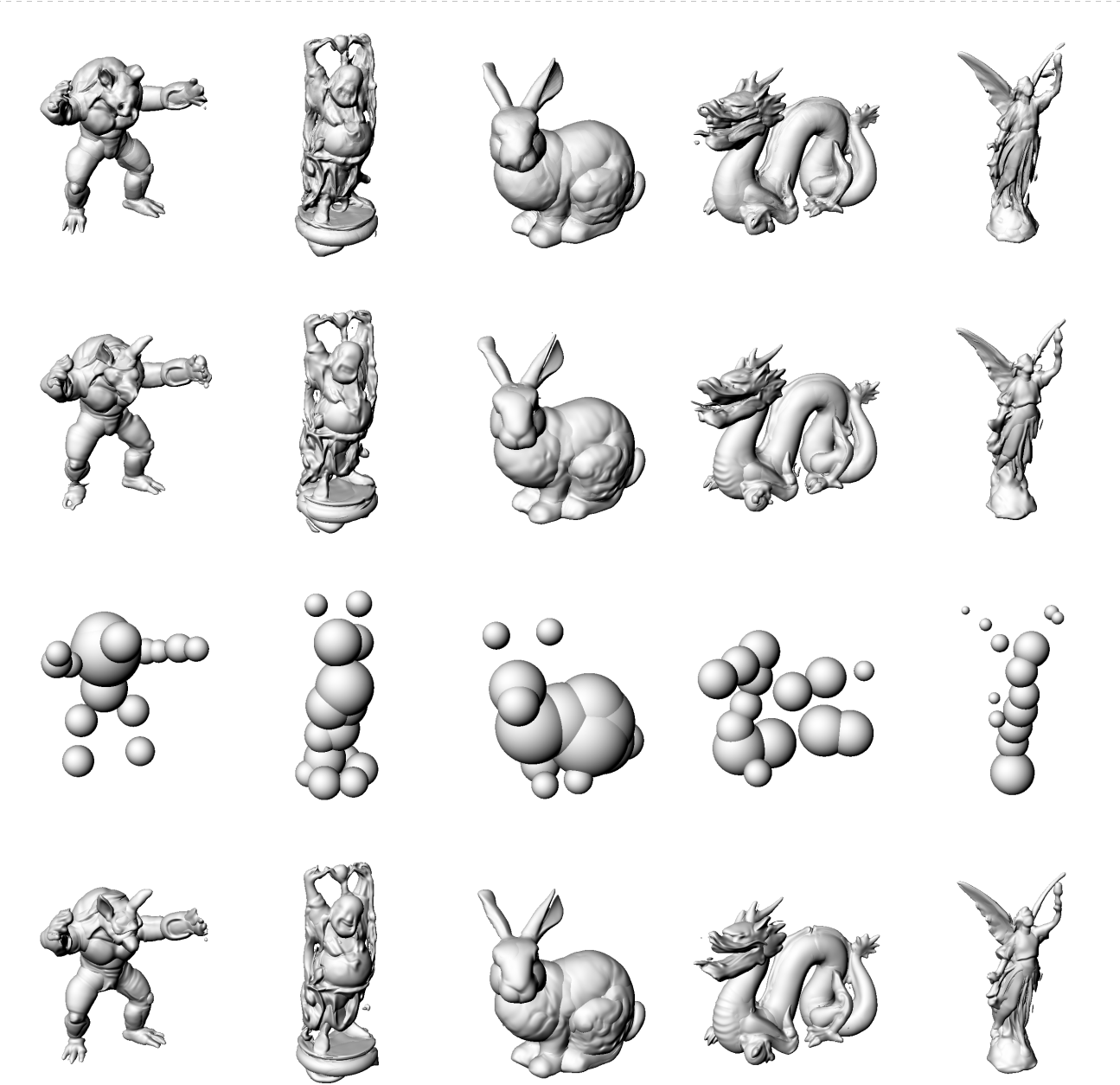

Gauss [3]

WIRE [4]

WIRE [4]

WIRE [4]

WIRE [4]











MARF
arch is
unstable











MARF
arch is
unstable











MARF
arch is
unstable














>>> # (BATCH, N_BLOCKS, INTER-BLOCK WIDTH)
>>> input = torch.empty(128, 8, 8)
>>> weight = torch.empty(8, 8, 8)
>>> output = torch.einsum("...ij,ijk->...ik", input, weight)
>>> output.shape
torch.Size([128, 8, 8])
>>> output.stride()
(8, 1024, 1)
>>> torch.empty(128, 8, 8).stride()
(64, 8, 1)







>>> # (BATCH, N_BLOCKS, INTER-BLOCK WIDTH)
>>> input = torch.empty(128, 8, 8)
>>> weight = torch.empty(8, 8, 8)
>>> output = torch.einsum("...ij,ijk->...ik", input, weight)
>>> output.shape
torch.Size([128, 8, 8])
>>> output.stride()
(8, 1024, 1)
>>> torch.empty(128, 8, 8).stride()
(64, 8, 1)







>>> # (BATCH, N_BLOCKS, INTER-BLOCK WIDTH)
>>> input = torch.empty(128, 8, 8)
>>> weight = torch.empty(8, 8, 8)
>>> output = torch.einsum("...ij,ijk->...ik", input, weight)
>>> output.shape
torch.Size([128, 8, 8])
>>> output.stride()
(8, 1024, 1)
>>> torch.empty(128, 8, 8).stride()
(64, 8, 1)
>>> torch.tensor( 1 + 2j ).to(torch.float16)
UserWarning: Casting complex values to real discards the imaginary part
tensor(1., dtype=torch.float16)







>>> # (BATCH, N_BLOCKS, INTER-BLOCK WIDTH)
>>> input = torch.empty(128, 8, 8)
>>> weight = torch.empty(8, 8, 8)
>>> output = torch.einsum("...ij,ijk->...ik", input, weight)
>>> output.shape
torch.Size([128, 8, 8])
>>> output.stride()
(8, 1024, 1)
>>> torch.empty(128, 8, 8).stride()
(64, 8, 1)
>>> torch.tensor( 1 + 2j ).to(torch.float16)
UserWarning: Casting complex values to real discards the imaginary part
tensor(1., dtype=torch.float16)
Initialization
Surface points
Surface clouds are simple to compute from depth scans or SfM landmarks
Surface points
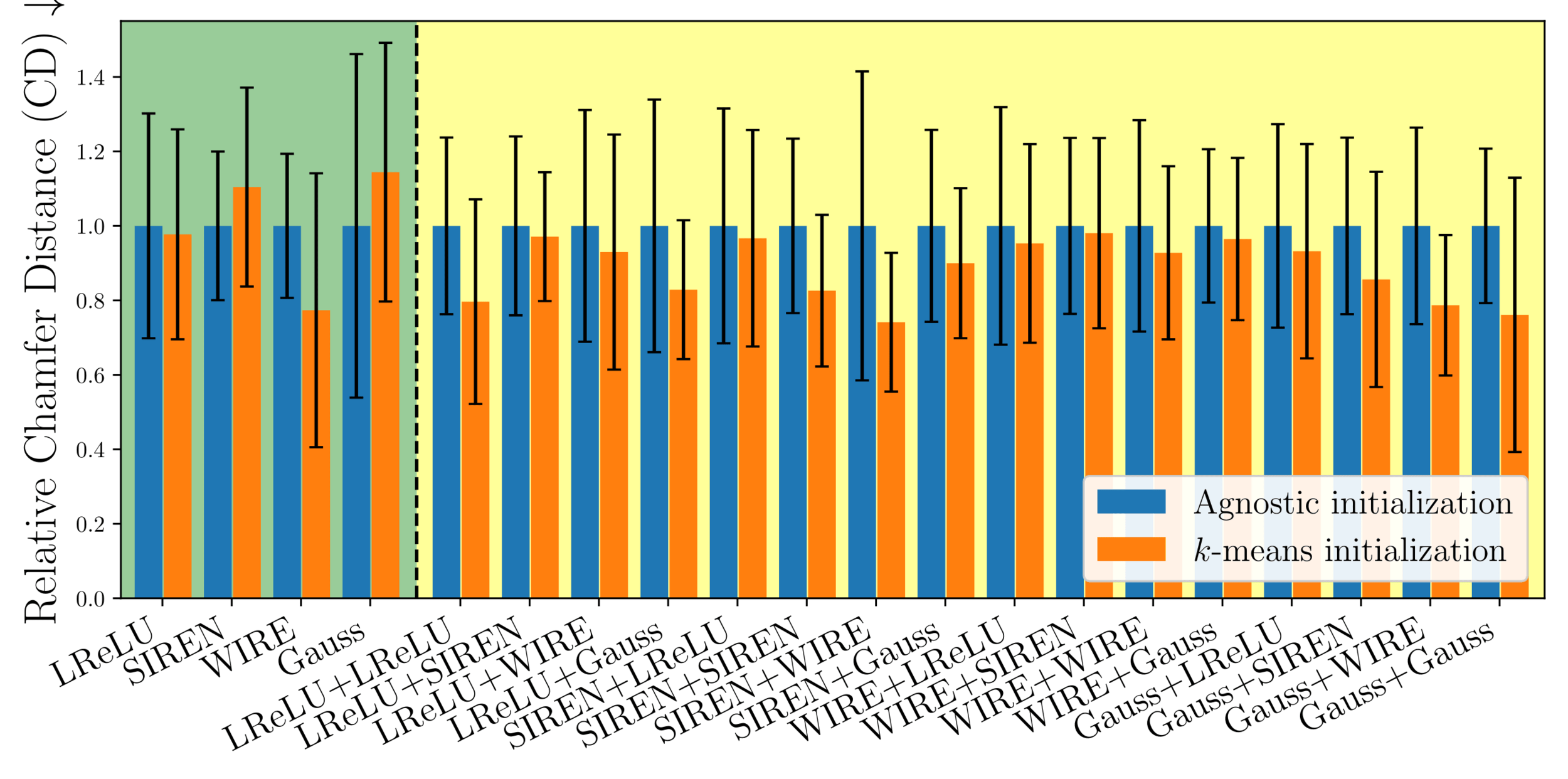
Agnostic (MARF)
K-Means Clustering (Ours)
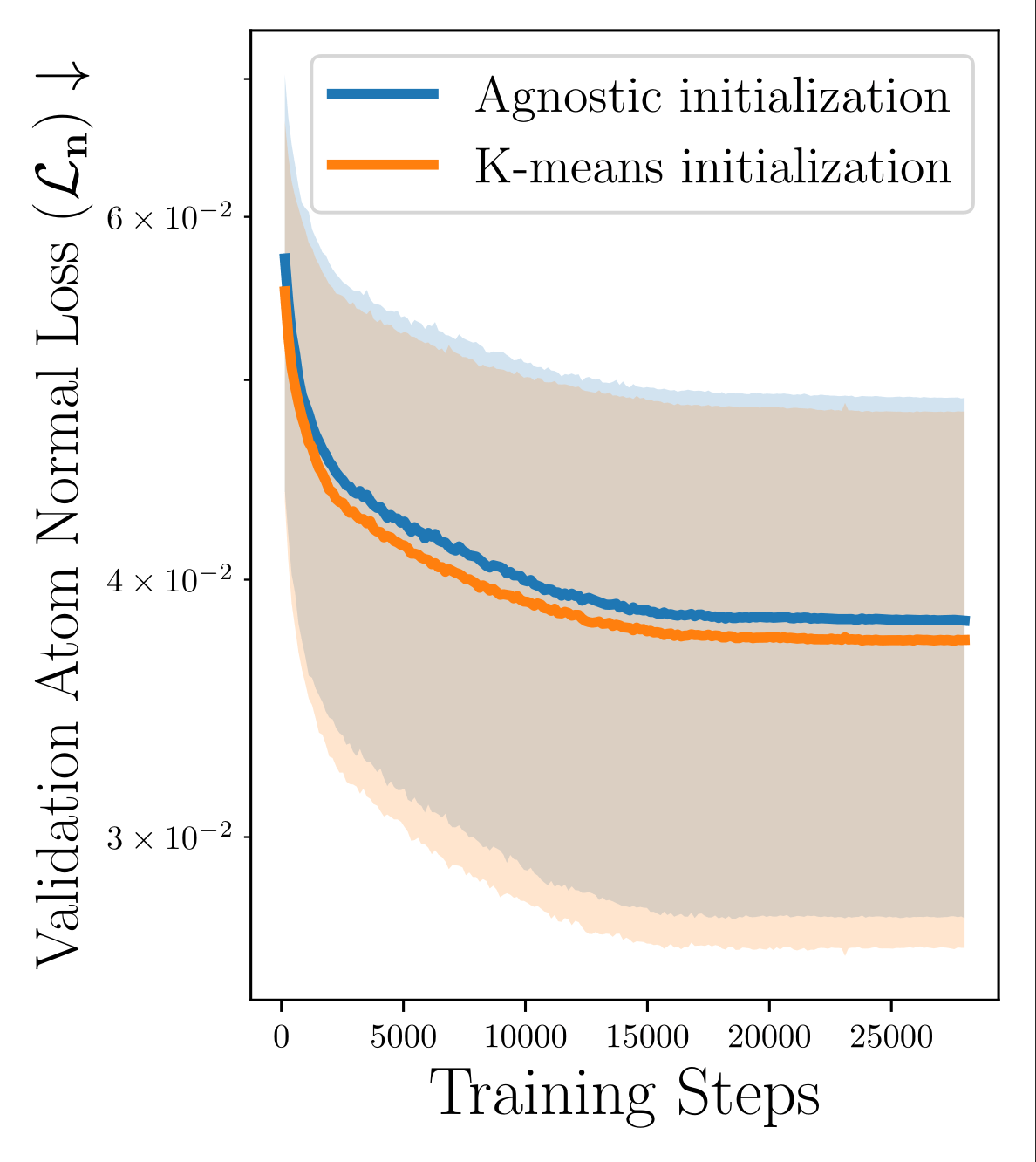
Average over 80 runs, for each shape activation function
MARFs
PMARFs
Non-ReLU
too unstable
to get a good read
Strict improvement
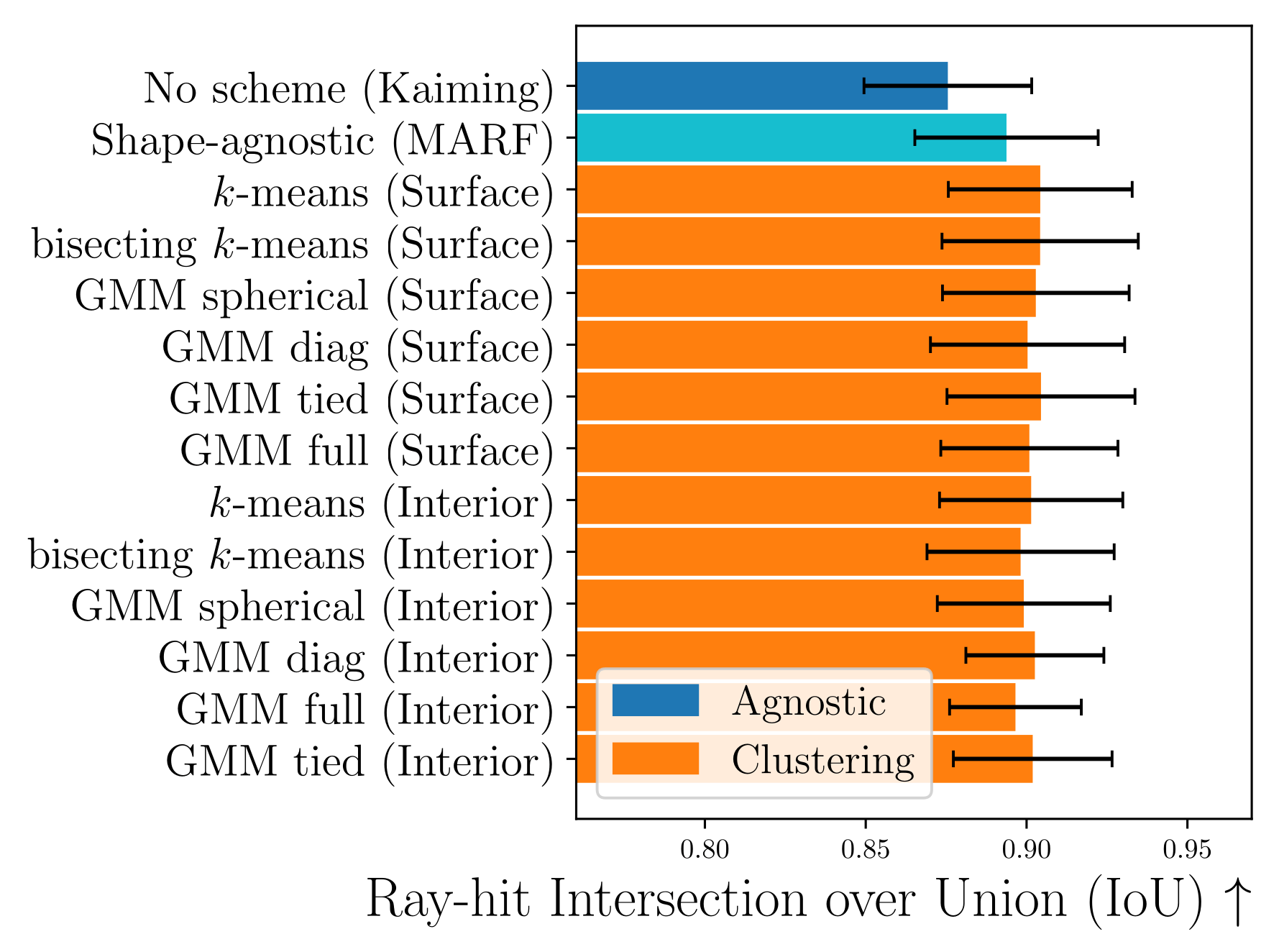
Exploring various unsupervised clustering algorithms
Surface points
Interior Volume points
(Requires full view, and is too expensive to compute in a real-time scenario)

Sparse-view Scenarios
35 training views, 15 validation views
~4000 test views
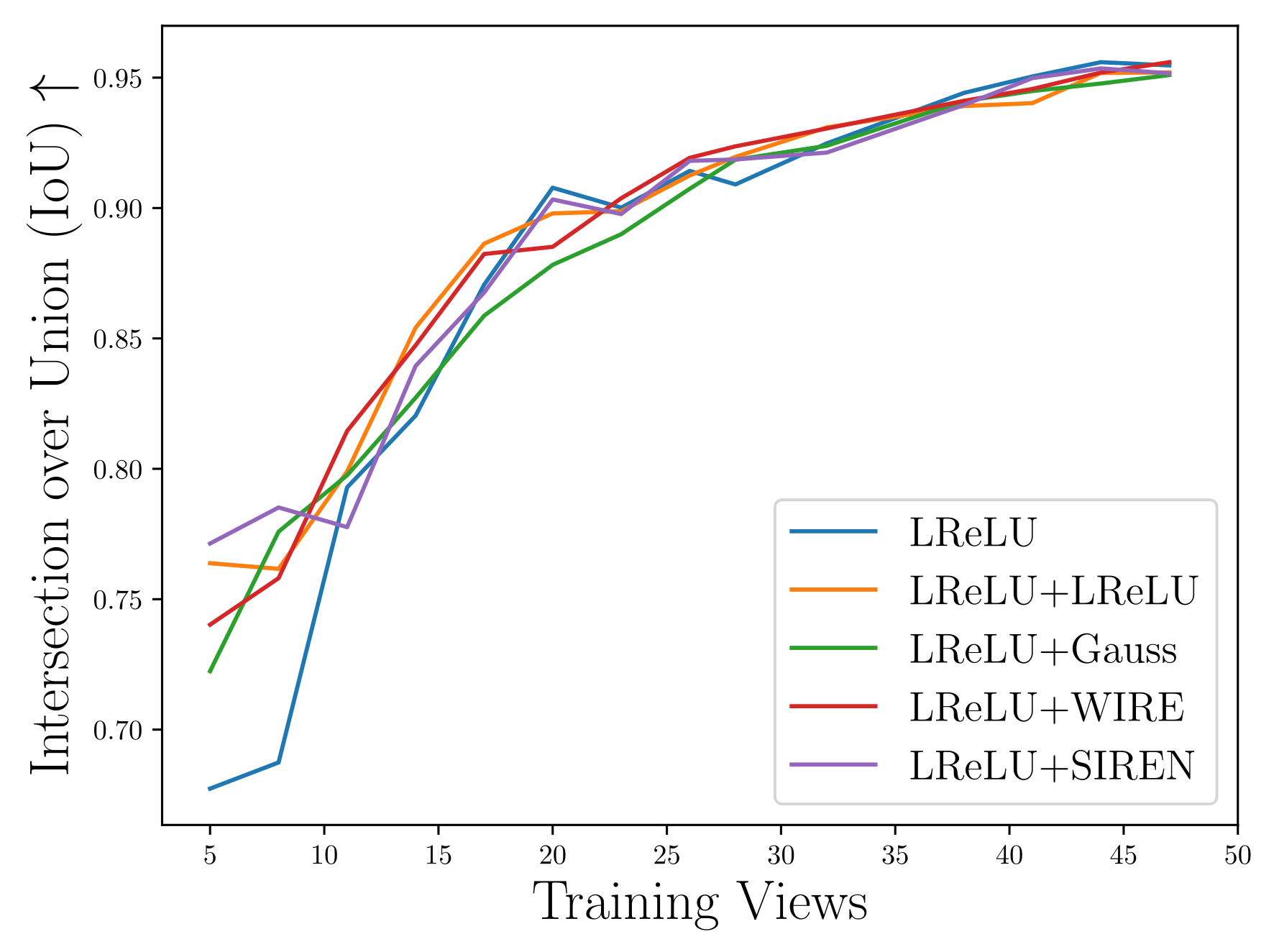
Sparse-view Scenarios

PMARFs
MARF
Sparse-view Scenarios
Conclusion
We present PMARF a Neural Ray Field with
- Improved multi-view consistency
- Improved reconstruction fidelity
- A lower parameter count, and that
- Performs well with more advanced nonlinearities

Thank you
Questions?