Causal Inference

Business Analytics

Motivation

We all intuitively understand what it means for something to Cause something else

Many of the questions that we're interested in are causal in nature

  • What is the impact of a remote work policy on stock price?
  • What is the effect of crime rates on hotel occupancy?
  • What's the impact of inflation on public education spending?
  • What's the return to a private secondary education compared to a public secondary education?

Causal Inference as A Missing Data Problem

Context

What is the effect of taking BA222 versus the Excel Equivalent on Earnings Five Years after Graduation?

Notation

\tilde{Y}_i(1) - \tilde{Y}_i(0)

Five Year Post College Earnings if the person took BA222

Five Year Post College Earnings if the person did not take BA222

Estimand

\mathbb{E}[\tilde{Y}_i(1) - \tilde{Y}_i(0)]

Difference in means

Idea

Approximate the Average Treatment Effect by comparing the earnings of students who took BA222 with the earnings of those who took the Excel Equivalent

\mathbb{E}[Y_i \vert D_i=1] - \mathbb{E}[Y_i \vert D_i=0]

The Average Earnings for those who took BA222

The Average Earnings for those who took the excel equivalent

\mathbb{E}[Y_i \vert D_i=1] - \mathbb{E}[Y_i \vert D_i=0]
= \mathbb{E}[\tilde{Y}_i(1) \vert D_i=1] - \mathbb{E}[\tilde{Y}_i(0) \vert D_i=0]

Difference-in-Means

= \underbrace{\mathbb{E}[\tilde{Y}_i(1) \vert D_i=1] - \mathbb{E}[\tilde{Y}_i(0) \vert D_i=1]}
+ \ \underbrace{\mathbb{E}[\tilde{Y}_i(0) \vert D_i=1] - \mathbb{E}[\tilde{Y}_i(0) \vert D_i=0]}

Difference-in-Means

Average Treatment on the Treated

Selection Bias

=
+

Python Exercise

means = '###FILL THIS IN###'.mean()
print(f'The difference in means is: ${means.loc[1.0] - means.loc[0.0]:.0f}')

Difference-in-Means

treated_df = df['###FILL THIS IN###']
ATT = treated_df['###FILL THIS IN###'].mean() - treated_df['###FILL THIS IN###'].mean()
print(ATT)

Average Treatment on the Treated

means_y0 = df.groupby('###FILL THIS IN####'].mean()
selction_bias = means_y0.loc[1.0] - means_y0[0.0]
print(selction_bias)

Selection Bias

The need for controls

Idea # 2

Instead of taking the difference between treated and control groups, let's average local differences between treated and control groups

Summary (thus far)

\textrm{Causal Inference is a Missing Data Problem}
1
\textrm{Difference-in-Means} \ = \ \textrm{Avg Treatment Treated} \ + \ \textrm{Selection Bias}
2

Local with respect to features/ independent variables

(1) Take difference-in-means within each group

\mathbb{E}[Y_i \vert X_i = x_j, D=1] - \mathbb{E}[Y_i \vert X_i = x_j, D=0]
\mathbb{E}_x\big[\mathbb{E}[Y_i \vert X_i = x_j, D=1] - \mathbb{E}[Y_i \vert X_i = x_j, D=0]\big]

(2) Take the average differences

Idea # 2

X_i

Let's assume we observe a Questrom Concentration

x_0
x_1
x_2
x_3
x_4

Accounting

Finance

Marketing

Real Estate

Strategy

Under what conditions is this a good idea?

\mathbb{E}[Y_i \vert X_i = x_j, D=1] - \mathbb{E}[Y_i \vert X_i = x_j, D=0]
= \mathbb{E}[\tilde{Y}_i(1) \vert X_i = x_j, D=1] - \mathbb{E}[\tilde{Y}_i(0) \vert X_i = x_j, D=0]
= \mathbb{E}[\tilde{Y}_i(1) - \tilde{Y}_i(0) \vert X_i = x_j]
= \mathbb{E}[\tilde{Y}_i(1) \vert X_i = x_j] - \mathbb{E}[\tilde{Y}_i(0) \vert X_i = x_j]

Key Assumption

"Within each concentration, the decision about to take BA22 is independent of the potential outcomes"

Python Exercise

estimate = 0 
variables = ['X0', 'X1', 'X2', 'X3', 'X4']
for var in variables:
  df_temp = df['###FILL THIS IN###']
  weight = len(df_temp) / len(df)
  effect = df_temp.groupby('Treatment')['Outcome'].mean().loc[1.0] - df_temp.groupby('Treatment')['Outcome'].mean().loc[0.0]
  estimate += weight*effect
print(estimate)

Average Within Group Difference in Means

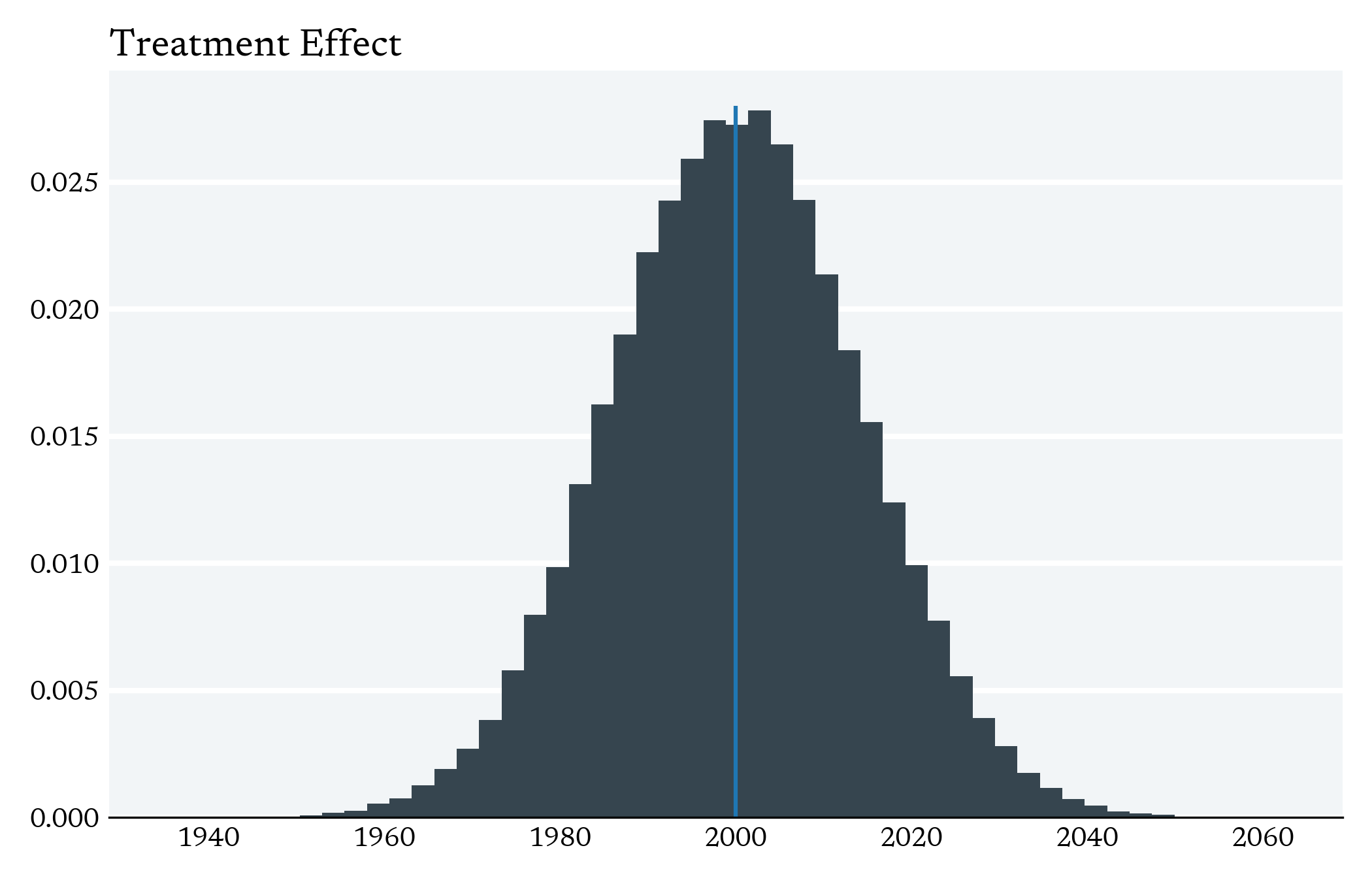
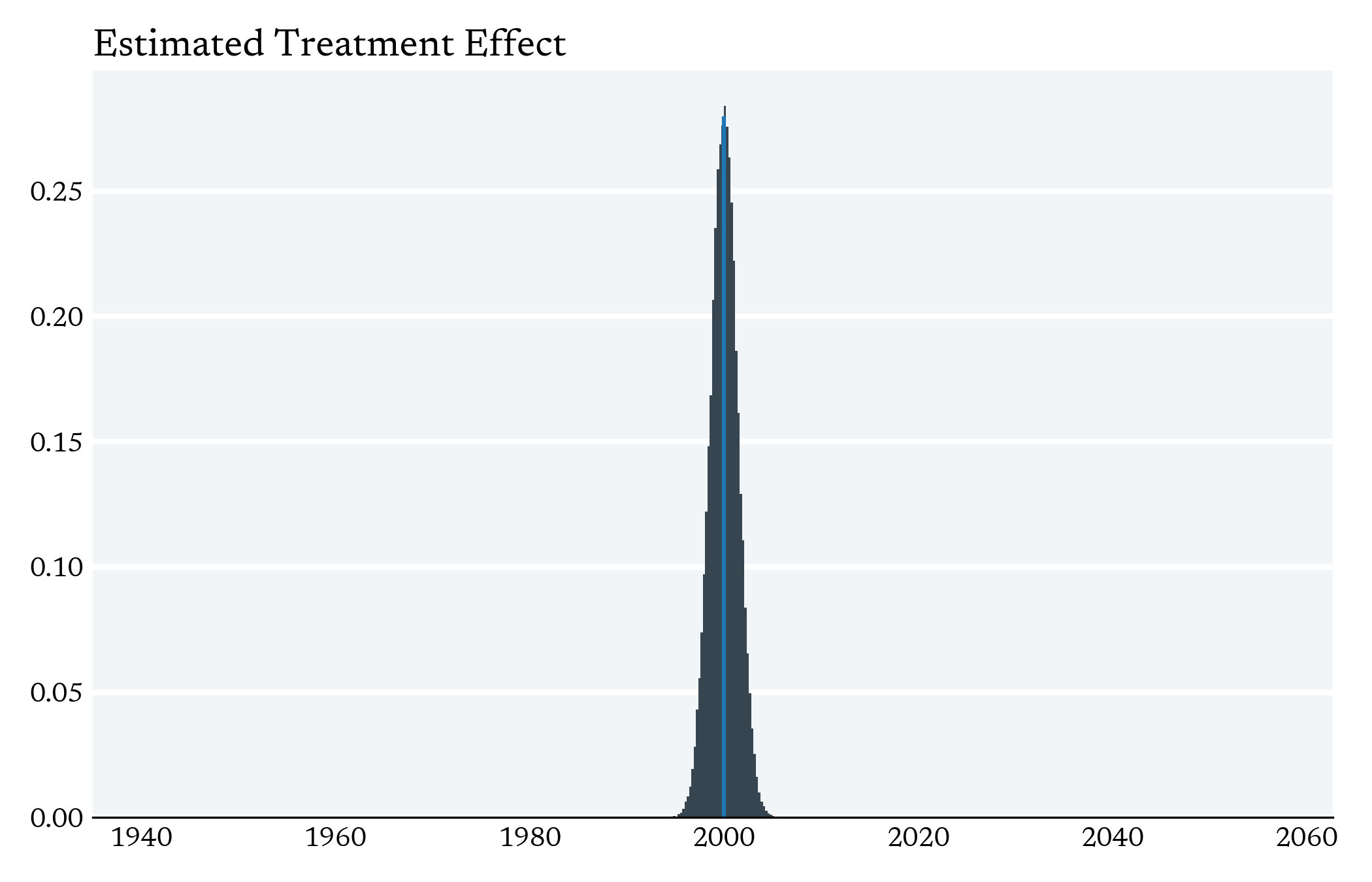
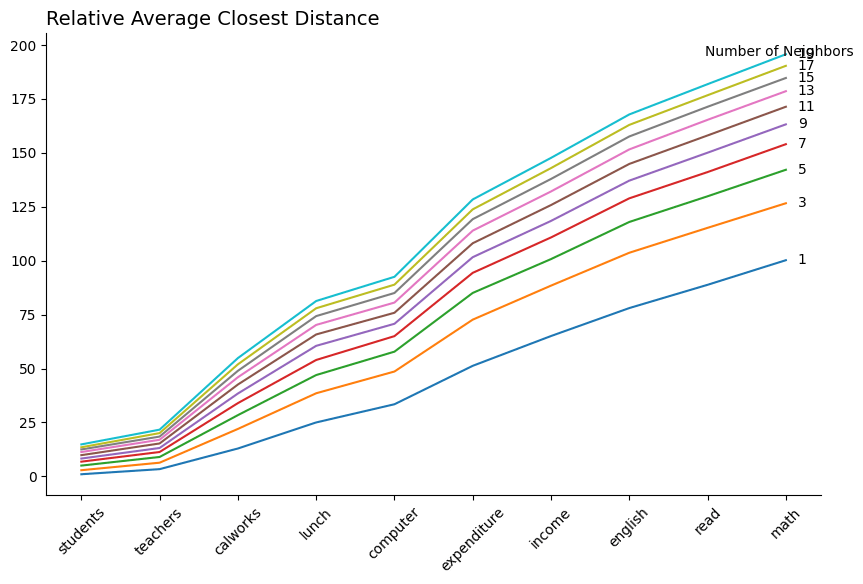
The curse of dimensionality

The Central Tension in Causal Inference is between local variation in Treatment and the Curse of Dimensionality

Linear Regression Models

Summary

In causal inference, we are concerned about selection bias

\mathbb{E}[\tilde{Y}_i(0) \vert D=1] - \mathbb{E}[\tilde{Y}_i(0) \vert D=0] \neq 0

One idea is to include additional controls such that

\mathbb{E}[\tilde{Y}_i(0) \vert D=1, X_i] - \mathbb{E}[\tilde{Y}_i(0) \vert D=0, X_i] = 0

The Conditional Expectation Function is central to our Framework for Estimating Causal Effects

\mathbb{E}[Y_i \vert D_i, X_i]

Conditional Expectation Function

\beta_0 + \beta_1D + \beta_2X

Population OLS Model

\hat{\beta}_0 + \hat{\beta}_1D + \hat{\beta}_2X

Sample OLS Model

In Class Excise

Hypothetically, let's say you wanted to estimate the impact that a specific teacher had on the average student's midterm grade. 

(B) If so, which controls would you include to reduce the selection bias?

\tilde{Y}_i(0)

Notation

\tilde{Y}_i(1)
D_i

Indicator of specific teacher

Midterm grade if they didn't have that teacher

Midterm grade if they did have that teacher

(A) Are you concerned about selection bias? 

Estimation Challenges

  • In higher dimensions (multiple independent variables), the observations are more spread out, which makes it hard to think of taking "local" differences between treated and control

Curse of Dimensionality

  • Often the variables that we would most like to control for to reduce selection bias -- maturity, ability, motivation -- don't appear in our data set

Omitted Variables

Sensitivity

We're concerned that a variable like Ability, X, is driving the selection bias

\begin{align*}Y_i &= \gamma_0 + \gamma_1D_i + \gamma_2 X_i + \eta_i\end{align*}

Coefficient of Interest

Not in Our Data Set

\begin{align*}Y_i &= \beta_0 + \beta_1 D_i + \varepsilon_i \end{align*}

Let's say that we observe the Outcome and Treatment variable

\beta_1 = \gamma_1 + \gamma_2\frac{\text{Cov}(D, X)}{\text{Var}(D)}

Observed Coefficient

Coefficient of Interest

The average change in the outcome given a per unit change in the latent variable, holding treatment constant

Nuisance Parameter

The slope parameter from regressing the Treatment on the Latent Variable

Practical Perspective

At a High Level, Causal Inference doesn't work as well as we might hope

  • The Gold Standard in Causal Inference is a Randomize Control Trial
  • Most questions cannot be addressed via a randomized control trial
  • Even questions that you may initially think can be addressed via an RCT cannot be addressed via an RCT

I don't think this is emphasized as much as it should be in introductory econometric classes (which makes sense partly, why demotive the class?!)

Chetty et al. (2016)

Example

Using only experimental variation, we cannot determine whether the use of experimental vouchers has a high long run impact (however measured) than the use of standard vouchers

Research

Credible

Important

Choice Set

What This Means:

(1) We'll have to make "Approximations"

  • We'll want to learn math (perhaps more than you may like!) to be able to evaluate and think through these approximations
  • This necessitates the need to move beyond learning just from data (need to learn from individuals with on the ground experience)

(2) The data alone doesn't provide a unique answer to our question

In practice, we often cannot provide guarantees for the performance of our approach under plausible assumptions