Causal Inference
Business Analytics
All BU Questrom Students
Y
D
Income 5 years post grad
Coding Class (1/0)
\mathbb{E}[Y \vert D]
Y
X
Sample Space
SET A
SET B
(Countable)
(Uncountable)
Y
\mathbb{E}[Y \vert X]
All U.S. Houses
Price
Price
Price
\varepsilon
=
+
Y_i = \mathbb{E}[Y \vert X=X_i] + \varepsilon_i
Price of House
Average Price Given Its Size
Error Term
Y_i = \beta_0 + \beta_1\text{Size}_i + \eta_i
Price of House
Slope
Error Term
Y-intercept
\{(Y_i, X_i)\}_{i=1}^n
Observed
f(\theta, X)
Build & Fit
\mathbb{E}[Y\vert X]
Interest
Setup
Learning From Data
(1) Data
(2) Function Space
Parameter Space
(3) Objective Function
(4) Solver
(Build & Fit)
\varepsilon_i
\eta_i
\hat{\eta}_i
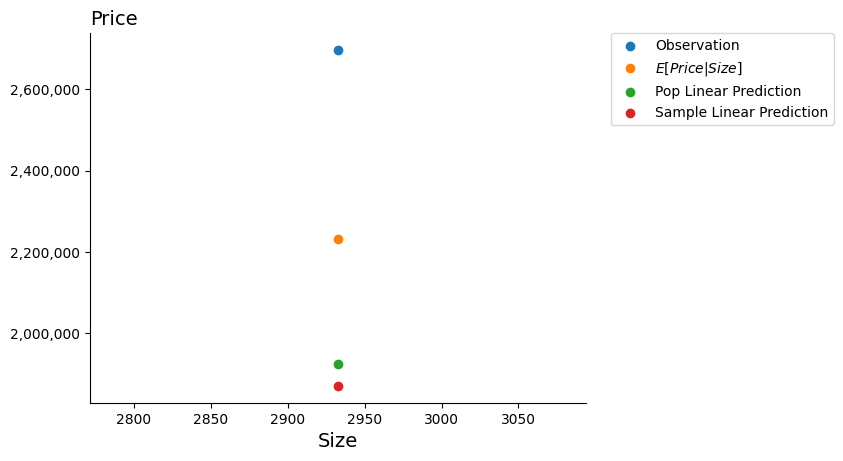
Y
X
All U.S. Houses
Price
Size
\mathbb{E}[Y \vert X]
1
\text{Var}(\bar{X}) = \frac{\text{Var}(X)}{n}
2
\frac{1}{n-1}\sum_{i=1}^n(X_i - \bar{X})^2 \approx \text{Var}(X)
3
\frac{1}{n(n-1)}\sum_{i=1}^n(X_i - \bar{X})^2 \approx \frac{\text{Var}(X)}{n}
\hat{\beta_1}= \hat{\gamma}_1 + \hat{\gamma}_2 * \frac{\text{Cov}(D_i, X_i)}{\text{Var}(D_i)}
Coefficient of Interest
(Single Variable Regression Model)
Coefficient of Interest
(Multivariate Regression Model)
Nuisance Parameter
(Multivariate Regression Model)
Slope Parameter from Regression Control on Treatment Variable