Chetty et al. (2016)

The economics of Housing & Homelessness

Big Picture Questions

How would you frame this paper?

"To some readers, it may seem odd that social scientists spent a decade or more, and millions of public and private research dollars, “proving” that high-risk neighborhoods are, in fact, bad for people. But that was not the aim. It was, instead, to examine, through careful tracking and comparison, what could happen if some people were given a chance to get out."

 - Moving to Opportunity : The Story of an American Experiment to Fight Ghetto Poverty

What mechanism would you like to have seen explored further?

School Access & Success

Role of transportation

Effects by family structure

What is an alternative identification strategy?

Y_i := \textrm{Children Income}_i
D_i := \textrm{Years in Low-Poverty Neighborhood}_i
Z_i := \textrm{Experimental Voucher}_i

What would scaling this experiment look like?

Motivation

\mathbb{E}[Y_i \vert \textrm{Low Poverty}] - \mathbb{E}[Y_i \vert \textrm{High Poverty}] >> 0

Motivation

Across Economic, Health, and Educational Outcomes

\mathbb{E}[\tilde{Y}(\textrm{Low Poverty})_i \vert \textrm{Low Poverty}] - \mathbb{E}[\tilde{Y}(\textrm{High Poverty})_i \vert \textrm{Low Poverty}]
+
\mathbb{E}[\tilde{Y}(\textrm{High Poverty})_i \vert \textrm{Low Poverty}] - \mathbb{E}[\tilde{Y}(\textrm{High Poverty})_i \vert \textrm{High Poverty}]

Motivation

Prior work based on MTO has shown that adults and older kids don't benefit economically from moving to lower poverty areas

Prior observational work  has shown that younger kids benefit economically from moving to lower poverty areas

Hypothesis

Economic Impact

Age at Move

Applied Econometrics

Identification Challenges

It can be difficult to compare the differences of the effects of vouchers across age-at move because ...

We're not able to condition on the year (2008-2012) and the age

1

We don't know how selection into the study might have differed by children's age

2

It's not entirely clear what the counterfactual trajectories are for these individuals (we see the poverty rate of the census tract declines for the control group too)

3

Averaging Across Sites

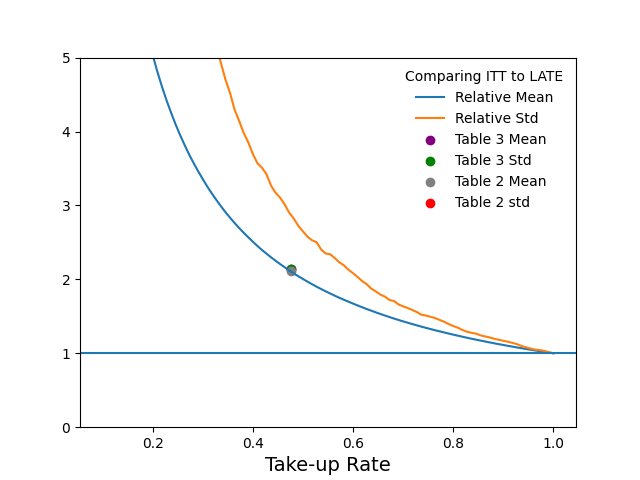
The LATE Effect is captured via:

Y_i = \beta\big(\mathbb{E}[D_i \vert X_i, Z] - \mathbb{E}[D_i \vert X_i] \big)

Is the linear regression with site fixed effects flexible enough to ensure that this term is nonnegative for those with Z=1 given that the complier groups can differ across sites?

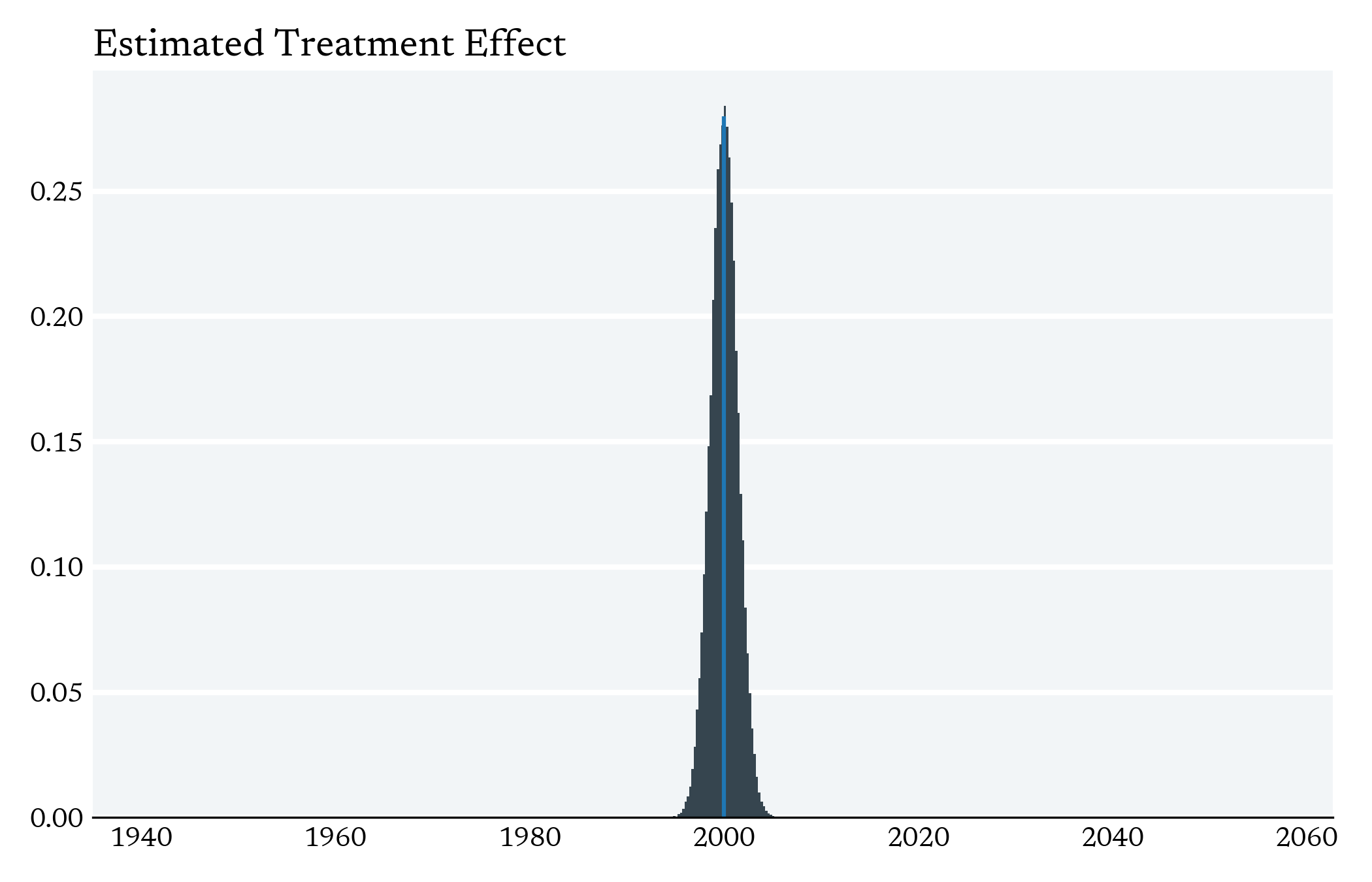
Standard Errors

Do the standard errors on the TOT look too small relative to the ITT?

Under the assumption of i.i.d data

\textrm{Var}\Big(\frac{1}{n}\sum y_i \Big) = \frac{1}{n^2}\Big(\sum \textrm{Var}(y_i) \Big)
= \frac{1}{n}\textrm{Var}\Big( y_i \Big)
\implies
= \frac{\sigma( y_i) }{\sqrt{n}}
\sigma\Big( \frac{1}{n} \sum y_i\Big)

Standard Errors

Under the assumption of i.i.d data

\textrm{Var}\Big(\frac{1}{n}\sum \frac{y_i}{c} \Big) = \frac{1}{c^2n^2}\Big(\sum \textrm{Var}(y_i) \Big)
= \frac{1}{c^2n}\textrm{Var}\Big( y_i \Big)
\implies
= \frac{\sigma( y_i) }{c\sqrt{n}}
\sigma\Big( \frac{1}{n} \sum \frac{y_i}{c}\Big)
\implies

If I divide the sample mean by 0.5

 I should double the standard error

 I should double the sample mean

Standard Errors

\textrm{Late} := \frac{\textrm{ITT} }{\textrm{Fstage} }

In practice, we're not dividing the ITT (a sample mean) by a constant. We're dividing it by the Fstage estimate which is a random variable

Details

Between 1994-1998 4604 families from Baltimore, Boston, Chicago, New York, and LA were randomly assigned into one of the following 3 groups

Treatment Assignment

Experimental Voucher

A housing voucher that could only be used in a census tract with poverty rate below 10% & Housing Mobility Consultation

Section-8 Voucher

A housing voucher

Control 

Retained access to public housing

After 1 year, experimental vouchers became Section 8 vouchers

Families had 4-6 months to lease an apartment and use their vouchers

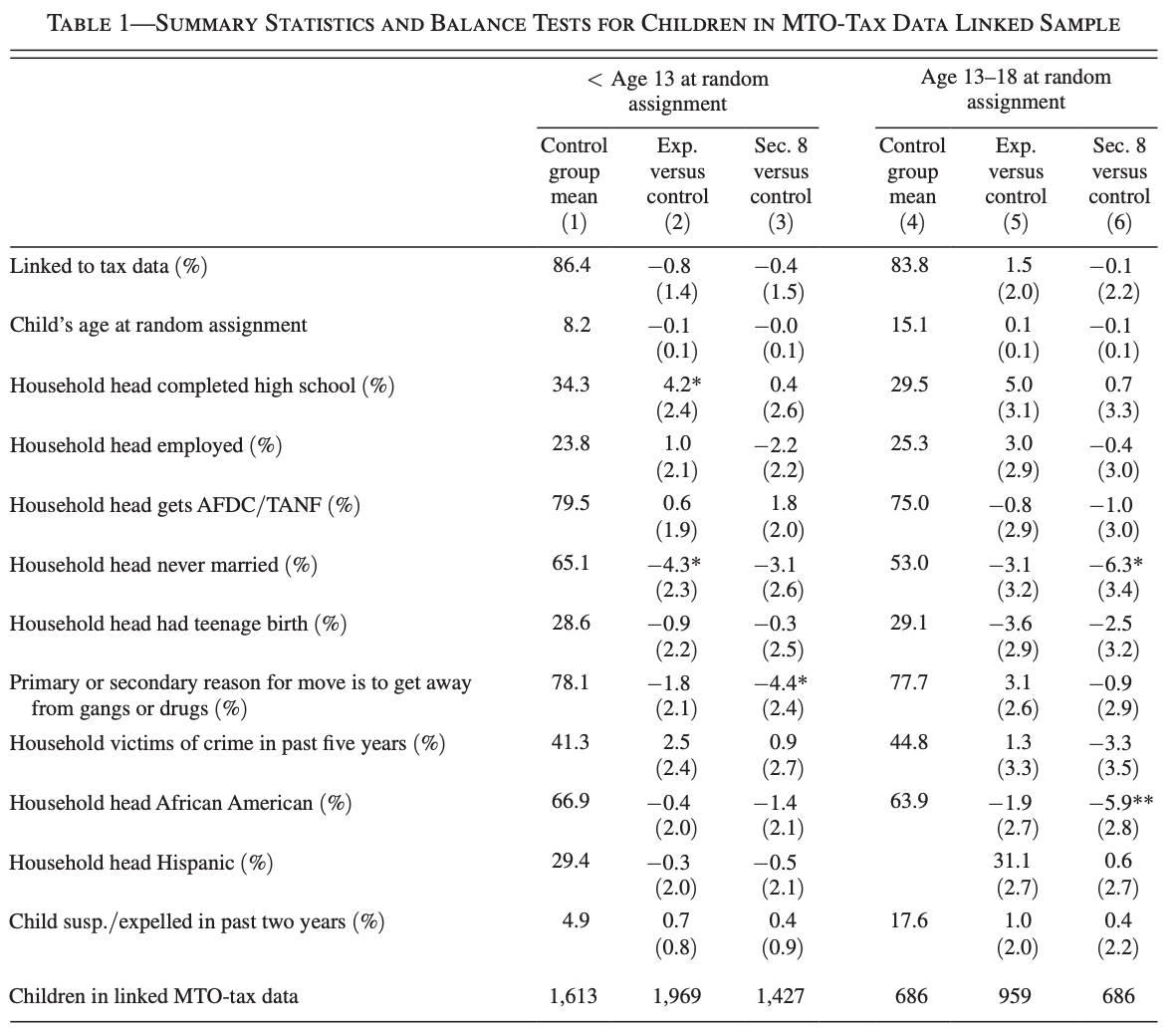
Check for Balance

Regression Models

Y_i = \alpha + \beta Z_i + \gamma X_i + \delta s_i + \varepsilon_i

Note this is a simplified version of the original regression

Intent-to-Treat

Y_i = \alpha + \beta \hat{D}_i + \gamma X_i + \delta s_i + \varepsilon_i

LATE

\approx \mathbb{E}_{X,S}\big[\mathbb{E}[Y \vert Z=1, X, S] - \mathbb{E}[Y \vert Z=0, X, S] \big]
\approx \mathbb{E}_{X,S}\big[\mathbb{E}[Y \vert D=1, X, S , \textrm{Complier}] \\ - \mathbb{E}[Y \vert D=0, X, S, \textrm{Complier}] \big]

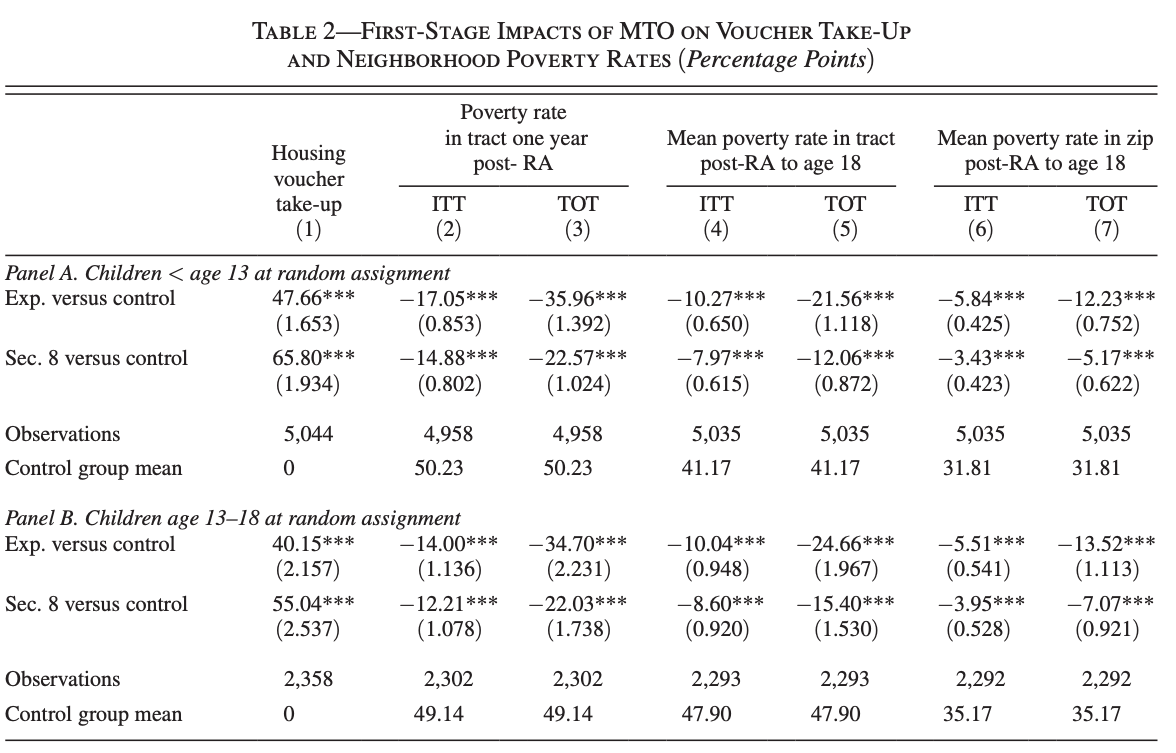
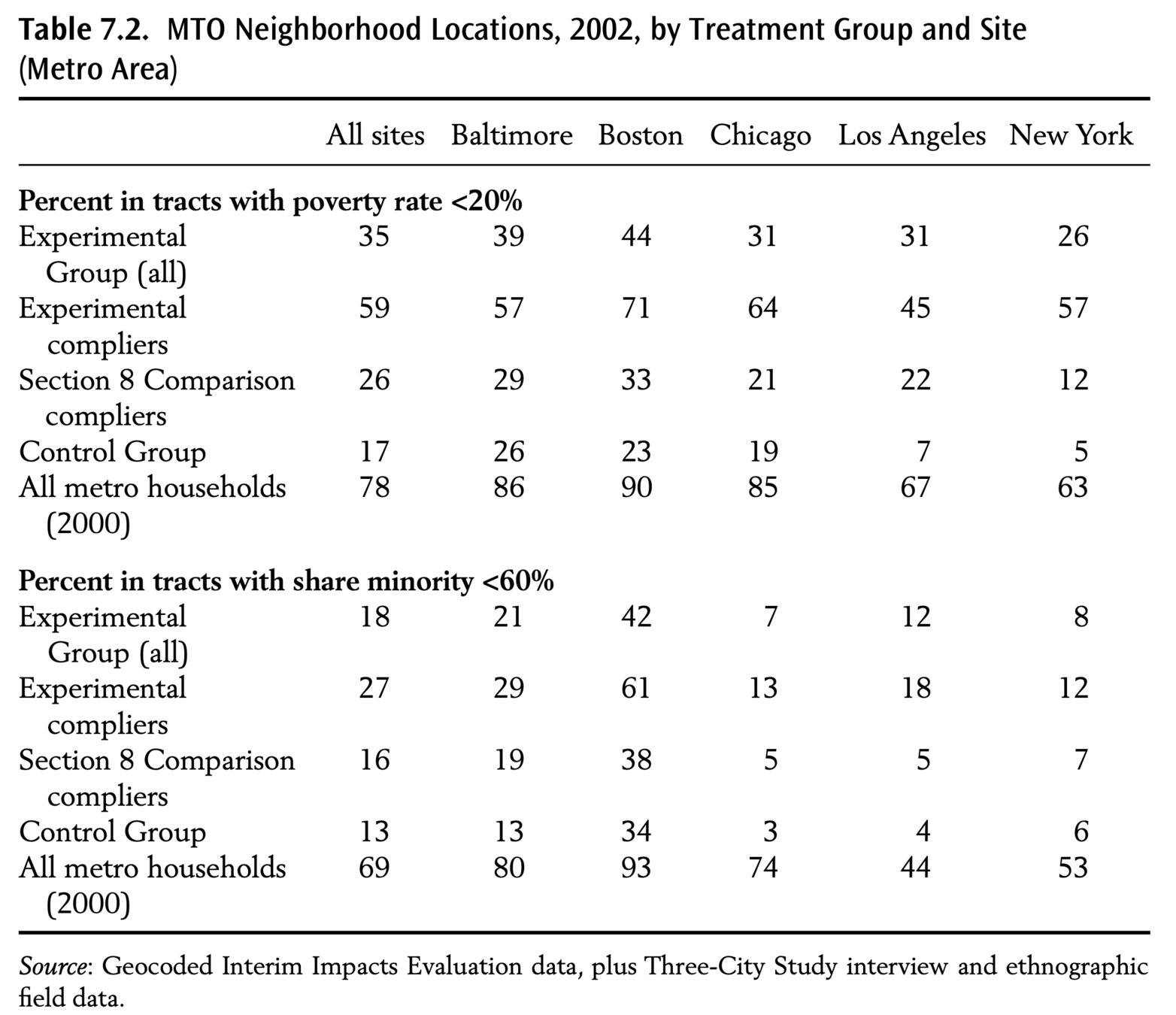
 "The mean control group family was living in a very distressed census tract one year after RA, with a 50 percent poverty rate—2.92 standard deviations (SD) above the national average in the 2000 census national tract-poverty distribution"

First Stage

Intent to Treat (Effect of Instrument on Outcome)

LATE (Effect of Treatment on Outcome for Compliers)

Why do the take-up rates differ based on the age of the child? (Families with older children are less likely to have a lease with a voucher)

Questions

What fraction of the control group eventually moves?

What's the typical distance of a move?

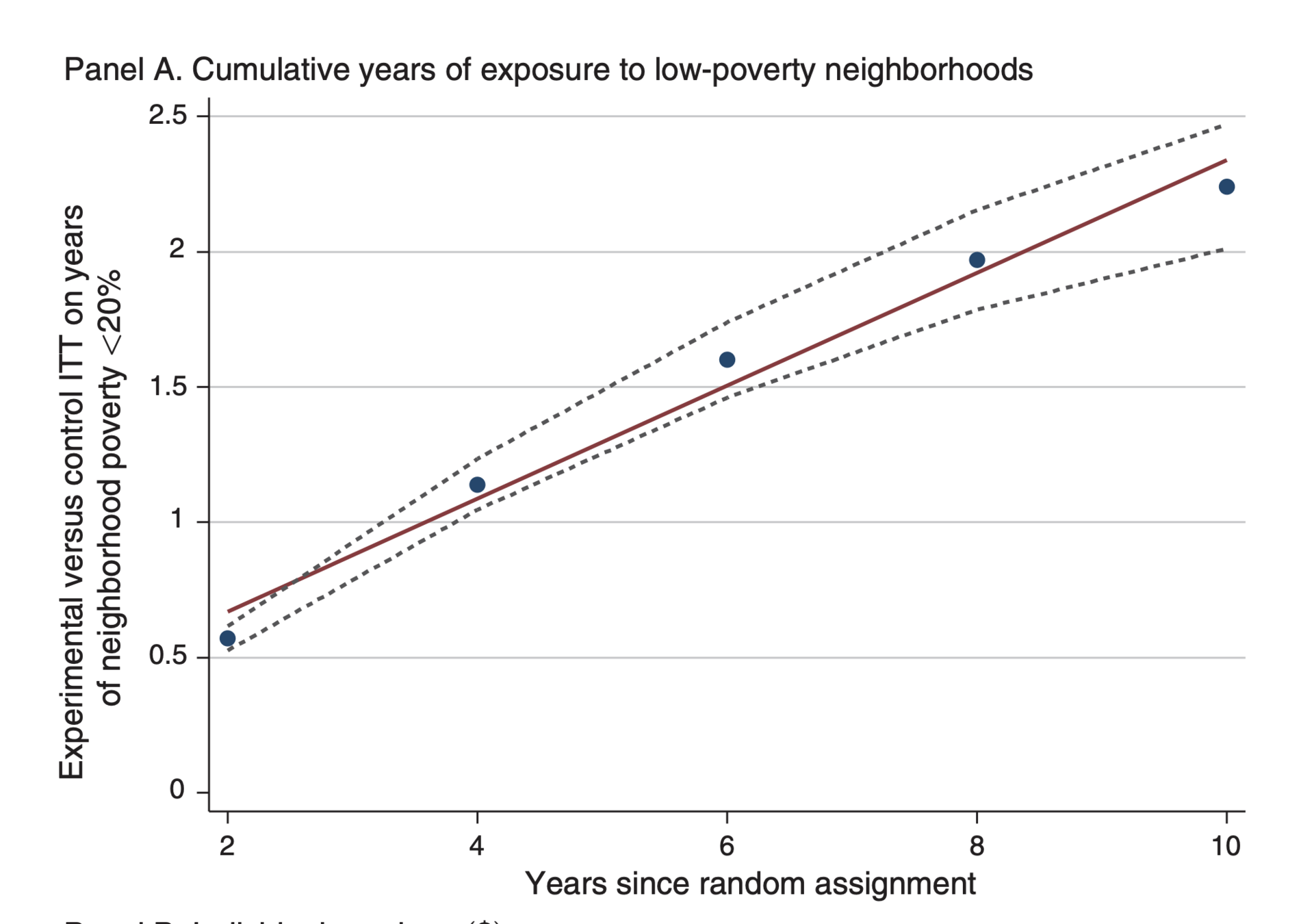
Effect of Experimental Voucher on Exposure to low-poverty

* Would be nice if the the axes had the same scale

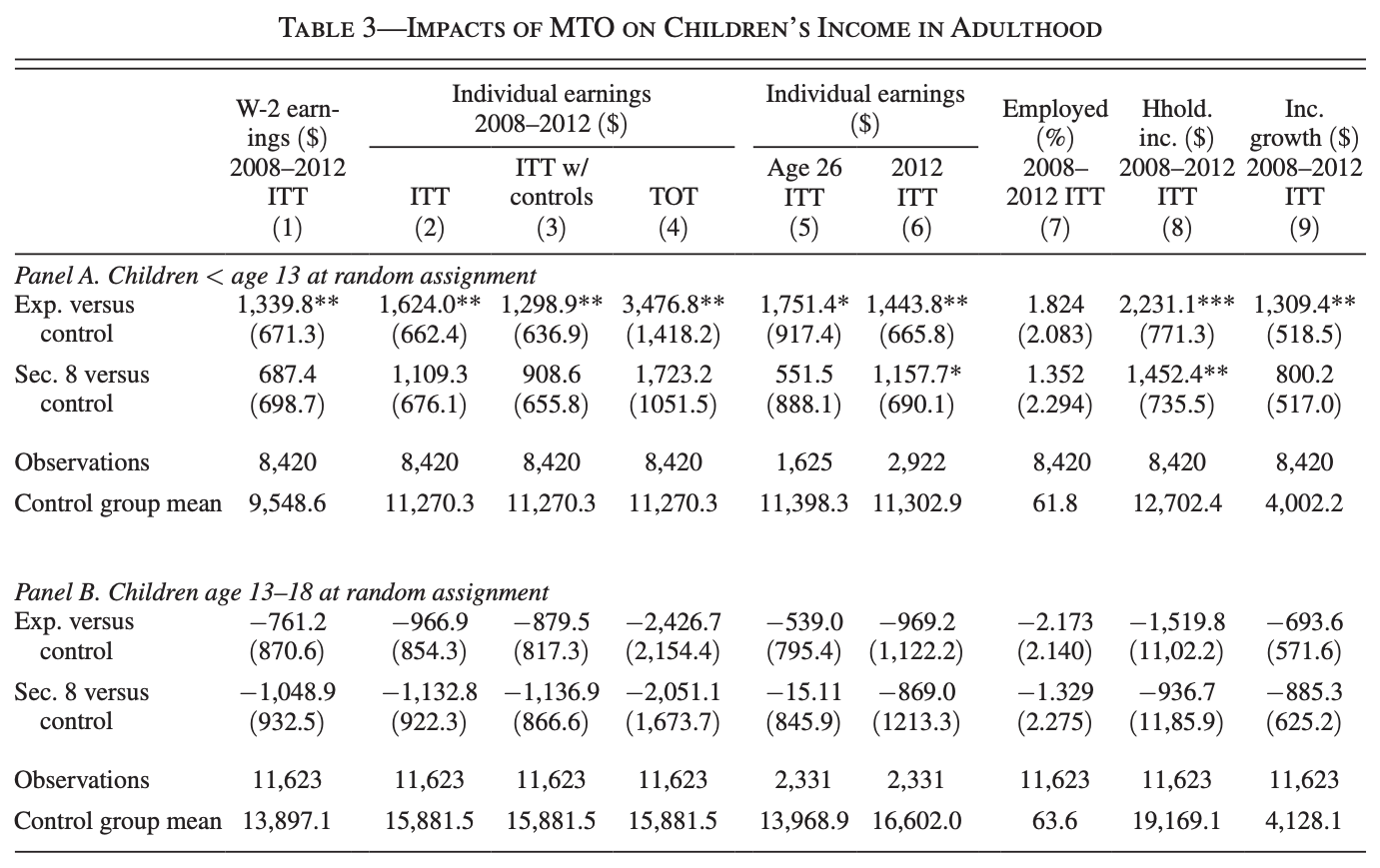
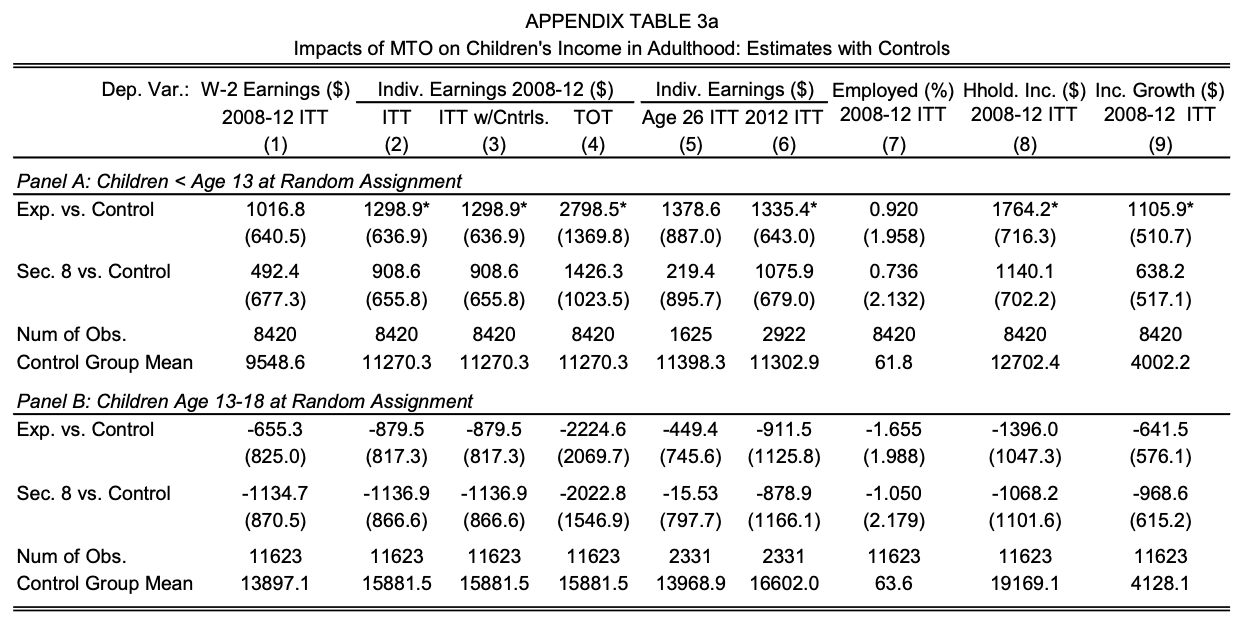
Questions

Why are regression results with controls the preferred specification?

Is the control employment mean surprisingly high?

Who is given greater weight without the controls

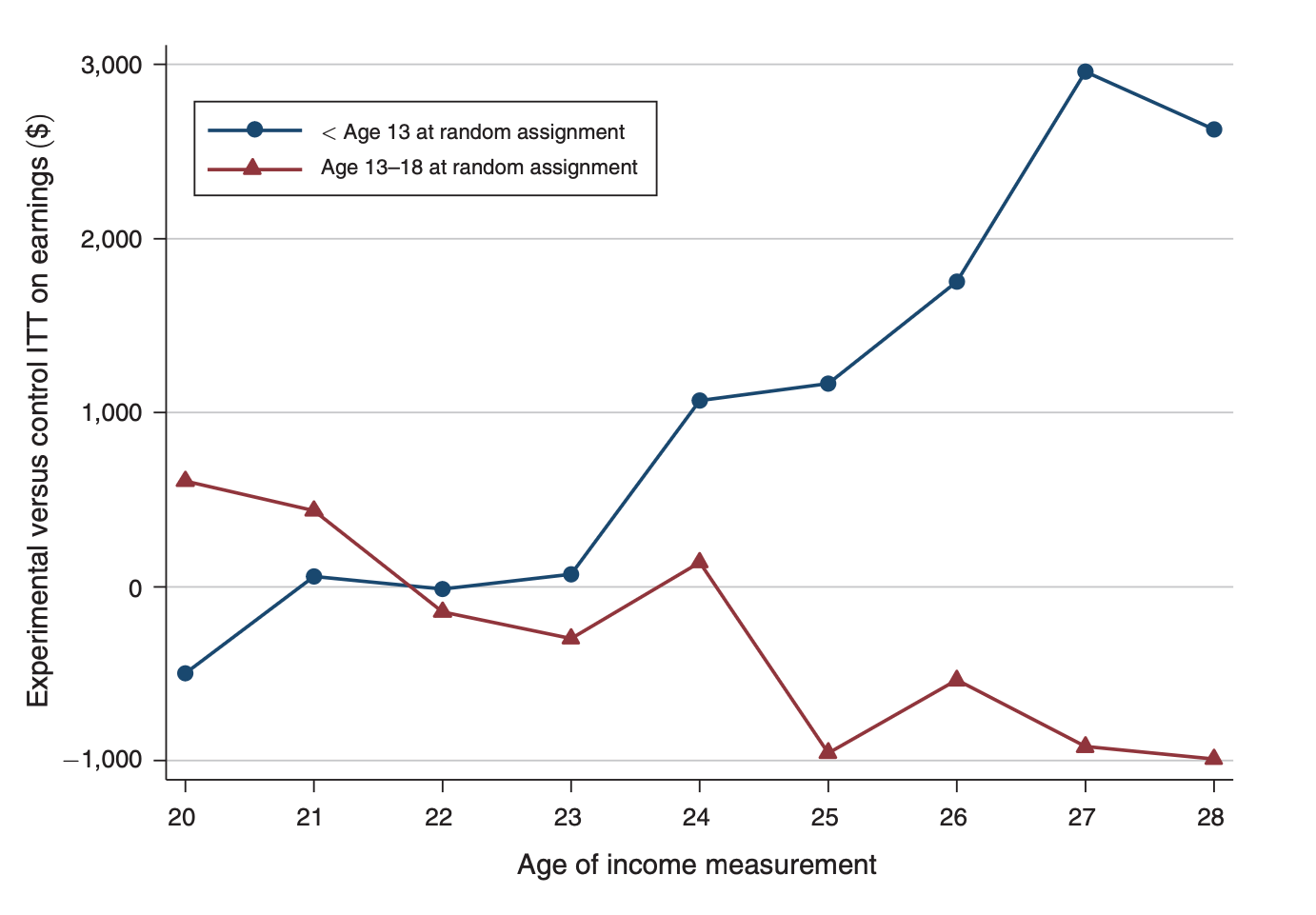
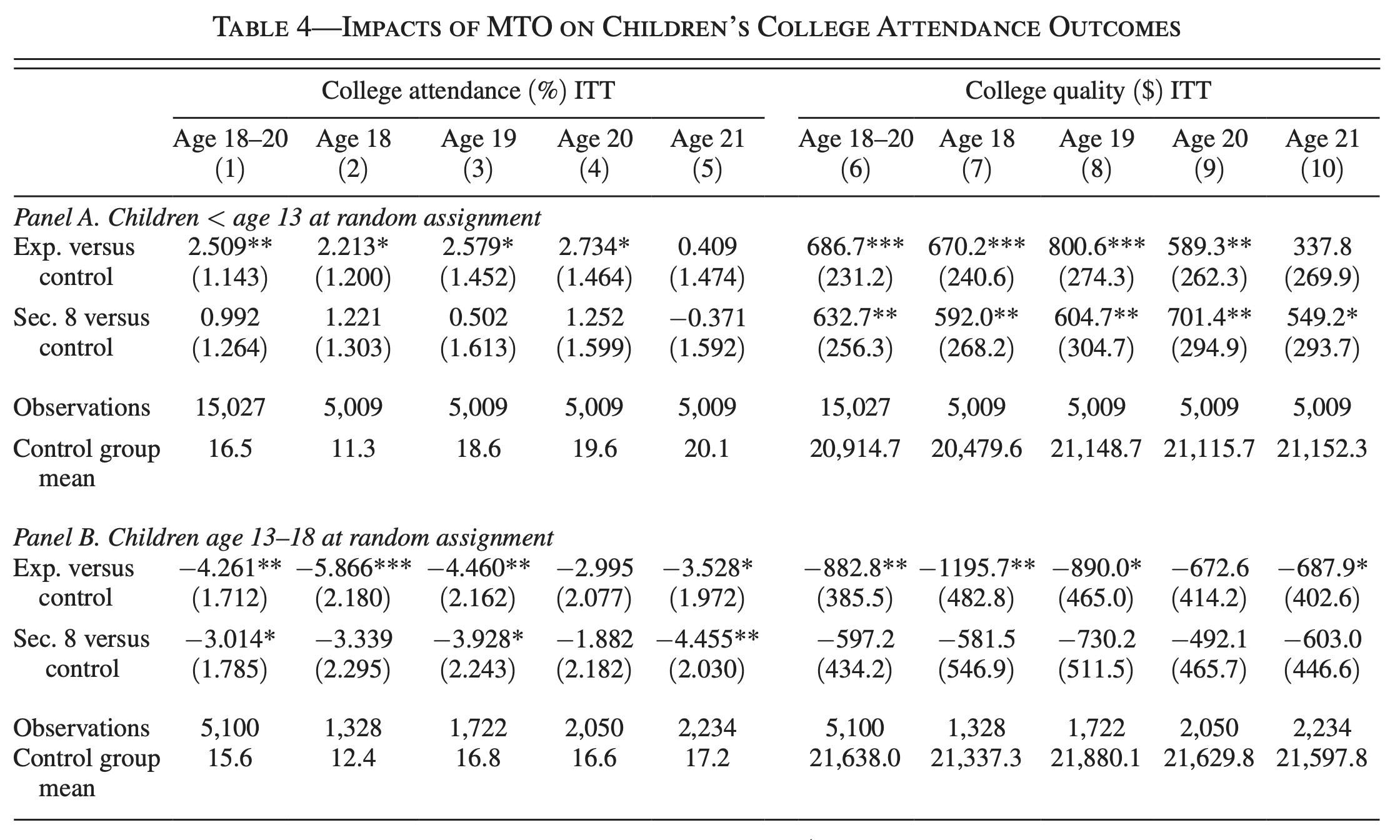
Comparing the control groups, we see that college attendance rate is lower in the older group

Is the impact on graduation lower than on attendance?

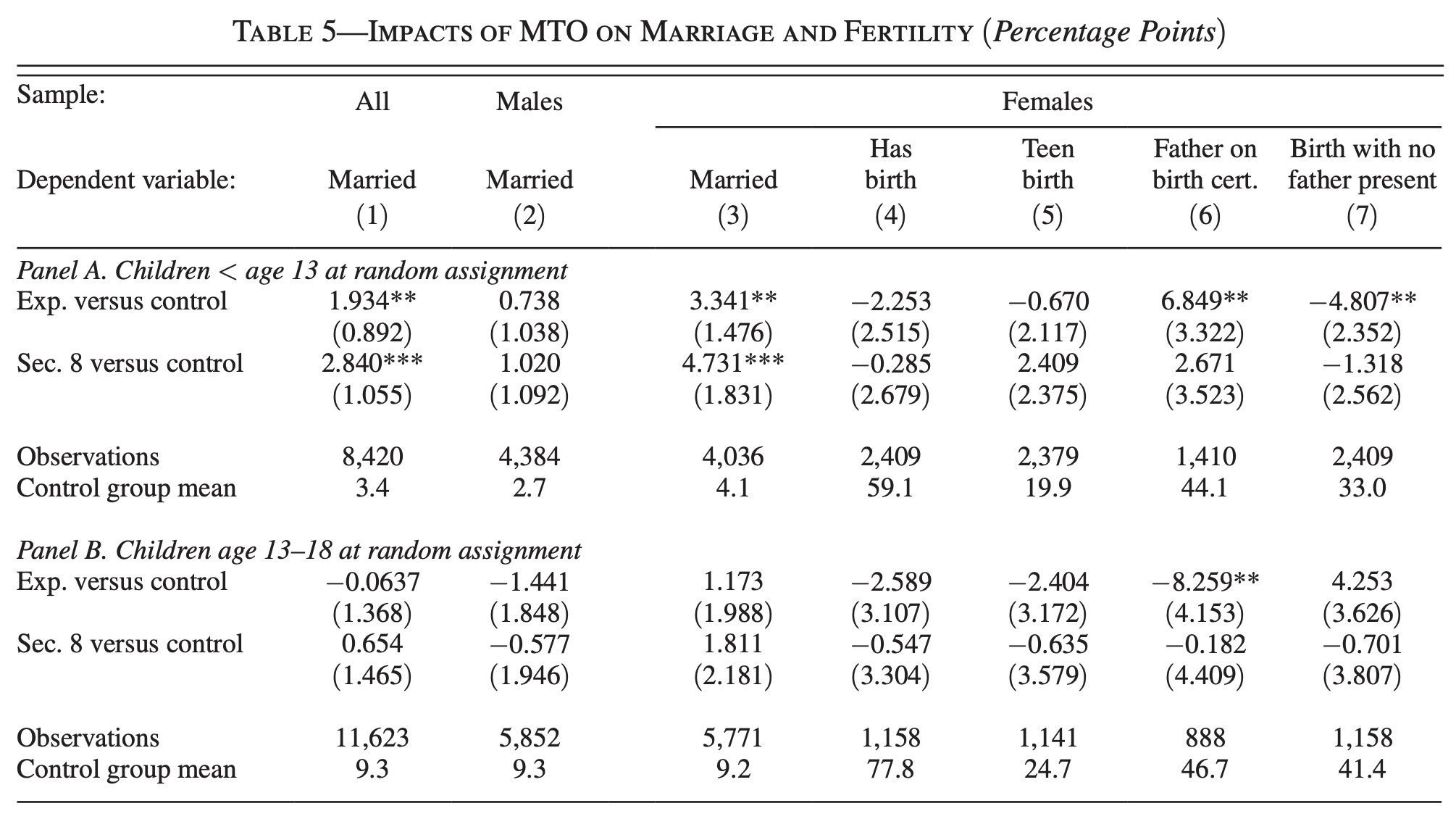
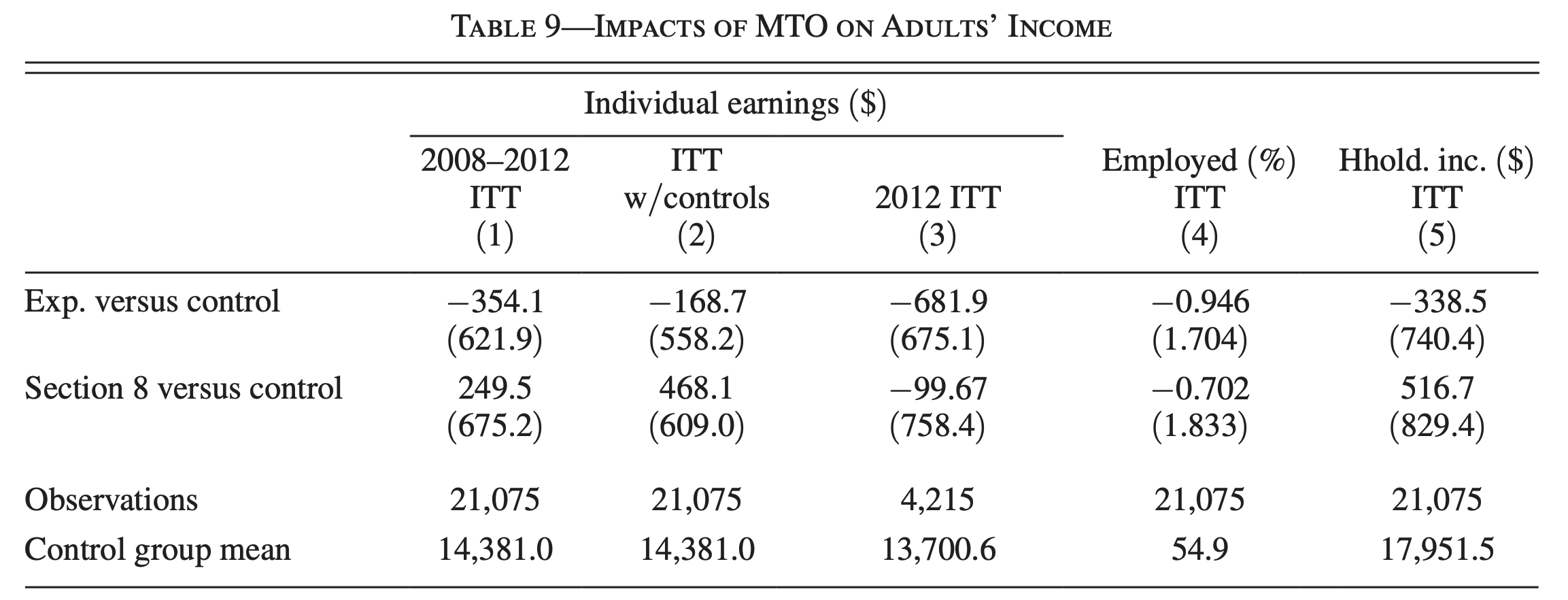
"all of the estimates are small and are not significantly different from zero"

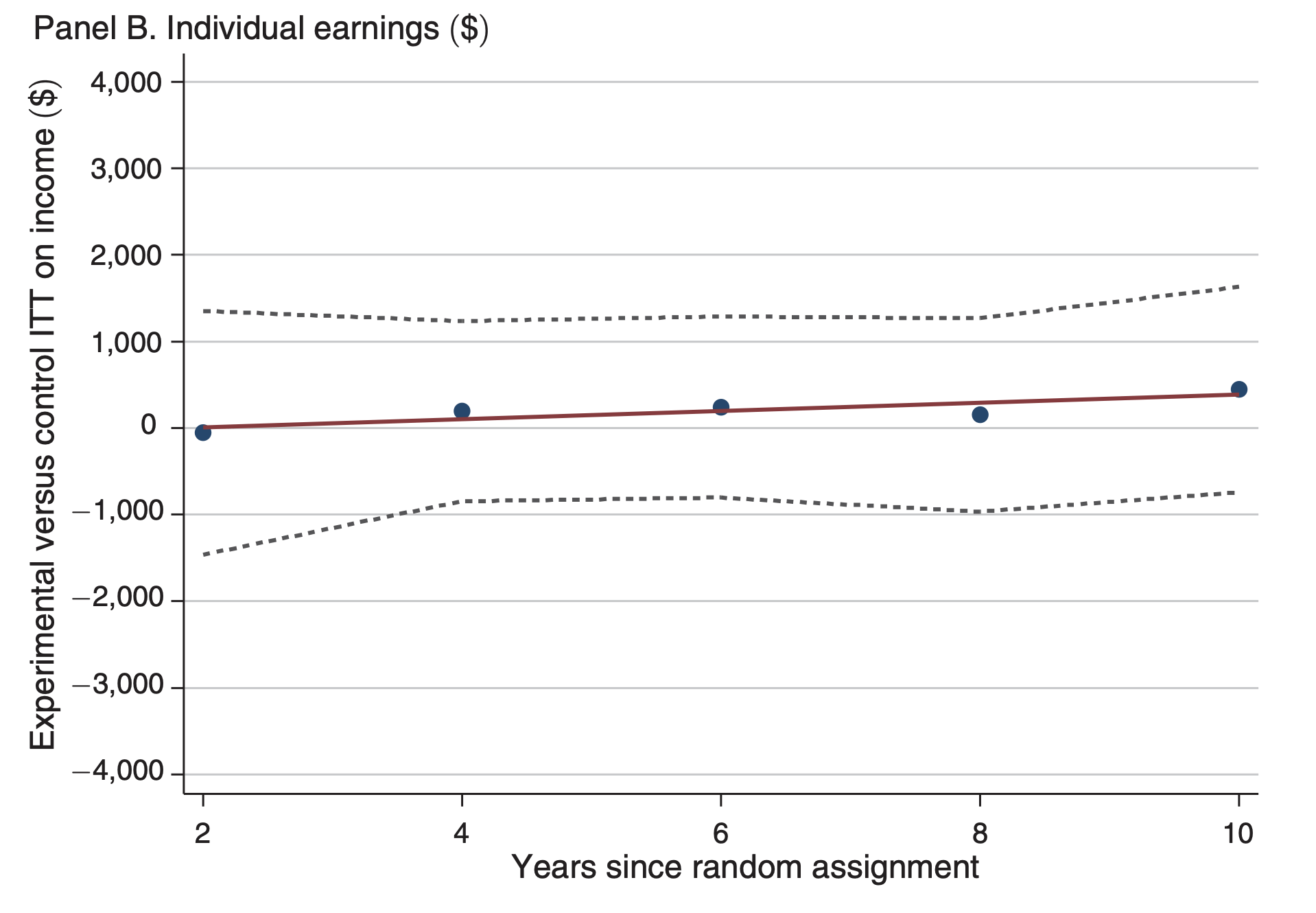
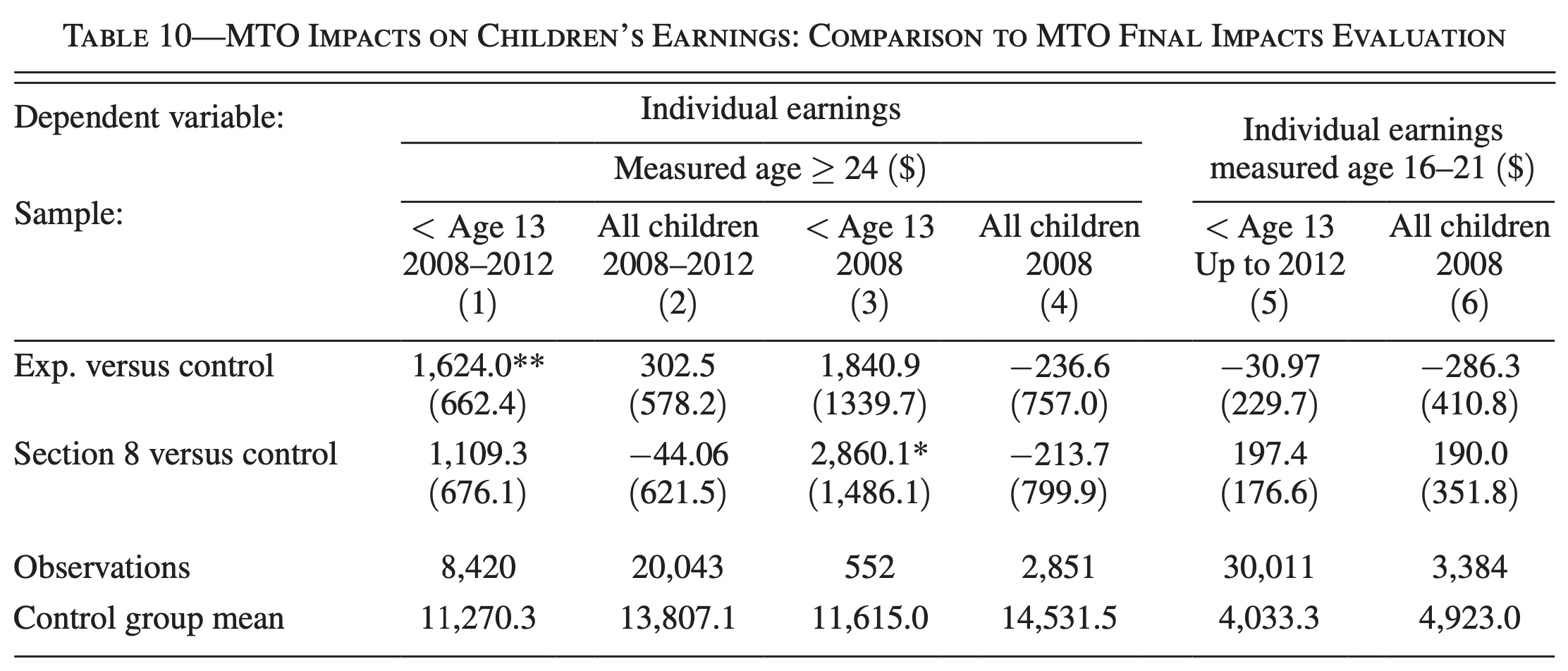
To do

Show that the ITT estimate can be expressed as the sample average

Add overview slide

Illustrate how text could be use to explain which observations receive greater weight without controls

1
2
3