Patrick Power

Regularizing the Forward pass

Shomik Ghosh

Overview

In many applied microeconomic settings, one can view their dataset as the realization of a stratified cluster randomized control trial

Locally, this makes it more likely that observations will be from the same cluster which can increase the variance of estimators that don't account for this

Treatment: Assigned at the Cluster Level

Controls: Vary at both the individuals and cluster level

We introduce an estimation framework that partials out the cluster effects in a nonparametric manner

Motivation

Research Designs: there is typically a tradeoff between more credible results and results that can better speak to the general equilibrium effects of a policy

Cluster Randomized Control Trials: offer a compromise between these competing aims

 Give up within cluster variation in order to achieve variation in density of the treatment.

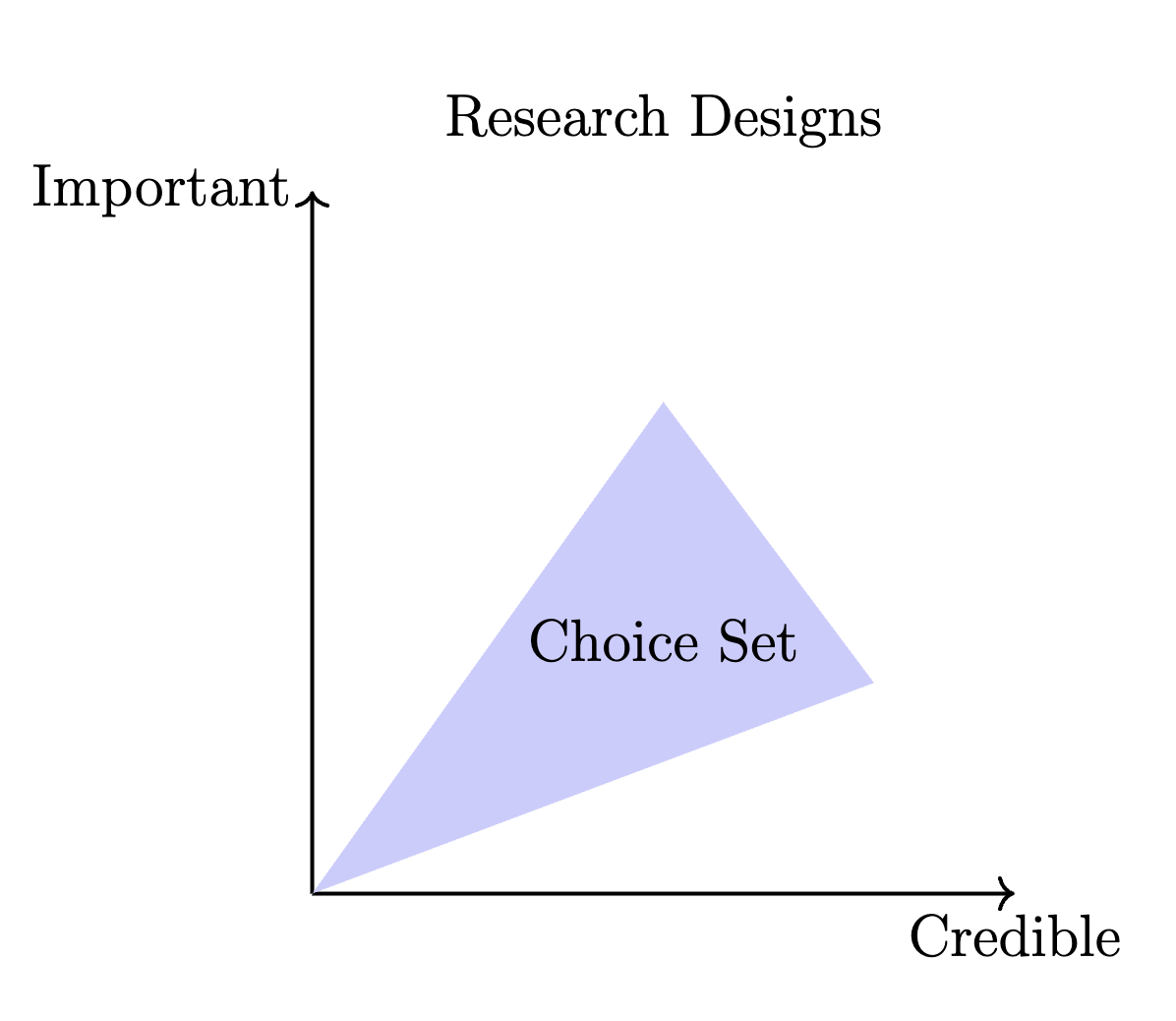
Motivation

In practice, the clusters which receive treatment are often not randomly selected

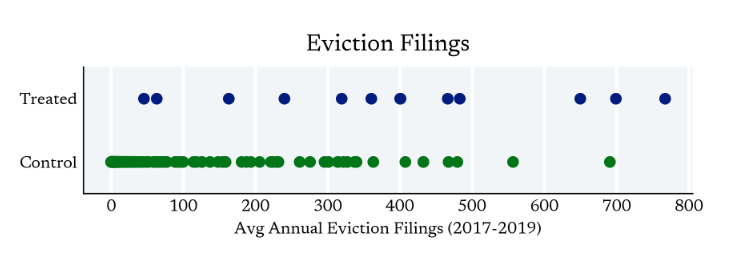
For identification purposes, we want to condition on cluster level features

Motivation

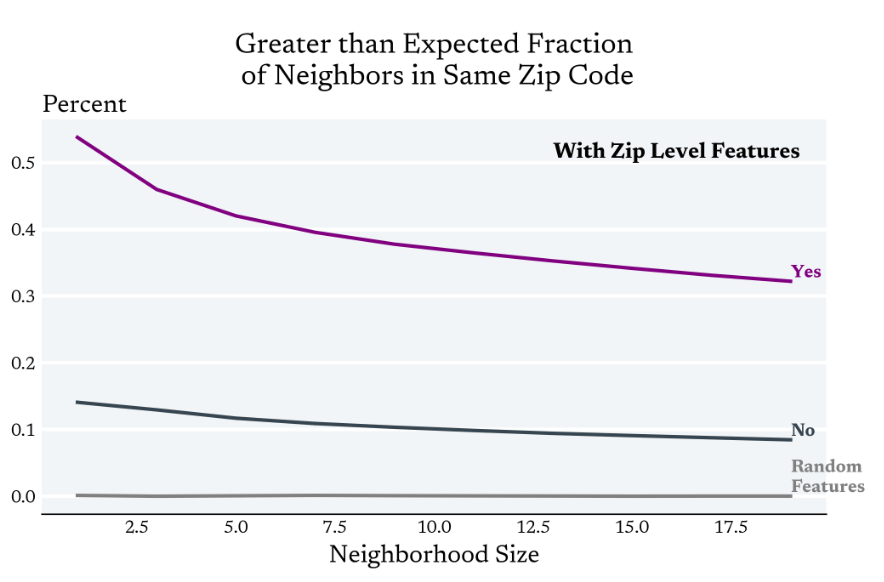
Clustered treatment assignment together with cluster level features makes it more likely that 'local' observations will be from the same cluster

Which can increase the variance 

of the estimator

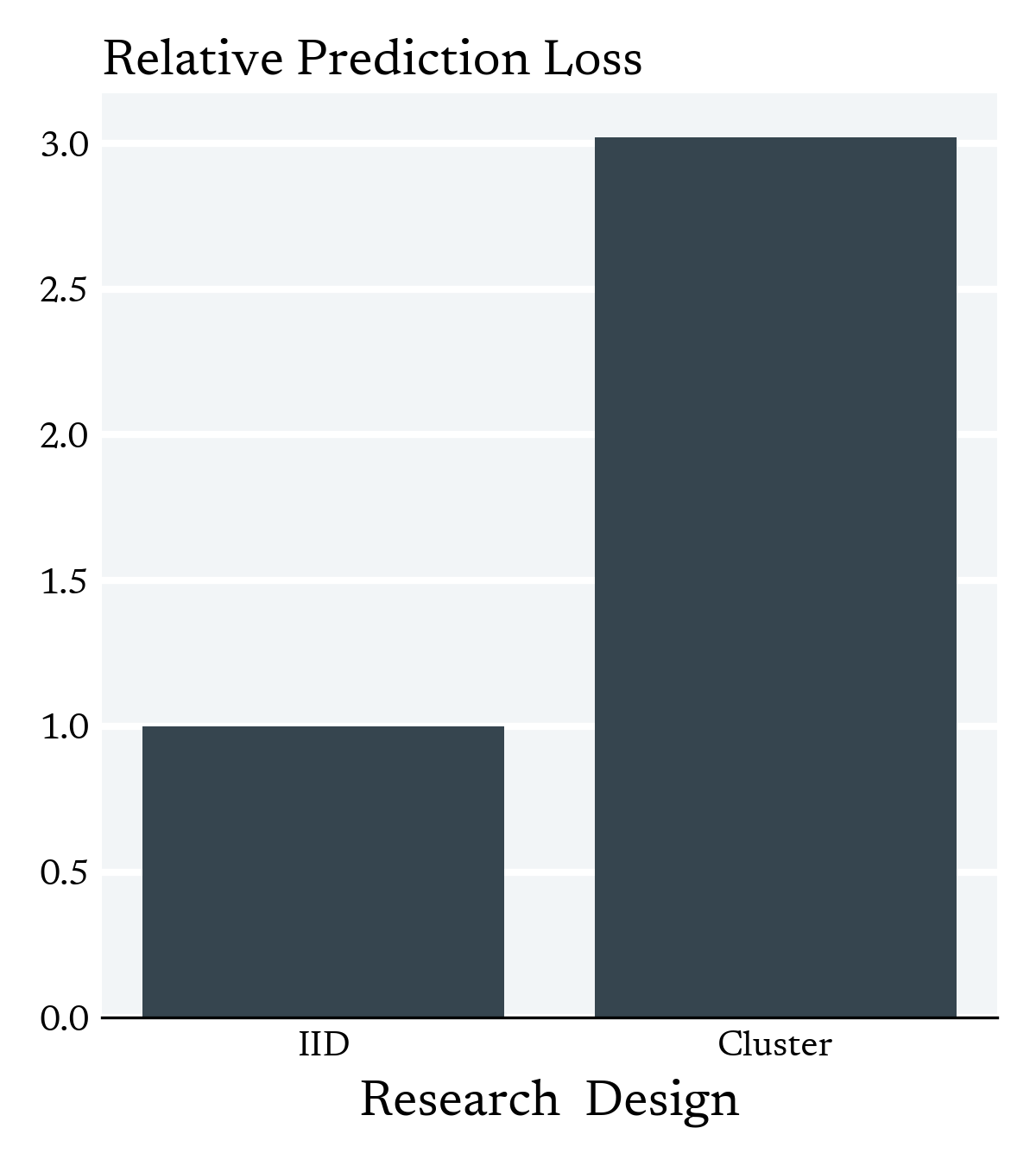
Challenge

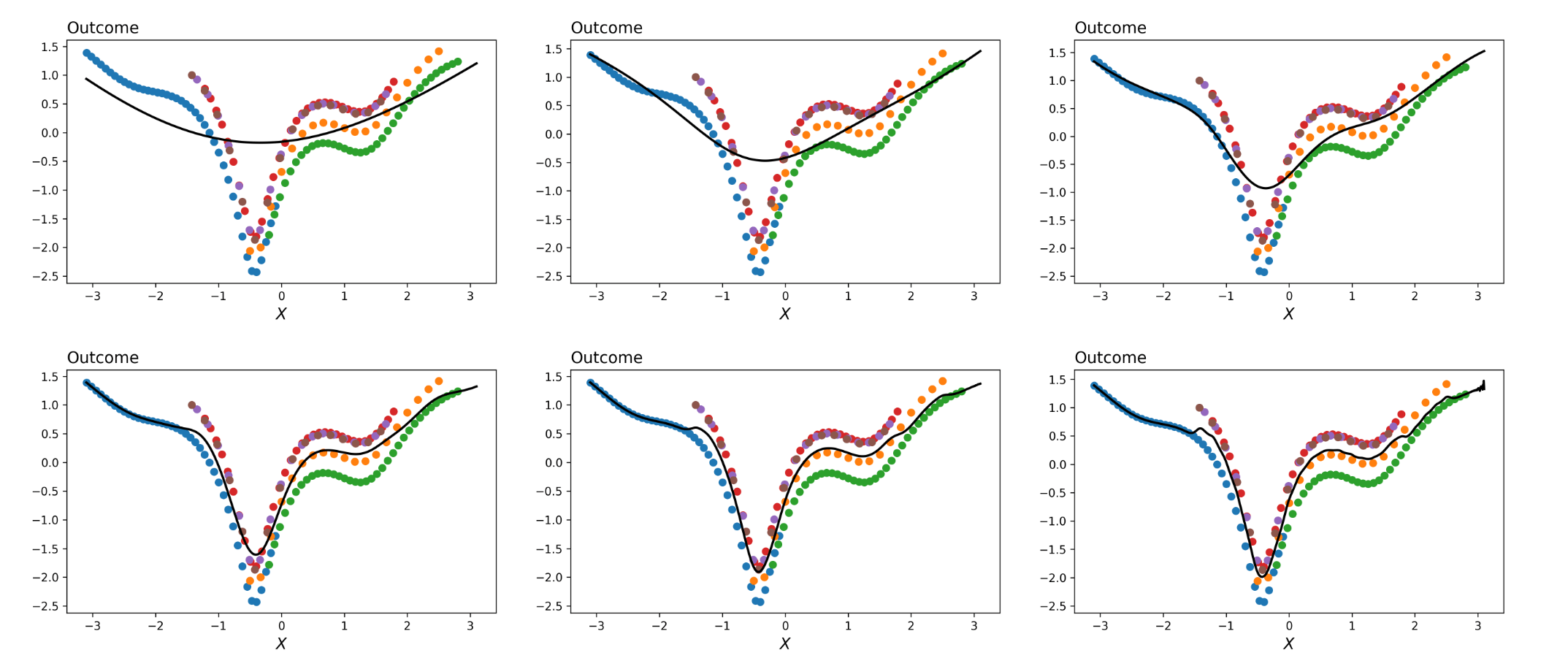
How do we locally correct for the presence of clusters in High Dimensions?

Challenge

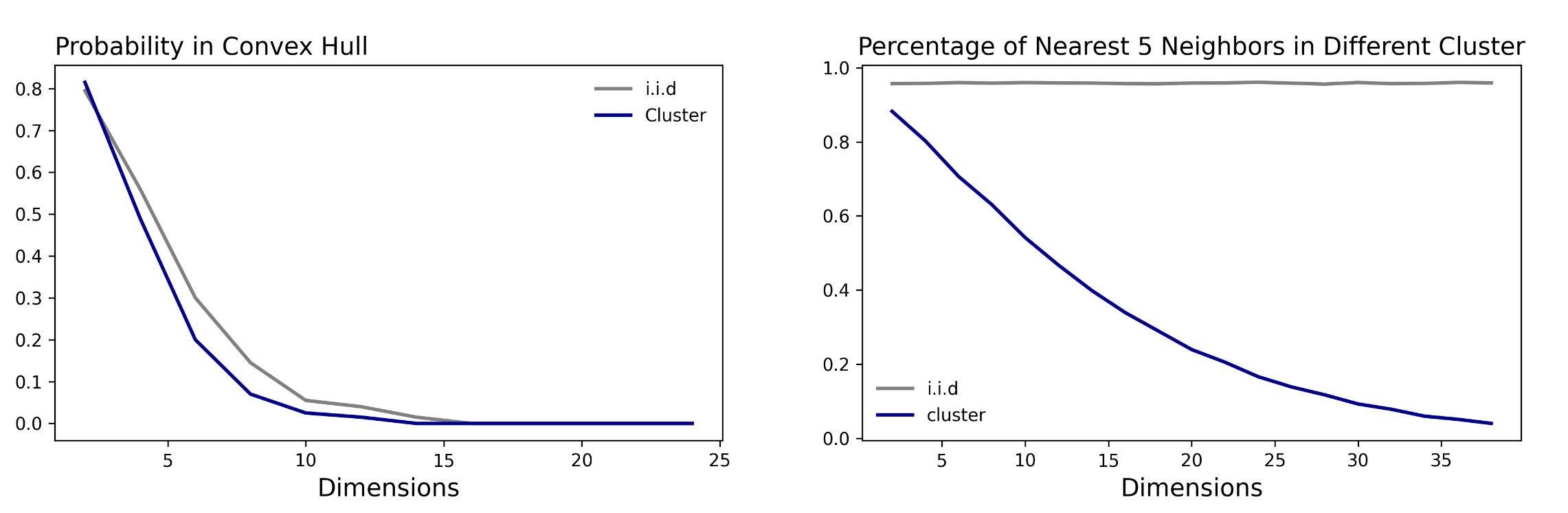
How do we rethink extrapolation?

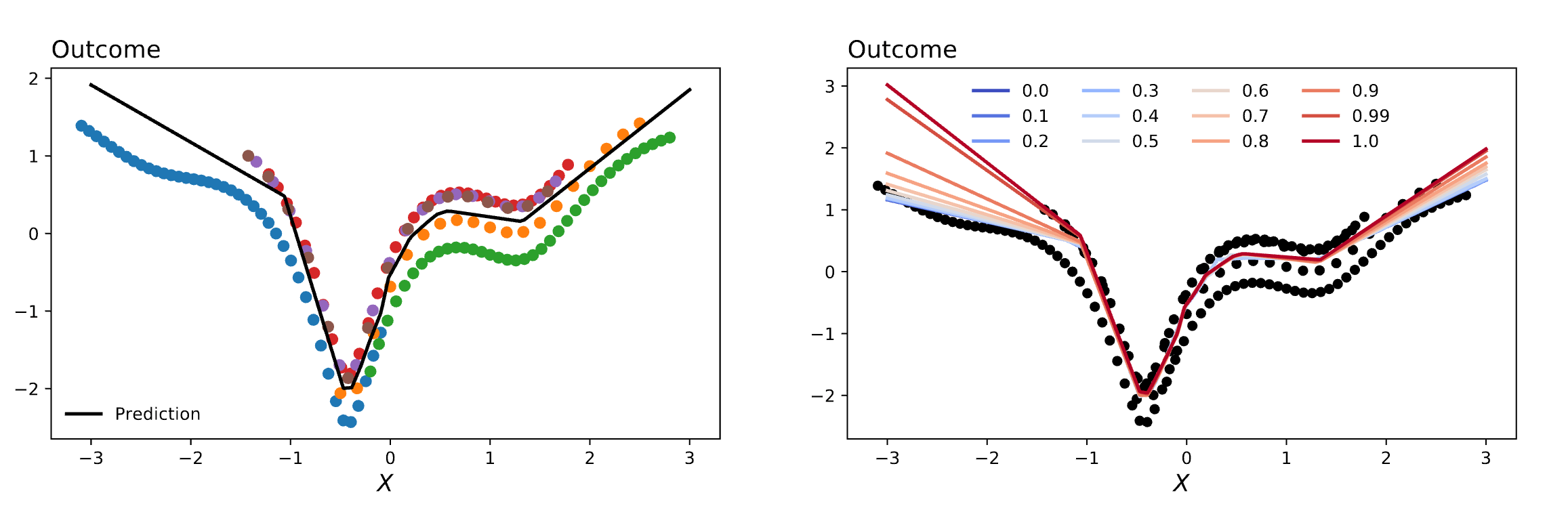
Regularizing the Forward Pass

\theta_c^k(\theta) := \theta^{k-1} - \alpha \nabla_{\theta}\frac{1}{n_c}\sum _{i \in c}L_i(\theta^{k-1}), \quad \theta^{0} = \theta

Model

L_i(\theta) := (y_i - f(\theta, x_i))^2
R_k(\theta) := \frac{1}{N}\sum _{i} \alpha L_i(\theta) + (1-\alpha) L_i(\theta_{c}^k(\theta) \\
\theta_c^k(\theta) := \theta^{k-1} - \alpha \nabla_{\theta}\frac{1}{n_c}\sum _{i \in c}L_i(\theta^{k-1}), \quad \theta^{0} = \theta

Model

L_i(\theta) := (y_i - f(\theta, x_i))^2
R_k(\theta) := \frac{1}{N}\sum _{i} \alpha L_i(\theta) + (1-\alpha) L_i(\theta_{c}^k(\theta) \\

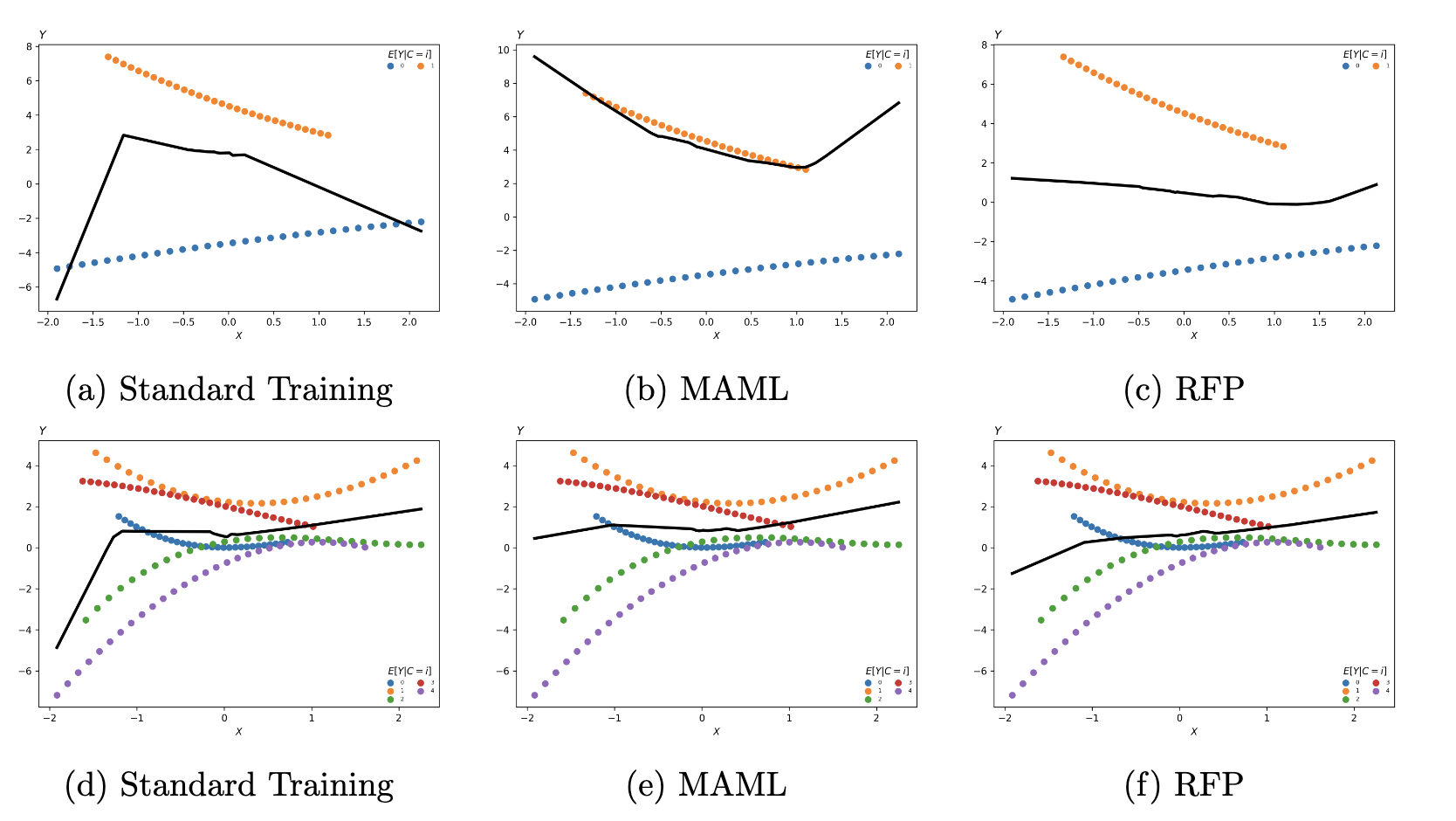
Simulations

LLMS

Because we partial out the cluster effects via bi-level gradient descent, the same procedure can be applied to LLMs

def process_text(batch):
    tokens = tokenizer(batch, return_tensors="jax", padding=True)
    tokens = {key: jnp.array(v) for key, v in tokens.items()}
    return tokens

It's as simple as "batching" the inputs

def cluster_process_text(c, n, batch):
    tokens = process_text(batch)
    tokens = {'input_ids': tokens['input_ids'].reshape(c, n, -1),
              'token_type_ids': tokens['token_type_ids'].reshape(c, n, -1),
              'attention_mask': tokens['attention_mask'].reshape(c, n, -1)}
    return tokens
+