Accurate identification of basins of attraction in jammed and glassy systems
Praharsh Suryadevara
Mathias Casiulis
Stefano Martiniani


Understanding Energy Landscapes
Energy as a function of conformational angles of a molecule
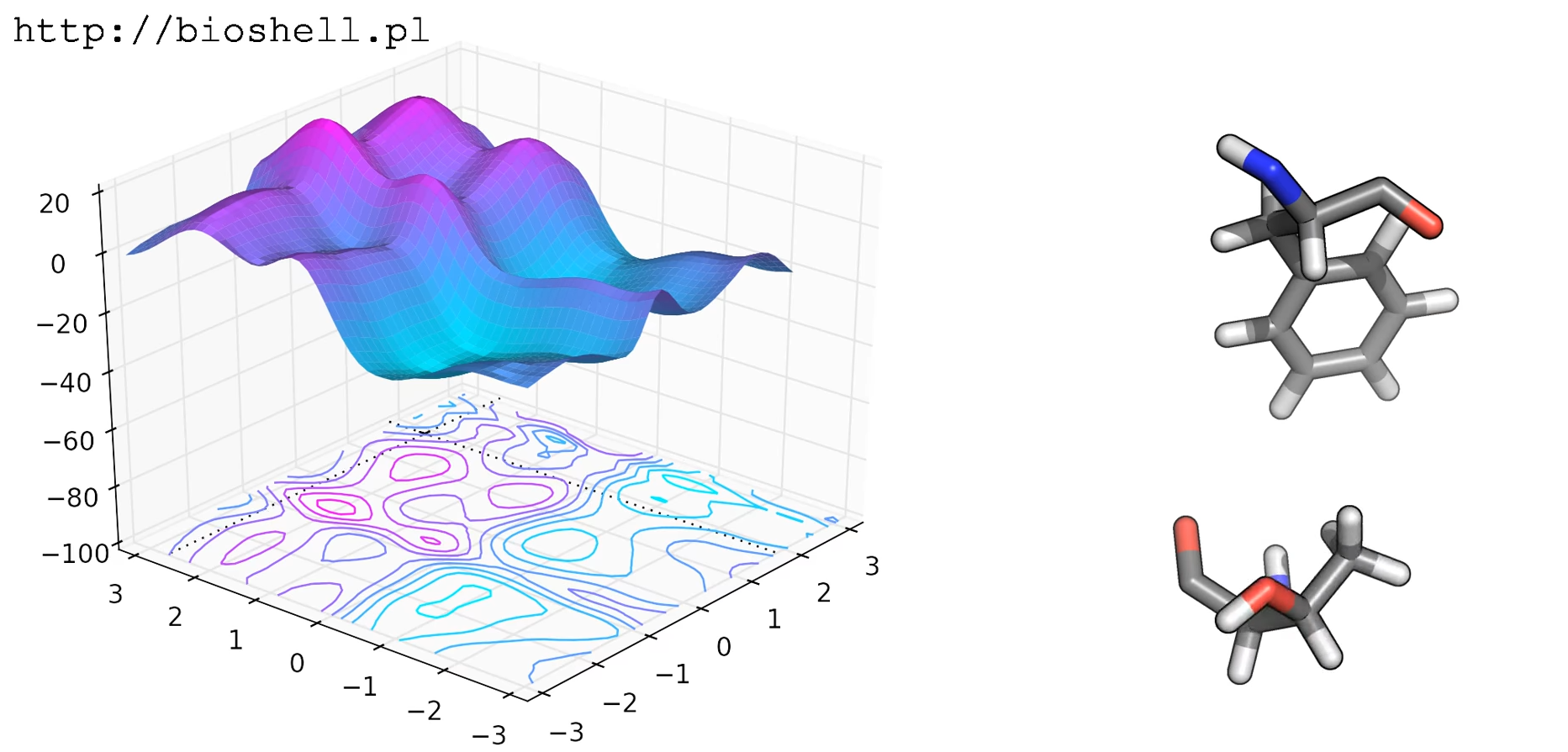
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
\(x_0\)
\(x_{min}\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
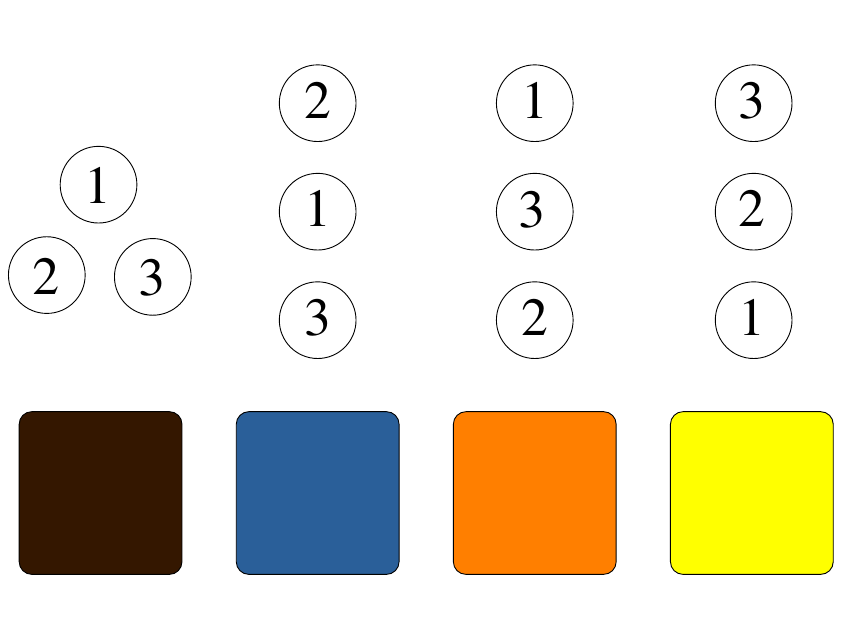
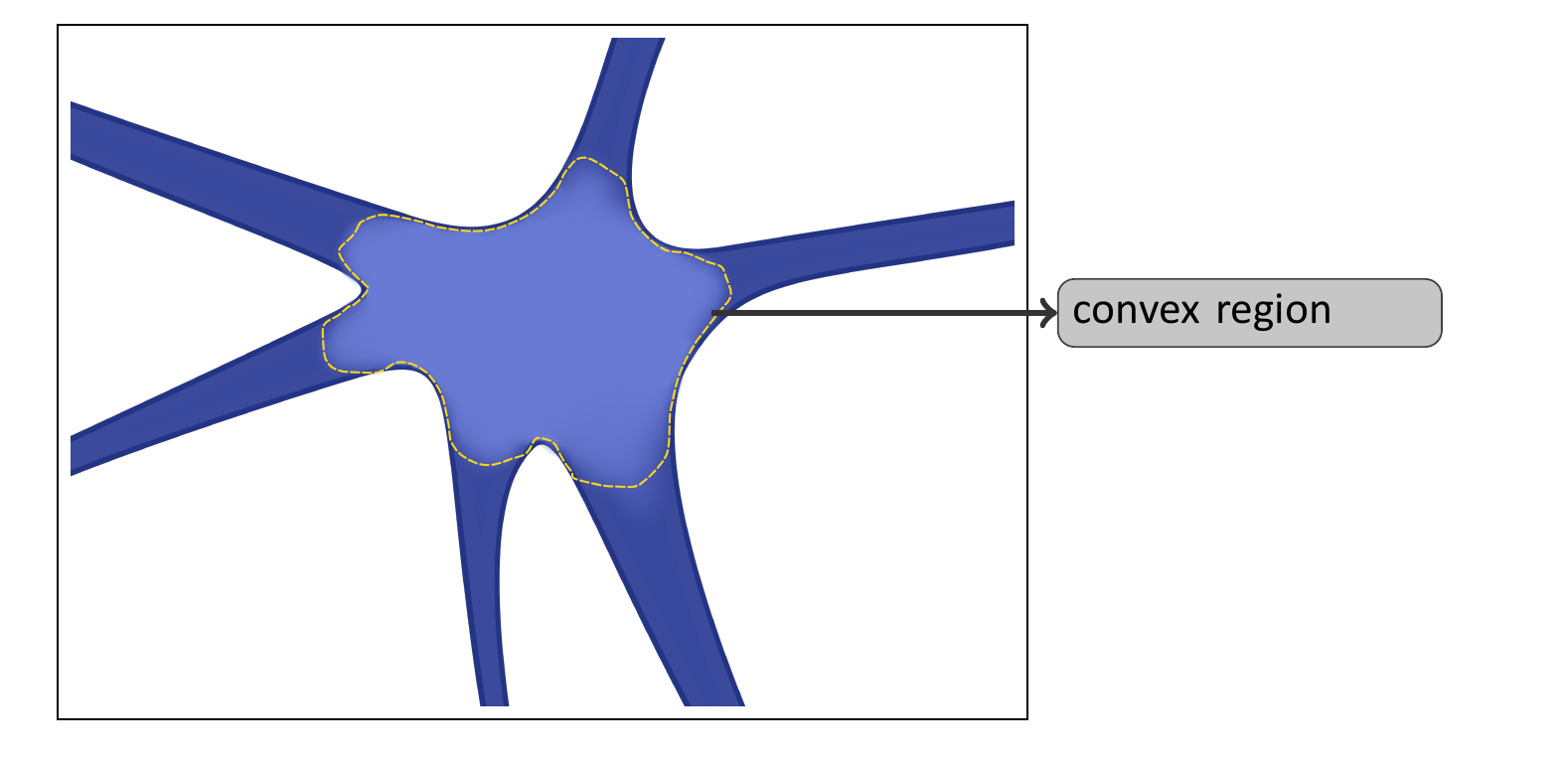
basin 2
Basin tiling (what we're interested in)
basin 1
basin 3
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
Steepest Descent
Systems
Bidisperse Hertzian soft spheres
$$ V_{ij}(r) =\begin{cases} \frac{\epsilon}{p} \left( 1 - \frac{r}{r_{i} + r_{j}} \right) ^{p} & r < r_{i} + r_{j} \\ 0 & r > r_{i} + r_{j}\end{cases}$$ with \(p\) = 2.5 and packing fraction \(\phi=0.9\)
Lennard Jones
$$ V_{ij}(r) = \epsilon \left( \left( \frac{\sigma}{r} \right) ^{12} - \left( \frac{\sigma}{r} \right)^{6} \right) $$
with \(\epsilon=1\) and \(\sigma=1\)

landscape dimension \(d_l \sim (N\times d)\)
Slicing the energy landscape

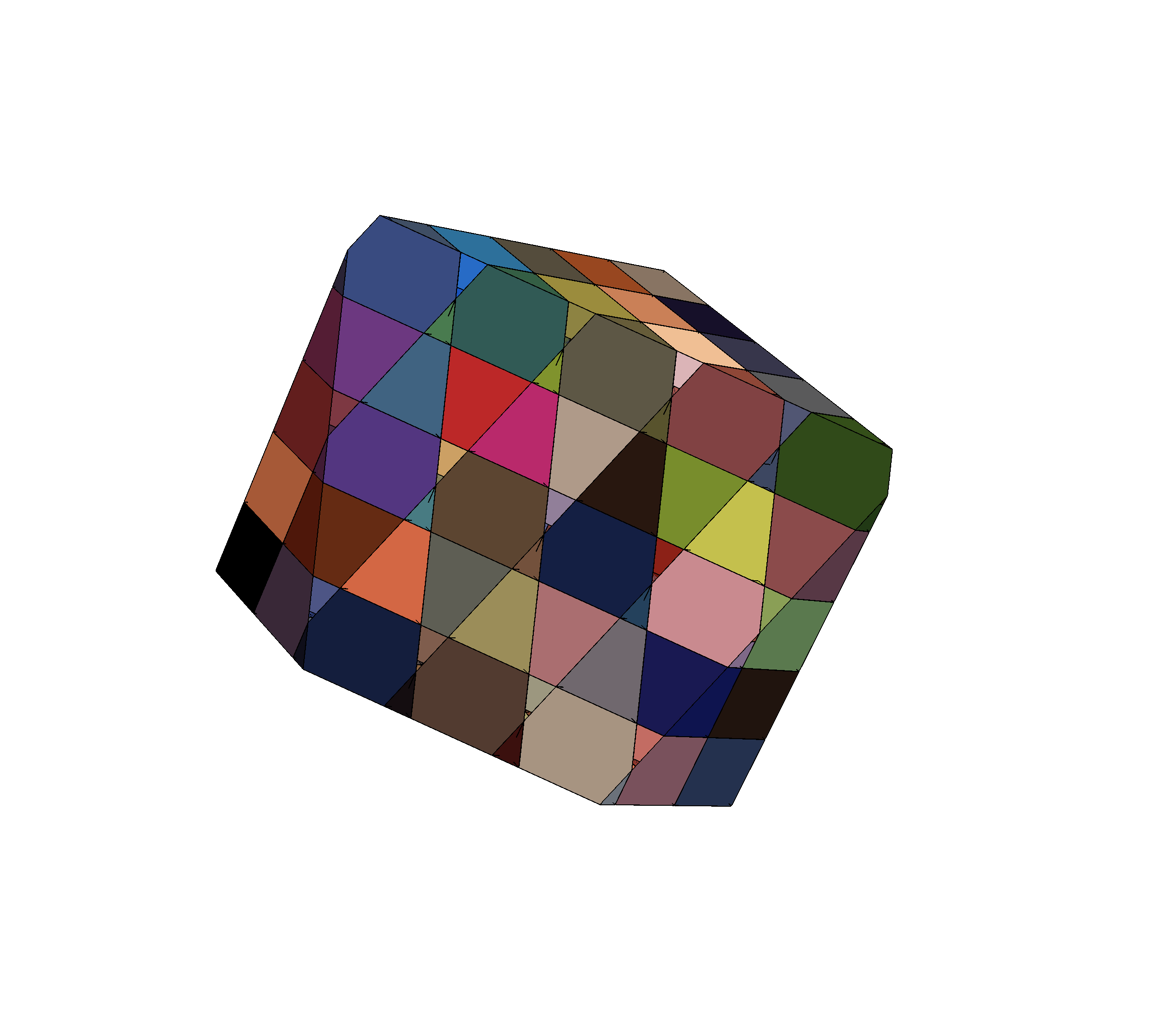
Each color is a basin
Imagine cubic basins in a regular grid
Slicing the energy landscape
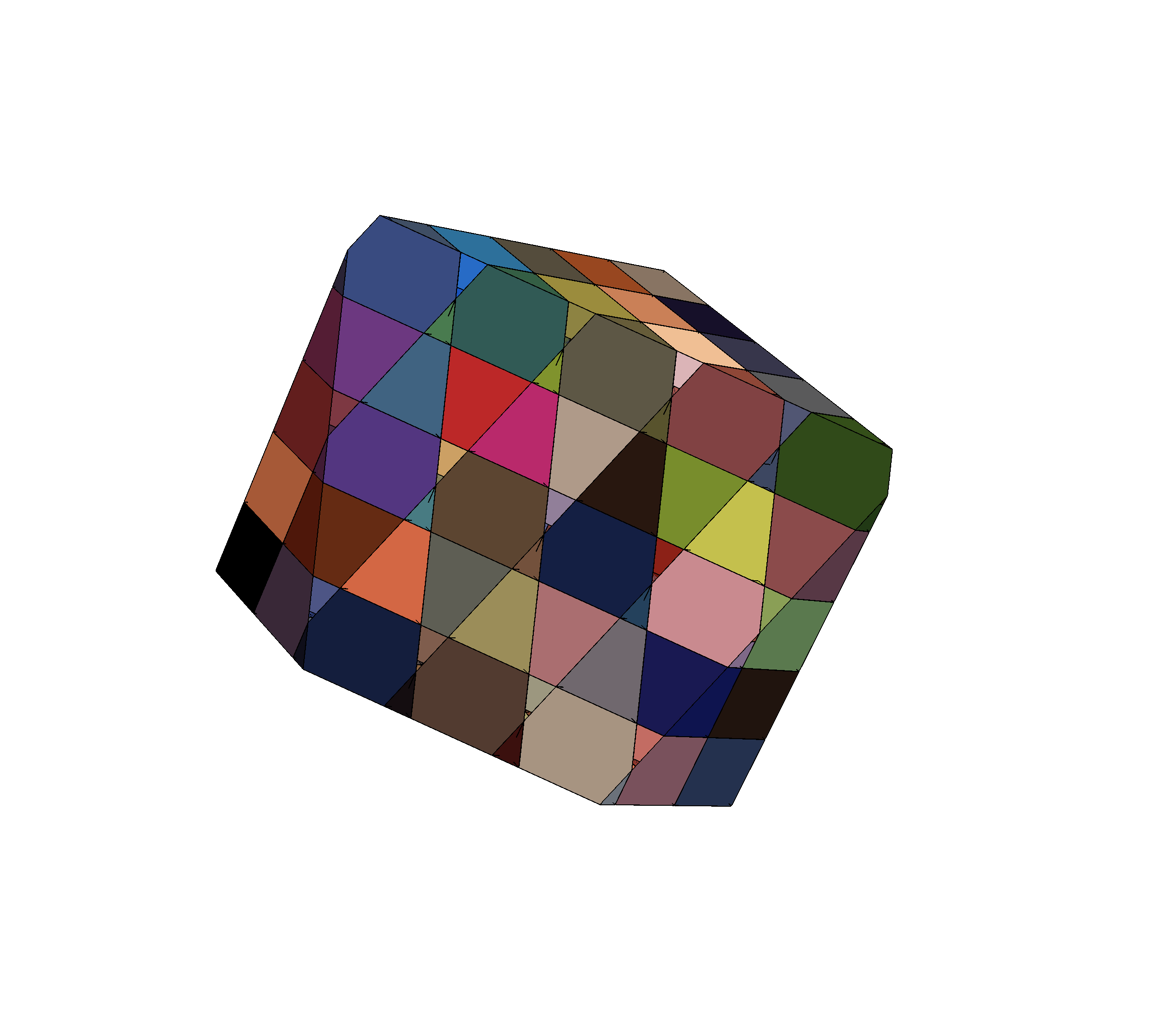
Each color is a basin
Imagine cubic basins in a regular grid
Wales, David. Energy landscapes: Applications to clusters, biomolecules and glasses. Cambridge University Press, 2003.
Basin identification in \(d_l = 3\)
Optimizers give nearly accurate basins in low dimensions !!
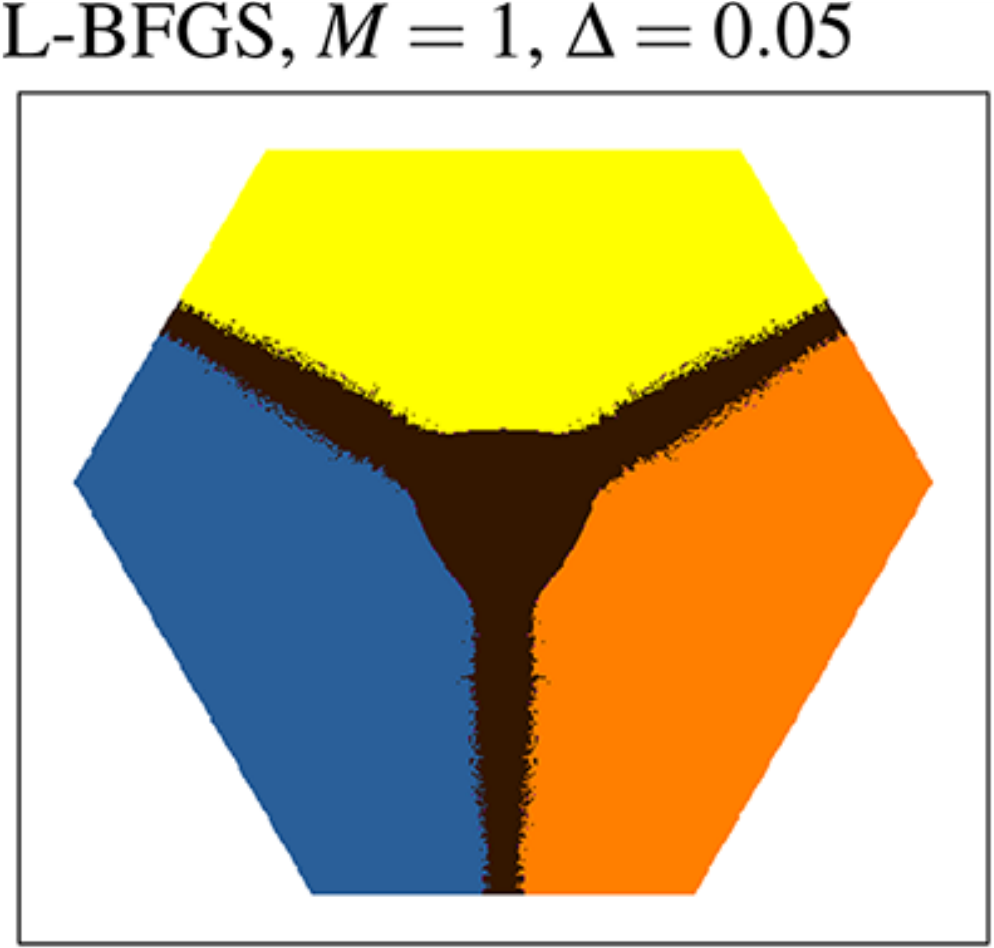
LBFGS
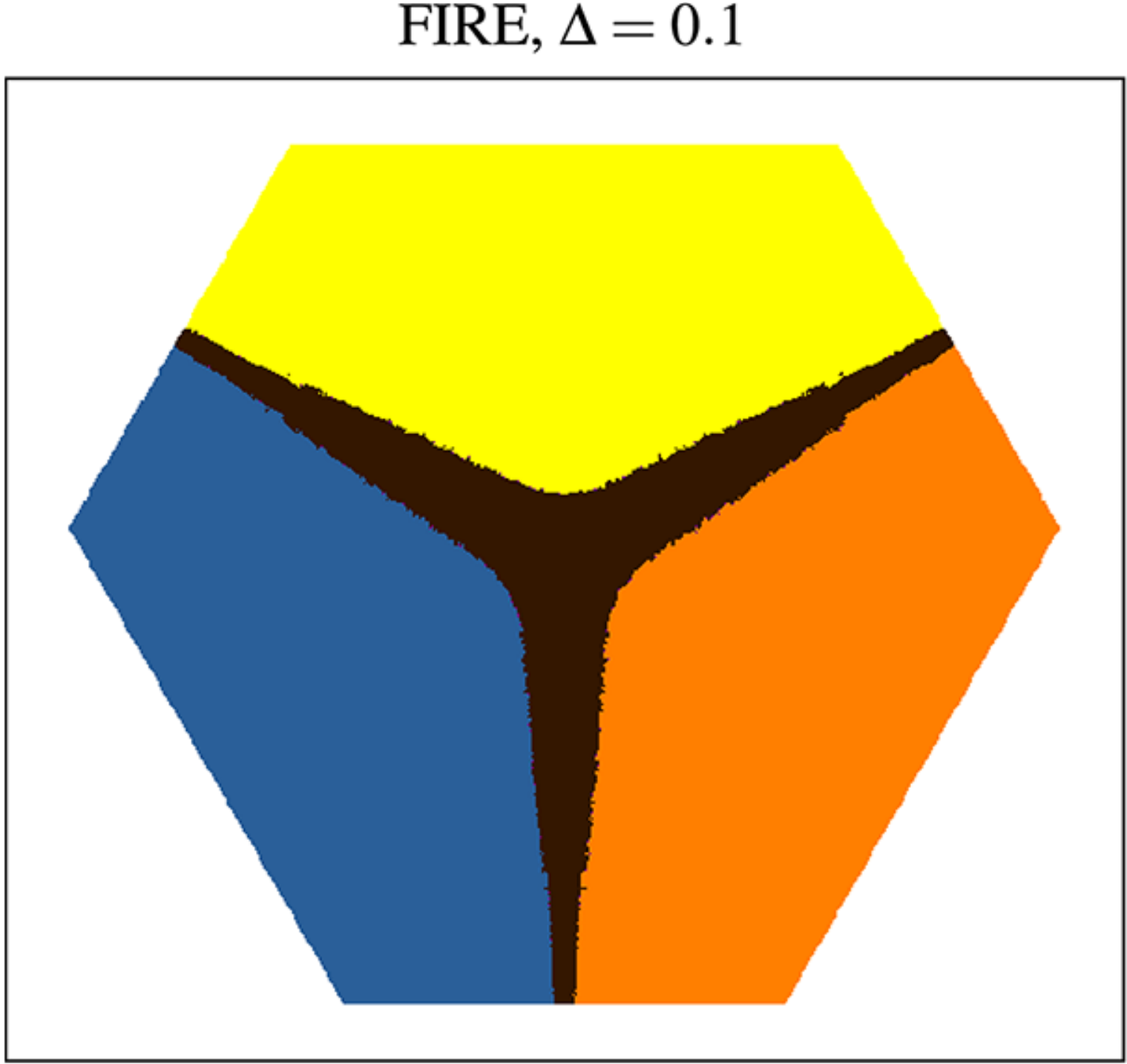
FIRE
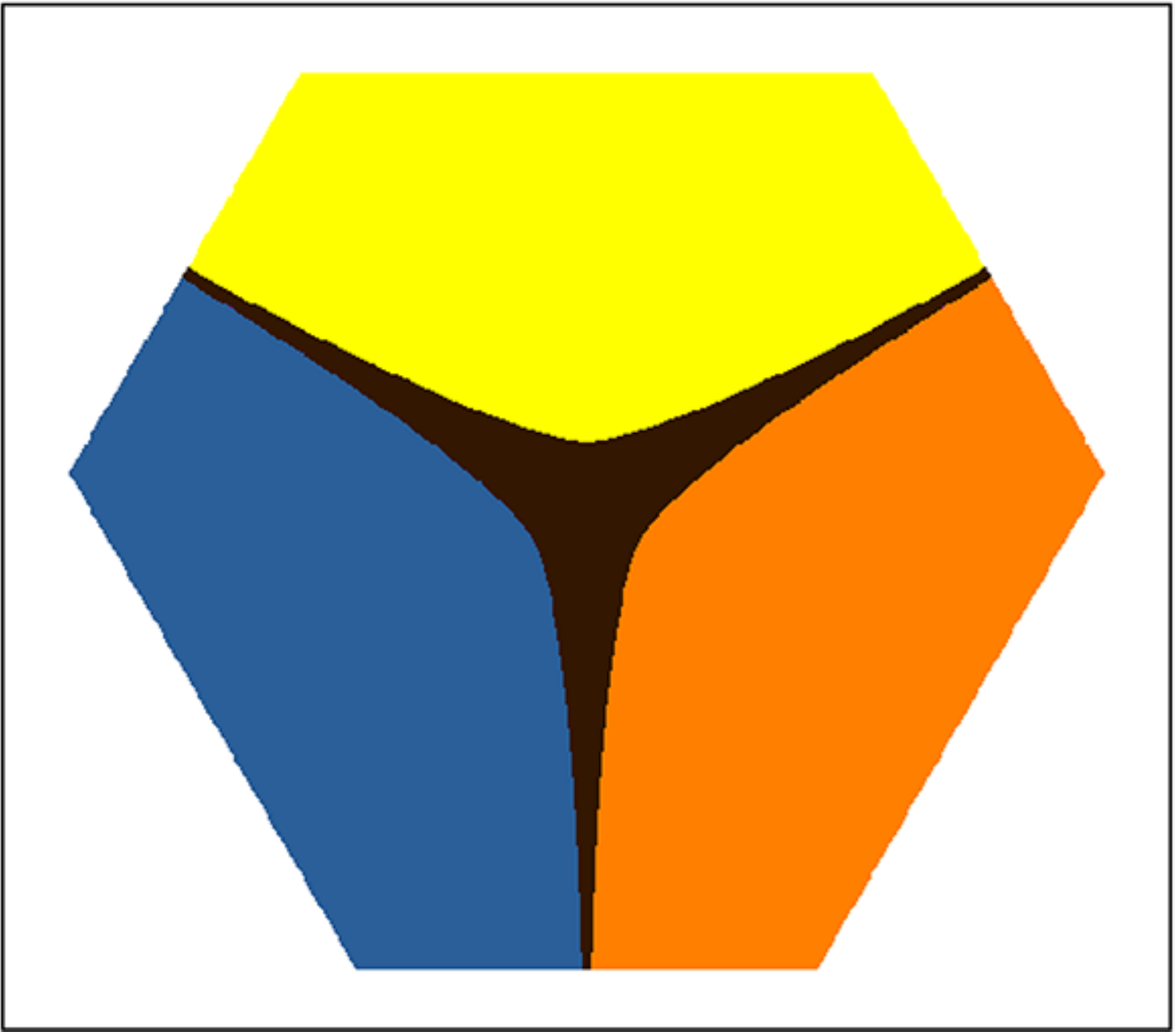
Steepest Descent
16 particle basin slice with FIRE
16 particle basin slice with FIRE
\(d_l \sim 30\)
\(d_l \sim 30\)
ODE Solver Comparison (1024 particles)
Rackauckas, Christopher, et, al., Journal of open research software 5.1 (2017).
Local error
Time (s)

CVODE (Best)
QNDF
Adaptive Implicit Runge Kutta
Adaptive Implicit Euler
Better!
ODE Solver Comparison (1024 particles)
Rackauckas, Christopher, et, al., Journal of open research software 5.1 (2017).
Local error
Time (s)

CVODE (Best)
QNDF
Adaptive Implicit Runge Kutta
Adaptive Implicit Euler
\(\times 10^3\)
16 particle basin slice with CVODE
16 particle basin slice with CVODE
\(d_l \sim 30\)
\(d_l \sim 30\)
Accuracy
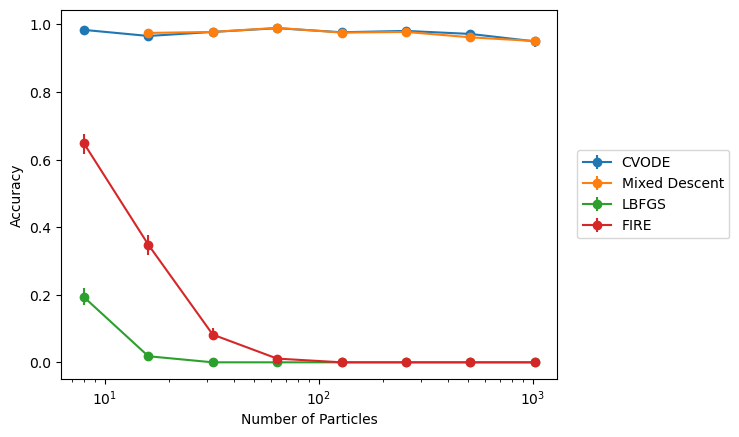
FIRE
LBFGS


FIRE
CVODE
cut around the global minimum: LJ13

\( 8 \times \)equilibrum pairwise distance

Global minimum
\(d_l = 33\)
cut around the global minimum: LJ13

\( 8 \times \)equilibrum pairwise distance

Global minimum
\(d_l = 33\)
Can we do better?: Mixed Descent
$$ V(x) \approx x^T H x $$
Can we do better?: Mixed Descent
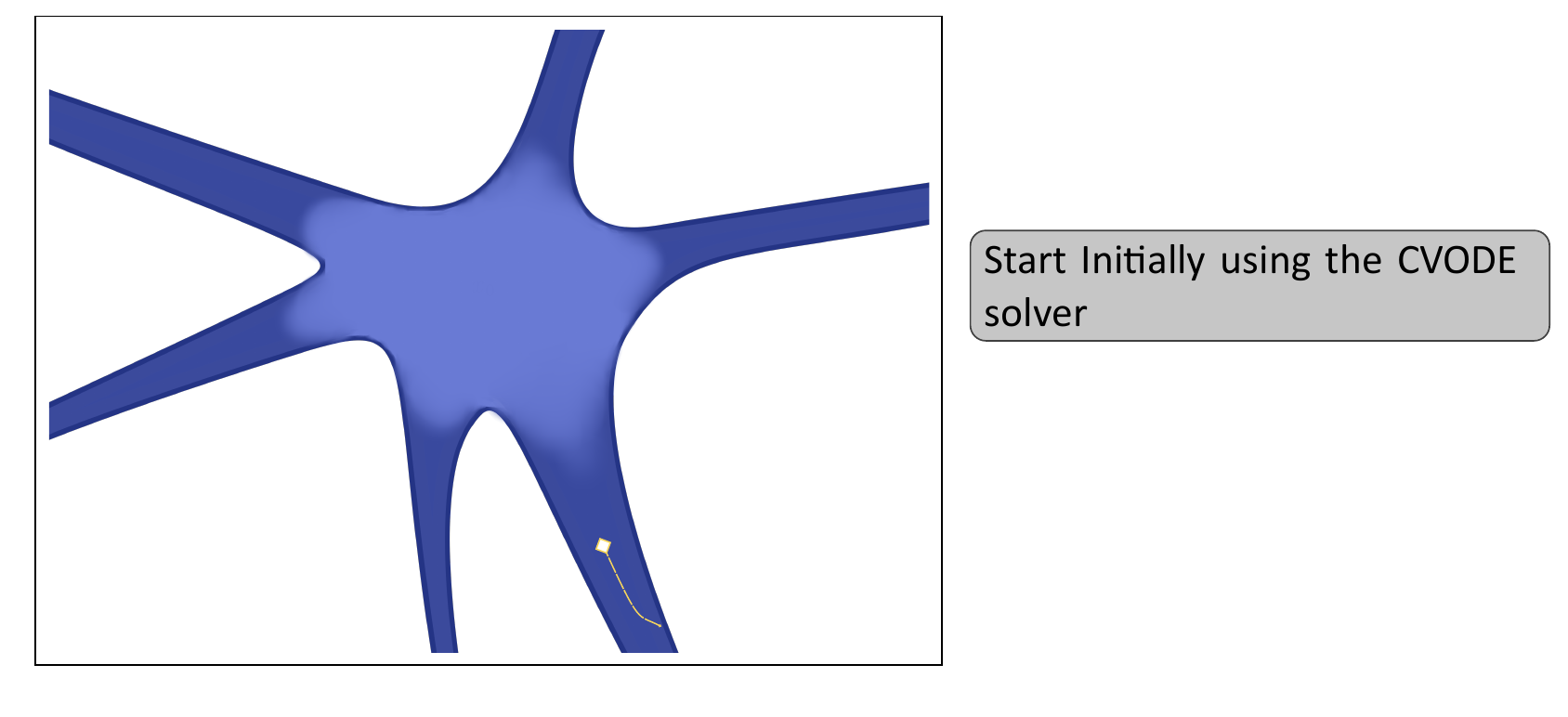
- Start with the CVODE solver
Can we do better?: Mixed Descent
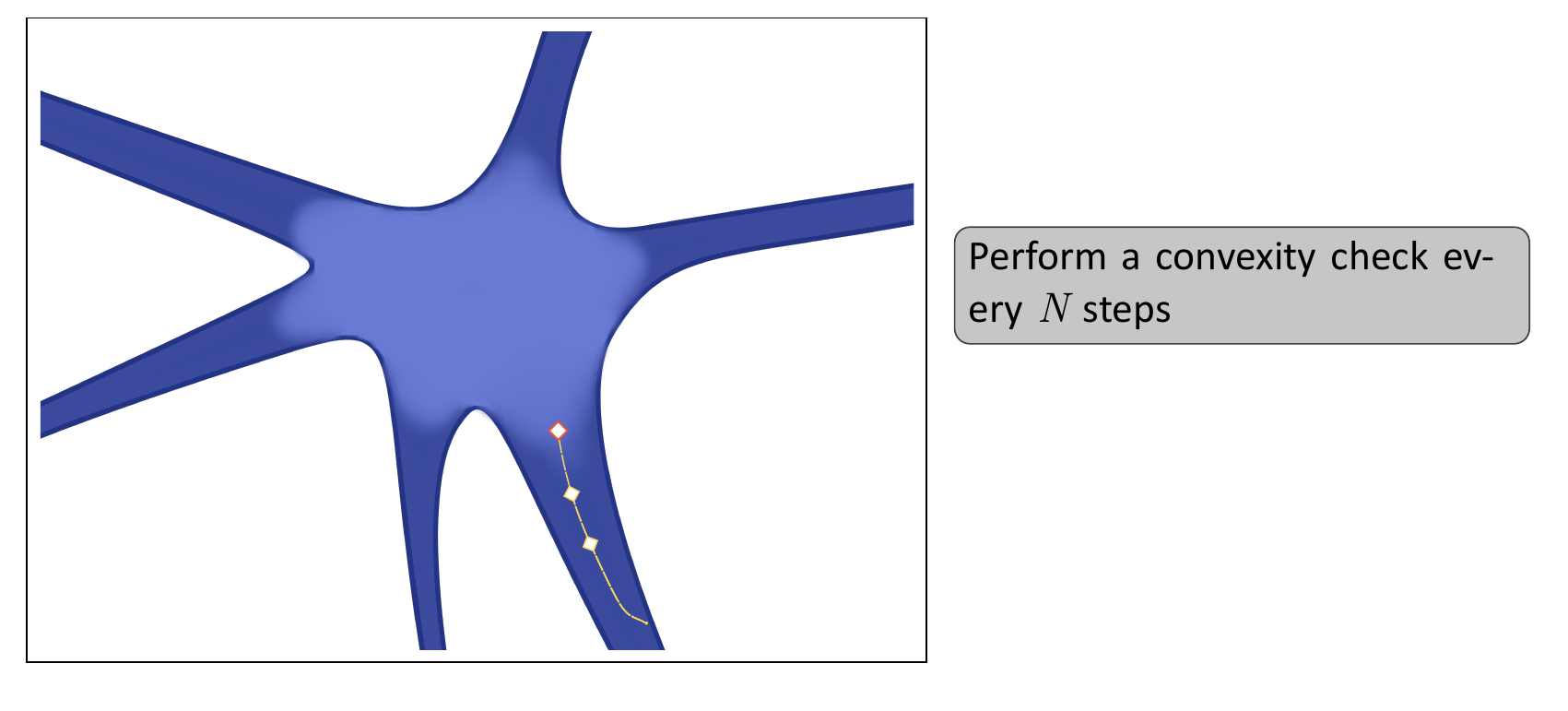
- Start with the CVODE solver
- Perform a convexity check every N iterations
Can we do better?: Mixed Descent
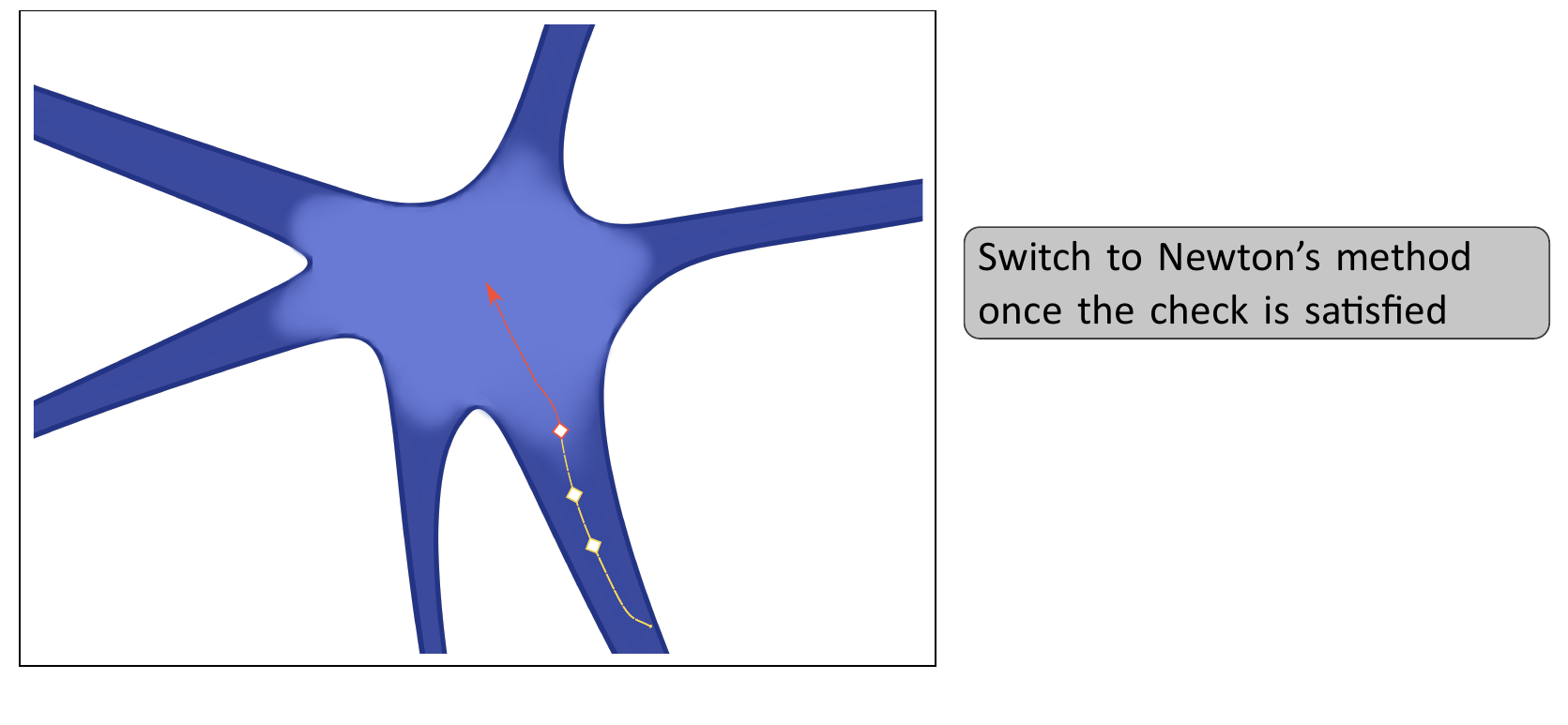
- Start with the CVODE solver
- Perform a convexity check every N iterations
- If convexity check passes, switch to using Newton's method
Can we do better?: Mixed Descent
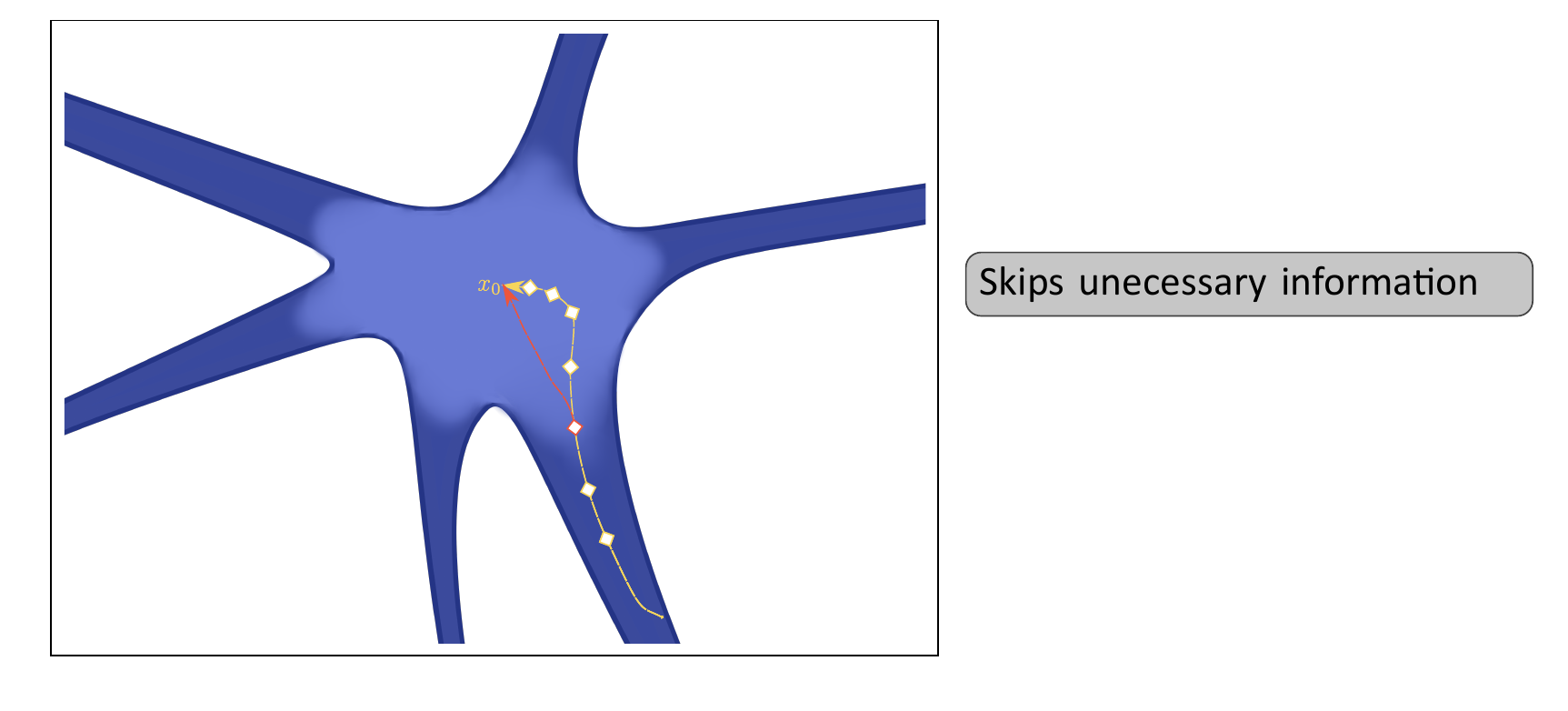
- Start with the CVODE solver
- Perform a convexity check every N iterations
- If convexity check passes, switch to using Newton's method
Skips unnecessary trajectory information!
A fast and accurate algorithm
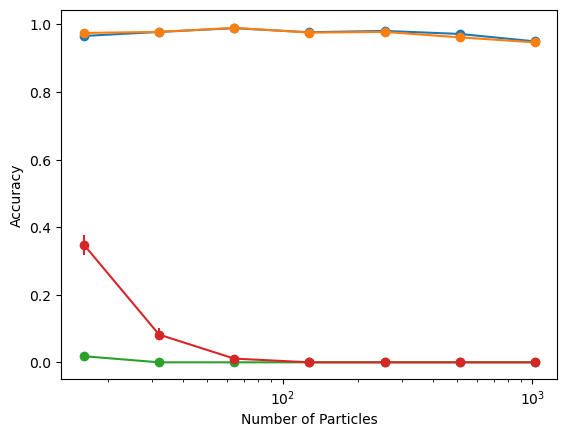
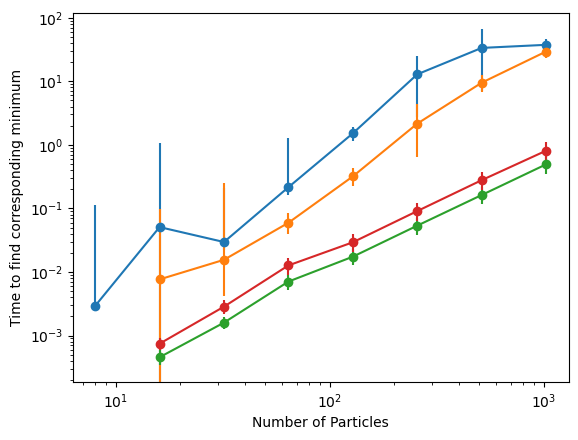
CVODE
Mixed Descent
FIRE
LBFGS
LBFGS
Mixed Descent
CVODE
FIRE
Acknowledgments
Martiniani Lab

Stefano Martiniani

Mathias Casiulis



Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
basin 2
Basin Tiling (What we're interested in)
basin 1
basin 3
Basin identification
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
- Solving steepest descent in \(nD\) for interacting potentials is hard.
- a large volume of previous work mostly relies on optimization algorithms as proxies for finding basins
Method
- Use CVODE to solve the steepest descent equations
- CVODE is much faster than Gradient descent
- CVODE is much faster than scipy implemented stiff ODE methods
- Identify minima/optimize with pele (https://github.com/martiniani-lab/pele). Hard fork of Wales group code with additional functionality implemented
- Code implemented in basinerror (https://github.com/martiniani-lab/basinerror)
Goals for the talk
- I want to show you how to get basins of attraction in high dimensions accurately
- I want to show you how you can get them fast
Accuracy curves: Harmonic potential (2d)

CVODE: Results
How to get Global Accuracy
- Generate \(N\) steepest descent trajectories to the minima at very low \(rtol\) from random initial conditions
- verify that the minima don't change when you increase \(rtol\) $$\frac{N_\text{incorrect}}{N} < 0.01 $$

\(N\)
\(rtol\)
95 percent accuracy
Accuracy curves: Harmonic potential (2d)

Random cut around the "global maximum"
\( 8 \times \)equilibrum pairwise distance

Energy Landscapes
Glasses
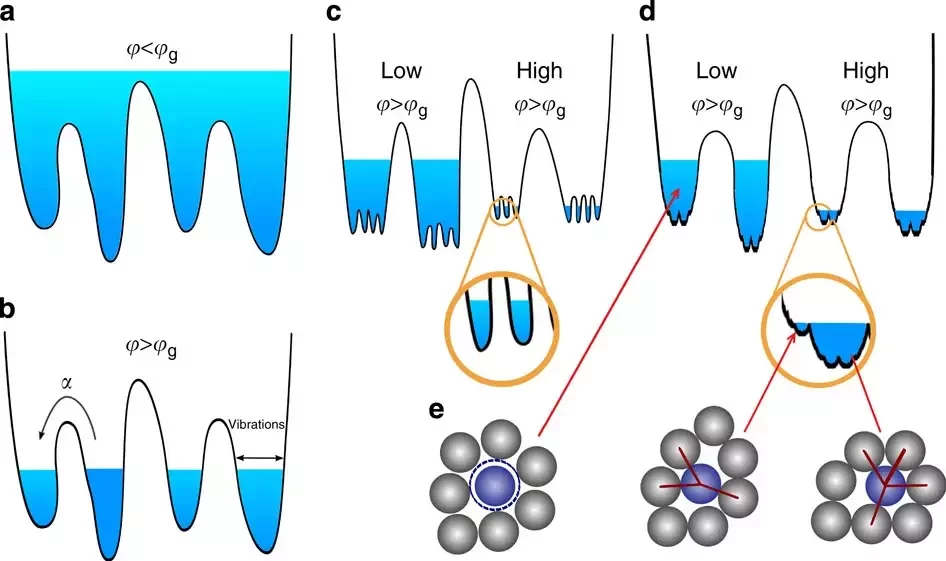
Hierarchical Landscape
Charbonneau, Patrick, et al , Nat Commun 5, 3725 (2014)
Random cut around a local minimum
Random cut around a local minimum LJ 13
\( 8 \times \)equilibrum pairwise distance

\( 8 \times \)equilibrum pairwise distance

Colors not matched!!
Counting by sampling
\(d\)
$$ N_{buildings} = \frac{D}{\langle\mathcal{d}\rangle} $$