Structure of basins of attraction of soft sphere packings
Praharsh Suryadevara
Thesis Defense
NYU
Energy Landscapes

High-dimensional energy landscapes with multiple minima arise across many fields
Glasses
Stillinger, Frank H. Energy landscapes, inherent structures, and condensed-matter phenomena. Princeton University Press, 2015.
Proteins
Onuchic, José Nelson, and Peter G. Wolynes. "Theory of protein folding." Current opinion in structural biology 14.1 (2004): 70-75
Deep Learning
Bengio, Yoshua, Ian Goodfellow, and Aaron Courville. Deep learning. Vol. 1. Cambridge, MA, USA: MIT press, 2017.
and many more....
Energy Landscapes



Energy Landscapes in one dimension

\(V(x)\)
\(x\)
\(x_0\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
\(x_0\)
$$ \frac{d\mathbf{X}}{dt} = -\nabla E(\mathbf{X})$$
Steepest Descent ODE
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
\(x_0\)
$$ \frac{d\mathbf{X}}{dt} = -\nabla E(\mathbf{X})$$
Steepest Descent ODE
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
\(x_0\)
$$ \frac{d\mathbf{X}}{dt} = -\nabla E(\mathbf{X})$$
Steepest Descent ODE
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
$$ \frac{d\mathbf{X}}{dt} = -\nabla E(\mathbf{X})$$
Steepest Descent ODE
\(\mathbf{X}_0\)
\(\mathbf{X}_{min}\)
Energy Landscapes in one dimension

\(V(x)\)
\(x\)
basin 2
Basin tiling (what we're interested in)
basin 1
basin 3
$$ \frac{d\mathbf{X}}{dt} = -\nabla E(\mathbf{X})$$
Steepest Descent ODE
Local Stability

\(V(x)\)
\(x\)
\(\epsilon\)
\(\lambda_i\) are eigenvalues of the Hessian
\(\mathbf{X}_{min}\) is locally stable.
Basins are nonlocal so we can use them to characterize global stability
Krakovská, H., Kuehn, C., & Longo, I. P. (2024). Resilience of dynamical systems. European Journal of Applied Mathematics, 35(1), 155-200.
\[\mathbf{X}'=\mathbf{X}+\mathbf{\epsilon}\]
\[ \frac{d\epsilon}{dt} = -H(\mathbf{X}_{min})\epsilon \]
Linear Stability Analysis
\[\epsilon'_i(t) = \epsilon'_i(0) e^{-\lambda_i t}\]
Global Stability
Initial state sensitivity
Basin Volumes

McDonald, S. W., Grebogi, C., Ott, E., & Yorke, J. A. (1985). Fractal basin boundaries. Physica D: Nonlinear Phenomena, 17(2), 125-153.
Wiley, D. A., Strogatz, S. H., & Girvan, M. (2006). The size of the sync basin. Chaos: An Interdisciplinary Journal of Nonlinear Science, 16(1).
Menck, P. J., Heitzig, J., Marwan, N., & Kurths, J. (2013). How basin stability complements the linear-stability paradigm. Nature physics, 9(2), 89-92.
Bidisperse Hertzian soft spheres
\(\phi=0.845\)
$$ V_{ij}(r) =\begin{cases} \frac{\epsilon}{p} \left( 1 - \frac{r}{r_{i} + r_{j}} \right) ^{p} & r < r_{i} + r_{j} \\ 0 & r > r_{i} + r_{j}\end{cases}$$ with \(p\) = 2.5 and packing fraction \(\phi> \phi_j\)
\(d_l \sim (N-1)\times d\)
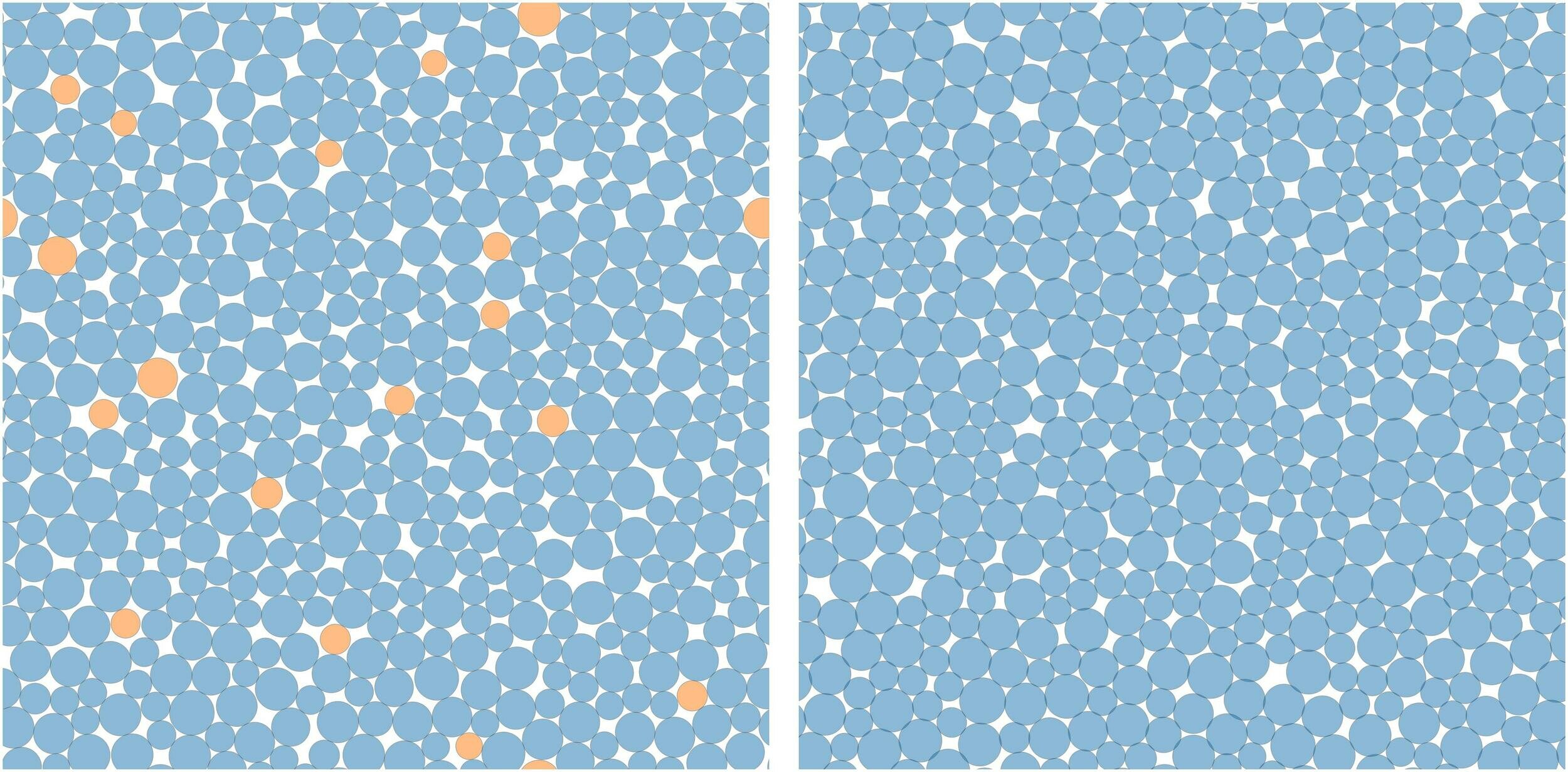
\(\phi=0.9\)
Roadmap
How do you identify a basin
Fractality/initial state sensitivity
Basin Volumes
Basin identification in \((N-1)\times d\) dimensions
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
Newton/Quasi-Newton methods (e.g. LBFGS)
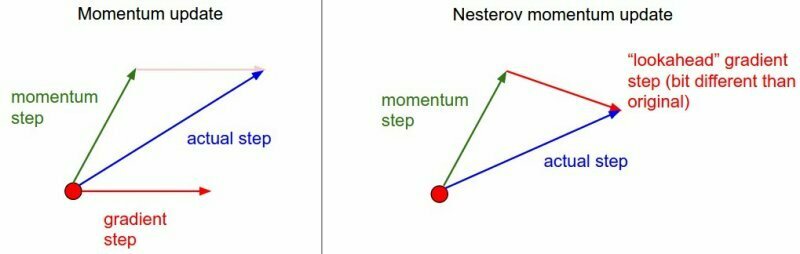
Momentum-based optimizers (e.g. FIRE)
Time
$$ x_{t+\Delta t} = x_t + \Delta t \nabla V(x_t)$$
Gradient Descent/Forward Euler infinitesimal stepsizes
Error
Optimizers accurate for small systems but not benchmarked moderate/large systems
??
Basin identification in \((N-1)\times d\) dimensions
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
Optimizers
Forward Euler/Gradient descent
ODE Solvers
Expensive/Infeasible in high dimensions
Faster but accurate Methods?

Newton/Quasi-Newton methods (e.g. LBFGS)

Momentum-based optimizers (e.g. FIRE)
Basin identification in \((N-1)\times d\) dimensions
$$ \frac{\text{d} x}{\text{d} t} = - \nabla V(x)$$
steepest descent
- Solving steepest descent in \((N-1) \times D\) for interacting potentials is expensive
- Previous work mostly relies on optimization algorithms as proxies for finding basins

Momentum-based optimizers (e.g. FIRE)

Newton/Quasi-Newton methods (e.g. LBFGS)
https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
Goal of this Talk
I want to show you, with new physics along the way, how to get features of the energy landscape accurately
Basin identification in \((N-1)\times d\) dimensions
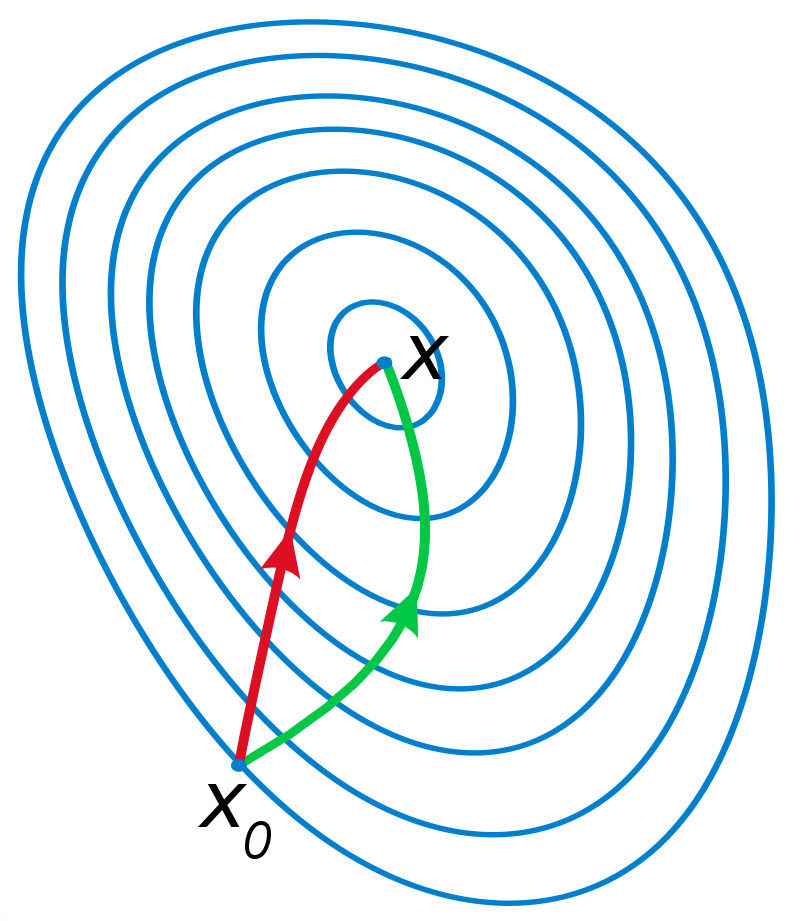
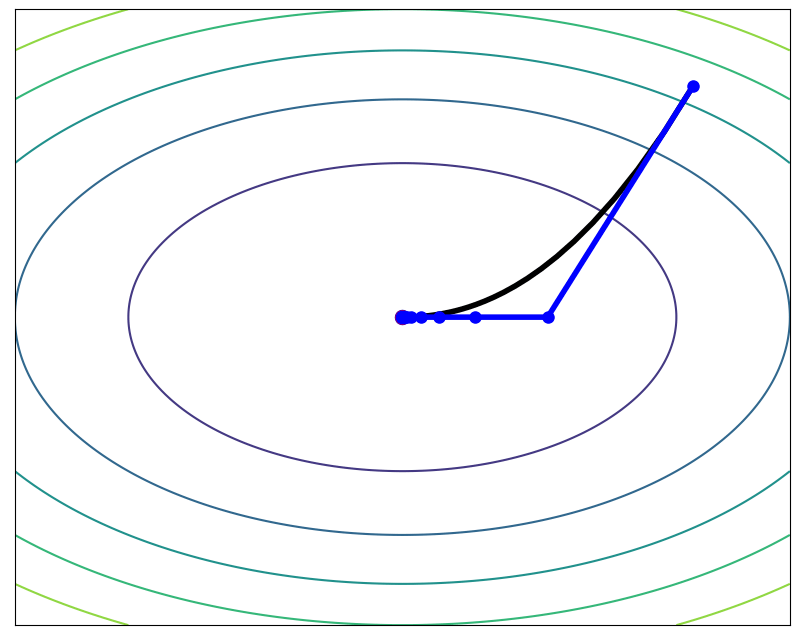
If your basin is a bowl it does not matter what path you take

L-BFGS
Forward Euler (Gradient Descent)
FIRE (Modified)
Basin identification in \((N-1)\times d\) dimensions
1985: First mentioned use of only an optimizer
Stillinger, F. H., & Weber, T. A. (1985). Computer simulation of local order in condensed phases of silicon. Physical review B, 31(8), 5262-5271.
1982: Inherent structure formalism
Stillinger, F. H., & Weber, T. A. (1982). Hidden structure in liquids. Physical Review A, 25(2), 978.
Treatment as an optimization problem started ~40 years ago
Chakravarty, C., Debenedetti, P. G., & Stillinger, F. H. (2005). Generating inherent structures of liquids: Comparison of local minimization algorithms. The Journal of chemical physics, 123(20).
2005/2013: Comparison between different optimizers without ground truth/for small systems
Asenjo, D., Stevenson, J. D., Wales, D. J., & Frenkel, D. (2013). Visualizing basins of attraction for different minimization algorithms. The Journal of Physical Chemistry B, 117(42), 12717-12723.
System: Repulsive Soft spheres
Bidisperse Hertzian soft spheres

$$ V_{ij}(r) =\begin{cases} \frac{\epsilon}{p} \left( 1 - \frac{r}{r_{i} + r_{j}} \right) ^{p} & r < r_{i} + r_{j} \\ 0 & r > r_{i} + r_{j}\end{cases}$$ with \(p\) = 2.5 and packing fraction \(\phi> \phi_j\)

landscape dimension \(d_l \sim (N-1)\times d\)
Basin identification in \((N-1)\times d\) dimensions
Conflating finding attractors of the steepest descent ODE with minimization leads to artificial issues
"This shows that mapping an equilibrium liquid state to an inherent structure is a fully dynamical problem, which becomes uniquely defined only after a specific choice for the minimisation algorithm is
made"
Nishikawa, Y., Ozawa, M., Ikeda, A., Chaudhuri, P., & Berthier, L. (2022). Relaxation dynamics in the energy landscape of glass-forming liquids. Physical Review X, 12(2), 021001.
"Because the process [integration] is
chaotic, changing [algorithm parameters] changes an individual IS
determination"
Charbonneau, P., & Morse, P. K. (2023). Jamming, relaxation, and memory in a minimally structured glass former. Physical Review E, 108(5), 054102.
Bautista, E., & Corwin, E. I. (2025). Numerically Discovered Inherent States are Always Protocol Dependent in Jammed Packings. arXiv preprint arXiv:2508.09284.
"As a result,
it is practically impossible to reliably find inherent states
for systems of more than about 64 particles."
Basin identification in \((N-1)\times d\) dimensions
I will show you how to identify basins accurately upto $$N=1024$$
Stiffness: Explicit solvers
\[\mathbf{X}'=\mathbf{X}+\mathbf{\epsilon}\]
\[ \frac{d\epsilon}{dt} = -H(\mathbf{X}_{min})\epsilon \]
Linear Stability Analysis
\[\epsilon'_i(t) = \epsilon'_i(0) e^{-\lambda_i t}\]
$$ \Delta t < \frac{2}{|\lambda_{\max}|} $$
$$\mathbf{X}_{k+1} = \mathbf{X}_k (1-\lambda \Delta t )$$
$$\mathbf{X}_{k+n} = \mathbf{X}_k (1-\lambda \Delta t )^n$$
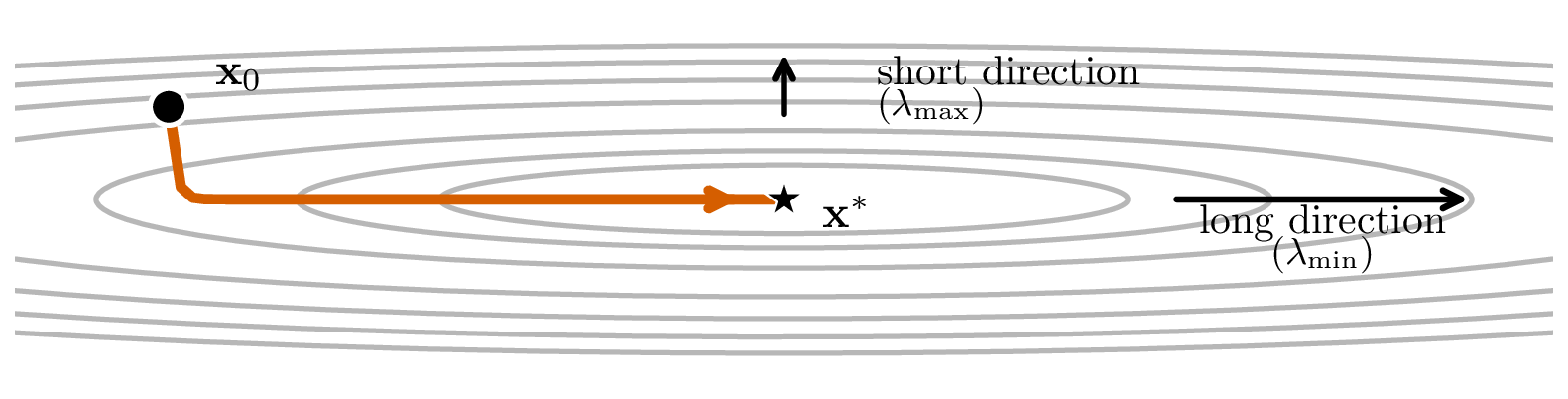
Most effort is in the long direction, but step size is constrained by the shortest direction
Forward Euler Update
Stiffness: Explicit solvers
$$ \Delta t < \frac{2}{|\lambda_{\max}|} $$
$$\mathbf{X}_{k+1} = \mathbf{X}_k (1-\lambda \Delta t )$$
$$\mathbf{X}_{k+n} = \mathbf{X}_k (1-\lambda \Delta t )^n$$
Forward Euler Update
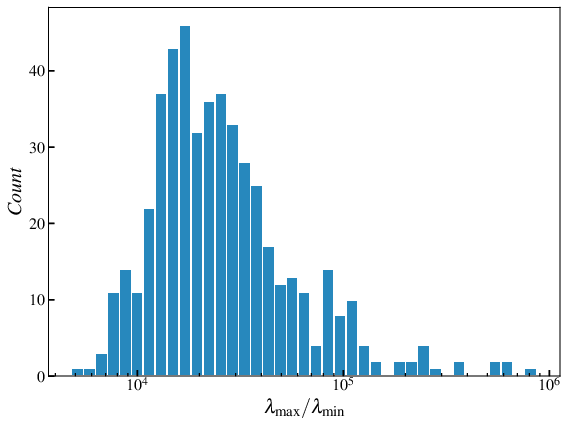
Distribution of \(\lambda_{\max}/\lambda_{\min}\) for \(N=512\) at \(\phi=0.845\)
Stiffness: Implicit solvers
\[\mathbf{X}'=\mathbf{X}+\mathbf{\epsilon}\]
\[ \frac{d\epsilon}{dt} = -H(\mathbf{X}_{min})\epsilon \]
Linear Stability Analysis
\[\epsilon'_i(t) = \epsilon'_i(0) e^{-\lambda_i t}\]
No stability limit on \(\Delta t\)!! Step size is chosen on accuracy alone
$$\mathbf{X}_{k+1} = \mathbf{X}_k-\lambda \Delta t \mathbf{X}_{k+1}$$
$$ \mathbf{X}_{k+1} =\frac{\mathbf{X}_k}{1 + \lambda \, \Delta t}$$
ODE Solver Comparison
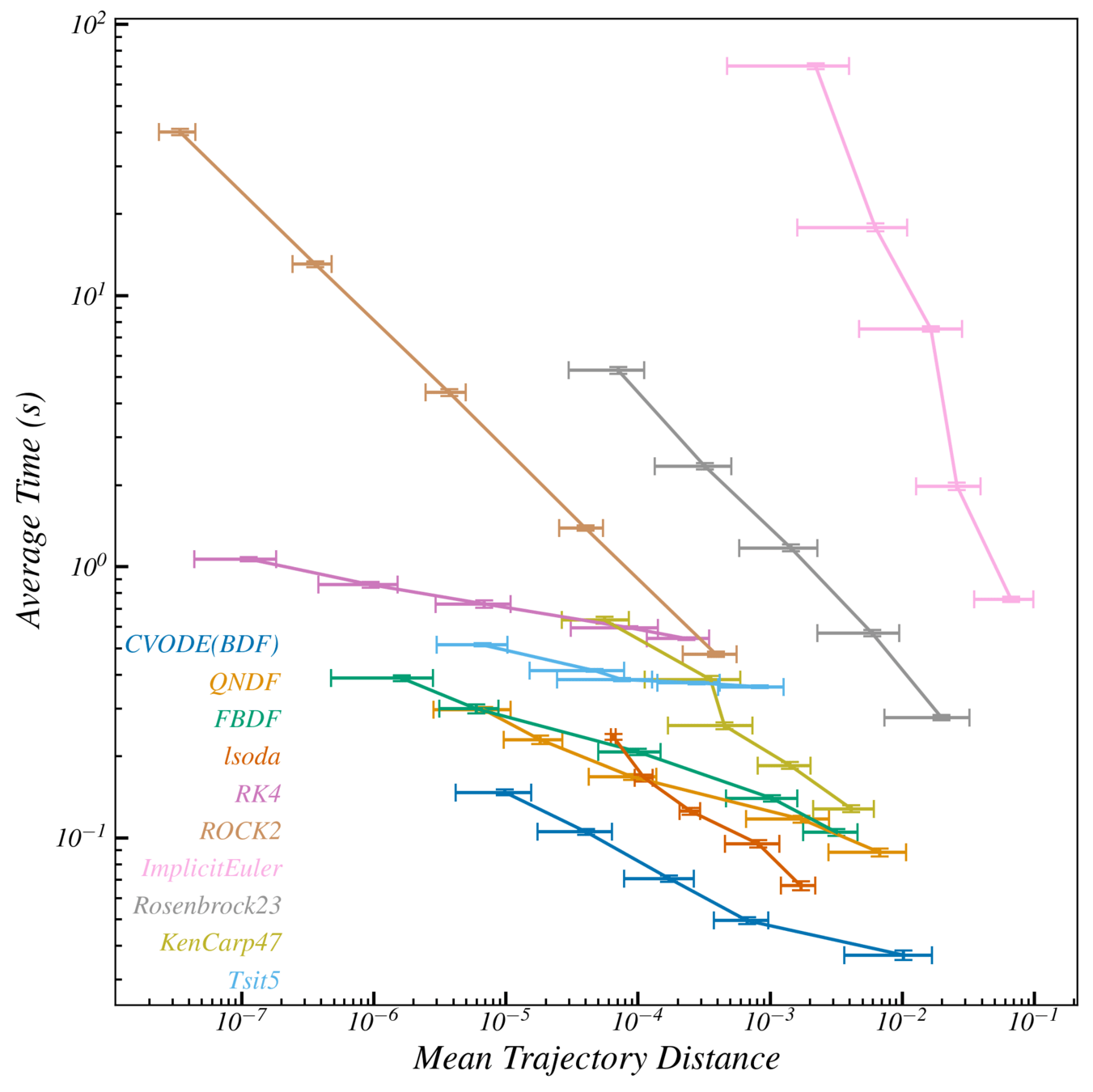
Better
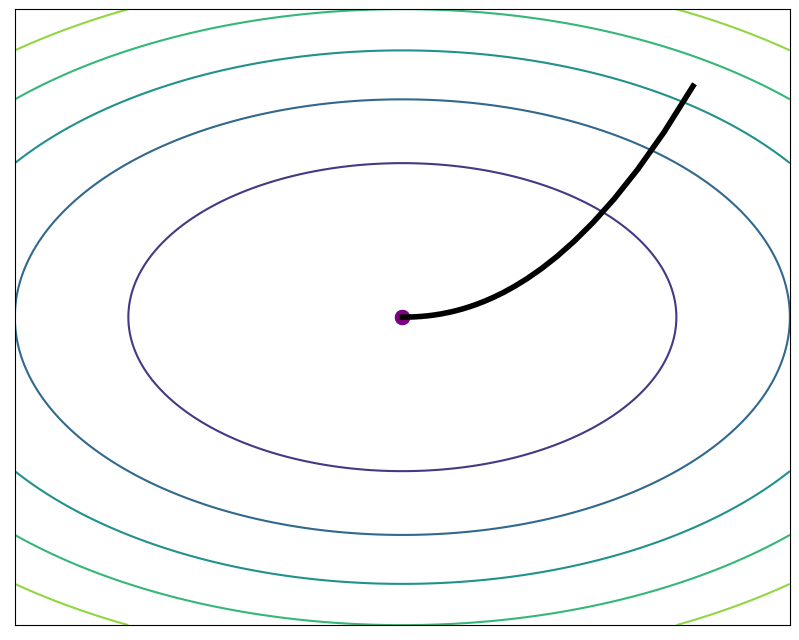
true solution
ODE Solver Comparison

3 orders of magnitude faster than Implicit Euler at same error
Better
ODE solver solution
Max distance
Average over a 100 initial conditions
Stiffness: Working definition


ODE solver solution
Max distance
Average over a 100 initial conditions
Hairer, Ernst, Gerhard Wanner, and Syvert P. Nørsett. Solving ordinary differential equations I: Nonstiff problems. Berlin, Heidelberg: Springer Berlin Heidelberg, 1993.
Stiff equations are equations where certain implicit methods, in particular BDF perform better, usually tremendously better than explicit ones
4x
Slicing the energy landscape

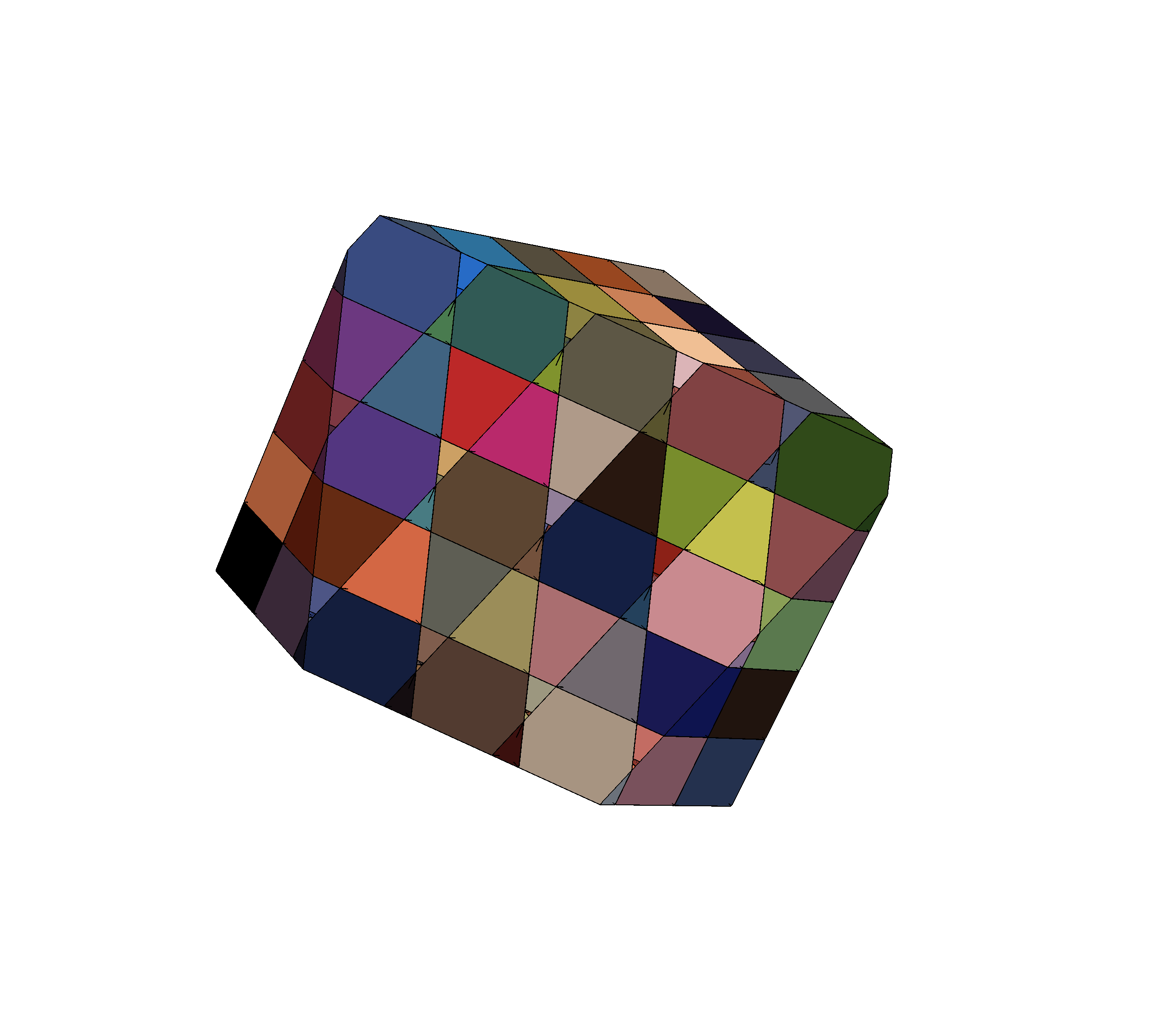
Each color is a basin
Imagine cubic basins in a regular grid
Slicing the energy landscape
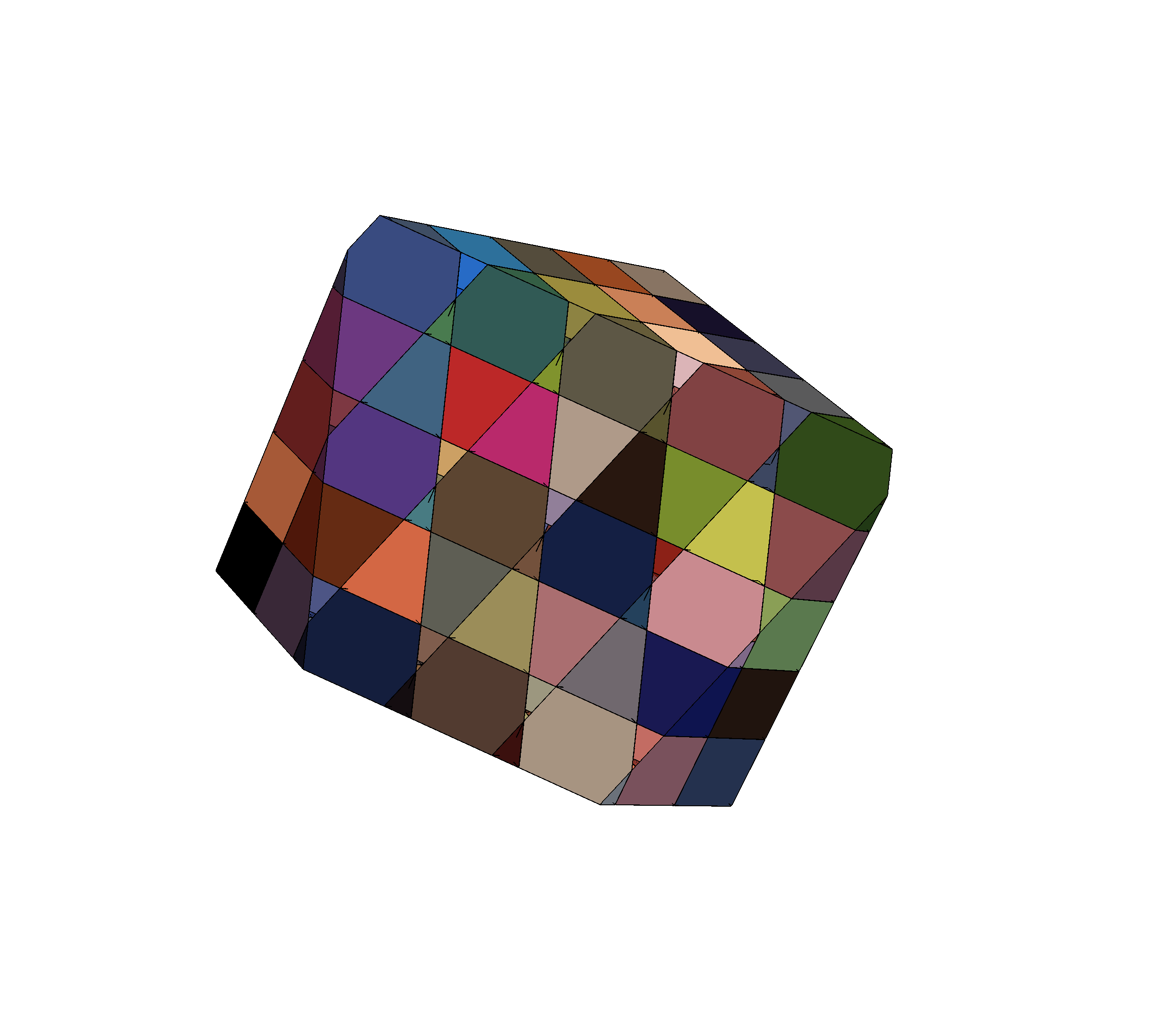
Each color is a basin
Imagine cubic basins in a regular grid
16 particle basin slice with FIRE
16 particle basin slice with FIRE
\(d_l \sim (N-1) d = 30\)
\(d_l \sim (N-1) d = 30\)
16 particle basin slice with FIRE
16 particle basin slice with FIRE
\(d_l \sim (N-1) d = 30\)
\(d_l \sim (N-1) d = 30\)
16 particle basin slice with CVODE
16 particle basin slice with CVODE
\(d_l \sim (N-1) d = 30\)
\(d_l \sim (N-1) d = 30\)
Exact Basins: 8 particles
Accuracy vs System Size
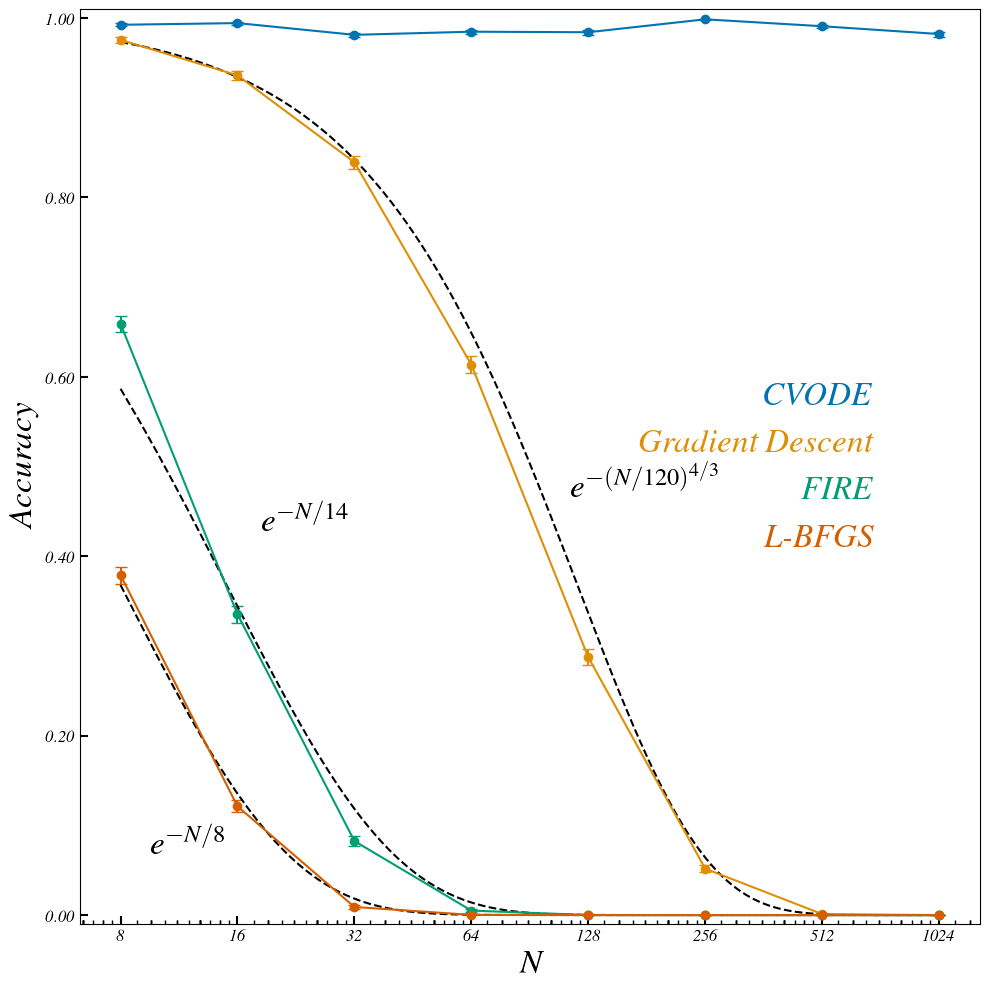
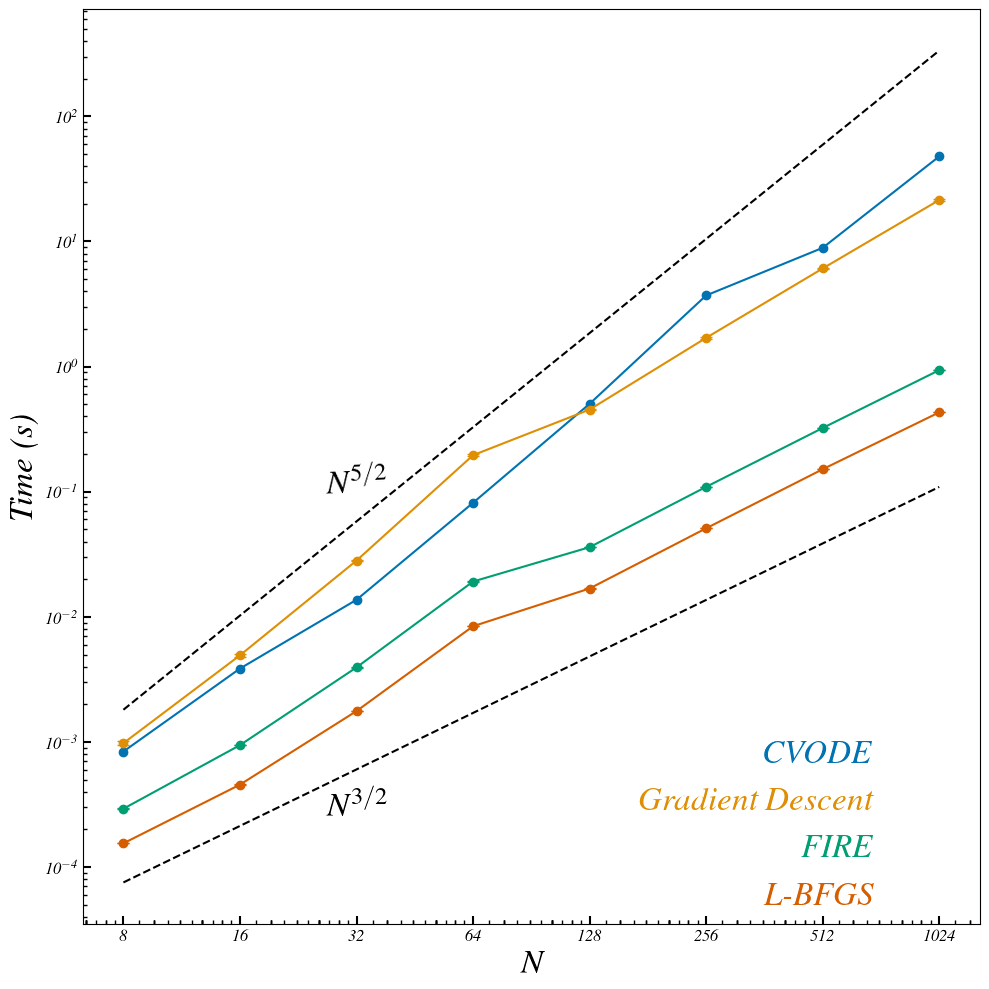
Accuracy



CVODE
FIRE
LBFGS
\(d_l \sim 254\)
\(N \sim 128 \)
Not a single sampled point matches
Areas to Volumes
\(V \sim l^d\)
\(log(V) \sim \log(l_1) + \log(l_2) + ...\)
The limiting distribution of \log(V) should go as Normal, if the mean and variance are well behaved and \(l\) isn't drawn from an already stable distribution
Summary: Accuracy
- The steepest descent ODE for soft sphere packings is stiff
- It is stiff in the linear stability sense, Hessian eigenvalues span many orders of magnitude,
- It is stiff through the working definition; stiff equations are those where implicit methods perform much better than explicit ones
- This allow us to identify correct inherent structures for soft sphere packings at system sizes
- Optimizers give rise to artifacts in basin slices
Roadmap
How do you identify a basin
Fractality/initial state sensitivity
Basin Volumes
Sensitivity
Charbonneau, P., & Morse, P. K. (2023). Jamming, relaxation, and memory in a minimally structured glass former. Physical Review E, 108(5), 054102.
(very non-rigorous) claims of chaoticity from sensitivity
Nishikawa, Y., Ozawa, M., Ikeda, A., Chaudhuri, P., & Berthier, L. (2022). Relaxation dynamics in the energy landscape of glass-forming liquids. Physical Review X, 12(2), 021001.
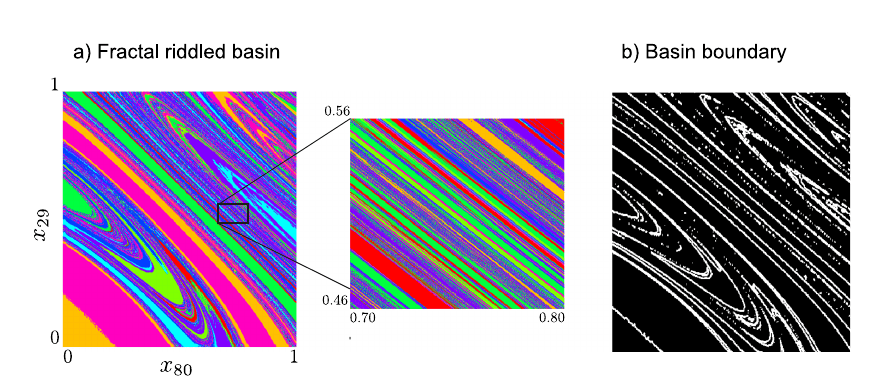
Fractal boundaries
Wales, D. J. (1992). Basins of attraction for stationary points on a potential-energy surface. Journal of the Chemical Society, Faraday Transactions, 88(5), 653-657.
Initial state sensitivity

McDonald, S. W., Grebogi, C., Ott, E., & Yorke, J. A. (1985). Fractal basin boundaries. Physica D: Nonlinear Phenomena, 17(2), 125-153.
Give a fractal dimension for boundaries
Distribution of lengths of basins
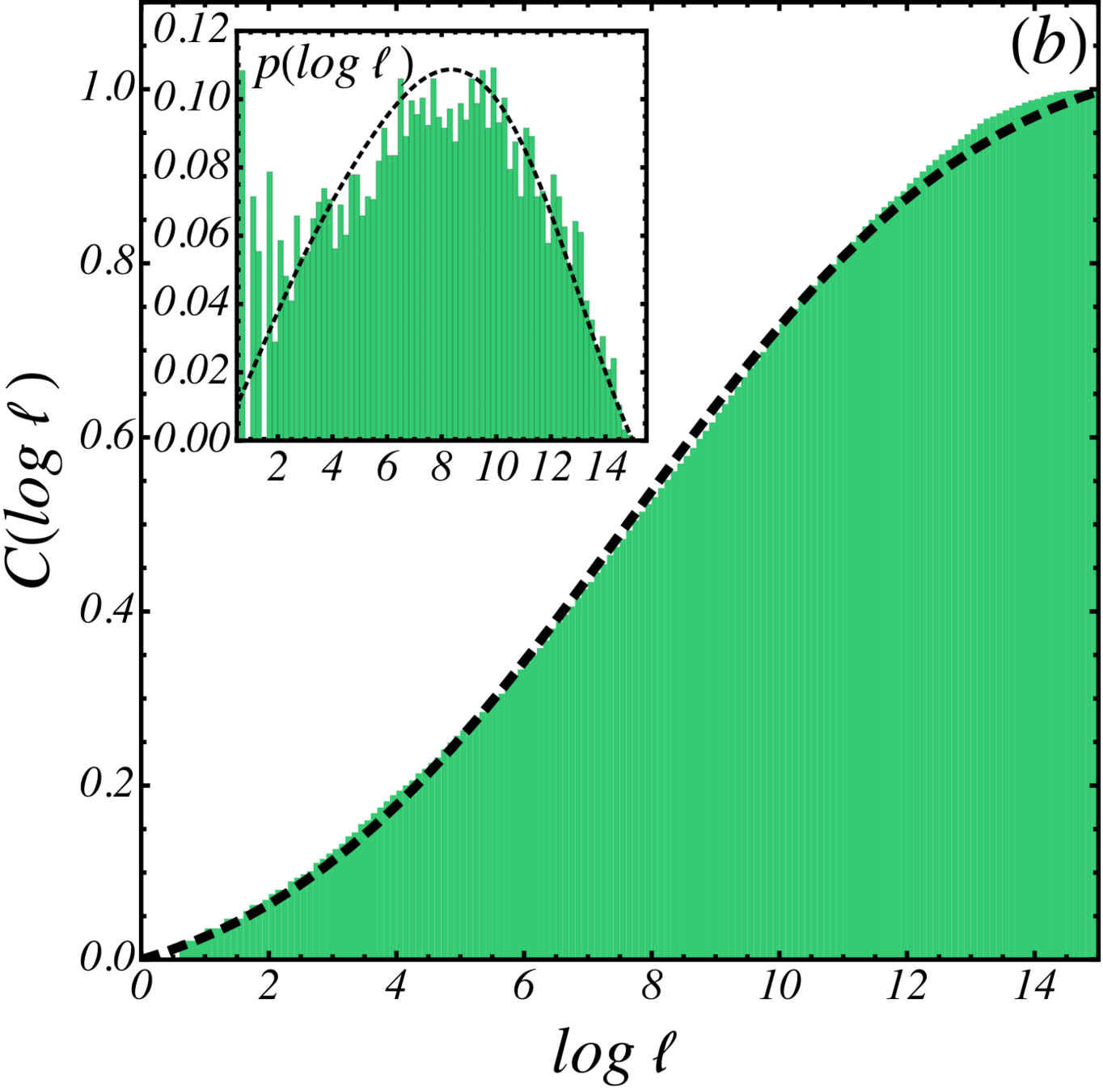
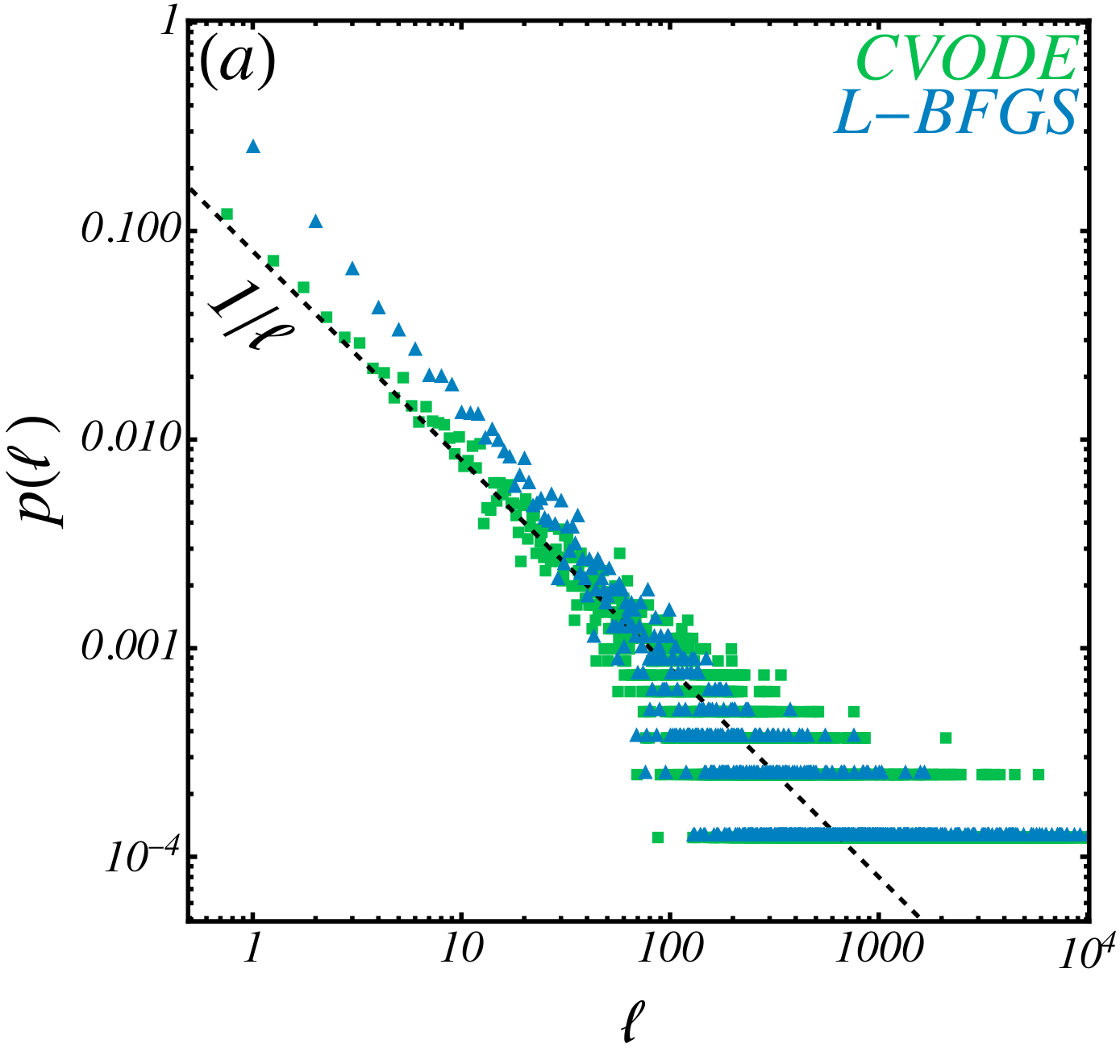
\(N=16\) \(d_l \sim 30\)

Measuring fractal dimension

\(d_B = \lim_{\epsilon\rightarrow 0} \frac{\log N(\epsilon)}{\log(1/\epsilon)}\)
Fractal dimension
\(d_b \sim (1.3, 1.8) \)
Bollt, Erik, et al. "Fractal basins as a mechanism for the nimble brain." Scientific Reports 13.1 (2023): 20860.
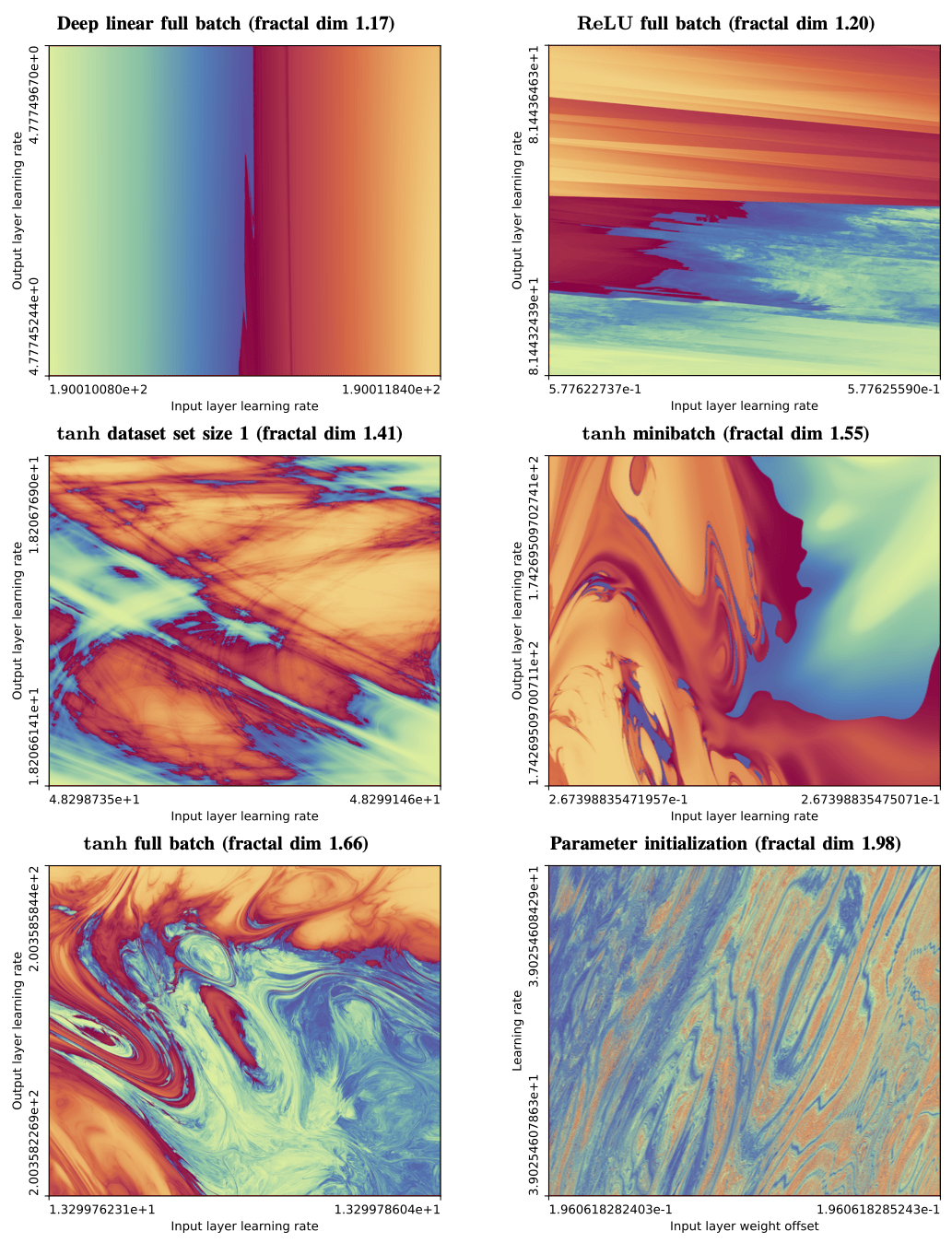
\(d_B\sim1.98\)
https://sohl-dickstein.github.io/2024/02/12/fractal.html
Ly, Andrew, and Pulin Gong. "Optimization on multifractal loss landscapes explains a diverse range of geometrical and dynamical properties of deep learning." Nature Communications 16.1 (2025): 3252.
\( \frac{d\bm{x_{i}}}{dt} = f(\bm{x_{i}}) + \sigma \sum_{j=1}^{N} \left[ A \right]_{ij} h(\bm{x}_{i}, \bm{x}_j)\)
Fractal dimension
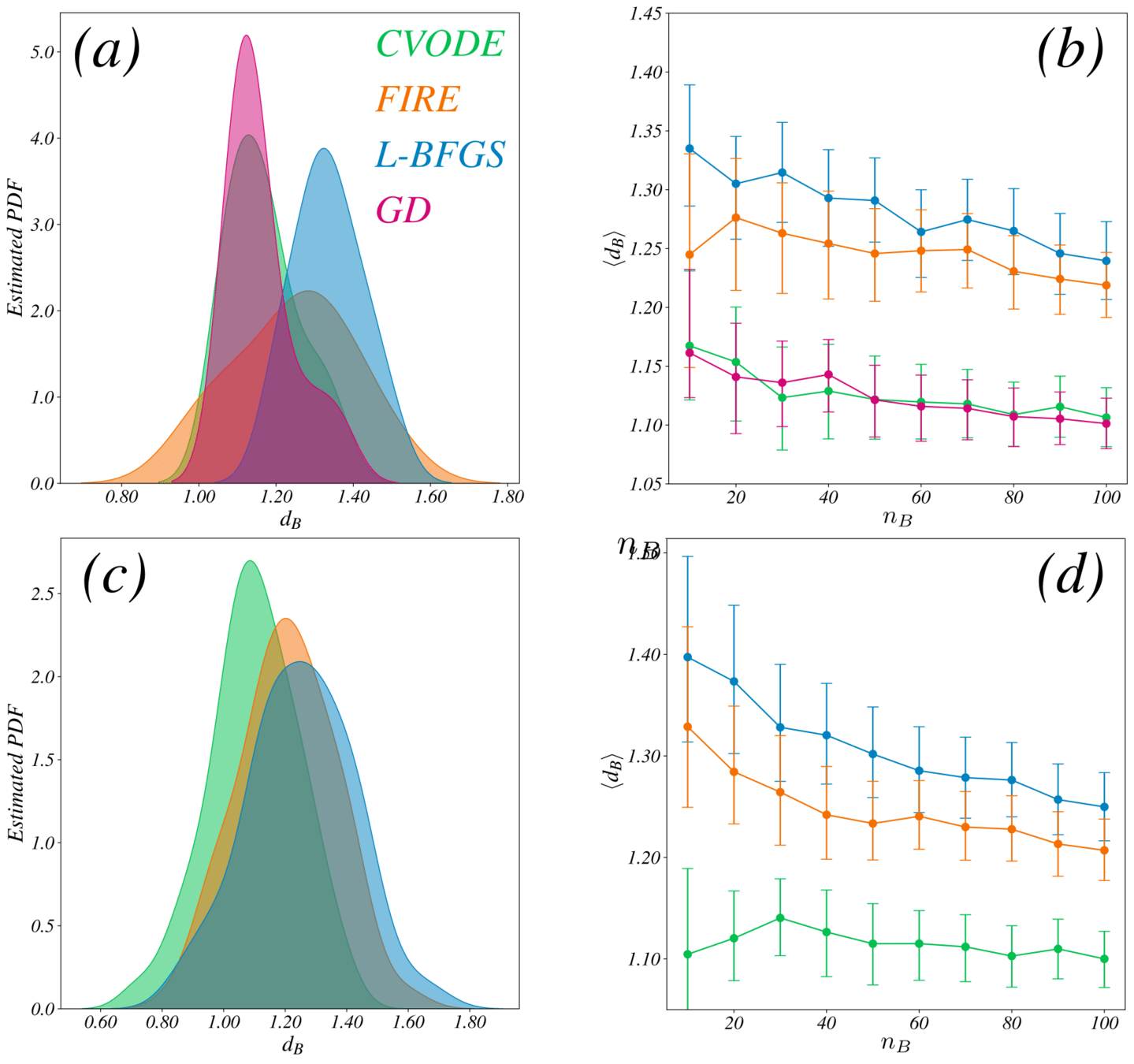
\(d_{L-BFGS} \sim 1.40\)

\(d_{FIRE} \sim 1.33\)
\(d_{CVODE} \sim 1.10\)
\(\phi=0.86\)
Limited by resolution!! Need multiple scales!! Can we do better?
Fractal dimension

\(d_{L-BFGS} \sim 1.40\)
\(d_{FIRE} \sim 1.33\)
\(d_{CVODE} \sim 1.10\)
Basins in high dimensions
Casiulis et al. Papers in Physics 15 (2023): 150001

Most Probable: Maximum radial density

Probability of landing inside the basin
Hypercube \(~1000d\)
Survival probability in a tentacle
Casiulis et al. Papers in Physics 15 (2023): 150001-150001.

Survival Probability at R: Probability of staying inside basin taking uniform samples at radius R
Initial state sensitivity

fraction of uncertain states
$$ f(R) \sim R^{\alpha}$$
$$ \alpha = D - d $$
\(D\) is dimension of phase space and \(d\) is box counting dimension of boundary
Scales as \(O(N^d)\)
Text
- Select a point at random in configuration space
- Define a random variable $$\mathbb{I}(R)$$ which is 1 if there is a boundary in the disc of radius \(R\) centered at the point and 0 if not
- define $$ f(R) = \left\langle \mathbb{I}(R) \right\rangle \propto R^\alpha$$
McDonald, S. W., Grebogi, C., Ott, E., & Yorke, J. A. (1985). Fractal basin boundaries. Physica D: Nonlinear Phenomena, 17(2), 125-153.
$$ \alpha = D - d $$
Where \(D\) is the full space dimension, and the \(d\) is the box counting dimension of the boundaries
Initial state sensitivity

fraction of uncertain states
$$ f(R) \sim R^{\alpha}$$
$$ \alpha = D - d $$
\(D\) is dimension of phase space and \(d\) is box counting dimension of boundary
Scales as \(O(N^d)\)
Text
McDonald, S. W., Grebogi, C., Ott, E., & Yorke, J. A. (1985). Fractal basin boundaries. Physica D: Nonlinear Phenomena, 17(2), 125-153.
To figure out whether there is a basin boundary in a disc in dimension \(D\) to precision \(\epsilon\), number of points to evaluate scales as \(\mathcal{O}(1/\epsilon^d)\) if we were to discretize the boundary of the disc
Initial state sensitivity

fraction of uncertain states
$$ f(R) \sim R^{\alpha}$$
$$ \alpha = D - d $$
\(D\) is dimension of phase space and \(d\) is box counting dimension of boundary
Scales as \(O(N^d)\)
Text
- Select a point at random in configuration space
- Define a random variable $$m(R)$$ which is the fraction of the boundary that belongs to the same basin
- define $$ P_{in}(R) = \left\langle \mathbb{I}(R) \right\rangle \propto R^{-\alpha}$$
$$ \alpha = D - d $$
Where \(D\) is the full space dimension, and the \(d\) is the fractal dimension of the basin around a random point
with some assumptions about there not being a characteristic length scale
Initial state sensitivity

fraction of uncertain states
$$ f(R) \sim R^{\alpha}$$
$$ \alpha = D - d $$
\(D\) is dimension of phase space and \(d\) is box counting dimension of boundary
Scales as \(O(N^d)\)
Text
To estimate \(P_{in}(R)\) with monte carlo to estimate the fraction to precision \(\epsilon\) number of points scale as \(\mathcal{O}(1/\epsilon^2)\)
Sierpinski carpet
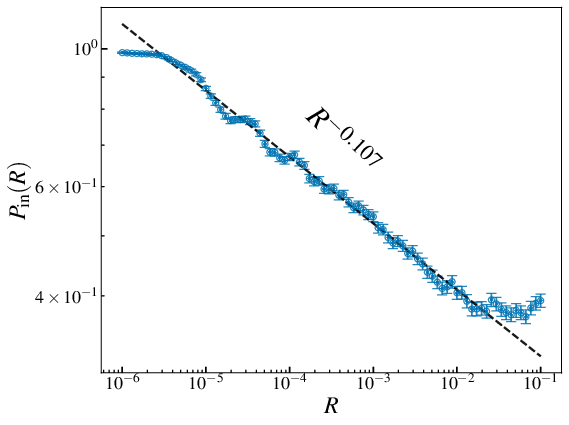
Predicts
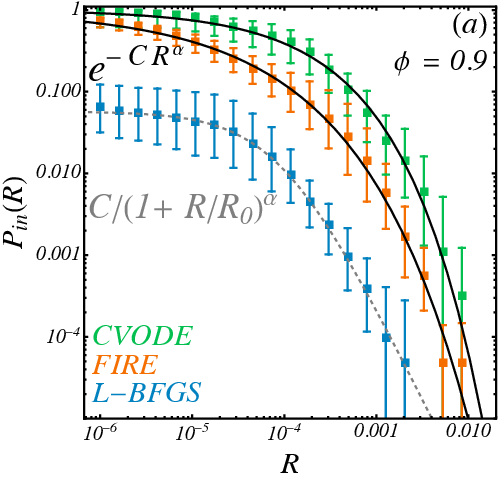
$$ P_{\mathrm{in}}(R) \sim R^{-0.107} $$

Survival probability in a tentacle
1024 particles
\(d_l=2046\)
Survival probability in a tentacle
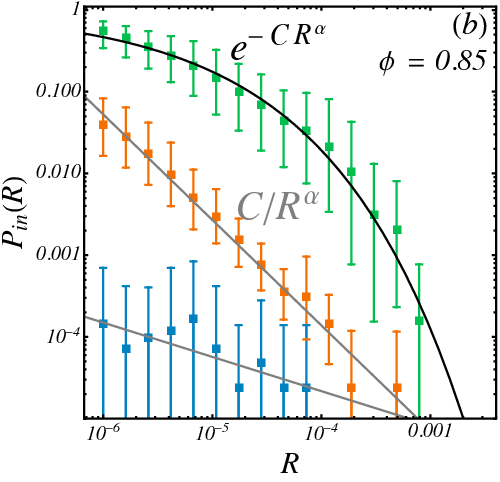
1024 particles
\(d_l=2046\)
Summary: geometry
- Basin boundaries are not fractal: Apparent fractality can emerge from using inadequate methods. This builds a case to re-verify previous geometric results that used optimizers.
- Qualitative and quantitative differences emerge as we get closer to jamming.
- Survival probability can estimate how "dust-like" a basin is in a dimension independent way
Roadmap
How do you identify a basin
Fractality/initial state sensitivity
Basin Volumes
High dimensional volumes
Basin Stability
Soft sphere packings
Wiley, D. A., Strogatz, S. H., & Girvan, M. (2006). The size of the sync basin. Chaos: An Interdisciplinary Journal of Nonlinear Science, 16(1).
Menck, P. J., Heitzig, J., Marwan, N., & Kurths, J. (2013). How basin stability complements the linear-stability paradigm. Nature physics, 9(2), 89-92.
Uses naive sampling.
Xu, N., Frenkel, D., & Liu, A. J. (2011). Direct determination of the size of basins of attraction of jammed solids. Physical Review Letters, 106(24), 245502.
Asenjo, Daniel, Fabien Paillusson, and Daan Frenkel. "Numerical calculation of granular entropy." Physical review letters 112.9 (2014): 098002.
Martiniani, S., Schrenk, K. J., Stevenson, J. D., Wales, D. J., & Frenkel, D. (2016). Structural analysis of high-dimensional basins of attraction. Physical Review E, 94(3), 031301.
Martiniani, S., Schrenk, K. J., Ramola, K., Chakraborty, B., & Frenkel, D. (2017). Numerical test of the Edwards conjecture shows that all packings are equally probable at jamming. Nature physics, 13(9), 848-851.
Uses optimizers. No guarantees that basins are not "dust-like"
Calculating volumes in high dimensions
Casiulis et al. Papers in Physics 15 (2023): 150001-150001.
$$Z(k) = \int_{\mathbb{R}^N}^{} \mathcal{O}(x) e^{- \frac{1}{2} k \left|x-x_{0}\right|^{2}} dx$$
Partition function
Oracle (1 if inside basin. 0 if outside)
Spring (to control exploration)
$$ F(k) = - log(Z_{k}) $$
Free energy
$$ F(0) - F(k_{\infty}) = \int_{0}^{k_{\infty}} \frac{\partial F}{\partial k} dk = \int_{k_{\infty}}^{0} \langle \left| x-x_{0}\right|^{2} \rangle_{k} dk$$
Log volume (unknown)
Spring free energy
Sampling basins in high dimensions
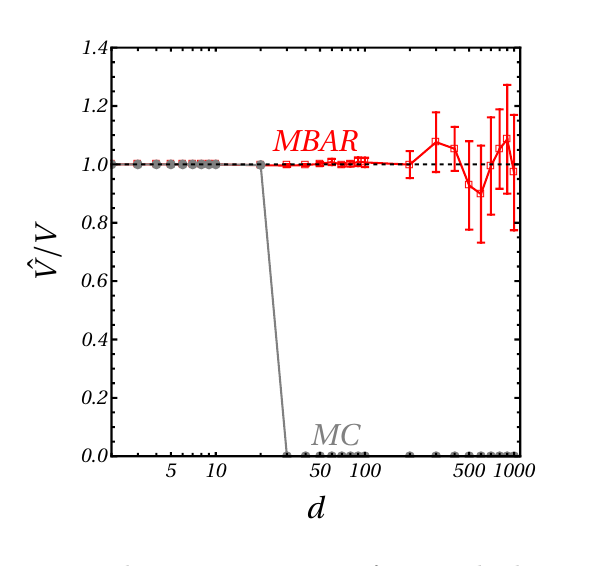
Brute force MC misses most of the volume!!
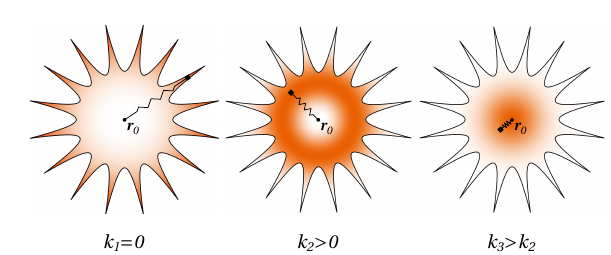
Reconstruct uniform samples from MC walkers at different distances, which can be used to constuct volumes
Casiulis et al. Papers in Physics 15 (2023): 150001-150001.
Replica exchange
Volumes of basins
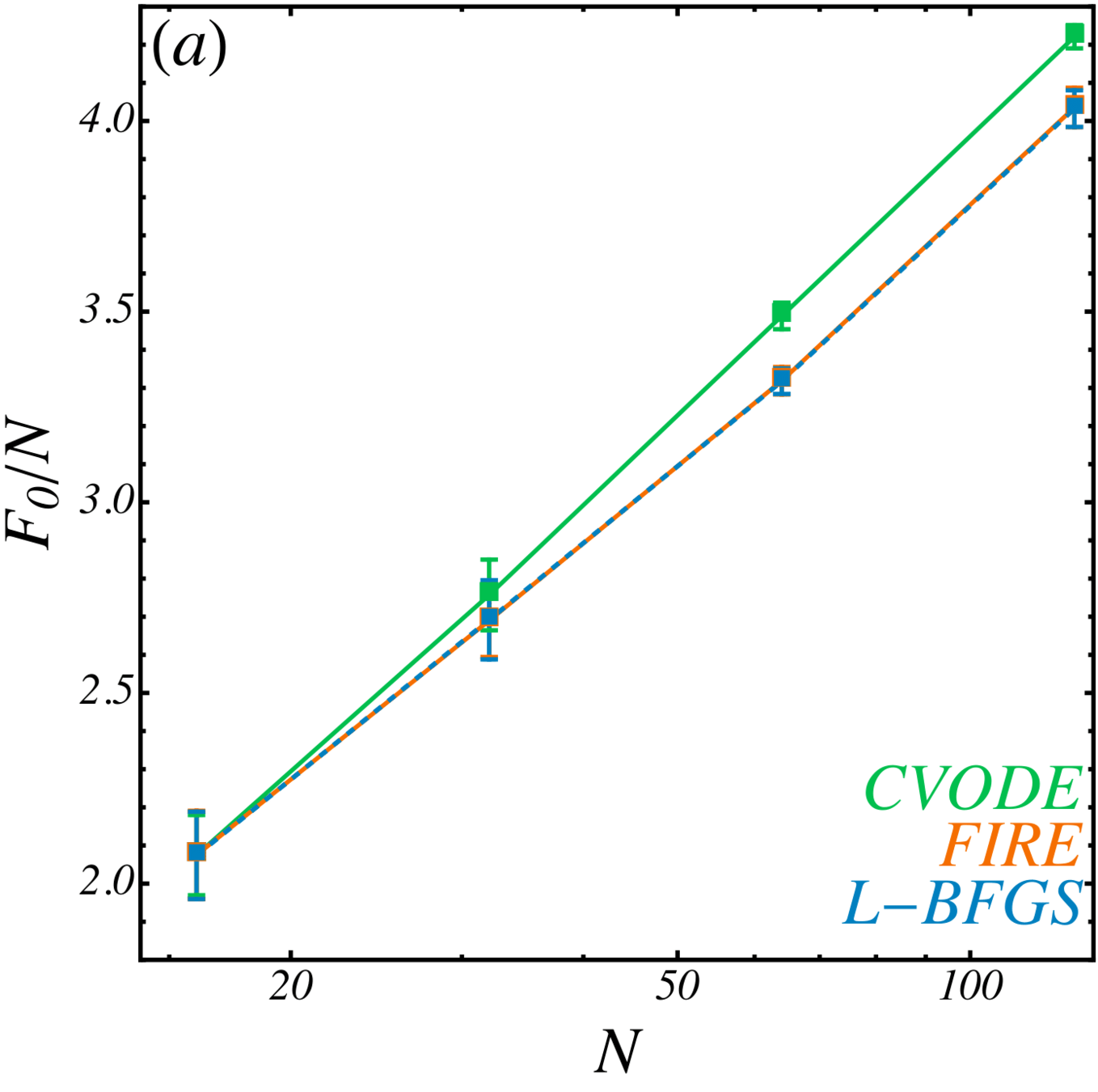
\(F_0 = - \ln V \)
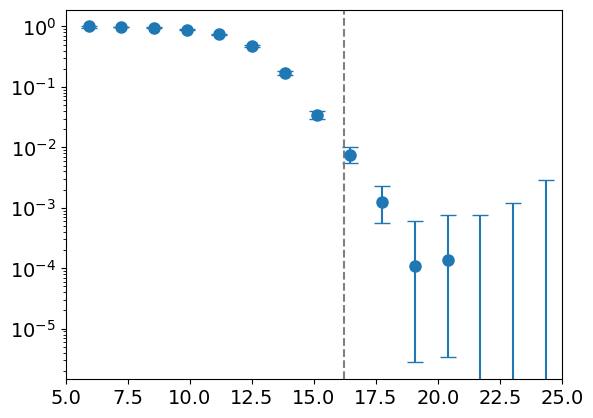
Accuracy within a single basin
\(128\) particles
\(d_l = 254 \)
Distance from minimum
Accuracy
Most basin volume
Distance from minimum
Radial Density of Basin
Optimizer accuracy
Density
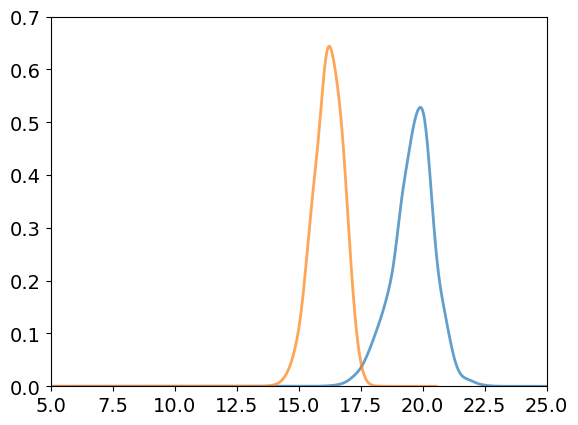
FIRE
CVODE
Take CVODE samples and minimize with FIRE
Accuracy within a single basin
\(128\) particles
\(d_l = 255 \)
Distance from minimum
Accuracy

Most basin volume
Distance from minimum
Radial Density of Basin
Optimizer accuracy
Density


FIRE
CVODE
Survival probability in a tentacle
Casiulis et al. Papers in Physics 15 (2023): 150001-150001.

Point lies at a distance \(r\)
Text
\(r\)
Survival probability in a tentacle
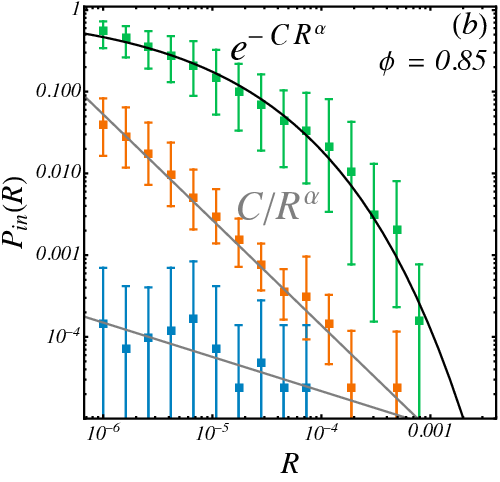
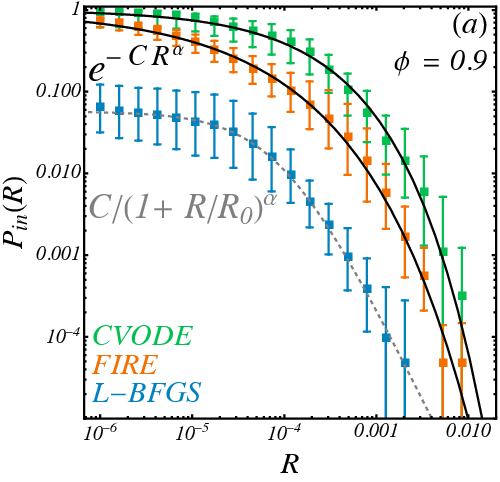
\(R_{1/2}\)
Survival probability in a tentacle
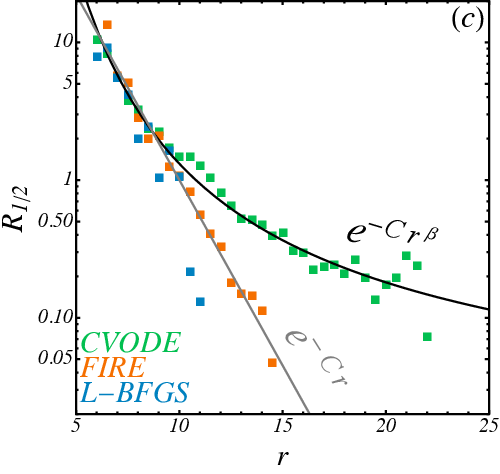
\(128\) particles
\(d_l = 254 \)
Summary
- First ODE based measurements hitting \(254d\) previously Xu.et al checked in \(14d\) for soft spheres.
- Optimizers (FIRE, L-BFGS) yield systematically larger volumes than CVODE, with bias growing with system size.
- Half-survival radius \(R_{1/2}(r)\) decays as simple exponential with optimizers (hypercube-like) but as stretched exponential with CVODE implying real basins have "thicker tentacles".
Counting by sampling
$$ N_{packings} = \frac{V_{space}}{\langle v_{basin} \rangle} $$
- Choose a random initial condition
- Let the system relax
Stable packings are minima of the potential

The Kauzmann paradox

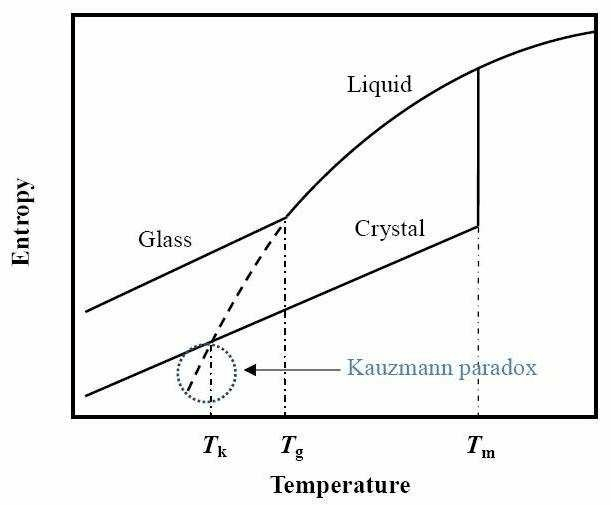
Entropy Decomposition
$$S_{\text{liquid}}(T) = S_{\text{conf}}(T) + S_{\text{vib}}(T)$$
One approach: Directly enumerate available configurations \(\Omega\) $$S_{\text{conf}} = k_B \ln \Omega$$
where \(\Omega\) = number of accessible configurations (inherent structures)
$$S_{\text{conf}} = 0 \implies \Omega = 1$$
Mapping inherent structures is important
Acknowledgments

Stefano Martiniani

Mathias Casiulis



Martiniani Lab

CVODE: Results
How to get Global Accuracy
- Generate \(N\) steepest descent trajectories to the minima at very low \(rtol\) from random initial conditions
- verify that the minima don't change when you increase \(rtol\) $$\frac{N_\text{incorrect}}{N} < 0.01 $$

\(N\)
\(rtol\)
95 percent accuracy
Accuracy curves: Harmonic potential (2d)

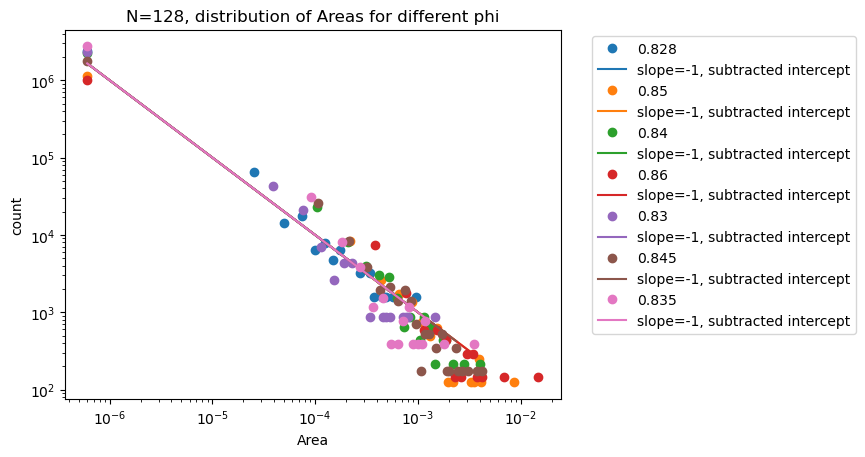
Areas

\(N=128\) \(d_l = 254\)
Polydisperse spheres
A fast and accurate algorithm
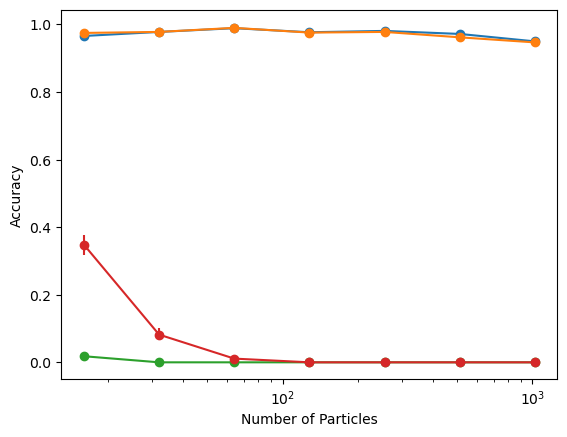
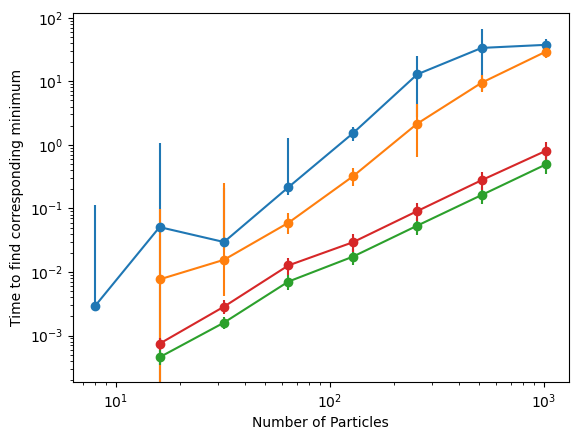
CVODE
Mixed Descent
FIRE
LBFGS
LBFGS
Mixed Descent
CVODE
FIRE
Counting by sampling
\(d\)
$$ N_{buildings} = \frac{D}{\langle\mathcal{d}\rangle} $$
Accuracy within a single basin
\(128\) particles
\(d_l = 14 \)
LBFGS
FIRE
Distance from minimum
Accuracy
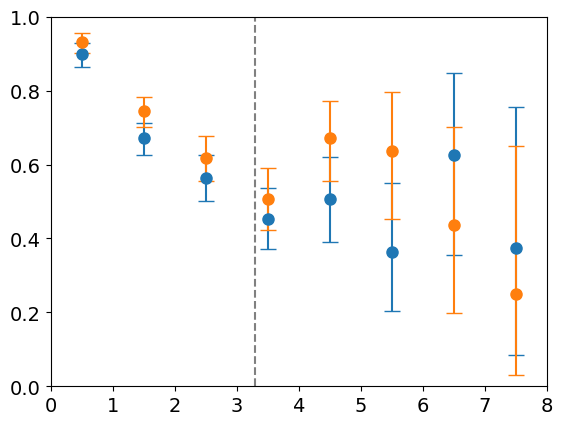
Most basin volume
Distance from minimum
Radial Density of Basin
Optimizer accuracy
Density