Book 2. Credit Risk

FRM Part 2

CR 4. Capital Structure in Banks

Presented by: Sudhanshu

Module 1. Expected and Unexpected Loss

Module 2. Economic Capital for Credit Risk

Module 1. Expected and Unexpected Loss

Topic 1. Credit Risk Factors

Topic 2. Expected Loss (EL)

Topic 3. Unexpected Loss (UL)

Topic 4. Portfolio Expected & Unexpected Loss

Topic 1. Credit Risk Factors

Definition of Credit Risk Factors: Credit risk is the possibility that a borrower will fail to meet obligations as agreed, resulting in financial loss to the lender.
The three most important factors in quantifying credit risk:
- Probability of Default (PD): Likelihood that the borrower defaults within a given horizon.
- Exposure at Default (EA/EAD): Dollar amount at risk at the time of default.
- Loss Rate (LR/LGD): Proportion of exposure lost if default occurs, with $L R = 1 - R eco v ery R a t e$ .
Probability of Default (PD) Definition: Statistical measure of likelihood that a counterparty defaults.
Interpretation: Even highly rated borrowers have non-zero PD.
Estimation Approaches:
- Historical default data (used by rating agencies).
- Structural models (e.g., Merton model → firm’s equity as call option on assets).
Example: A PD of 2% means that out of 100 similar loans, ~2 may default in a year.

Exposure at Default (EA/EAD) Definition: Amount the bank is exposed to if the borrower defaults.
Can be:
- Loan balance outstanding.
- Percentage of credit line drawn.
- Maximum facility amount available.
Importance: Determines the monetary scale of potential loss.
Example: Credit line = $5M, borrower draws $3M → EA = $3M.
Loss Rate / LGD Definition: Percentage of EA not recovered after default.
Formula:
$L R = 1 - RR$
where RR = recovery rate.
Drivers of LGD: collateral value, legal enforcement, seniority of claim.
Example: If $1M loan defaults and $400k is recovered → LGD = 60%.

Practice Questions: Q1

Q1. XYZ Bank is trying to forecast the expected loss on a loan to a mid-size corporate borrower. It determines that there will be a 75% loss if the borrower does not perform the financial obligation.

This risk measure is the:
A. probability of default.
B. loss rate.
C. unexpected loss.
D. exposure amount.

Practice Questions: Q1 Answer

Explanation: B is correct.

Current measures used to evaluate credit risk include the firm’s probability of default, which is the likelihood that a borrower will default, the loss rate, which represents the likely percentage loss if the borrower defaults, the exposure amount, and the expected loss, which, for a given time horizon, is calculated as the product of the EA, PD, and LR. The stated 75% loss if the borrower defaults is the loss rate.

Topic 2. Expected Loss (EL)

Definition Expected Loss (EL): The average or anticipated loss from a credit exposure over a time horizon.
Represents long-run statistical mean, not variability.
Formula & Components

$\times PD \times LR$

EA (Exposure at Default): $ amount at risk.
PD (Probability of Default): Likelihood of borrower default.
LR (Loss Rate): Severity of loss if default occurs.
Explanation
- EL represents what the bank expects to lose on average.
- Over many loans, EL smooths out actual defaults and recoveries.
- Banks hold reserves against EL, since it is a “planned-for” cost of lending.
Example (XYZ Bank)
- Loan outstanding: $1.8M.
- PD = 1%, LGD = 40%.
- EL = $1.8M \times 0.01 \times 0.40 = \$7,200$ .
- Interpretation: Over time, for many similar loans, average loss ≈ $7,200.

Topic 3. Unexpected Loss (UL)

Definition Unexpected Loss (UL): Potential deviation of actual loss from expected loss.
Captures risk of loss volatility due to uncertainty in defaults and recoveries.
Formula (Variance Based)

σ terms = variance (uncertainty) in PD and LR.
If σPD and σLR = 0 → UL = 0.
Explanation
- EL is predictable; UL is not.
- UL arises from:
  - Default risk: Even safe borrowers may default unexpectedly.
  - Credit migration: Rating downgrades increase default risk.
Example (XYZ Bank)
- EA = $1.8M, PD = 1%, LGD = 40%.
- σPD = 10%, σLR = 30%.
- UL = $90,000 (≈ 5% of EA).
- Interpretation: Losses can swing far above EL ($7,200).

U L = E A \times \sqrt{ \sigma_{P D}^{2} \cdot L R^{2} + \sigma_{L R}^{2} \cdot P D^{2} + \sigma_{P D}^{2} \cdot \sigma_{L R}^{2} }

Topic 4. Portfolio EL & UL

Portfolio EL
- Additive across assets.
- Straightforward aggregation of expected average losses.
Portfolio UL Formula
- Incorporates correlation among assets.
- Lower correlation → greater diversification → lower .
Risk Contribution
- Shows marginal risk from each asset.
- Ensures $\sum RC_i = UL_P$
Diversification & Correlation
- Diversifiable risk: firm-specific; cancels out in large portfolios.
- Undiversifiable risk: systematic; remains even in diversified portfolios.
- Example: With = 0.3, higher; with = 0.1, drops to $346k.

\sum R C_i=U L_P

U L_P

\rho

R C_i=\frac{\partial U L_P}{\partial U L_i}

UL_p

E L_P = \sum_{i=1}^{N} E L_i

\mathrm{UL}_{\mathrm{P}}=\sqrt{\sum_{\mathrm{i}} \sum_{\mathrm{j}} \rho_{\mathrm{ij}} \mathrm{UL}_{\mathrm{i}} \mathrm{UL}_{\mathrm{j}}}

Practice Questions: Q2

Q2. Which of the following statements about expected loss (EL) and unexpected loss (UL) is true?
A. Expected loss always exceeds unexpected loss.
B. Unexpected loss always exceeds expected loss.
C. EL and UL are parameterized by the exact same set of variables.
D. Expected loss is directly related to exposure.

Practice Questions: Q2 Answer

Explanation: D is correct.

EL increases with increases in the exposure amount. UL typically exceeds EL, but they are both equal to zero when probability of default is zero. UL has additional variance terms.

Practice Questions: Q3

Q3. If the recovery rate (RR) increases and the probability of default (PD) decreases, what will be the effect on expected loss (EL), all else equal?

Practice Questions: Q3 Answer

Explanation: D is correct.

If recovery rates increase, the loss rate will decrease, which will decrease expected loss. If the probability of default decreases, the expected loss will also decrease.

Practice Questions: Q4

Q4. Big Bank has contractually agreed to a $20,000,000 credit facility with Upstart Corp., of which $18,000,000 is currently outstanding. Upstart has very little collateral, so Big Bank estimates a one year probability of default of 2%. The collateral is unique to its industry with limited resale opportunities, so Big Bank assigns an 80% loss rate. The expected loss (EL) for Big Bank is closest to:
A. $68,000.
B. $72,000.
C. $272,000.
D. $288,000.

Practice Questions: Q4 Answer

Explanation: D is correct.

\begin{aligned} \mathrm{EL} & =\mathrm{EA} \times \mathrm{PD} \times \mathrm{LR} \\ & =\$ 18,000,000 \times 0.02 \times 0.8 \\ & =\$ 288,000 \end{aligned}

Practice Questions: Q5

Q5. Bigger Bank has two assets outstanding. The features of the loans are summarized in the following table. Assuming a correlation of 0.2 between the assets, what is the value of the unexpected loss of the portfolio

A. Less than $300,000.
B. Between $300,000 and $400,000.
C. Between $400,000 and $500,000.
D. Greater than $500,000.

\left(U L_p\right) ?

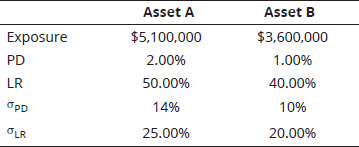
Practice Questions: Q5 Answer

Explanation: C is correct.

The following calculations describe the steps to compute the unexpected loss of a portfolio.
Compute UL for both assets.

Compute

\begin{aligned} \mathrm{UL} & =\mathrm{EA} \times \sqrt{\mathrm{PD} \times \sigma^2{ }_{\mathrm{LR}}+\mathrm{LR}^2 \times \sigma^2 \mathrm{PD}} \\ \mathrm{UL}_{\mathrm{A}} & =\$ 5,100,000 \times \sqrt{0.02 \times 0.25^2+0.5^2 \times 0.14^2}=\$ 399,952 \\ \mathrm{UL}_{\mathrm{B}} & =\$ 3,600,000 \times \sqrt{0.01 \times 0.2^2+0.4^2 \times 0.1^2}=\$ 160,997 \end{aligned}

\mathrm{UL}_p

\begin{aligned} \mathrm{UL}_{\mathrm{P}} & =\sqrt{(399,952)^2+(160,997)^2+(2)(0.2)(399,952)(160,997)} \\ & =\$ 460,041 \end{aligned}

Module 2. Economic Capital for Credit Risk

Topic 1. Economic Capital

Topic 2. Modeling Credit Risk

Topic 1. Economic Capital

Definition: Economic Capital (EC) is the capital held by bank to absorb unexpected losses at high confidence level (e.g., 99.97%).
Distinct from:
- Reserves: cover expected losses.
- Regulatory Capital: imposed by regulators.
Formula:
- CM = capital multiplier linked to confidence level.
- Ensures solvency even under extreme stress.
Explanation
- Represents “distance to default” — how much buffer exists.
- Higher UL → higher EC required.
- Aligns with desired credit rating and risk appetite.

E C_P=U L_P \times C M

Topic 2. Modeling Credit Risk

Credit Loss Distribution
- Not normal; typically skewed & fat-tailed.
- Limited upside (max = promised payments).
- Severe downside events (defaults) create tail risk.
Beta Distribution
- Defined on [0,1] → maps to loss rates 0–100%.
- Shape parameters (α, β) determine skewness.
- Mean = EL, variance = UL.
- Often combined with Monte Carlo to simulate tail losses.
Challenges in Quantifying Credit Risk
1. Illiquidity: Credit assets not traded in active markets.
2. Short horizon: Models often use 1-year horizon, ignoring longer cycles.
3. Siloed risk management: Credit, market, operational risks managed separately.
4. Correlation estimation: Very hard in large portfolios (e.g., 100 assets → 4,950 correlations).

Practice Questions: Q1

Q1. The type of capital used to buffer a bank from unexpected losses is known as:
A. economic capital.
B. regulatory capital.
C. unexpected capital.
D. risk-adjusted capital.

Practice Questions: Q1 Answer

Explanation: A is correct.

It is imperative that a bank hold capital reserves (i.e., economic capital) to buffer itself from unexpected losses so that it can absorb large losses and continue to operate.