Book 1. Market Risk

FRM Part 2

MR 4. Backtesting VaR

Presented by: Sudhanshu

Module 1. Backtesting VaR Models

Module 2. Conditional Coverage and Basel Backtesting Rules

Module 1. Backtesting VaR Models

Topic 1. Backtesting and Exceptions

Topic 2. Difficulties in Backtesting a VaR model

Topic 3. Using Failure Rates in Model Verification

Topic 4. Model Verification: Example

Topic 5. Type I and Type II Errors

Topic 6. Unconditional Coverage

Topic 7. Measuring Potential Losses Using VaR

Topic 1. Backtesting and Exceptions

Backtesting compares VaR model predictions to actual losses to validate model adequacy
Goal: ensure actual losses don't exceed expected losses at a given confidence level
Exceptions/exceedances: actual observations falling outside the VaR confidence level (should occur ≤1% at 99% confidence, ≤5% at 95% confidence)
Purpose: validates proper calibration and accuracy of VaR models for risk managers and regulators
Excessive exceptions trigger model recalibration and re-evaluation of assumptions/parameters
Basel Committee permits banks to use internal VaR models; backtesting ensures these models don't underestimate risk
Regulatory penalty: banks with >4 exceptions in 250 observations face higher capital requirements

Practice Questions: Q1

Q1. In backtesting a value at risk (VaR) model that was constructed using a 97.5% confidence level over a 252-day period, how many exceptions are forecasted?
A. 2.5.
B. 3.7.
C. 6.3.
D. 12.6.

Practice Questions: Q1 Answer

Explanation: C is correct.

(1 − 0.975) × 252 = 6.3

Topic 2. Difficulties in Backtesting a VaR Model

Portfolio mismatch: VaR assumes static portfolios, but actual compositions change constantly due to price movements and trading
Excluded factors: VaR models don't capture intraday changes, commissions, fees, interest income, and bid-ask spreads affecting actual P&L
Mitigation: use short time horizons (e.g., daily holding periods) to minimize these effects
Sample limitations: backtesting periods are limited samples that may not represent true underlying risk; predicted exception counts won't match exactly in every sample
Need for thresholds: requires establishing acceptable exception levels to determine when to reject models
Two-track approach: track both actual returns and hypothetical returns (assuming constant portfolio over holding period)
Cleaned returns: actual returns adjusted for non-market factors like funding costs and fee income; comparable to VaR model returns
Best practice: backtest both actual and hypothetical returns; adjust VaR methodology if hypothetical returns fail backtesting

Topic 3. Using Failure Rates in Model Verification

Failure Rate: Percentage of times VaR confidence level is exceeded; computed as N/T (exceptions ÷ sample size)
Basel requirement: banks must use 99% confidence level (p = 1% exception probability)
Probability of Exception ( $p$ ): The probability of exception, $p$ , is calculated as one minus the confidence level ( $p = 1 - c$ ).
Unbiased measure: probability of exception approaches the confidence level as the sample size increases.
Model Calibration Testing: Calculate z-score using formula using x (number of actual observations):
Decision rule: compare z-score to critical value (e.g., 1.96 for 95% confidence) to assess model calibration
Key distinction: the confidence level for testing model accuracy is separate from the VaR confidence level itself
Evaluation goal: determine if observed exceptions fall within expected range for a correctly calibrated model at chosen confidence level

z=\frac{x-pT}{\sqrt{p(1-p)T}}

Example: Suppose daily revenue fell below a predetermined VaR level (at the 95% confidence level) on 22 days during a 252-day period. Is this sample an unbiased sample?
Sol:
- Calculate z-score,
- Based on the calculation, this is not an unbiased sample because the computed z-value of 2.72 is larger than the 1.96 critical value at the 95% confidence level. In this case, we would reject the null hypothesis that the VaR model is unbiased and conclude that the maximum number of exceptions has been exceeded.

Topic 4. Model Verification: Example

z=\frac{x-pT}{\sqrt{p(1-p)T}} = \frac{22-0.05(252)}{\sqrt{0.05(0.05) 252}}=\frac{22-12.6}{\sqrt{11.07}}=\frac{0.4}{3.4598}=2.72

Practice Questions: Q2

Q2. A risk manager is backtesting a sample at the 95% confidence level to see if a VaR model needs to be recalibrated. He is using 252 daily returns for the sample and discovered 17 exceptions. What is the z-score for this sample when conducting VaR model verification?
A. 0.62.
B. 1.27.
C. 1.64.
D. 2.86.

Practice Questions: Q2 Answer

Explanation: B is correct.

The z-score is calculated using x = 17, p = 0.05, c = 0.95, and N = 252, as follows:

z=\frac{17-0.05(252)}{\sqrt{0.05(0.95) 252}}=\frac{17-12.6}{\sqrt{11.97}}=\frac{4.4}{3.4598}=1.27

Practice Questions: Q3

Q3. Which of the following statements regarding verification of a VaR model by examining its failure rates is false?
A. The frequency of exceptions can be determined with the confidence level used for the model.
B. According to Kupiec (1995), we should reject the hypothesis that the model is correct if the loglikelihood ratio (LR) > 3.84.
C. Backtesting VaR models with a higher probability of exceptions is difficult because the number of exceptions is not high enough to provide meaningful information.
D. The range for the number of exceptions must strike a balance between the chances of rejecting an accurate model (a Type I error) and the chances of failing to reject an inaccurate model (a Type II error).

Practice Questions: Q3 Answer

Explanation: C is correct.

Backtesting VaR models with a lower probability of exceptions is difficult because the number of exceptions is not high enough to provide meaningful information.

Topic 5. Type I and Type II Errors

Uncertainty in testing: samples cannot determine model accuracy with absolute certainty, only probability of observed exceptions
Error tradeoff: must balance Type I error (rejecting accurate model) vs. Type II error (accepting inaccurate model)
Backtesting goal: create VaR model with low Type I error and test for very low Type II error rate
Binomial distribution: establishes acceptable exception ranges at different confidence levels based on sample size
Basel requirements: 250 days of data at 99% confidence level (p = 0.01), yielding expected 2.5 exceptions
Regulatory penalty: banks face higher capital requirements with ≥5 exceptions
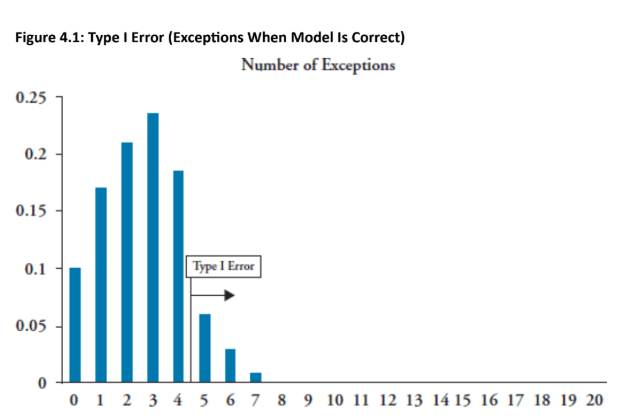
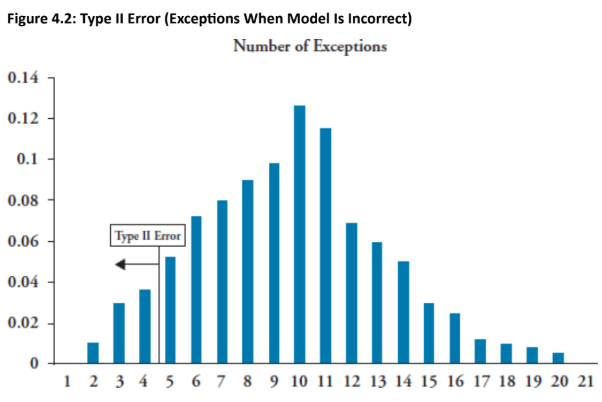
Type I error rate: 10.8% chance of observing ≥5 exceptions from a correct 99% VaR model (right tail rejection)
Type II error rate: 12.8% chance of failing to reject an incorrect model (97% confidence) when <5 exceptions occur (left tail)
Range determination: binomial probability distribution used to set acceptable exception thresholds at various confidence levels

Topic 5. Type I and Type II Errors

Topic 5. Unconditional Coverage

Definition: Unconditional coverage is a backtesting approach where the only concern is the total number of exceptions and not the timing or independence of their occurrence.
Kupiec's Log-Likelihood Ratio ( $L R_{u c}$ ): Kupiec (1995) developed a measure for accepting or rejecting models using the tail points of a log-likelihood ratio (LR). The test statistic for unconditional coverage ( $L R_{u c}$ ) is calculated as:

where $p$ is the probability level, $T$ is the sample size, and $N$ is the number of exceptions.
Rejection Criterion: The hypothesis that the model is correct is rejected if $L R_{u c} > 3.84$ . This critical value of 3.84 corresponds to a chi-squared test statistic at a 95% confidence level (with one degree of freedom, assuming a large sample $T$ ).
- Note: 3.84 is the square of the normal distribution test statistic of 1.96 at the 95% confidence level.

LR_{uc}=-2ln[(1-p)^{T-N}p^N]+2ln{[1-(N/T)]^{T-N}(N/T)^N}

Practice Questions: Q4

Q4. Unconditional testing does not reflect the:
A. size of the portfolio.
B. number of exceptions.
C. confidence level chosen.
D. timing of the exceptions.

Practice Questions: Q4 Answer

Explanation: D is correct.

Unconditional testing does not capture the timing of exceptions.

Topic 6. Measuring Potential Losses Using VaR

VaR purpose: measure potential losses over a specific time period
Theory 1 (Liquidity-based): holding period = time required to liquidate or hedge portfolio before corrective action
Theory 2 (Stability-based): holding period = time portfolio remains unchanged due to non-risk activity (e.g., trading)
Practical similarity: both theories often yield similar holding periods
Banking practice: many banks use daily VaR aligned with daily P&L measurement
Key insight: holding period selection is more significant than confidence level choice for this application

Module 2. Conditional Coverage and Basel Backtesting Rules

Topic 1. Conditional Coverage

Topic 2. Basel Committee Rules for Backtesting

Topic 1. Conditional Coverage

The concept of conditional coverage extends the backtesting framework beyond simply counting the number of exceptions.
Need for Conditional Coverage:
- The examples and discussion of backtesting often focus on
  
  unconditional coverage, which does not consider the timing of exceptions.
- Conditional coverage incorporates the time variation of the data.
- In an accurate model, exceptions are anticipated to be fairly equally distributed across time.
- A "bunching" or clustering of exceptions may indicate that market correlations have changed or that trading positions have been altered.
- If exceptions are found to be non-independent (serially dependent), the risk manager should incorporate models that consider time variation in risk.
- Conditional coverage is required to determine if the clustering of exceptions is random or caused by model or trading changes.

Christoffersen's Test:
- Christoffersen extended the unconditional coverage test statistic ( $L R_{u c}$ ) to account for potential time variation in the data.
- He developed a log-likelihood ratio test statistic for the serial independence of deviations ( $L R_{in d}$ ).
- The overall log-likelihood test statistic for conditional coverage ( $L R_{cc}$ ) is computed as the sum of the unconditional coverage test and the independence test:
  
  $L R_{cc} = L R_{u c} + L R_{in d}$
- Each component ( $L R_{u c}$ and $L R_{in d}$ ) is independently distributed as chi-squared, and their sum is also distributed as chi-squared.
- Rejection Criteria (at the 95% confidence level):
  - Reject the model if $L R_{cc} > 5.99$ .
  - Reject the independence assumption if $L R_{in d} > 3.84$ .

Topic 2. Basel Committee Rules for Backtesting

The Basel Committee has established rules for backtesting internal VaR models, primarily concerned with striking a balance between Type I and Type II errors.
Requirements:
- Market VaR must be calculated at the 99% confidence level.
- It must be backtested over the past year, which is approximately 250 trading days.
- At the 99% confidence level, the expected number of exceptions is
  
  $250 \times 0.01 = 2.5$ exceptions per year.
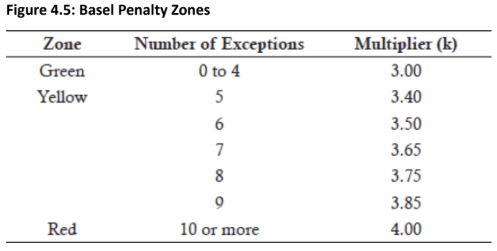
Basel Penalty Zones:
- The Committee designed penalty zones to mitigate the risk that banks deliberately commit a Type II error (using a faulty model).
- Banks are penalized for exceeding four exceptions per year.
- The penalty is an incremental increase in the capital multiplier ( $k$ ), which normally starts at 3.00.
- Increasing $k$ significantly increases the bank's required capital and lowers performance measures like return on equity.

Practice Questions: Q1

Q1. The Basel Committee has established four categories of causes for exceptions. Which of the following does not apply to one of those categories?
A. The sample is small.
B. Intraday trading activity.
C. Model accuracy needs improvement.
D. The basic integrity of the model is lacking.

Practice Questions: Q1 Answer

Explanation: A is correct.

Causes include the following: bad luck, intraday trading activity, model accuracy needs improvement, and the basic integrity of the model is lacking.