Book 3. Operational Risk

FRM Part 2

OR 21. Capital Regulation Before the Global Financial Crisis

Presented by: Sudhanshu

Module 1. Basel I Regulations and Revisions

Module 2. Basel II Regulations

Module 1. Basel I Regulations and Revisions

Topic 1. Overview
Topic 2. Need for Basel Regulations

Topic 3. BCBS Creation

Topic 4. Capital and Risk-Weighted Assets

Topic 5. Two Capital Compoments

Topic 6. RWAs for On-Balance-Sheet Items

Topic 7. RWAs for Off-Balance Sheet Items

Topic 8. Credit Exposure Method

Topic 9. Original Exposure Method

Topic 10. 1995 Amendment: Netting

Topic 11. 1996 Amendment: Market Risk and Trading Activities

Topic 12. 1996 Amendment: SA and IMA

Topic 13. 1996 Amendment: MR VaR (IMA)

Topic 14. 1996 Amendment: Backtesting

Topic 1. Overview

  • Basel I (1988) introduced the first risk-weighting system for bank activities and established capital-to-risk-weighted assets requirements, but only addressed credit risk
  • Basel II expanded risk measurement to include credit risk, market risk, and operational risk using more sophisticated approaches than Basel I
  • Key exam focus areas include understanding Basel II's contributions to risk measurement and knowing differences between various risk calculation methods
  • Important to distinguish between Basel II (banking standards) and Solvency II (similar international standards for insurance companies)
  • Students must understand potential repercussions firms face when breaching Basel standards and be able to calculate required capital under various regulatory regimes
  • Recurring theme involves contrast between standardized approaches (used by less sophisticated institutions) and internal approaches (firm-specific and more complex)
  • Internal approaches often result in lower required capital because they allow banks to use proprietary model inputs and account for asset correlations
  • Advanced internal methods provide more risk-sensitive capital requirements but require greater regulatory approval and sophisticated risk management capabilities

Topic 2. Need for Basel Regulations 

  • Early banks signaled financial soundness through large capital reserves and impressive buildings to build depositor confidence
  • Initial regulations came from private initiatives like the Bank of England and clearinghouses that provided mutual monitoring through shared financial statements
  • Current regulatory frameworks emerged when private sector monitoring proved insufficient to prevent systemic banking failures
    • ​Banking panics created unmanageable runs and losses, requiring government-backed central banks with money-printing power as "lenders of last resort"
    • Governments recognized financial crises caused recessions and depressions, motivating efforts to ensure financial system solvency and liquidity
    • Failed bank customers complained about difficulty assessing bank safety, highlighting need for better regulatory oversight and transparency
    • International trade expansion in the 1960s-1970s increased importance of coordinated global banking regulations
      • ​Large international financial institutions created global systemic risk where failures could affect multiple countries simultaneously
      • Banks in countries with lenient regulations gained competitive advantages over those with strict capital requirements, creating regulatory arbitrage
      • Globalization caused settlement complexities from time zone and currency differences, leading to clearing failures like Herstatt Bank's 1974 collapse

Topic 3. BCBS Creation

  • Basel Committee on Banking Supervision (BCBS) was created in 1974, comprising roughly the Group of Ten (G10) nations
  • Pre-1988 bank capital regulations were inconsistent across countries and ignored individual bank risk profiles, using simple capital-to-assets or assets-to-capital ratios
  • Enforcement varied significantly between countries and regulatory authorities, creating uneven competitive conditions
  • Growing complexity in off-balance sheet OTC derivatives (interest rate swaps, currency swaps, options) bypassed capital requirements since they didn't affect total assets
  • Bank balance sheets varied significantly in risk composition, reinforcing the belief that total assets poorly reflected actual bank risk
  • Basel I (1988 BIS Accord) established first international risk-based capital adequacy standards, though lacking legal authority over financial institutions
  • Countries adopted Basel I standards through domestic laws and regulations rather than direct international enforcement

Topic 4. Capital and Risk-Weighted Assets

  • Basel I's key innovation was risk-weighting bank assets rather than focusing solely on capital relative to total assets. Basel I required three capital requirements:
    • Total Assets-to-Capital Ratio: Banks required capital-to-total-assets ratio greater than 5% (assets-to-capital ratio less than 20), similar to pre-1988 requirements
    • Tier 1 Capital Requirement: Tier 1 capital to risk-weighted assets (RWAs) must exceed 4%, with RWAs calculated from on- and off-balance sheet items to measure total credit exposure
    • Total Capital Requirement: Combined Tier 1 and Tier 2 capital to RWAs must exceed 8%, known as Cooke ratios. Tier 2 capital capped at maximum 50% of total capital, with excess Tier 1 capital above 4% counting toward total capital requirement

Topic 5. Two Capital Components

  • Basel I defined the two components of capital as follows:

    • Tier 1 capital (or core capital) consists of:

      • ​Equity (subtract goodwill from equity).

      • Noncumulative perpetual preferred stock.

    • Tier 2 capital (or supplementary capital) consists of:

      • ​Cumulative perpetual preferred stock.

      • Certain types of 99-year debentures.

      • Subordinated debt with an original maturity greater than five years (where the subordination is to depositors).

  • Tier 1 (equity) capital absorbs losses while Tier 2 (supplementary) capital is subordinate to depositors, protecting them during bank failure
  • Minimum 50% of total capital must be Tier 1, with half of Tier 1 requirement met through common equity
  • Some countries imposed capital requirements above Basel I minimums

Topic 6. RWAs for On-Balance-Sheet Items

  • Risk-weighted assets (RWAs) are calculated by assigning risk weights to each on-balance sheet and off-balance sheet item that reflect the bank's credit risk exposure to those assets

  • A sample of some of the risk weights assigned to various asset categories is shown in Figure 62.1.

  • RWAs are calculated by multiplying the on-balance sheet amount of the item by the percentage risk weight and summing the products.

  • Example: The assets of Blue Star Bank consist of $20million in U.S. Treasury bills, $20 million in insured mortgages, $50million in uninsured mortgages, and $150million in corporate loans. Using the risk weights from Figure 62.1, calculate the bank’s risk-weighted assets.

    • ​Solution:

\text{RWAs } = (0.0 \times \$ 20)+(0.0 \times \$ 20)+(0.5 \times \$ 50)+(1.0 \times \$ 150)=\$ \text{175 million}

Topic 7. RWAs for Off-Balance-Sheet Items

  • Credit Equivalent Amounts (CEAs): Off-balance sheet items are converted to CEAs using regulator-prescribed measures to quantify credit risk for capital calculation purposes
  • Banks "convert" off-balance sheet items into on-balance sheet equivalents, then multiply by risk weights to arrive at risk-weighted values
  • Conversion factors vary by instrument type: loan-like items (e.g., banker's acceptances) use 100% conversion factors while others like note issuance facilities have lower factors
  • For derivatives, CEA measures are applied, while non-derivatives use conversion factors applied to the principal amount​:
  • Example: A $200 million standby letter of credit to a government agency would first be converted to a $100million credit equivalent (= $200million*0.50) then would be assigned a 20% risk weight. It would thus contribute $20 million to RWA.

  • For IRS and other OTC derivatives, regulators may choose between the current exposure method and the original exposure method.

Topic 8. Current Exposure Method

  • For the current exposure method, the credit equivalent amount is calculated as:

    • ​

    • where

      • ​V: current value of the derivative of the market

      • D: add-on factor (to account for changes in the contract's future market market)

      • L: principal amount

  • Current Exposure Component [max(V, 0)]: Represents bank's immediate loss if counterparty defaults - positive derivative value V creates exposure, while negative value creates no exposure
  • Add-on Amount (D × L): Accounts for potential future increases in bank's exposure over the derivative's remaining life
  • Risk-Based Add-on Factors: Higher factors applied to riskier derivatives with longer maturities and riskier underlying assets, as shown in below figure:
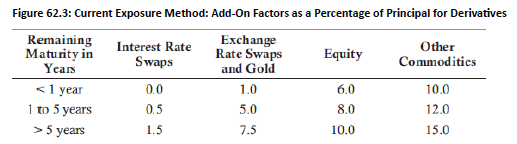
\text{RWAs } = \max (\mathrm{V}, 0)+\mathrm{D} \times \mathrm{L}

Topic 8. Current Exposure Method

  • Example (CEA for off-balance sheet items): Blue Star Bank has entered a $175 million IRS with a remaining maturity of three years. The current value of the swap is $2.5 million. Calculate the swap’s CEA.
    • ​Solution: The add-on factor is 0.5% of the IRS principal.
  • ​The nature of the counterparty determines risk weights. CEA is multiplied by the counterparty risk weight to calculate risk-weighted assets. Risk weights are shown in Figure 62.1.
  • Example (RWAs for off-balance sheet items): Blue Star Bank entered an IRS that had a CEA of $3,375,000. Calculate the RWAs assuming (1) counterparty is an OECD bank and (2) the counterparty is a corporation.
    • RWA assuming counterparty is an OECD bank:
    • RWA assuming counterparty is a corporation:​
  • ​The total RWAs of the bank are calculated by summing the on- and off-balance sheet risk-weighted items:
  •  
    • ​where
      • ​
      •  
      •  
  • ​The bank must maintain at least 8% capital to RWA.
  • Example (risk-based capital): Using the information from the previous three examples, calculate Blue Star Bank’s required capital, assuming the swap counterparty is a corporation.
    • ​
\text{CEA } =\$ 2.5+(0.005 \times \$ 175)=\$ \text{ 3.375 million}
\text{RWA } =\$ 3,375,000 \times 0.2=\$ 675,000
\text{RWA } =\$ 3,375,000 \times 1.0=\$ 3,375,000
\text{Total RWA }=\sum_{i=1}^N w_i L_i+\sum_{j=1}^M w_j C_j
w_i \text{ and } w_j \text{ are risk-weights of the counterparty for on- and off-balance sheet items}
L_i \text{ is the principal of the i-th on-balance sheet item}
C_j \text{ is CEA of the j-th off-balance sheet item}
\text{Required Capital } =(\$ \text{ 175 million} +\$ \text{ 3.375 million} ) \times 0.08=\$ \text{ 14.27 million}

Practice Questions: Q1

Q1. Michigan One Bank and Trust has entered a $200 million interest rate swap with a corporation. The remaining maturity of the swap is six years. The current value of the swap is $3.5 million. Using the
table below to find the add-on factor for the interest rate swap, the equivalent risk-weighted asset (RWA) under Basel I is closest to:
 

 

 

 


A. $3,000,000.
B. $3,250,000.
C. $3,500,000.
D. $6,500,000.

Practice Questions: Q1 Answer

Explanation: B is correct.

The add-on factor is 1.5% of the interest rate swap principal for swaps with a maturity greater than five years.

 

 

 

 

 

The risk-weight factor for a corporate counterparty under Basel I is 100% for corporate loans.

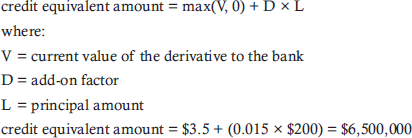
  • The original exposure method is only allowed for interest rate and foreign exchange contracts.
  • For the original exposure method, nations may ignore current market values and choose to use either the original or remaining maturity of the derivative.

  • For banks choosing the original exposure method, a sample of add-on factors is shown in Figure 62.4.

Topic 9. Original Exposure Method

Topic 10. 1995 Amendment: Netting

  • The original Basel I disincentivized hedging by requiring a capital charge on each side of offsetting positions.

  • Netting: The ISDA master agreement allowed for positive and negative values to offset one another, called netting.

  • Netting is frequently employed in transactions that generate credit exposure to both sides.

  • With netting, if a counterparty defaults, the bank only loses the net amount of all transactions, not the sum of all positive exposures.

  • The 1995 amendment allowed for a reduction in the CEA by putting a legal netting agreement was in place.

  • The Net Replacement Ratio (NRR) was introduced to measure the impact of netting:

    •  

  • The CEA formula was modified to include the NRR, reducing the RWA

    •  

    •  

  • In calculating CEAs, the complete netting of market positions is allowed and add-ons are reduced for each category.

NRR=\frac{\text{Current exposure with netting}}{\text{Current exposure without netting}}
\text{CEA }=\max \left(\sum_{i=1}^N V_i, 0\right)+\sum_j\left[0.4 \times D_j+0.6 \times D_j \times N R R\right]

Topic 11. 1996 Amendment: Market Risk and Trading Activities

  • The 1995 amendment did not fully capture market risk, which is the risk associated with changes in the market values of trading book assets.

  • The 1996 amendment required banks to measure and hold capital for these risks.

  • Trading Book: Banks must mark-to-market (i.e., fair value accounting) those instruments that are held by the bank for the purpose of trading. These include bonds, marketable equity securities, commodities, foreign currencies, and most derivatives.

  • Banking Book:  Banks do not have to use fair value accounting on assets they intend to hold for investment purposes. This includes loans and some debt securities.

  • The 1996 Amendment proposed two methods for calculating market risk:

    • Standardized Measurement Method (SA)

    • Internal Model-Based Approach (IMA)

  • ​Under both approaches, for each of the five categories, capital charges were calculated separately for specifiic risk (SR) and general market risk (MR).

Topic 12. 1996 Amendment: SA and IMA

  • Standardized Measurement Method:
    • Assigns separate capital charges to each trading book item, ignoring correlations between instruments,
    • Typically used by banks with less sophisticated risk management
  • Internal Model-Based Approach:
    • Allows banks to develop internal risk measures using regulator-specified formulas, contrasting with standardized approach that relies on observable characteristics like remaining maturity
    • VaR-Based Capital Calculation: Internal method uses specified formulas to calculate value at risk (VaR) measures and convert them into capital requirements
    • Lower Capital Through Diversification: Internal approach generally produces lower capital charges by accounting for correlations and diversification benefits between instruments,
    • Preferred by banks with advanced risk management capabilities

    • Risks covered by the VaR model include movements in broadmarket variables such as interest rates, exchange rates, stock market indices, and commodity prices.

    • The VaR model does not incorporate company-specific risks such as changes in a firm’s credit spread or changes in a company’s stock price. The SR charge captures these company-specific risks.

    • For example, a corporate bond has interest rate risk, captured by VaR, and credit risk, captured by the SR.

  • Note: The 1996 Amendment created Tier 3 capital, consisting of short-term subordinated, unsecured debt with an original maturity of at least two years. It could be used to meet the market risk capital requirement. Tier 3 capital has subsequently been eliminated under Basel III.

  • VaR parameters: 10-day time horizon, 99% confidence level.

  • MR VaR= max(VaRt−1​, m×VaRavg​)

    • VaRt−1​ = previous day's VaR.

    • VaRavg​ = average VaR over the last 60 trading days.

    • m = multiplicative factor (at least 3, can be higher if the model has deficiencies).

  • Banks calculate a 10-day 99% VaR for SR. Regulators then apply a multiplicative factor (which must be at least four) to determine the capital requirement.

  • The total capital requirement for banks using IMA must be at least 50% of the capital required using SA.

  • The amendment also introduced a separate charge for specific risk (SR) to capture company-specific risks (e.g., changes in a firm's credit spread).

  • Total capital charge (1996 Amendment): Sum of Basel I credit risk capital and the new market risk capital. For simplicity, the RWAs for market risk capital was defined as 12.5 times the MR VaR.

    • Total Capital=0.08×(credit risk RWA+market risk RWA)

    • Market RWA=12.5×[max(VaRt−1​,m×VaRavg​)]

    •  

  • Example: MR Capital Charge

    • Previous day's VaR = $10 million, Average VaR over 62 days = $8 million., Multiplicative factor = 3.

    • MR Capital Charge = 0.08 × Market RWA = 0.08×[12.5×(3×$8 million)]=$24 million.

\text{Credit RWA } =\Sigma \text{(RWA on-balance sheet) } +\Sigma \text{(RWA off-balance sheet)}

Topic 13. 1996 Amendment: MR VaR (IMA)

  • Backtesting Requirement: Banks must backtest their one-day 99% VaR against actual losses over the previous 250 trading days
  • Exception Recording Process: Banks calculate VaR for each of the 250 days using current methods and compare to actual losses, recording exceptions when actual losses exceed VaR estimates
  • Multiplicative Factor (m) Setting: m is determined based on the total number of exceptions recorded over the 250-day period
  • Performance-Based Penalties: Higher exception counts result in increased multiplicative factors, effectively penalizing banks with less accurate VaR models

  • If, over the previous 250 days, the number of exceptions is:

    • ​less than 5,m is usually set equal to 3.

    • 5, 6, 7, 8, or 9,m is set equal to 3.4, 3.5, 3.65, 3.75, and 3.85, respectively.

    • greater than 10,m is set equal to 4.

  • The bank supervisor has discretion regarding the multiplier.
    • Position Change Exceptions: Higher multipliers may or may not be applied when exceptions result from changes in bank positions during the trading day
    • Model Deficiency Exceptions: Higher multipliers are likely applied when exceptions stem from deficiencies in the bank's VaR model
    • Bad Luck Exceptions: No specific guidance exists for supervisors regarding higher multipliers when exceptions are simply due to random market movements

Topic 14. 1996 Amendment: Backtesting

Practice Questions: Q2

Q2. Saugatuck National Bank uses the internal model-based approach to set market risk capital as prescribed by the 1996 Amendment to the 1988 Basel Accord. The bank has backtested its 99% one-day VaRs against the actual losses over the last 250 trading days. Based on the results of the backtesting, the bank recorded 11 exceptions. Based on these results, the multiplicative factor (m)
in the model should be set:
A. less than 3.
B. equal to 3.
C. between 3.1 and 3.9.

D. equal to 4.

Practice Questions: Q2 Answer

Explanation: D is correct.

Saugatuck National Bank must compare the VaR calculated using its current method for each of the 250 trading days to the actual loss over the same period to determine the multiplicative factor. If the actual loss is greater than the estimated loss, an exception is recorded. If, over the previous 250 days, the number of
exceptions is:

  • less than 5,       is usually set equal to three.
  • 5, 6, 7, 8, or 9,      is set equal to 3.4, 3.5, 3.65, 3.75, and 3.85, respectively.
  • greater than 10,       is set equal to four.

Therefore, with 11 exceptions recorded,       should be set equal to four.

m_c
m_c
m_c
m_c

Module 2. Basel II Regulations

Topic 1. Basel II Overview

Topic 2. Basel II Pillar 1: Minimum Capital Requirements

Topic 3. Basel II Pillar 2: Supervisory Review

Topic 4. Credit Risk Capital Requirements

Topic 5. Credit Risk Capital Requirements

Topic 6. CR Capital Requirements: Standardized Approach

Topic 7. CR Capital Requirements: Internal Ratings-Based (IRB) Approach

Topic 8. CR Capital Requirements: Advance IRB Approach

Topic 9. CR Capital Requirements: Foundation and Advance IRB Approaches for Retail Exposures

Topic 10. Operational Risk Capital Requirements

Topic 11. Solvency II Framework

Topic 1. Basel II Overview

  • Basel I Limitations: Treated all corporate loans equally with 100% risk weight regardless of creditworthiness (AAA-rated same as C-rated borrower) and ignored diversification benefits
  • Basel II Development: Proposed June 1999, published 2004, implemented 2007 to correct Basel I deficiencies, applying to "internationally active" banks
  • Regional Bank Exception: Many small U.S. regional banks remained under Basel IA (similar to Basel I) while all European banks adopted Basel II
  • Three Pillar Structure: Basel II established three pillars structure:
    • Minimum capital requirements,
    • Supervisory review, and
    • Market discipline as core framework components
  • ​To summarize, Basel II contained four important innovations:
    • ​More sophisticated risk weight formulas based on the internal risk measures of banks andmodern concepts of credit risk management.
    • Required capital for operational risk, in addition to credit and market risks.
    • Specific requirements for supervision related to capital (Pillar 2) and improved transparency as a result of greater bank disclosures (Pillar 3).
    • Use of QIS to improve the Basel II Accord.

Topic 2. Basel II Pillar 1: Minimum Capital Requirements

  • The key element of Basel II regarding capital requirements is to consider the credit ratings of counterparties.

  • Capital charges for market risk remained unchanged from the 1996 Amendment. Basel II added capital charges for operational risk.

  • Banks must hold total capital equal to 8% of RWA under Basel II, as under Basel I.

  • Total capital under Basel II is calculated as:

    • ​

\text{Total Capital } =0.08 \times\text{(Credit Risk RWA + Market Risk RWA + Operational Risk RWA)}

Topic 3. Basel II Pillar 2: Supervisory Review

  • Global Consistency Goal: Basel II aims to achieve overall consistency in capital requirements for internationally active banks worldwide
  • Regulatory Discretion: Pillar 2 allows national regulators flexibility to consider local conditions when implementing Basel II rules
  • Enhanced Risk Management: Supervisors must encourage banks to develop better risk management functions and evaluate risks beyond Pillar 1 scope
  • Internal Assessment Requirement: Banks required to establish internal capital adequacy and assessment processes (ICAAP) that account for their specific risk profiles

Topic 4. Basel II Pillar 2: Market Discipline

  • The goal of Pillar 3 is to increase transparency. Banks are required to disclose more information about the risks they take and the capital allocated to these risks.

  • Qualitative disclosures such as the bank’s corporate structure and quantitative disclosures, such as the bank’s capital, risk exposures, and risk measures, were required.

  • The key idea behind Pillar 3 is that if banks must share more information with shareholders (and potential shareholders), they will make better risk management decisions.

  • Banks have discretion in determining what is relevant and material and thus what should be disclosed. Also, using data provided by banks, supervisors fine-tuned the design of the Accord, repeatedly conducting quantitative impact studies (QIS).

  • According to Basel II, banks should disclose:

    • The entities (banks and other businesses such as securities firms in Europe) to which Basel II rules are applied.

    • A description of the characteristics, terms, and conditions of all the capital instruments held by the bank.

    • A list of the instruments comprising the bank’s Tier 1 capital. The amount of capital provided by each instrument should also be disclosed. 

    • A list of the instruments comprising the bank’s Tier 2 capital.

    • The capital requirements for each type of risk covered under Basel II: credit, market, and operational risks.

    • Information about other bank risks.

    • Information about the bank’s risk management function, how it is structured, and how it operates.

Topic 5. Credit Risk Capital Requirements

  • Basel II specifies three approaches that banks can use to measure credit risk:

    • Standardized approach

    • Foundation internal ratings-based (IRB) approach

    • Advanced IRB approach

Topic 6. CR Capital Requirements: Standardized Approach

  • The standardized approach is used by banks with less sophisticated risk management functions. The risk-weighting approach is similar to Basel I, although some risk weights were changed.

  • Significant changes include:

    • ​OECD status is no longer considered important under Basel II.

    • The credit ratings of countries, banks, and corporations are relevant under Basel II.

    • Bank supervisors may apply lower risk weights when the exposure is to the country in which the bank is incorporated.

    • Bank supervisors may choose to base risk weights on the credit ratings of the countries in which a bank is incorporated rather than on the bank’s credit rating.

    • Risk weights are lower for unrated countries, banks, and companies than for poorly rated countries, banks, and companies.

    • Bank supervisors who elect to use the risk weights under Basel II's standardized approach are allowed to lower the risk weights for claims with maturities less than three months.

    • Additionally, a risk weight of 75% is applied to unrated retail, 35% to unrated mortgage, 0% to cash, and 100% to other.

Topic 6. CR Capital Requirements: Standardized Approach

  • Collateral Adjustments

    • ​Simple Approach: Collateral risk weight replaces counterparty risk weight for covered exposure, with counterparty risk weight applying to uncovered portions and minimum 20% risk weight for collateral

    • Comprehensive Approach: Used by most banks, adjusts exposure size upward and collateral value downward based on volatility of both exposure and collateral value
    • Revaluation Requirement: Collateral must be revalued at minimum every six months under both approaches

Practice Questions: Q1

Q1. Bank Macatawa has a $150 million exposure to Holland Metals Co. The exposure is secured by $125 million of collateral consisting of AA+-rated bonds. Holland Metals Co. is unrated. The collateral risk weight is 20%. Bank Macatawa assumes an adjustment to the exposure of +15% to fallow for possible increases in the exposure and allows for a −25% change in the value of the collateral. Risk-weighted assets for the exposure are closest to:
A. $78.75 million.
B. $93.75 million.
C. $118.13 million.
D. $172.50 million.

Practice Questions: Q1 Answer

Explanation: A is correct.

Exposure = (1.15 × 150) − (0.75 × 125) = 172.5 − 93.75 = $78.75
The risk weight for an unrated corporate counterparty based on Figure 62.5 in the reading is 100%. Applying the 100% risk weight, risk-weighted assets are: risk-weighted assets = 1.0 × 78.75 = $78.75 million.

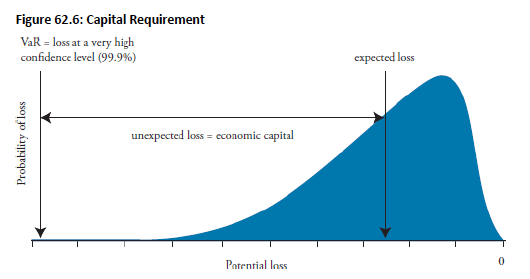
  • U.S. Implementation: Basel II applied only to large U.S. banks, with regulators mandating IRB approach usage rather than offering multiple options
  • IRB Capital Calculation: Capital requirements based on one-year VaR at 99.9% confidence level, following specific regulatory model framework
  • Stress Loss Treatment: Losses exceeding VaR threshold considered stress losses, not covered by allocated economic capital

  • The goal of the IRB approach is to capture unexpected losses (UL). Expected losses (EL) should be covered by the bank’s pricing (e.g., charging higher interest rates on riskier loans to cover EL).

  • The capital required by the bank is thus VaR minus the bank’s EL.

Topic 7. CR Capital Requirements: Internal Ratings-Based (IRB) Approach

  • The VaR can be calculated using a Gaussian copula model of time to default.
    • ​
    •  

  • Here,                is the worst-case probability of default or the default rate at the 99.9 percentile (DR99.9).

  • The bank can be 99.9% certain that the loss from the ith counterparty will not exceed this amount in the coming year.

  • PD is the one-year probability of default of the ith obligor given a large number of obligors, and    is the copula correlation between each pair of obligors.

Topic 7. CR Capital Requirements: Internal Ratings-Based (IRB) Approach

\text{DR99.9} =\mathrm{WCDR}_{\mathrm{i}}=\mathrm{N}\left[\frac{\mathrm{N}^{-1}\left(\mathrm{PD}_{\mathrm{i}}\right)+\sqrt{\rho} \mathrm{N}^{-1}(0.999)}{\sqrt{1-\rho}}\right]
WCDR_i
\rho

  • Assuming the bank has a large portfolio of instruments such as loans and derivatives with the same correlation, the one-year 99.9% VaR is approximately:

    • ​
    •  

  • The capital the bank is required to maintain is the excess of the worst-case loss over the bank’s expected loss defined as follows:

    •  
    •  

  • Note: DR99.9, PD, and LGD are expressed as decimals while EAD is expressed in dollars.

  • DR99.9 increases as the correlation between each pair of obligors increases and as the probability of default increases. If the correlation is 0, then DR99.9 is equal to PD.

  • Basel II assumes a relationship between the PD and the correlation based on empirical research. The formula for correlation is:

    •  

  • Inverse PD-Correlation Relationship: As creditworthiness declines and PD increases, correlation decreases because PD becomes more idiosyncratic and less affected by overall market conditions

Topic 7. CR Capital Requirements: Internal Ratings-Based (IRB) Approach

\operatorname{VaR}_{99.9 \%, 1-\text { year }} \approx \sum_{\mathrm{i}} \mathrm{EAD}_{\mathrm{i}} \times \mathrm{LGD}_{\mathrm{i}} \times \mathrm{DR} 99.9_{\mathrm{i}}
\begin{aligned} \text { Capital } & =\sum_{\mathrm{i}}\left[\mathrm{EAD}_{\mathrm{i}} \times \mathrm{LGD}_{\mathrm{i}} \times \mathrm{DR} 99.9 \mathrm{i}\right]-\sum_{\mathrm{i}}\left[\mathrm{EAD}_{\mathrm{i}} \times \mathrm{LGD}_{\mathrm{i}} \times \mathrm{PD}_{\mathrm{i}}\right] \\ \text { Capital } & =\operatorname{VaR}_{99.9 \%, 1-\text { year }}-\mathrm{EL}\end{aligned}
\rho=0.12 \times\left(1+e^{-50 \times \mathrm{PD}}\right)

  • From a counterparty’s perspective, the capital required for the counterparty incorporates a maturity adjustment as follows:

    • ​
    • where
      •  
      •  
      •  

  • Maturity Adjustment (MA): MA allows for the possibility of declining creditworthiness and/or the possible default of the counterparty for longer term exposures (i.e., longer than one year). If M = 1.0, then MA = 1.0 and the maturity adjustment has no impact.

  • The risk-weighted assets are calculated as 12.5 times capital required:
    •  

  • Capital required equals 8% of RWA, sufficient to cover unexpected losses at 99.9% confidence over one year. Expected losses are covered via pricing.

  • DR99.9 implies a default once every 1,000 years.

  • The Basel Committee may adjust capital via a scaling factor (e.g., 1.06 or 0.98).

Topic 7. CR Capital Requirements: Internal Ratings-Based (IRB) Approach

\begin{aligned} &\mathrm{MA} =\text { maturity adjustment }=[1+(\mathrm{M}-2.5) \times \mathrm{b}] /(1-1.5 \times \mathrm{b}) \\ &\mathrm{M} =\text { maturity of the exposure } \\ &\mathrm{b} =[0.11852-0.05478 \times \ln (\mathrm{PD})]^2 \end{aligned}
\text{RWA }=12.5 \times[\mathrm{EAD} \times \mathrm{LGD} \times(\mathrm{DR} 99.9-\mathrm{PD}) \times \mathrm{MA}]
\text{Capital }=\mathrm{EAD} \times \mathrm{LGD} \times(\mathrm{DR} 99.9-\mathrm{PD}) \times \mathrm{MA}

  • The foundation IRB approach and the advanced IRB approach are similar with the exception of who provides the estimates of LGD, EAD, and M. The key differences are outlined below:

  • Foundation IRB Approach

    • The bank supplies the PD estimate, with a 0.0.3% floor set for bank and corporate exposures

    • The LGD, EAD, and M are supervisory values set by the Basel Committee. The Basel Committee set LGD at 45% for senior claims and 75% for subordinated claims. If there is collateral, the LGD is reduced using the comprehensive approach described earlier.

    • The EAD is calculated similar to the CEA required under Basel I. It includes the impact of netting.

    • M is usually set to 2.5.

  • Advance IRB Approach

    • Banks supply their own estimates of PD, LGD, EAD, and M.

    • PD can be reduced by credit mitigants such as credit triggers subject to a floor of 0.03% for bank and corporate exposures.

    • LGD is primarily influenced by the collateral and the seniority of the debt.

    • With supervisory approval, banks can use their own estimates of credit conversion factors when calculating EAD.​

Topic 8. CR Capital Requirements: Advance IRB Approach

  • The two methods are merged for retail exposures. Banks provide their own estimates of PD, EAD, and LGD.

  • There is no maturity adjustment (MA) for retail exposures.

  • The capital requirement is EAD × LGD × (DR99.9 − PD).

  • Risk-weighted assets are 12.5 × EAD × LGD × (DR99.9 − PD).

  • Correlations are assumed to be much lower for retail exposures than for corporate exposures.

Topic 9. CR Capital Requirements: Foundation and Advance IRB Approaches for Retail Exposures

Topic 10. Operational Risk Capital Requirements

  • Operational Risk Capital: Basel II requires capital for operational risks including internal procedure failures (fraud, improper trading like Barings Bank) and external events (fires), with three calculation approaches: basic indicator, standardized, and advanced measurement
  • Basic Indicator Approach: Simplest method for less sophisticated banks, requiring operational risk capital equal to 15% of three-year average annual gross income (net interest plus non-interest income), excluding negative gross income years from the average
  • Standardized Approach: Similar to basic indicator approach but applies different multipliers to gross income based on specific business lines rather than a single 15% rate
  • Advanced Measurement Approach (AMA): Similar to IRB approach for credit risk, uses one-year VaR at 99.9% confidence level for operational risk losses, allowing banks to incorporate risk mitigating factors like insurance contracts

Practice Questions: Q2

Q2. Which of the following accords first required banks to hold capital for operational risk?
A. Basel I.
B. The 1996 Amendment to Basel I.
C. Basel II.
D. Solvency II.

Practice Questions: Q2 Answer

Explanation: C is correct.

Basel II requires banks to maintain capital for operational risks. Banks can use three methods to measure operational risk. They are the basic indicator approach, the standardized approach, and the advanced measurement approach.

Topic 11. Solvency II Framework

  • In the US and the EU, Solvency II establishes capital requirements for operational, investment, and underwriting risks of insurance companies.

  • Solvency II requires capital buffers above the minimum capital requirement (MCR), called the solvency capital requirement (SCR).

  • SA and IMA are used to determine the SCR under Solvency II.

  • Standardized Approach (SA): Designed for less sophisticated insurance firms unable or unwilling to develop firm-specific risk models, capturing average firm risk profiles and providing cost efficiency for smaller firms with limited risk management capabilities

  • Internal Models Approach (IMA): Similar to Basel II IRB approach, using one-year VaR at 99.5% confidence level with capital charges for underwriting risk (life, non-life, health insurance), investment risk (market and credit), and operational risk

  • QIS and Capital Structure: Regulators use quantitative impact studies (QISs) to assess capital adequacy for significant market events, with insurance companies utilizing three-tier capital structure similar to Basel II (Tier 1: equity/retained earnings, Tier 2: liquidation write-off liabilities, Tier 3: other policyholder-subordinated capital)

  • Internal Model Tests: Insurance companies must satisfy: (1)statistical quality test (data and VaR methodology), (2) calibration test (alignment with industry SCR standards), and (3) use test (model relevance in business decision-making)

Practice Questions: Q3

Q3. Which of the following statements is correct regarding capital requirements for insurance companies?
A. Basel II includes the regulation of banks and insurance companies in the three pillars.
B. The minimum capital requirement is likely to be higher than the solvency capital requirement for insurance companies.
C. The repercussion for violating the solvency capital requirement is likely liquidation and the transfer of company insurance policies to another firm.
D. The internal models approach to calculating the solvency capital requirement is similar to internal rangs-based approach under Basel II in that the firm must calculate a VaR with a oneyear time horizon.

Practice Questions: Q3 Answer

Explanation: D is correct.

Solvency II, not Basel II, establishes capital requirements for insurance companies. The minimum capital requirement (MCR) is just that, a true floor and is thus likely to be lower than the solvency capital requirement (SCR). The repercussion for violating the MCR is likely the prohibition of taking new business and possible liquidation. The repercussion for violating the SCR is the requirement of a plan to remedy the situation and bring the capital back to the required level. The internal models approach is similar to the internal ratings based approach under Basel II in that the insurance company must calculate a one-year VaR with a 99.5% confidence level (versus 99.9% confidence for banks under Basel II).