Watching a quantum system:

How to continuously measure a superconducting qubit

Justin Dressel
Institute for Quantum Studies, Chapman University

 

University of Wisconsin, Madison, October 26th 2017

Current Group

Justin Dressel

 

José Raúl Gonzales Alonso (postdoc)

 

Shiva Lotfallahzadeh Barzili  (grad student)

 

Aaron Grisez (undergrad)

Amy Lam (undergrad)

Michael Seaman (undergrad)

William Parker (undergrad)

Luis Pedro García-Pintos  (postdoc - now at UMB)

Taylor Lee Patti (undergrad - now at Harvard)

Outline

  • Overview of quantum bits (qubits)
    • Superconducting technology update (UC Berkeley)
       
  • Measuring a qubit with microwaves
    • Dispersive coupling
    • Displacement coupling
       
  • Recent results
    • State dragging using the quantum Zeno effect
    • Measuring non-commuting observables concurrently
    • State tomography via classical signal filtering
    • Smoothed past observable estimates and readout

Overview of Quantum Bits

Classical Bit

  • 2 values : 0 or 1
  • Probabilistic state:
     
  • Evolution can only flip:
  • Measurement obeys Bayes' rule:
z = {\small P(1) - P(0) \in [-1,1]},\quad {\small (P(1) + P(0) = 1)}
P(1|r) = \frac{P(r|1)P(1)}{P(r|1)P(1)+P(r|0)P(0)}
1\;{\small (z=1)}
0\;{\small (z=-1)}
z

Quantum Bit (qubit)

  • Continuum of values : Bloch sphere
  • Probabilistic state:
     
  • Evolution precesses: 
  • Measurement obeys Bayes' rule:
\lvert 1\rangle \;{\small (z=1)}
\lvert 0\rangle \;{\small (z=-1)}
\lvert +\rangle \;{\small (x=1)}
\lvert -\rangle \;{\small (x=-1)}
\lvert -i\rangle \;{\small (y=-1)}
\vec{\rho} = {(x,y,z) \in [-1,1]^{\times 3}},\quad {\small (x^2+y^2+z^2 \leq 1)}
\lvert i\rangle
x + iy = e^{-(i\phi+d)/2}\,2\sqrt{P(1)P(0)}
0 \leftrightarrow 1, \; {\small (z \to -z)}
\partial_t \vec{\rho} = \vec{\Omega} \times \vec{\rho}

Overview of Quantum Bits

Quantum Bit (qubit)

  • Continuum of values : Bloch sphere
  • Probabilistic state:
     
  • Evolution precesses: 
  • Measurement obeys Bayes' rule:
\lvert 1\rangle \;{\small (z=1)}
\lvert 0\rangle \;{\small (z=-1)}
\lvert +\rangle \;{\small (x=1)}
\lvert -\rangle \;{\small (x=-1)}
\lvert -i\rangle \;{\small (y=-1)}
\vec{\rho} = {(x,y,z) \in [-1,1]^{\times 3}},\quad {\small (x^2+y^2+z^2 \leq 1)}
\lvert i\rangle
\partial_t \vec{\rho} = \vec{\Omega} \times \vec{\rho}
\hat{\sigma}_z = |1\rangle\!\langle 1| - |0\rangle\!\langle 0|
\hat{\sigma}_x = |1\rangle\!\langle 0| + |0\rangle\!\langle 1|
\hat{\sigma}_y = i|1\rangle\!\langle 0| -i |0\rangle\!\langle 1|
\displaystyle \hat{\rho} = \frac{1}{2}\left[\hat{1} + x\,\hat{\sigma}_x + y\,\hat{\sigma}_y + z\,\hat{\sigma}_z\right]
\hat{1} = |1\rangle\!\langle 1| + |0\rangle\!\langle 0|

Operator Formulation:

State density operator:

\displaystyle \partial_t \hat{\rho} = -i[\hat{\Omega},\,\hat{\rho}] \equiv -i\hat{\Omega}\hat{\rho}+i\hat{\rho}\hat{\Omega}

Evolution precession:

\displaystyle \hat{\Omega} = \frac{1}{2}\left[\omega_x\,\hat{\sigma}_x + \omega_y\,\hat{\sigma}_y + \omega_z\,\hat{\sigma}_z\right]
P(1|r) = \frac{P(r|1)P(1)}{P(r|1)P(1)+P(r|0)P(0)}
\displaystyle \hat{\rho} \to^r\; \frac{\hat{M}_r\hat{\rho}\hat{M}_r^\dagger}{\text{Tr}[\hat{M}_r\rho\hat{M}_r^\dagger]}

Measurement update:

\displaystyle \hat{M}_r = \hat{U}_r\left[\sqrt{P(r|1)}\,|1\rangle\!\langle 1| + \sqrt{P(r|0)}\,|0\rangle\!\langle 0|\right]

Superconducting Qubit: 3D Transmon

\lvert 1\rangle \;{\small (z=1)}
\lvert 0\rangle \;{\small (z=-1)}
\displaystyle \hat{H} = \hbar\hat{\Omega} = \frac{\hbar\omega_q}{2}\hat{\sigma}_z
\hbar\omega_q
\hbar(\omega_q - \delta_q)
\hbar(\omega_q - 2\delta_q)

Qubit energy:

\omega_q/2\pi \sim \text{4--7GHz}
\delta_q/2\pi \sim \text{100--300kHz}

Superconducting Qubit: 3D Transmon

\lvert 1\rangle \;{\small (z=1)}
\lvert 0\rangle \;{\small (z=-1)}
\displaystyle \hat{H}_q = \hbar\hat{\Omega} = \frac{\hbar\omega_q}{2}\hat{\sigma}_z
\hbar\omega_q
\hbar(\omega_q - \delta_q)
\hbar(\omega_q - 2\delta_q)

Qubit energy:

\omega_q/2\pi \sim \text{4--5GHz}
\delta_q/2\pi \sim \text{200MHz}
\displaystyle \hat{H}_r = \hbar\omega_r\hat{a}^\dagger\hat{a}

Cavity mode:

\omega_r/2\pi \sim \text{5--7GHz}
|\Delta|\equiv|\omega_q-\omega_r| \gg g_{\text{q-r}}
\displaystyle \hat{H}_{\text{q-r}} = \hbar g_{\text{q-r}}(\hat{a}+\hat{a}^\dagger)\hat{\sigma}_x
g_{\text{q-r}}/2\pi \sim \text{100MHz}
[\hat{a},\,\hat{a}^\dagger] = \hat{1}

Detuned (dispersive) regime (RWA):

\displaystyle \hat{H}_{\text{q-r}} \sim \hbar \chi\,\hat{a}^\dagger\hat{a}\,\hat{\sigma}_z

X-X Coupling:

\displaystyle \chi \sim \left[\frac{g_{\text{q-r}}}{\Delta}\right]^2\!\delta_q \sim 1\text{MHz}
\displaystyle {\small \chi \neq \frac{g_{\text{q-r}}^2}{|\Delta|}}

Korotkov group, Phys. Rev. A 92, 012325 (2015)

Martinis group, Phys. Rev. Lett. 117, 190503 (2016)

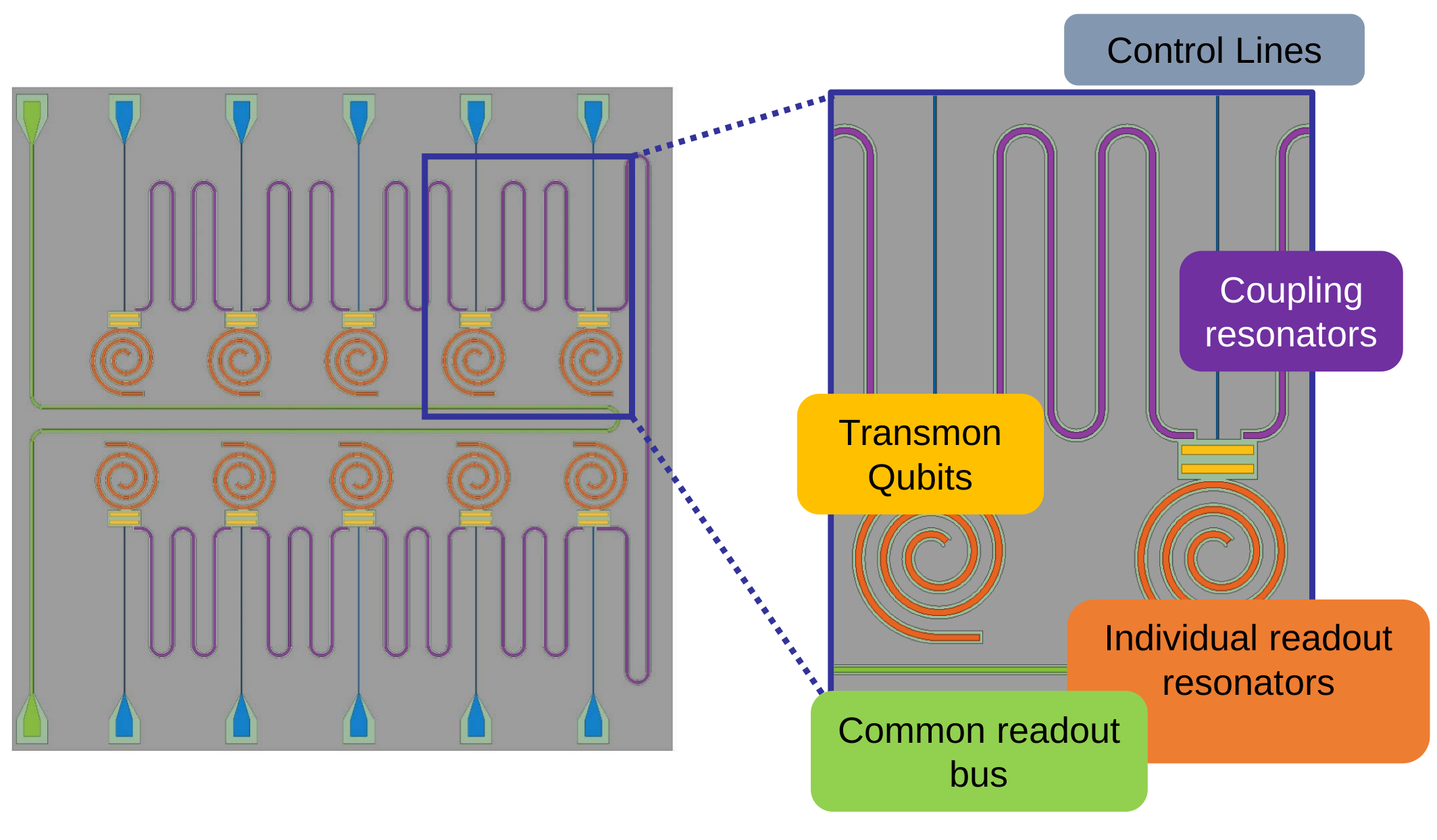
Superconducting Qubit: 2D planar transmon

UCB 10 qubit chip design (v1)

Simultaneous 10 qubit control and readout
Python interface, Jupyter notebook display

v1

v3

Coming soon: two-layer design
separating qubits from control circuitry

Superconducting Qubit: 2D planar transmon

Microwave Measurement : Dispersive Coupling

\hat{H}_{\text{q-r}} = \hbar\chi\,\hat{a}^\dagger\hat{a}\,\hat{\sigma}_z

Dispersive coupling:

Resonator pump:

 

 

Resonator energy decay rate: 

 

Resonant pump produces symmetric photon number:

 

 

 

 

 

Only phase of resonator field is qubit-dependent

Can extract phase with homodyne measurement

\hat{H}_p = \varepsilon^* e^{i\omega_d t}\hat{a} + \varepsilon e^{-i\omega_d t}\hat{a}^\dagger
\partial_t\alpha_\pm = -i(\Delta_{\text{r-d}}\pm\chi)\alpha_\pm - \frac{\kappa}{2}\alpha_\pm -i \varepsilon
\displaystyle \alpha_\pm^{\text{ss}} = \frac{-i\varepsilon}{i(\Delta_{\text{r-d}}\pm\chi) + \frac{\kappa}{2}} \to \frac{-i2\varepsilon/\kappa}{\pm i2\chi/\kappa + 1}
\kappa
\bar{n} = |\alpha^{\text{ss}}_\pm|^2

Markovian Qubit Updates

Discrete Update Model:

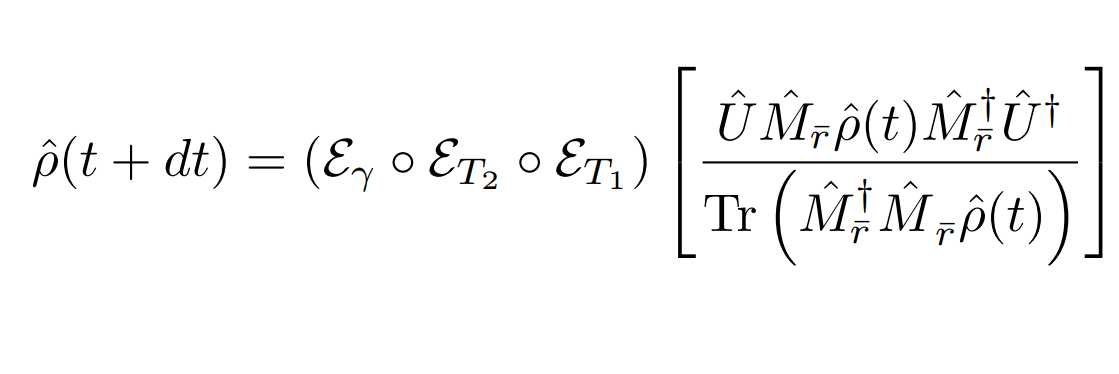
\displaystyle \hat{M}_{\bar{r}} \propto \exp\left[\frac{\bar{r}dt}{2\tau_m}\,\hat{\sigma}_z\,e^{-i\phi}\right]
\hat{U} = \exp(-i\hat{\Omega}t)

(Approximately Gaussian readout with phase-backaction, depends on quadrature phase of amplifier)

T_1 : \text{energy decay time}
T_2 : \text{environmental dephasing}
\eta : \text{measurement quantum efficiency}

(Decomposition assumes dt much smaller than relevant evolution timescales, but longer than the relaxation timescale of resonator)

Koroktov, Phys. Rev. A 94, 042326 (2016)
JD group, Phys. Rev. A 96, 022311 (2017)

\gamma = (1-\eta)/2\tau_m\eta : \text{residual measurement dephasing}

Idea:

  • Measure sequence of independent amplified field segments in outgoing transmission line

 

 

  • The qubit evolves naturally between measurements

    These distinct evolutions compete with each other

 

Assumptions:

  • Each measurement partially collapses the qubit state, assuming the resonator to remain in steady state
  • Uncollected information leaks to environment
  • The qubit energy decays on average

 

Phenomenological nonidealities:

\hat{M}_{\bar{r}} = \hat{U}_{\bar{r}}\left[\sqrt{P(\bar{r}|1)}|1\rangle\!\langle 1| + \sqrt{P(\bar{r}|0)}|0\rangle\!\langle 0|\right]

(Natural qubit evolution and drive)

c_0(t)|0\rangle\otimes|\alpha^{\text{ss}}_-\rangle\otimes|\sqrt{\kappa dt}\,\alpha^{\text{ss}}_-\rangle + c_1(t)|1\rangle\otimes|\alpha^{\text{ss}}_+\rangle\otimes|\sqrt{\kappa dt}\,\alpha^{\text{ss}}_+\rangle
\displaystyle \Gamma_m = \frac{1}{2\tau_m\eta} = \frac{8\chi^2\bar{n}}{\kappa}

Stochastic master equation model:

\Gamma' = 1/T_2 + 1/2\tau_m\eta
\mathcal{D}[\hat{A}]\hat{\rho} = \hat{A}\hat{\rho}\hat{A}^\dagger - (\hat{A}^\dagger\hat{A}\hat{\rho} + \hat{\rho}\hat{A}^\dagger\hat{A})/2
\mathcal{H}[\hat{A}]\hat{\rho} = \hat{A}\hat{\rho}+ \hat{\rho}\hat{A}^\dagger - \text{Tr}(\hat{A}\hat{\rho} + \hat{\rho}\hat{A}^\dagger)\hat{\rho}

(Ito picture - Lindblad dissipation)

(Ito picture - noise innovation)

dW^2 = dt
\bar{r}dt = \langle\hat{\sigma}_z\rangle\,dt + \sqrt{\tau_m}\,dW

(Ito picture - Weiner increment)

(Interpolated stochastic process)

(\text{obtained in limit } dt\to 0 \text{ of discrete model})

Markovian Qubit Updates: Continuous Limit

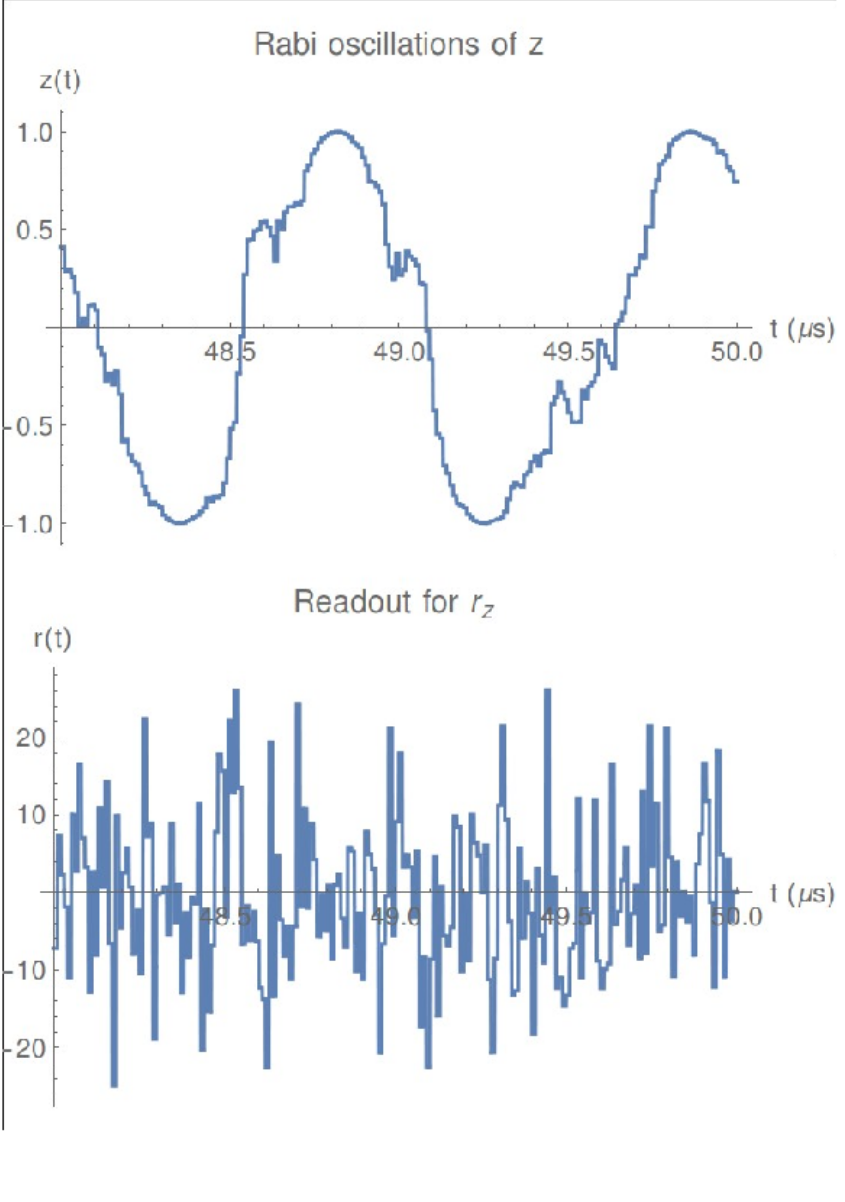
\displaystyle d\hat{\rho} = -i[\hat{\Omega},\hat{\rho}]dt + \frac{\Gamma'}{2} \mathcal{D}[\hat{\sigma}_z]\hat{\rho}dt + \frac{1}{T_1}\mathcal{D}[\hat{\sigma}_-]\hat{\rho}dt
\displaystyle + \sqrt{\frac{1}{4\tau_m}} \mathcal{H}[\hat{\sigma}_z e^{-i\phi}]\hat{\rho}dW

Effective causal readout:

Note: Follows expectation value of Z. We will return to this.

JD group, Phys. Rev. A 94, 062119 (2016)

JD group, Phys. Rev. A 96, 022311 (2017)

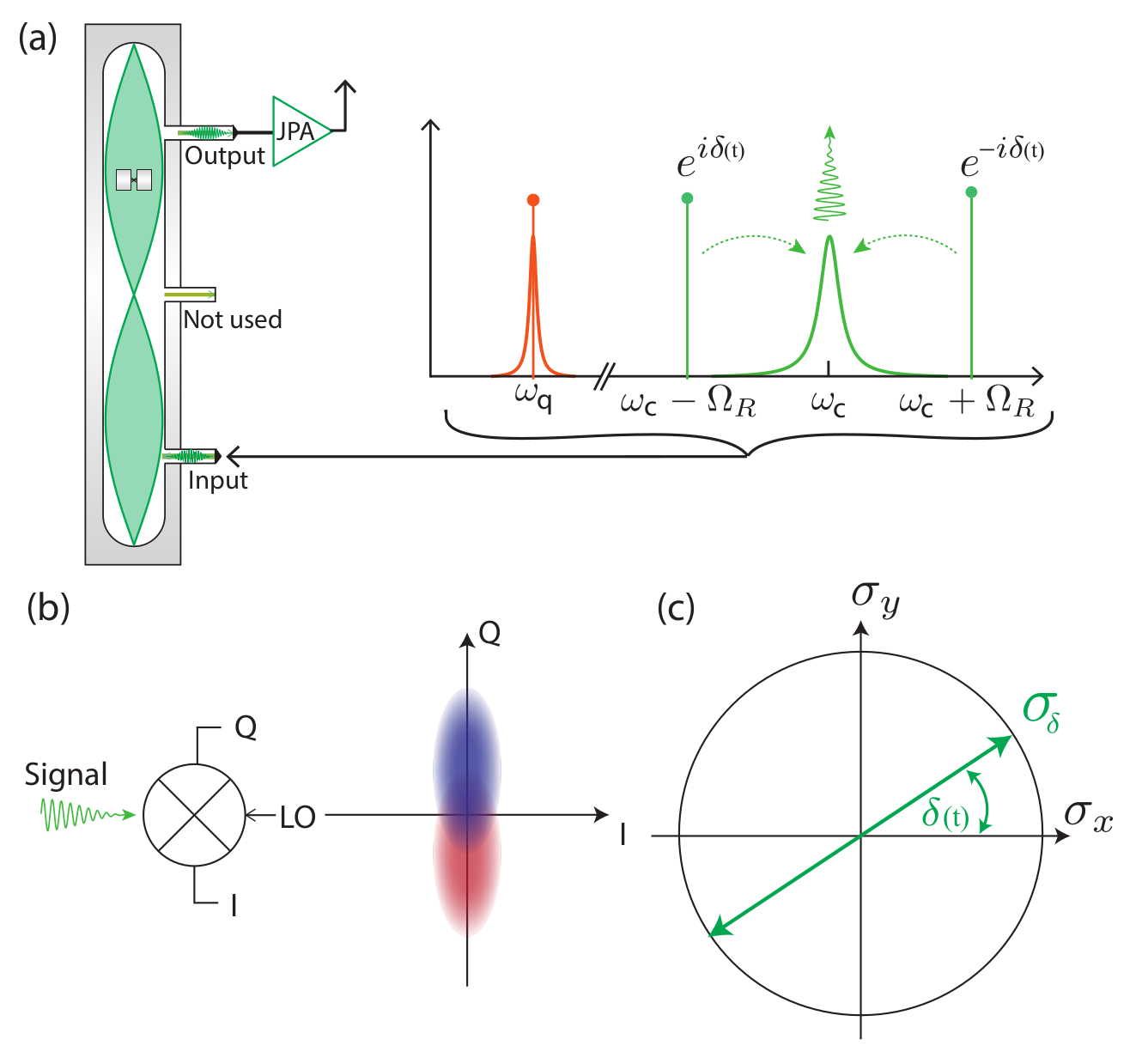
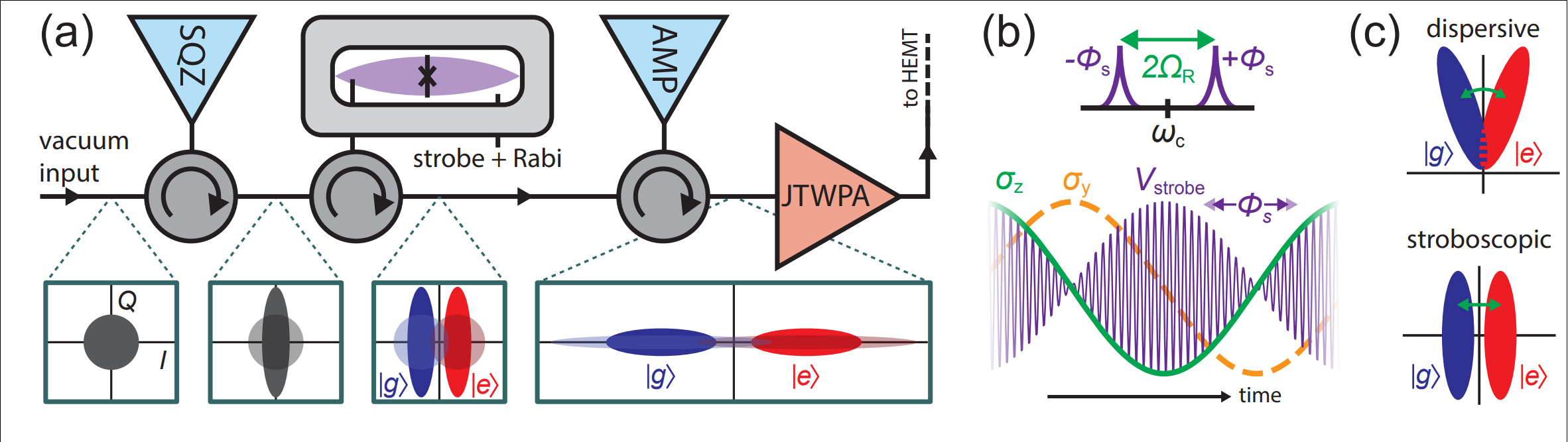
  • Pair of symmetrically detuned pumps
  • Beats stroboscopically measure rotating qubit
  • Yields displacement coupling
     
  • Allows tunable measurement axis
  • Multiple cavity modes = multiple observables 

     
  • Allows squeezed pump field (arXiv:1708.01674)
\hat{H}^{\text{rf}}_{\text{q-r}} = \chi\,(\hat{a}+\hat{a}^\dagger)\,\hat{\sigma}_{\delta}

Displacement coupling:

\hat{\sigma}_{\delta} = \cos\delta\,\hat{\sigma}^{\text{rf}}_x + \sin\delta\,\hat{\sigma}^{\text{rf}}_y

Siddiqi group, Nature 538, 491 (2016)

Microwave Measurement : Displacement Coupling

\hat{H}_{\text{q}} = \frac{\hbar\Omega_R}{2}\hat{\sigma}_x

Rotating frame:

Result: Incoherent Qubit Gate using Quantum Zeno Effect

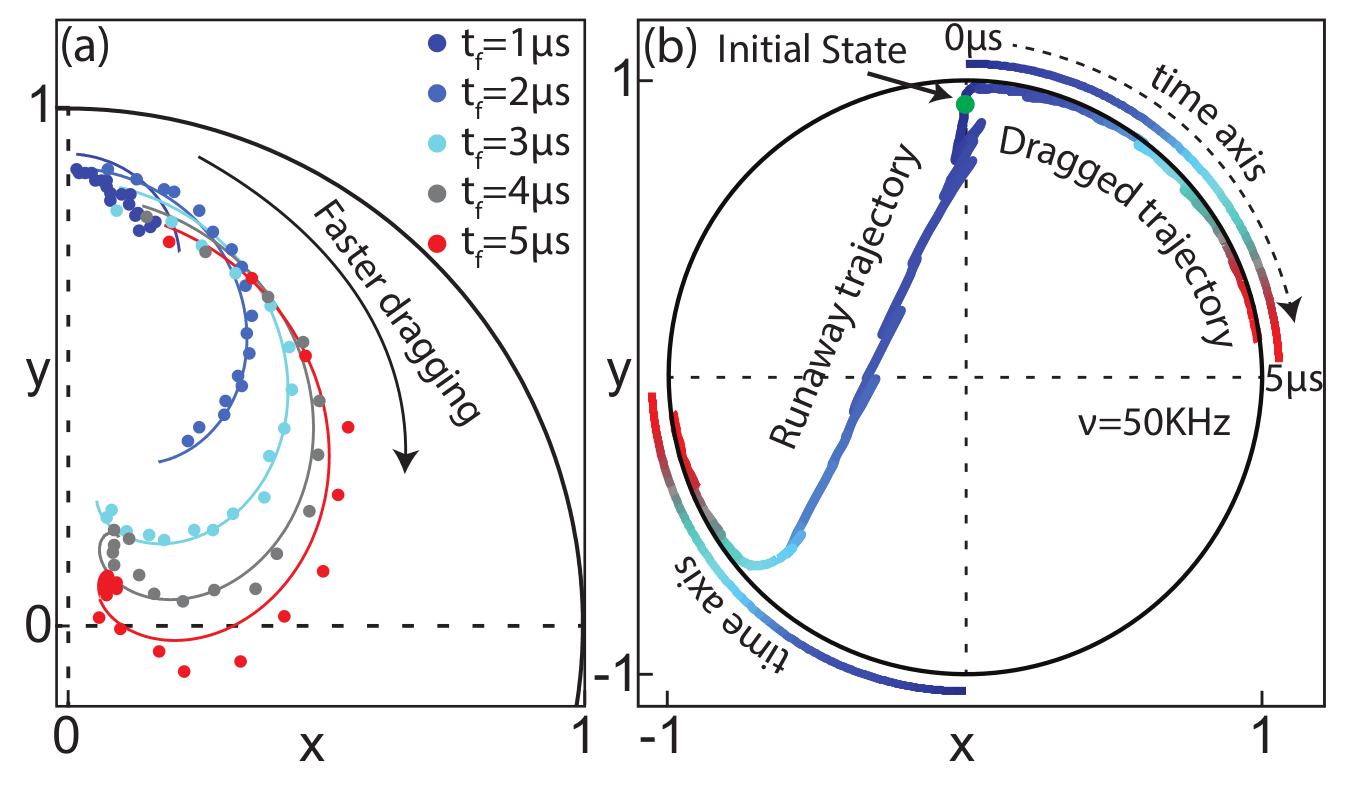
Idea : use time-varying measurement axes to drag the quantum state around the Bloch sphere using the quantum Zeno effect 


The record tracks the state well in this regime, so can be used as a herald for high-fidelity gates

Non-unitary gate

(measurement-based)

\hat{H}_{\text{q-r}}(t) = \chi\,(\hat{a}+\hat{a}^\dagger)\,\hat{\sigma}_{\delta(t)}
\hat{\sigma}_{\delta(t)} = \cos\delta(t)\,\hat{\sigma}_x + \sin\delta(t)\,\hat{\sigma}_y

Stroboscopic displacement coupling can have time-varying side-lobe phases

JD, Siddiqi group, arXiv:1706.08577

Jumps : Faster drag speeds allow trajectories to jump to the opposite pole, decreasing ensemble-averaged dragging fidelity

Jump-axis : Dragging dynamics causes lag of actual Zeno-pinned behind the measurement axis by a fixed angle

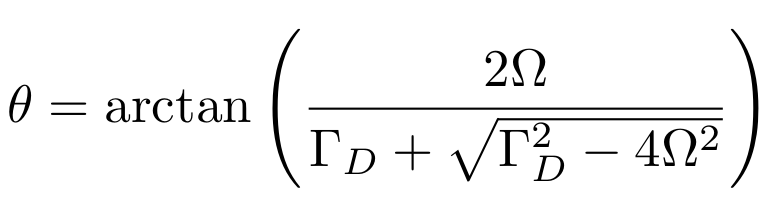
\Omega = 2\pi\,v : \text{dragging frequency}
\Gamma_D = 1/2\tau_m\eta : \text{measurement dephasing rate}

JD, Siddiqi group, arXiv:1706.08577

Pinned to poles : Other than the jumps, state remain pinned to lagged measurement poles

Result: Incoherent Qubit Gate using Quantum Zeno Effect

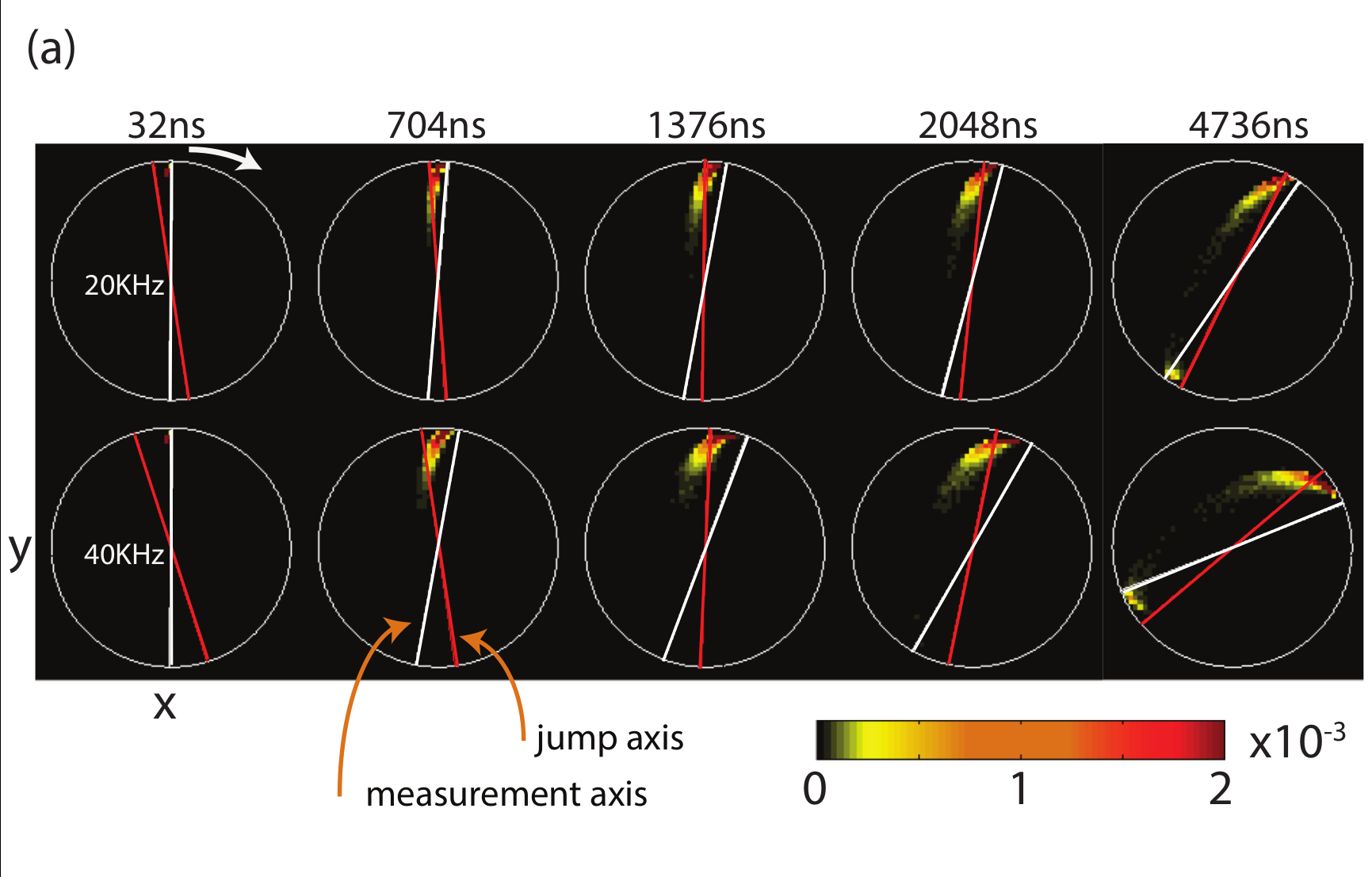
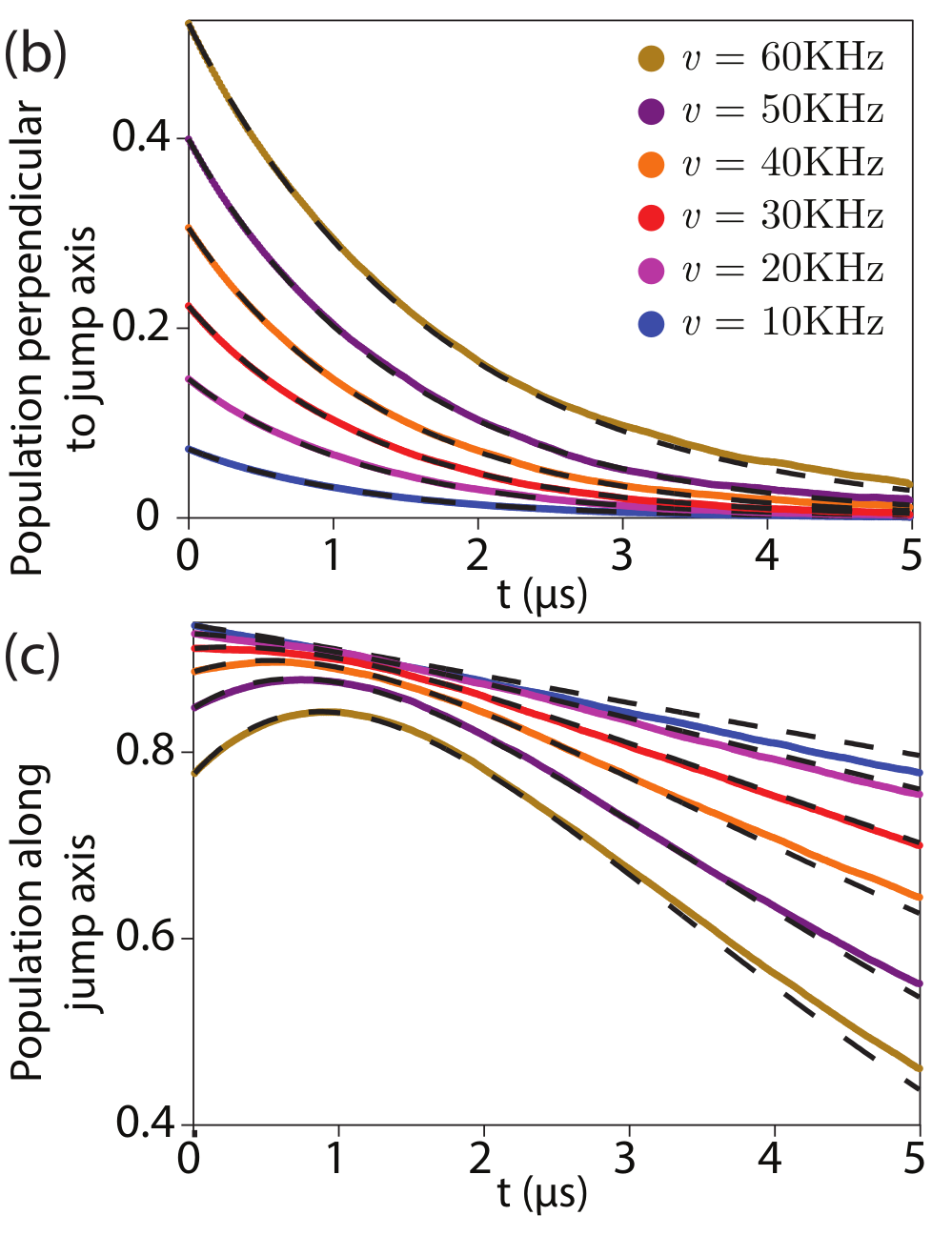
\Omega = 2\pi\,v : \text{dragging frequency}
\Gamma_D = 1/2\tau_m\eta : \text{measurement dephasing rate}

State collapses to jump-axis

JD, Siddiqi group, arXiv:1706.08577

Result: Incoherent Qubit Gate using Quantum Zeno Effect

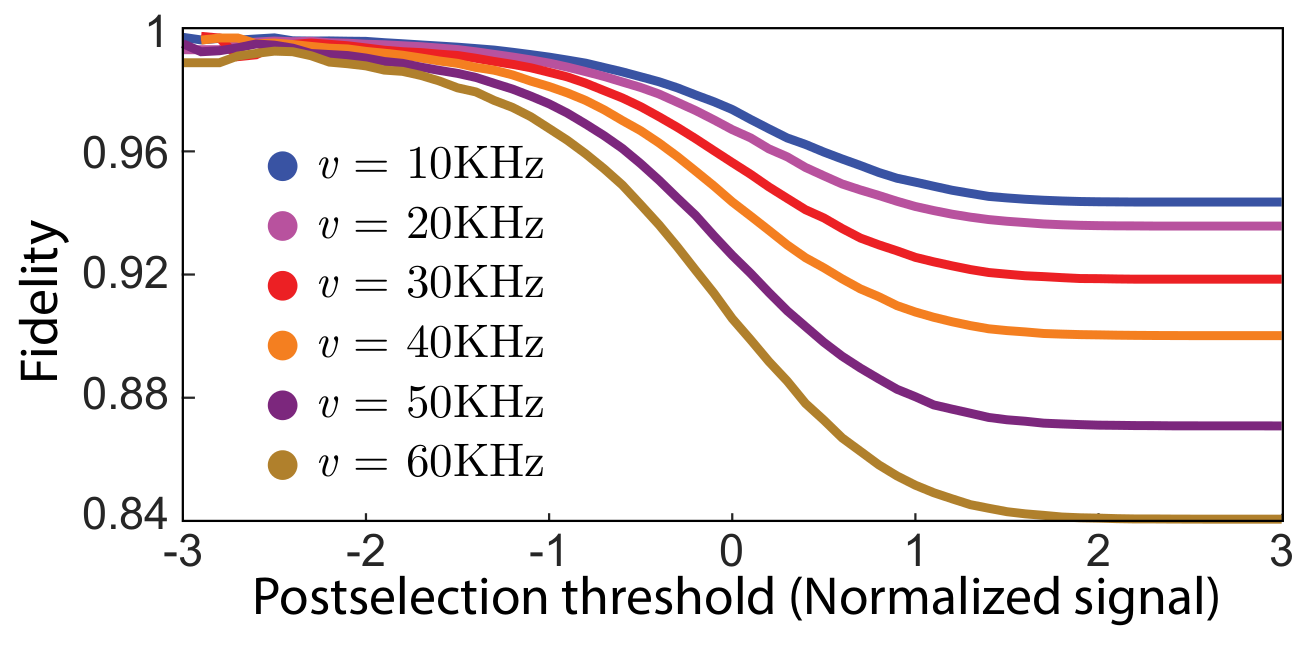
Post-selecting on trajectories with an average readout with a value >1 keeps only trajectories that did not jump, heralding a reasonably high-fidelity dragging gate for that subset

 

Alternatively, the jump may be observed, then corrected later

Result: Incoherent Qubit Gate using Quantum Zeno Effect

Siddiqi group, Nature 538, 491 (2016)

4 pumps, symmetrically detuned from
2 resonator modes of 3D transmon

 

2 simultaneous noncommuting observables

Result : Simultaneous Noncommuting Observable Measurement

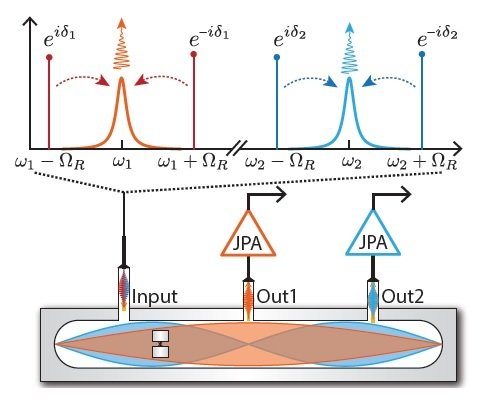
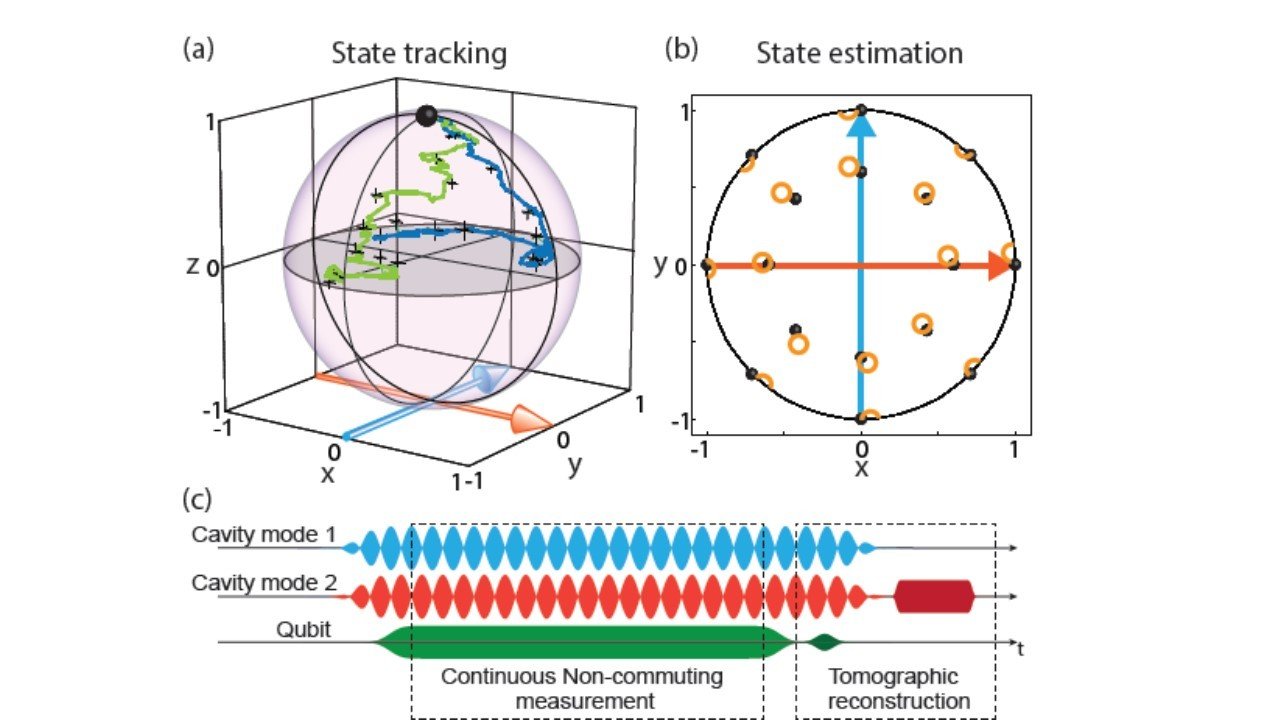
\hat{H}^{\text{rf}}_{\text{q-r}} = \chi_1\,(\hat{a}+\hat{a}^\dagger)\,\hat{\sigma}_{\delta_1} + \chi_2\,(\hat{b}+\hat{b}^\dagger)\,\hat{\sigma}_{\delta_2}
\hat{\sigma}_{\delta_k} = \cos\delta_k\,\hat{\sigma}^{\text{rf}}_x + \sin\delta_k\,\hat{\sigma}^{\text{rf}}_y

Siddiqi group, Nature 538, 491 (2016)

Observable incompatibility leads to diffusion around Bloch sphere

Result : Simultaneous Noncommuting Observable Measurement

Basins of attraction if measurement axes are nearly aligned

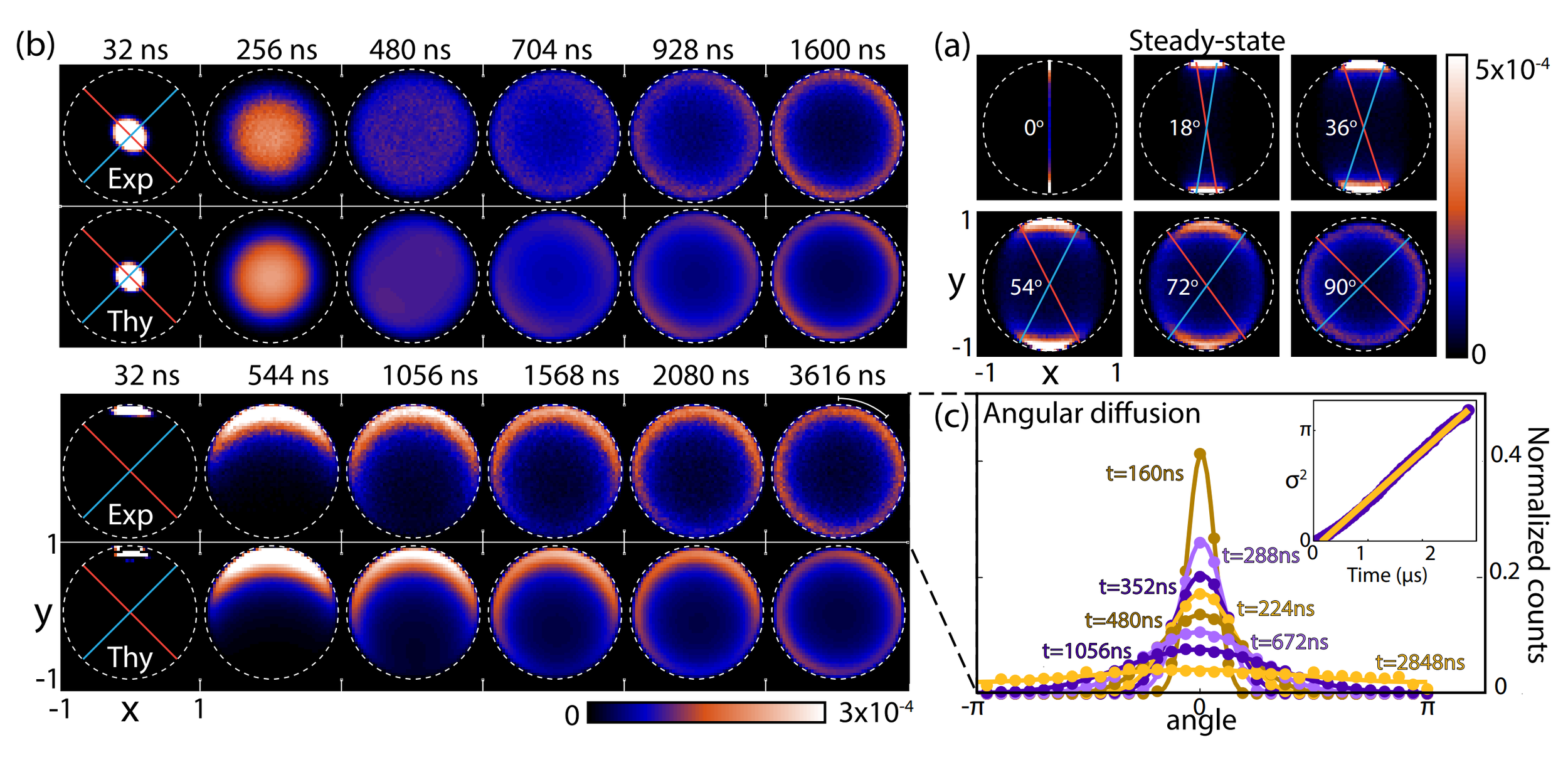
Tracking Quantum Jumps by Filtering Readout

\displaystyle \tau_m \ll 2\pi/\Omega_R

For stronger measurements: noise can be classically filtered to show qubit state

 

Useful for tracking the stochastic jumps between measurement eigenstates

\displaystyle r_k \approx \langle\hat{\sigma}_z\rangle_k + \sqrt{\tau_m}\,\xi_k
\displaystyle H_R = \frac{\Omega_R}{2}\,\hat{\sigma}_x

Rabi drive, qubit oscillations:

Quantum Zeno regime:

Noisy qubit monitoring:

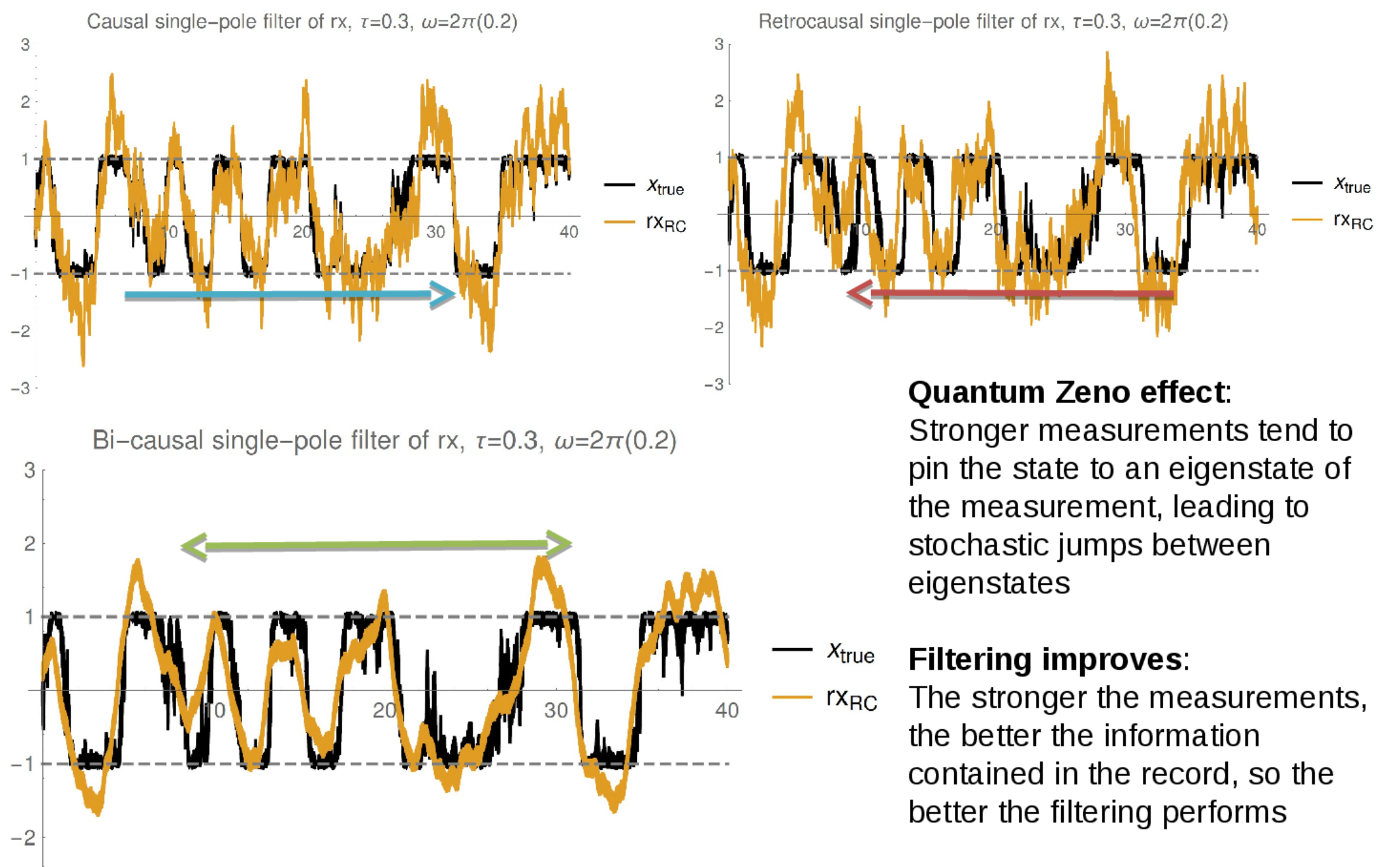
Tracking State with Noncommuting Observable Measurement

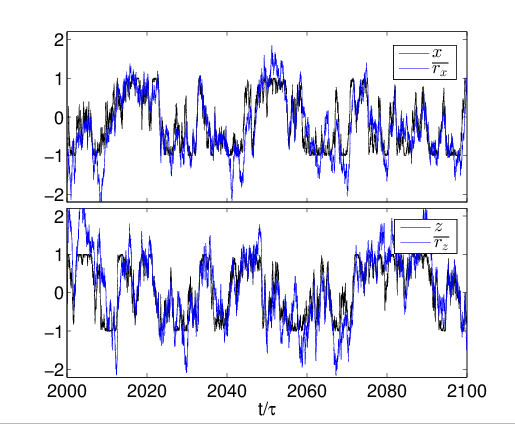
see also Ruskov et al. PRL 105 100506 (2010): >90% state fidelity with 3 axis monitoring + filtering

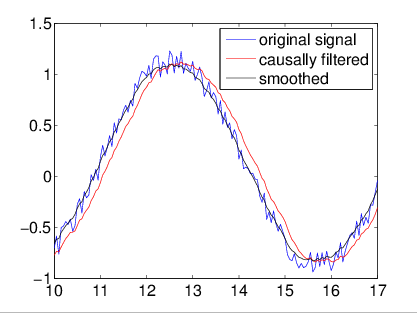
Observation: Since the readouts of each observable (here X and Z) follow the expectation values as they are causally generated, we can track the state using simple classical signal filtering

 

Left: causal exponential filter on readouts (blue) compared to actual simulated expectation values (black), showing reasonable fidelity tracking

 

This works because both measurements can be made sufficiently strong for information to be extracted within the averaging window of the filter

 

Crude state tomography with minimal priors

 

What is the limitation?

JD group, Phys. Rev. A 94, 062119 (2016)

If the collected stochastic signal noisily tracks an observable of the qubit, can we filter the signal to estimate that observable trajectory independently?

Idea: Readout-filtering for tomography

Classical signals can remove Gaussian noise either:
 

1) Causally (no future signal), with a filter (e.g. Weiner, Kalman)
 

2) Non-causally (using future signal), with a smoother

 

For already collected data, smoothers work best

r(t) = z(t) + \sqrt{\tau}\,\xi(t)

Monitored qubit Z operator:

causally generated readout

Signal

Observ. Exp. Value

Gaussian Noise

Structure of collected qubit signal seems amenable to such a filtering technique

 

Filter independent of trajectory model

z(t) = \mathrm{Tr}[Z\,\rho_{\vec{r}_{\mathrm{past}}}]

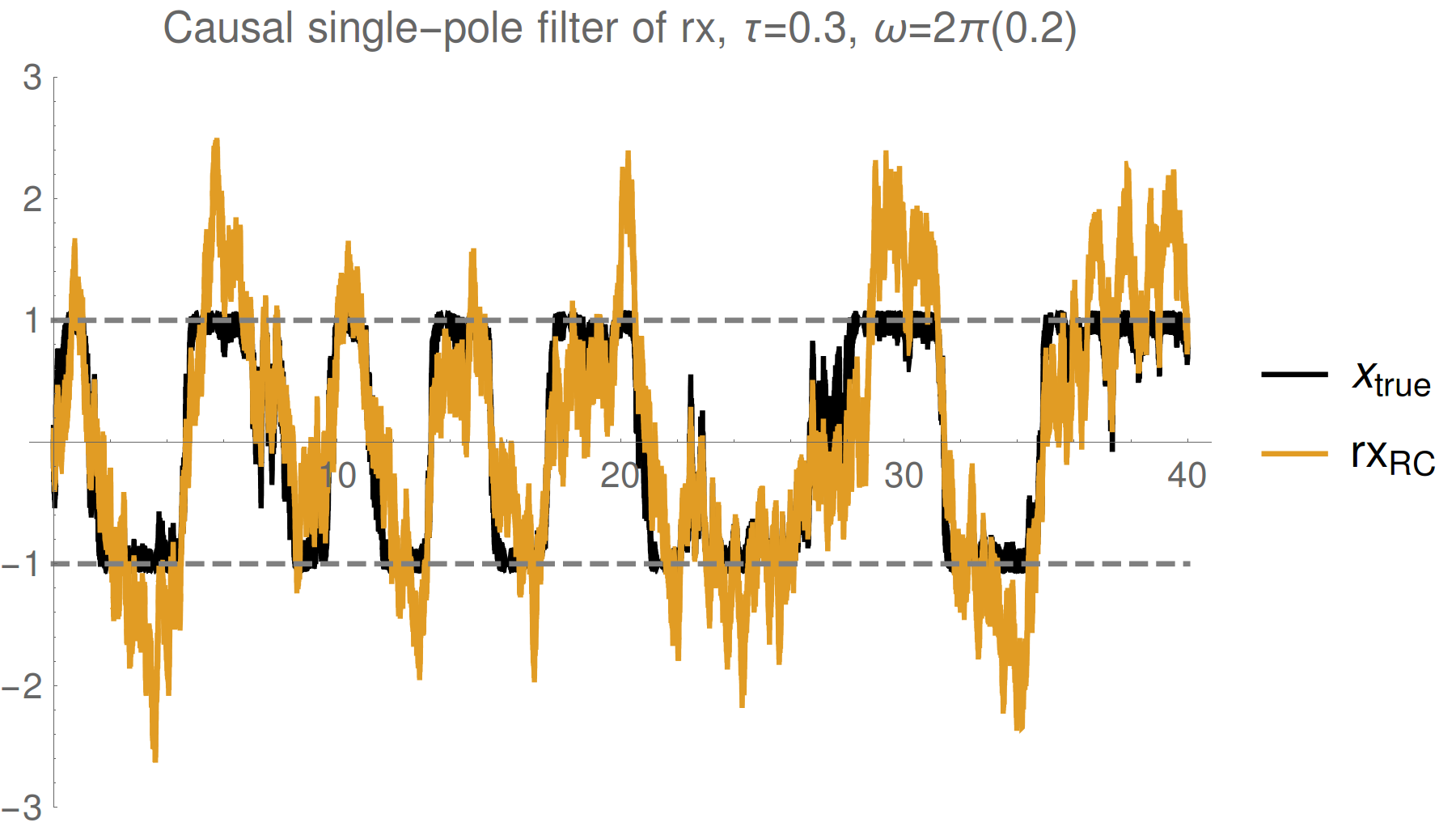
Simple single pole filter

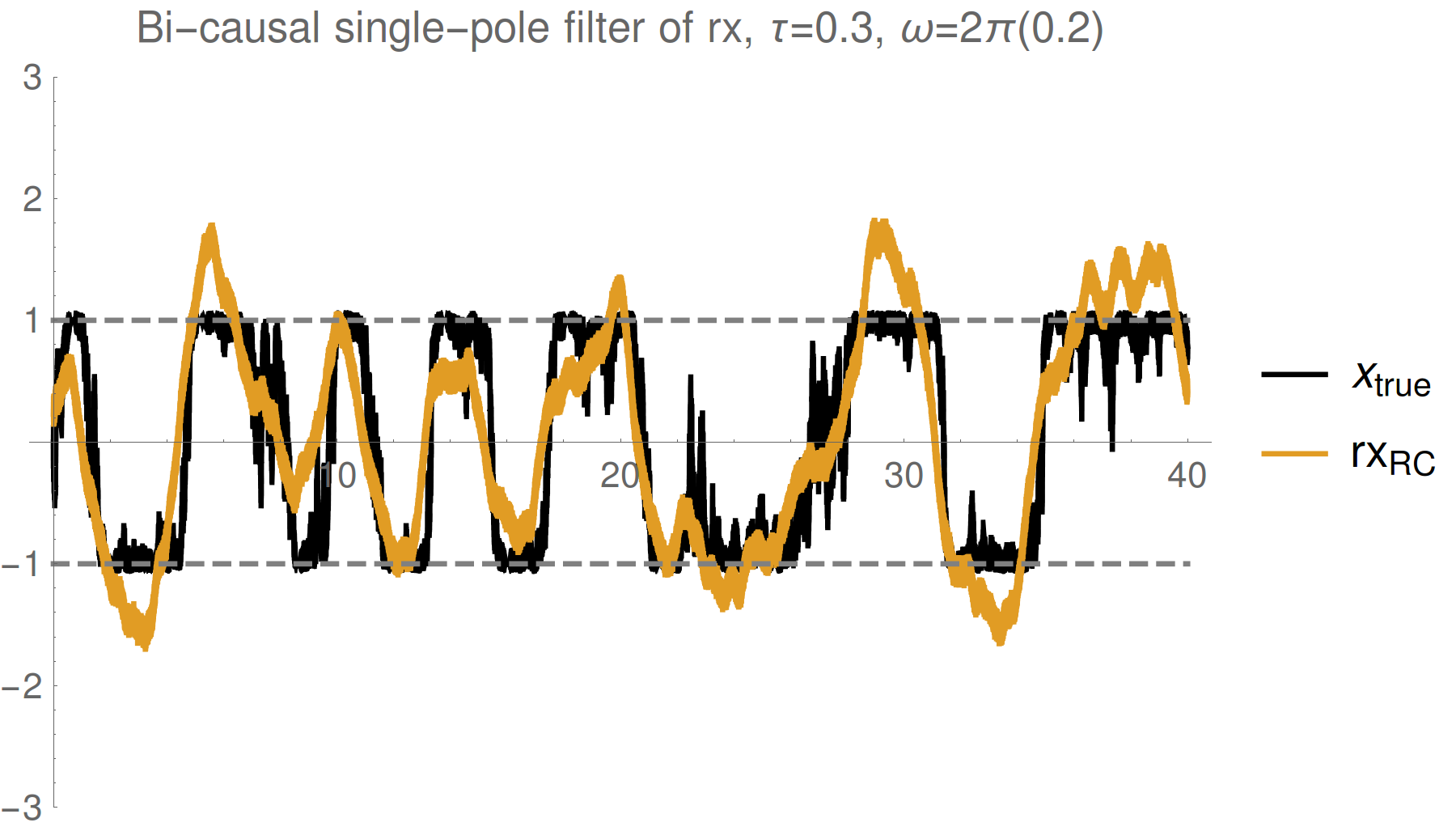
Simple single pole smoother

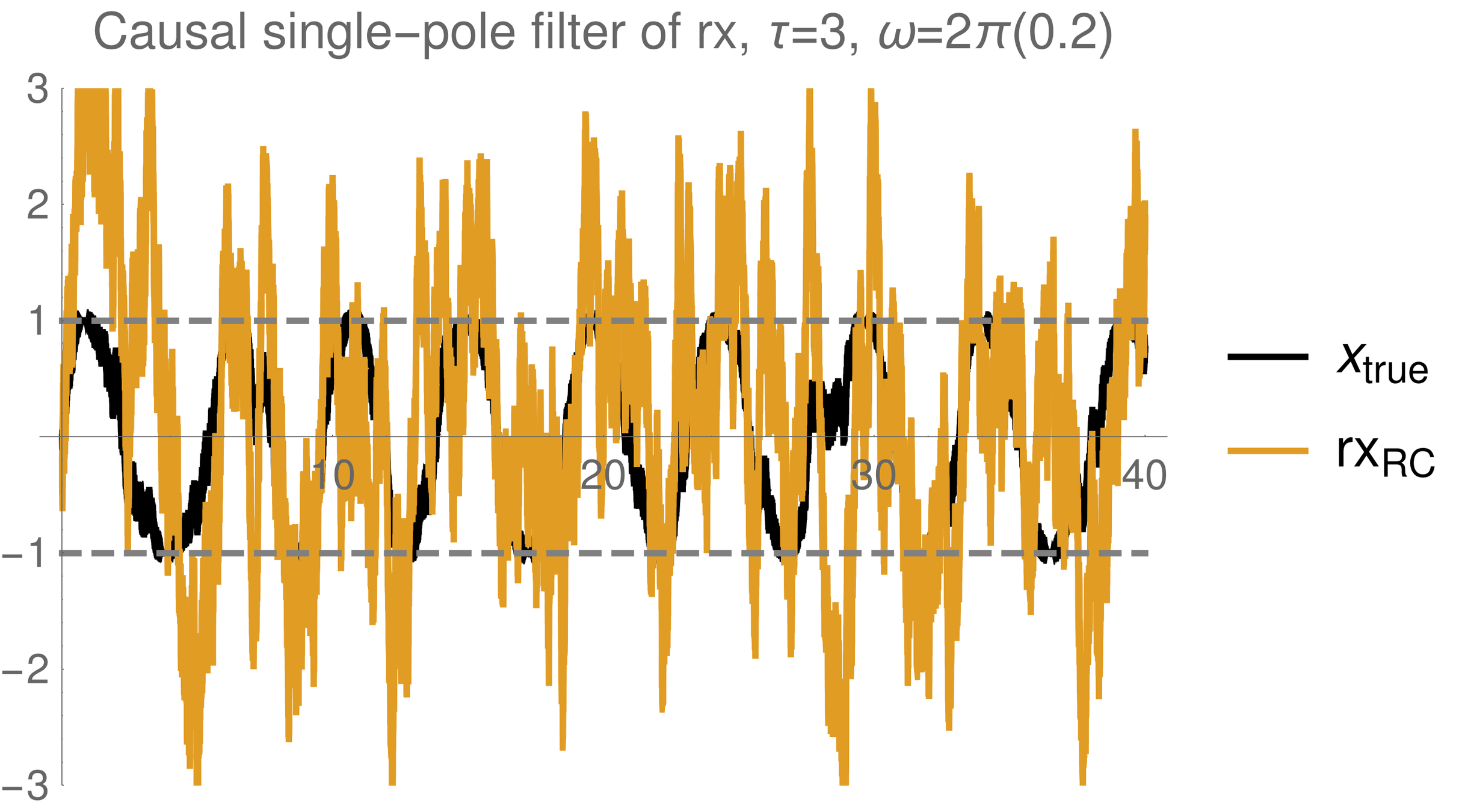
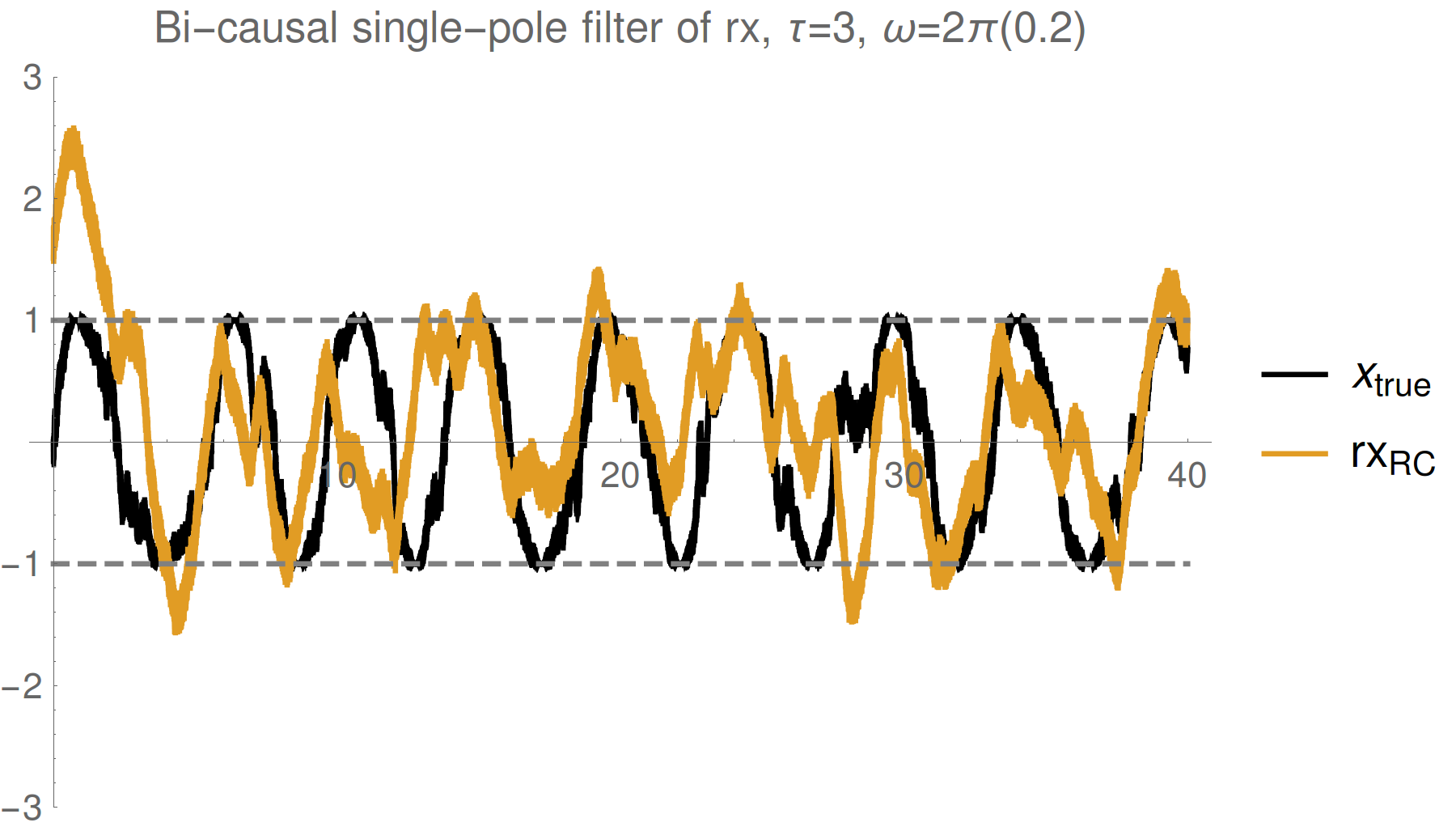
Strong (Zeno) regime: tracking jumps

Weak regime: tracking noisy Rabi oscillations

 Trend : stronger measurements yield more information

--> better fidelity, but more perturbed evolution

Reasonable tracking

Noise harder to remove

Evidence: Readout-filtering for Zeno tracking

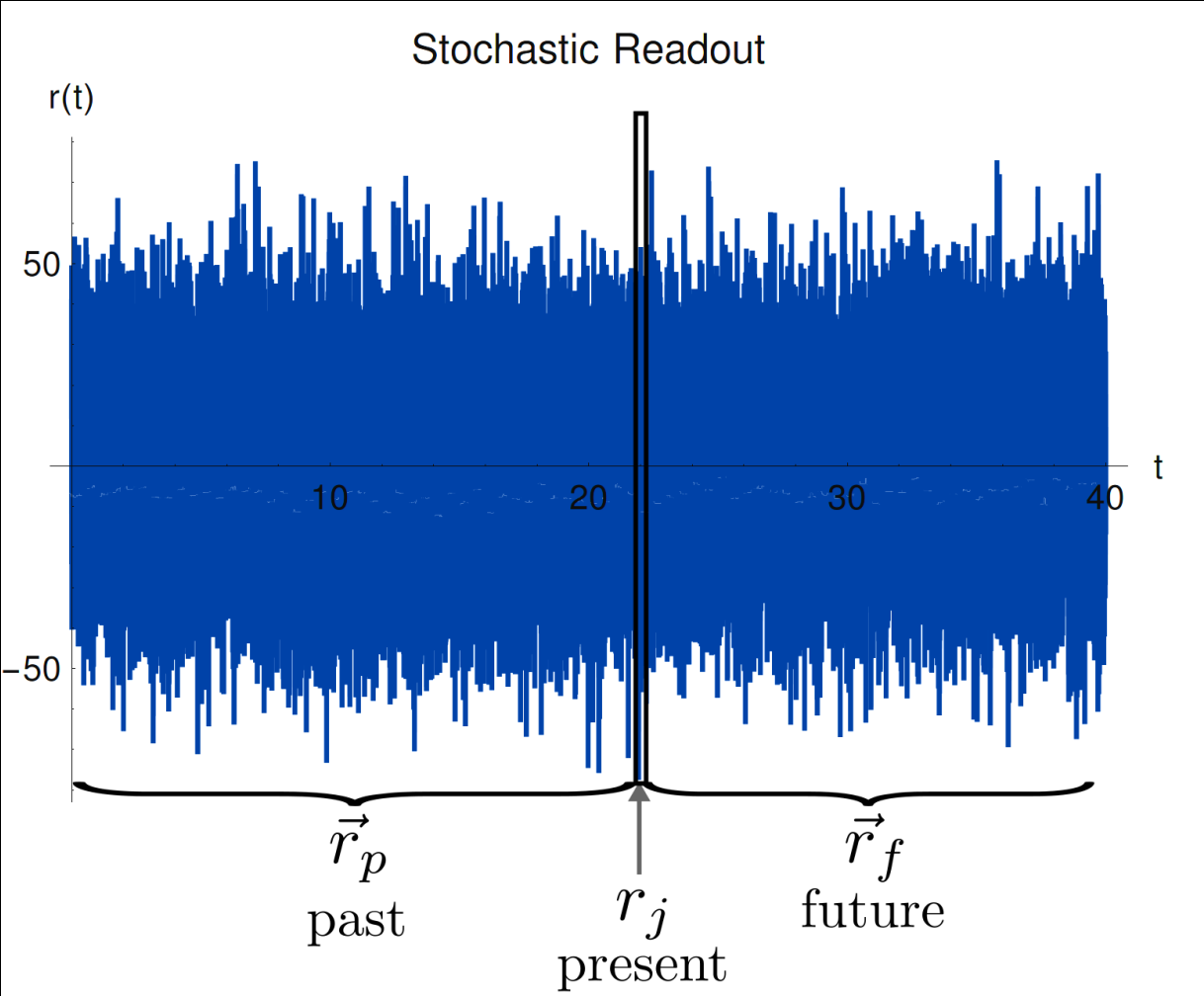
Consider a single collected readout r(t), but omit one point at t=tj.

What distribution P[r(tj)] describes the likelihood of the omitted point?

Result: Shifted Past Readout Distribution

P(r\, |\, \vec{r}_{\mathrm{past}},\, \vec{r}_{\mathrm{future}}) = \frac{P(r,\, \vec{r}_{\mathrm{future}}\,|\,\vec{r}_{\mathrm{past}})}{\sum_r P(r,\, \vec{r}_{\mathrm{future}}\,|\,\vec{r}_{\mathrm{past}})} \approx \frac{\exp\left[-\frac{dt}{2\tau}(r-z_s)^2\right]}{\sqrt{2\pi\tau/dt}}

Discretize time into bins of size dt - assume Markovian Gaussian measurements:

We recover approximate Gaussian noise, as expected:

r(t) = z_s(t) + \sqrt{\tau}\,\xi(t)

However, the collected readout follows a shifted mean value

(Consequence of the measurement backaction producing non-Markovian correlations)

The mean is the expectation value of Z only on the boundary, with unknown future record (as appropriate for simulation)

z
z_s

JD group, arXiv:1708.04362

r(t) = z_s(t) + \sqrt{\tau}\,\xi(t)

Optimally filtering/smoothing a single collected readout

will remove the Gaussian noise, and recover the

shifted observable value, not the expectation value

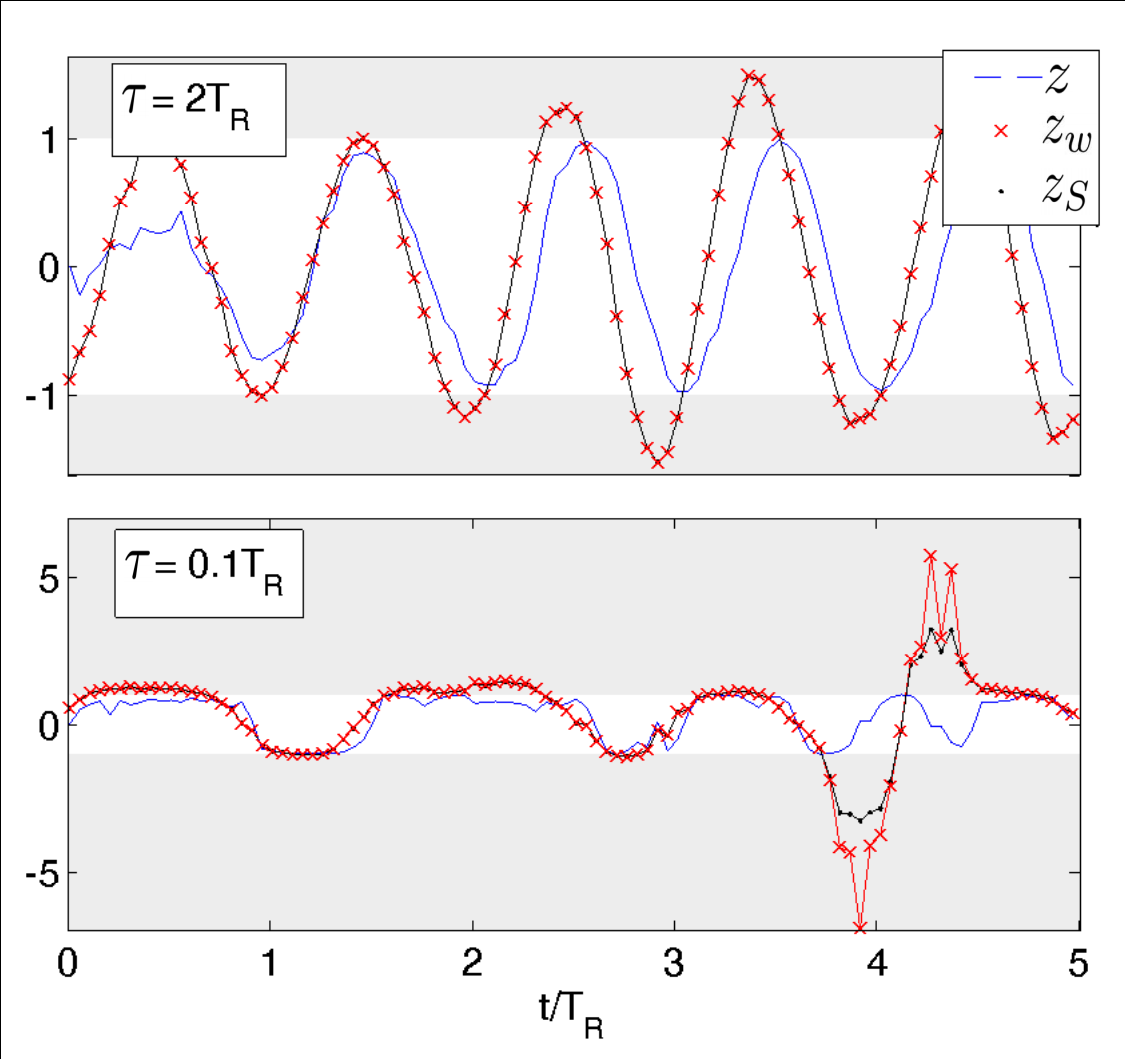
z_s = z_w\, \left[\frac{2}{(1+e^{-dt/2\tau}) + z_c\,(1-e^{-dt/2\tau})}\right] \approx z_w

Weak regime

Strong regime

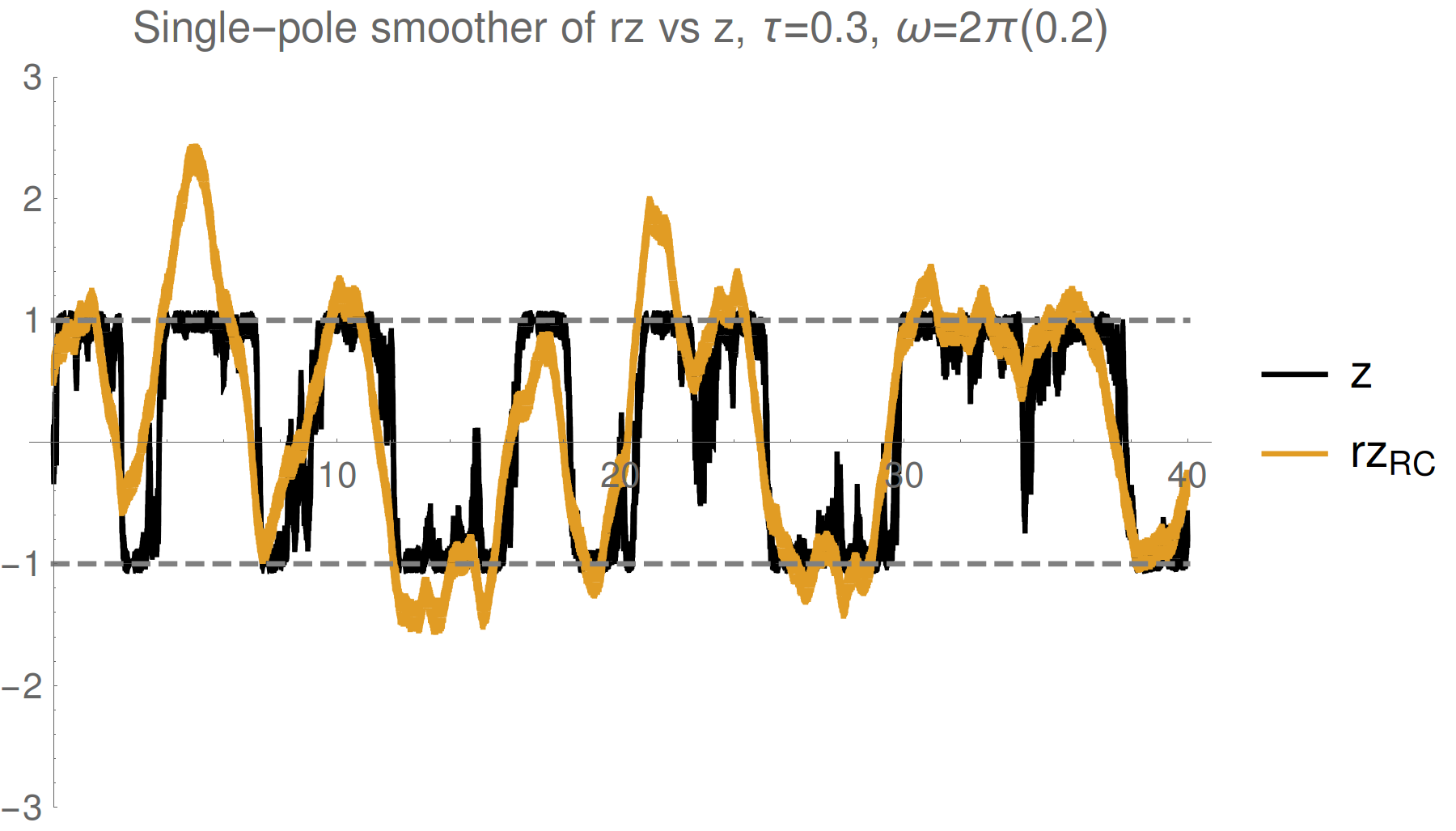
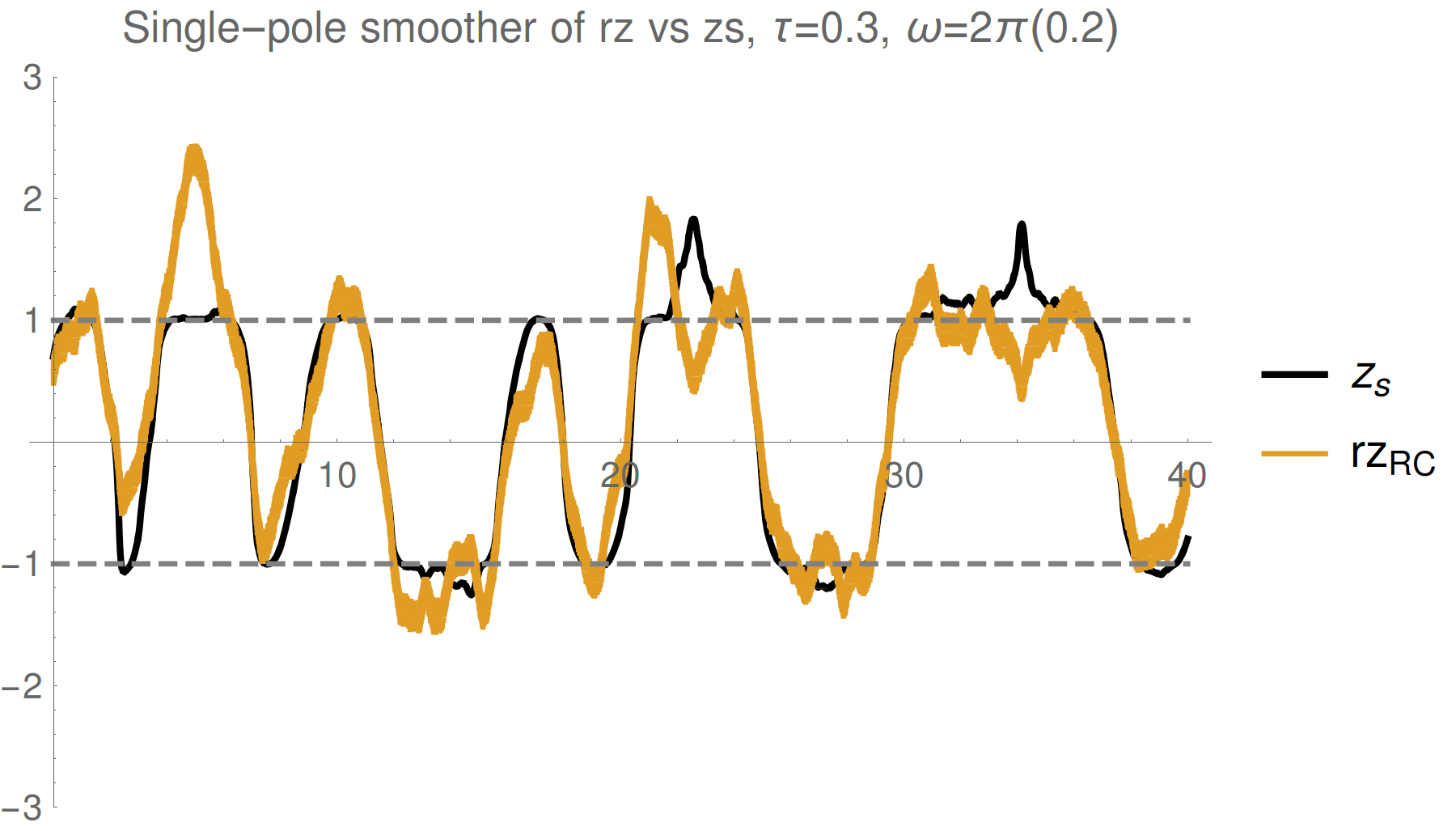
\displaystyle z_w = \mathrm{Re}\frac{\mathrm{Tr}[E_{\vec{r}_{\mathrm{future}}}\,Z\,\rho_{\vec{r}_{\mathrm{past}}}]}{\mathrm{Tr}[E_{\vec{r}_{\mathrm{future}}}\,\rho_{\vec{r}_{\mathrm{past}}}]}

Smoothed (shifted) observable mean:

Depends on a weak value and a quadratric correction:

\displaystyle z_c = \frac{\mathrm{Tr}[E_{\vec{r}_{\mathrm{future}}}\,Z\,\rho_{\vec{r}_{\mathrm{past}}}\,Z]}{\mathrm{Tr}[E_{\vec{r}_{\mathrm{future}}}\,\rho_{\vec{r}_{\mathrm{past}}}]}
\rho_{\vec{r}_{\mathrm{past}}} = \mathcal{M}_{\vec{r}_{\mathrm{past}}}[\rho_0]
E_{\vec{r}_{\mathrm{future}}} = \mathcal{M}^*_{\vec{r}_{\mathrm{future}}}[1]

Non-Markovian dependence on both

past state                          and                 future effect matrix:

Consistent with:

Aharonov PRL 60, 1351 (1988), Wiseman PRA 65, 032111 (2002), Tsang PRL 102, 250403 (2009), Dressel PRL 104, 240401 (2010), Dressel PRA 88, 022107 (2013), Mølmer PRL 111, 160401 (2013)

( No additional ad hoc postselection)

Result: Smoothed Past Observable Estimate

JD group, arXiv:1708.04362

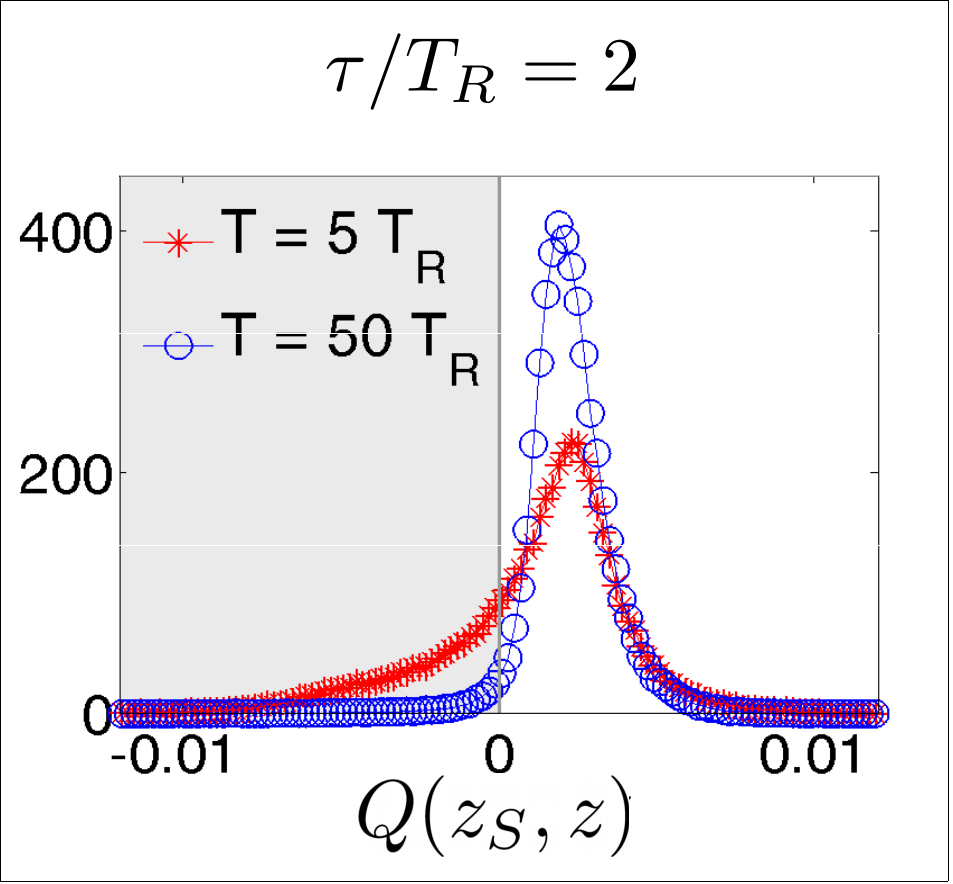
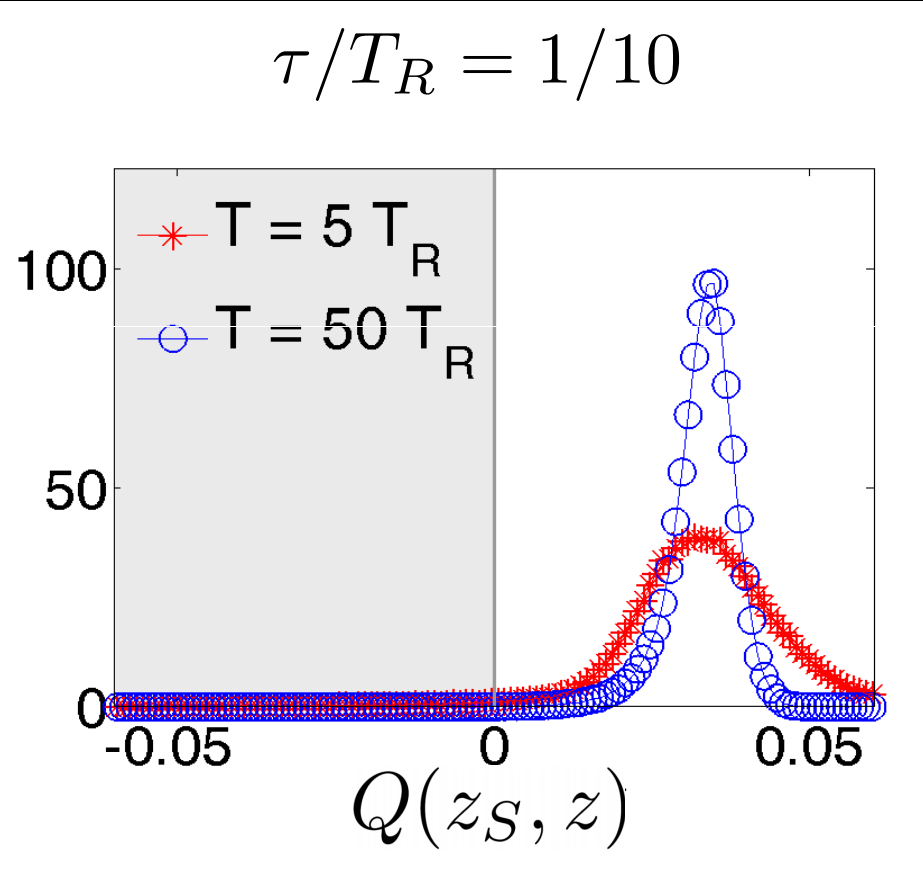
Is this really true? This smoothed value seems strange - can exceed eigenvalue range

Verification 1: look at relative mean-squared error of
both estimates compared to raw readout

Optimal filters/smoothers (Weiner, Kalman, etc.) are often defined to minimize the MSE between a smooth dynamical estimate and the raw noisy signal

\displaystyle Q \equiv \frac{||z - r||^2-||z_S - r||^2}{||z_S - r||^2}

Discriminator:
(>0 implies smoothed value follows readout better than expectation value)

T_R : \mathrm{Rabi\, period}

Strong regime

Weak regime

T : \mathrm{traj.\,length}

smoothed better

Yes. The smoothed value is objectively better by the same metric used for finding classical filters/smoothers.

Result: Smoothed Estimate minimizes MSE

JD group, arXiv:1708.04362

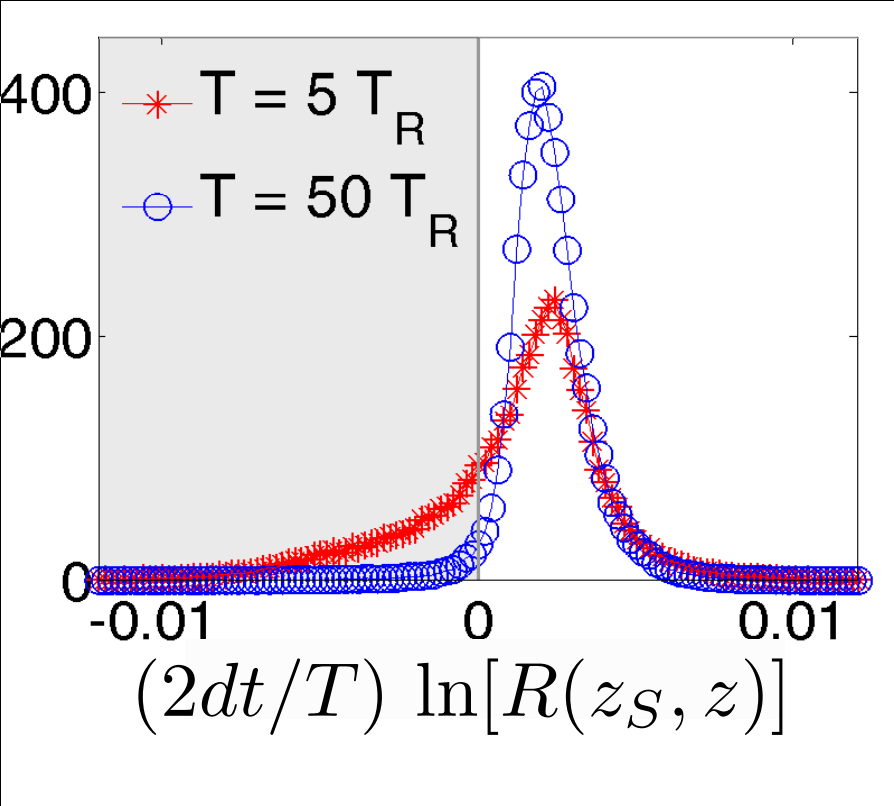
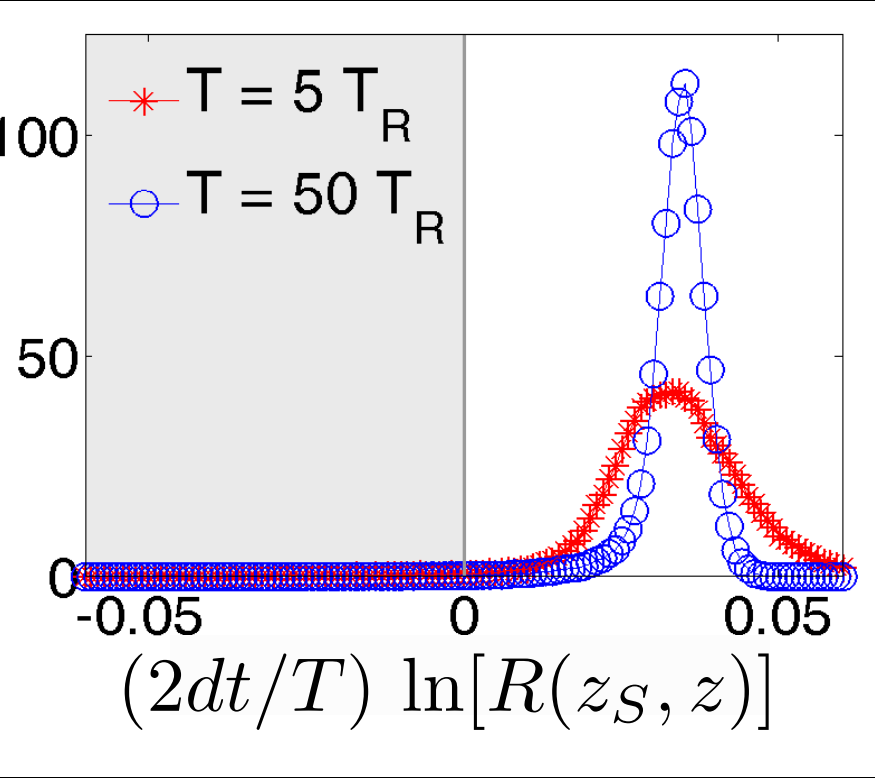
Verification 2: look at relative log-likelihood of
generating the raw readout from adding Gaussian noise to the two estimates - equivalent to a hypothesis test
 

\displaystyle \log(R) \equiv \log\frac{P(r|z)}{P(r|z_s)}

Discriminator:
(>0 implies smoothed value more likely than expectation value to generate readout)

T_R : \mathrm{Rabi\, period}

Strong regime

Weak regime

T : \mathrm{traj.\,length}

smoothed better

Yes. The smoothed value is objectively more likely to generate the observed readout from additive noise

z
z_s

Result: Smoothed Estimate beats Hypothesis Test

JD group, arXiv:1708.04362

Variation: Suppose Bob is weakly monitoring a different observable (X) at the same time

 

If Alice is more strongly monitoring (Z) and has no access to Bob's record, does her smoothed estimate of X (not measured by her) still correspond to Bob's record?

Red : Alice does not know Bob's record, exp. val.

Black : Alice does not know Bob's record, smoothed

Blue : Alice knows both records, smoothed

smoothed better

[Similar question to Guevara, Wiseman PRL 115, 180407 (2015)  ]

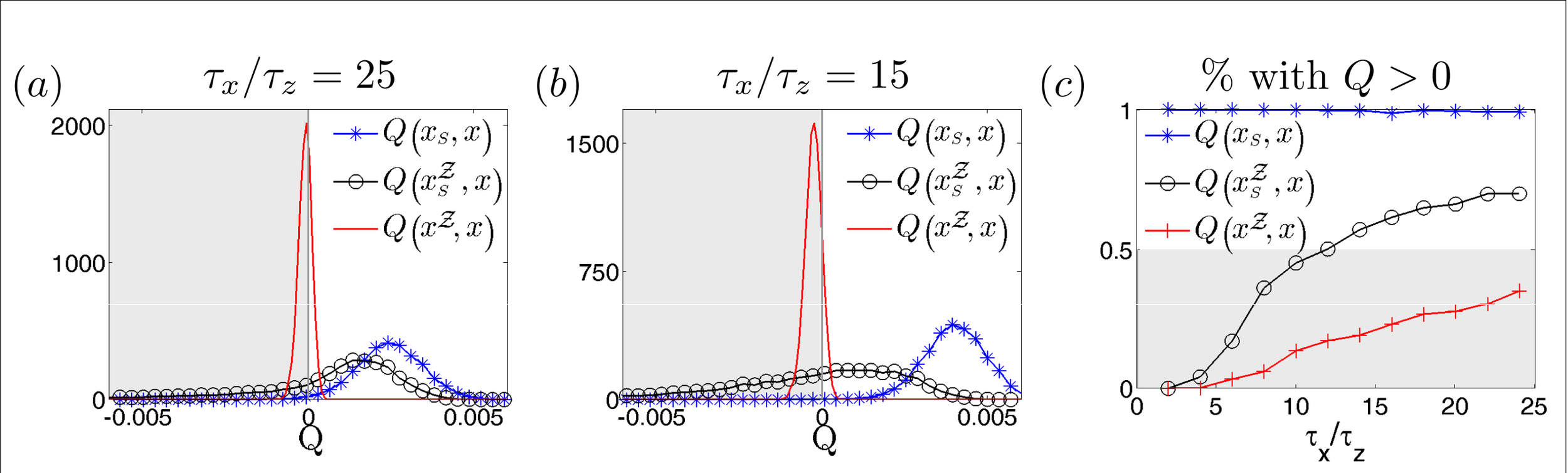
Result: Smoothed Estimate predicts 3rd Party measurement

Yes. Even without access to Bob's record, Alice can construct a smoothed estimate from her record that fits Bob's observed record better than even the expectation value constructed from perfect knowledge of both measurements

 

Smoothed estimate is operationally meaningful

JD group, arXiv:1708.04362

Conclusions

  • Continuous measurements and quantum trajectories can now be used in the laboratory with superconducting transmon circuits
    • 10+ qubit planar 2D transmon designs in-hand at UCB
    • Both dispersive and displacement measurements are possible
       
  • The quantum Zeno effect can be used to produce a heralded measurement-based qubit gate using time-dependent axes
  • Multiple noncommuting observables can be measured simultaneously
  • The stochastic readout collected from a qubit measurement approximates the qubit state for crude tomography, but actually follows a smoothed observable estimate

Thank you!

z_s