When Less is More:

Optical Metrology with
Weak Value Amplification

Justin Dressel

Institute for Quantum Studies

Schmid College of Science and Technology

SACNAS 2019

Outline

  • WVA: Tilt-sensitive Sagnac interferometer
    • Weak value analysis
    • Exact collimated analysis
    • Propagation effects
    • Noise tests
    • Frequency measurement
  • WVA: Phase-sensitive Sagnac interferometer​
    • Displaced Sagnac design
    • Inverse weak value regime response
  • WVA: Remote Sensing Applications
    • Shot noise simulations with low flux
    • Speckle simulations with mode distortion

How can we throw away 99% of our sensing light while keeping 99% of the relevant information?

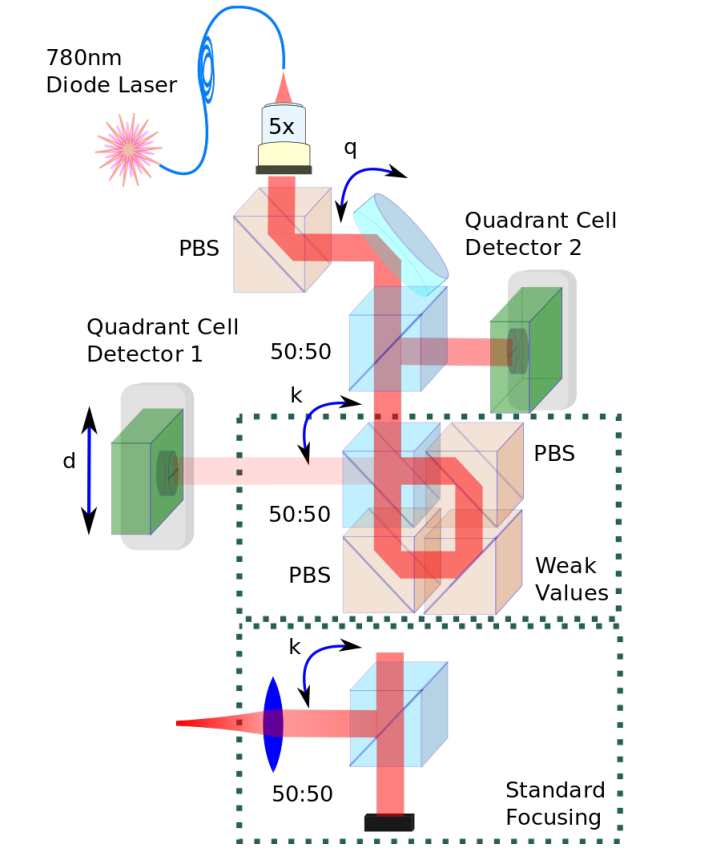
Sagnac Interferometer

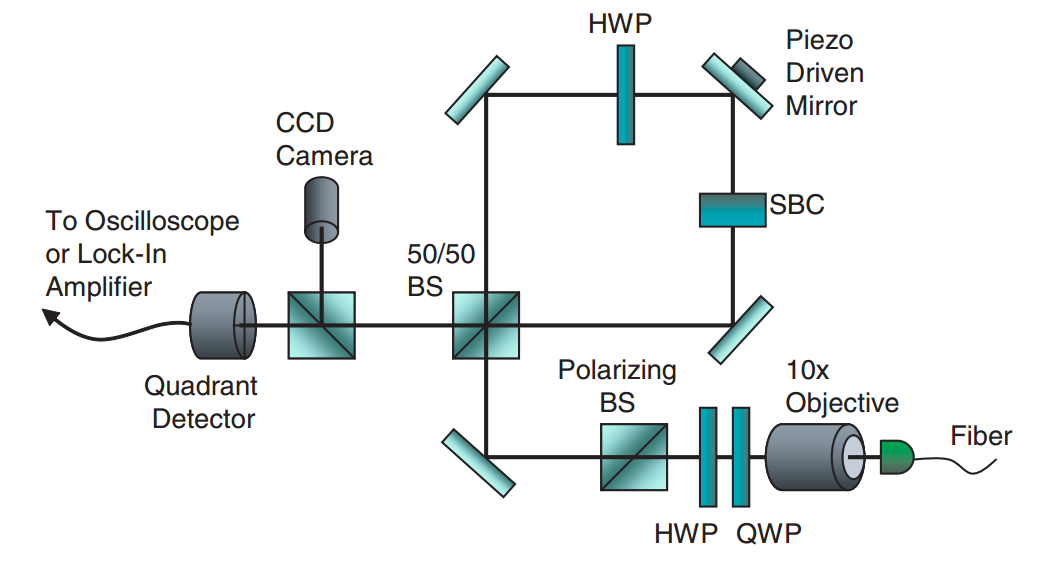
Prototype experiment: Howell lab, Rochester

PRL 102, 173601 (2009)

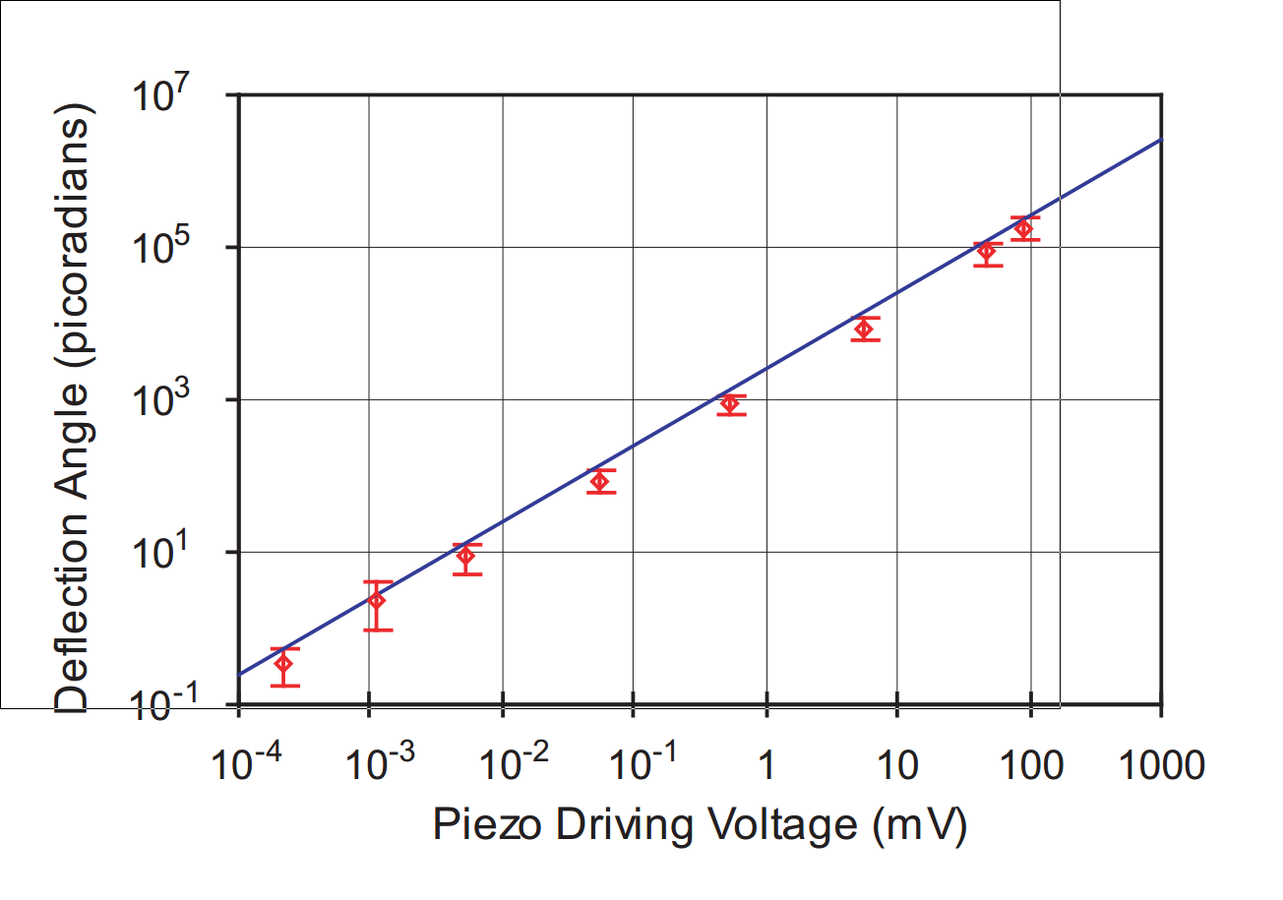
Ultra-sensitive to beam deflection: ~560 femto-radians of tilt detected

\phi\;\text{(phase offset)}
k\;\textbf{(tilt)}
x\;\text{(signal)}
\sigma\;\text{(beam waist)}

General Features of
"Weak Value Amplification" (WVA)

  • Carefully prepared "Preselection State"
    • Input laser profile
    • Initial superposition of paths inside interferometer
  • Intermediate weak interaction that affects branches of superposition slightly differently (to be detected)
    • Small tilt k that breaks symmetry of counter-propagating paths
  • Final "Post-selection" that interferes the branches of the superposition to amplify the interaction effect
    • Collection at "dark port" of interferometer
    • Most light thrown away at "bright port"!

Weak Value Analysis

|i\rangle \propto i|\!\circlearrowleft\rangle + |\!\circlearrowright\rangle
|f\rangle \propto e^{i\phi/2}|\!\circlearrowleft\rangle - ie^{-i\phi/2}|\!\circlearrowright\rangle
|\psi, i\rangle \to \langle p, f | \exp(-i k \hat{x}\hat{W}) | \psi, i \rangle \approx \langle f | i \rangle \langle p - k W_w | \psi \rangle
\hat{W} = |\!\circlearrowleft\rangle\langle\!\circlearrowleft | - |\!\circlearrowright\rangle\langle\!\circlearrowright |
W_w = \frac{\langle f |\hat{W}|i\rangle}{\langle f | i \rangle} = i\cot\frac{\phi}{2} \approx \frac{2i}{\phi}
\phi\;\text{(phase offset)}
k\;\text{(tilt)}
x\;\text{(signal)}
\sigma\;\text{(beam waist)}

Angular tilt (transverse momentum)  amplified by large weak value.

Based on quantum analysis

Weak value regime

k\sigma \ll \phi \ll 1

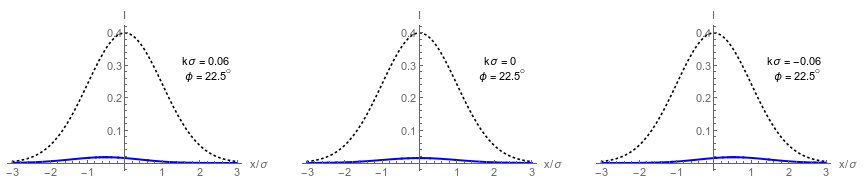
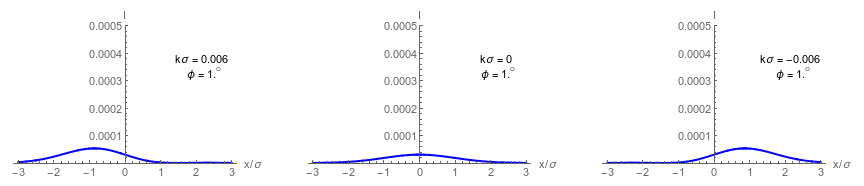
Dark port has single lobe that approximates displaced a Gaussian centered at:

\langle x/\sigma \rangle \propto (\mathbf{k}/\phi)\sigma

Tiny beam deflections can be distinguished, but with low output intensity.

I \propto \phi^2

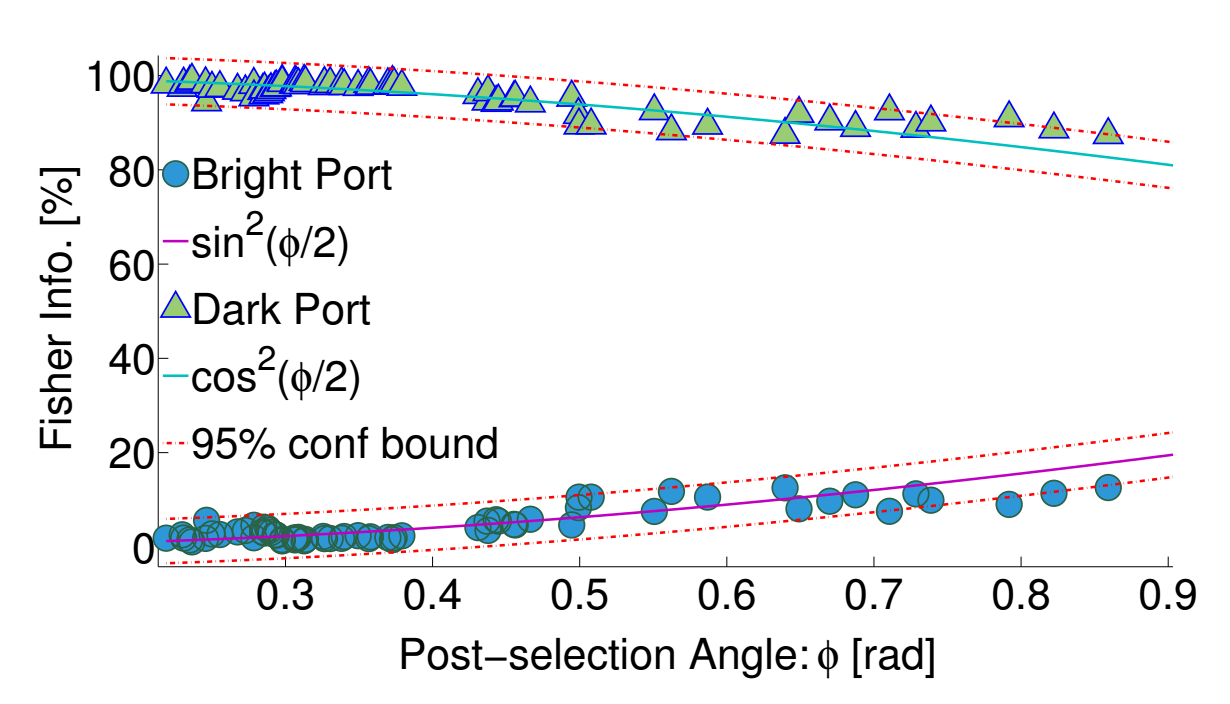
Signal Information vs. Port

  1. Dark port contains almost all information about the signal
  2. Discarded bright port has almost no information
  3. WVA filters the relevant information and suppresses irrelevant noise

Exact Collimated Analysis

|i\rangle = \frac{i|\!\circlearrowleft\rangle + |\!\circlearrowright\rangle}{\sqrt{2}}
|f\rangle = \frac{e^{i\phi/2}|\!\circlearrowleft\rangle - ie^{-i\phi/2}|\!\circlearrowright\rangle}{\sqrt{2}}
|\psi, i\rangle \to \langle x, f | \exp(-i k \hat{x}\hat{W}) | \psi, i \rangle = \langle x|\hat{M}_f\,|\psi\rangle = i\sin(\phi/2 - kx)\langle x | \psi\rangle
\hat{W} = |\!\circlearrowleft\rangle\langle\!\circlearrowleft\! | - |\!\circlearrowright\rangle\langle\!\circlearrowright\! |
\phi\;\text{(phase offset)}
k\;\text{(tilt)}
x\;\text{(signal)}
\sigma\;\text{(beam waist)}
\hat{M}_f = \langle f | \exp(-i k \hat{x}\hat{W}) | i \rangle = i \sin(\phi/2 - k\hat{x})
P(x) = |\langle x,f| \psi,i\rangle|^2 = \sin^2(\phi/2 - kx)\,P_0(x) = \frac{\sin^2(\phi/2 - kx)}{\sqrt{2\pi\sigma^2}} e^{-(x/\sigma)^2/2}

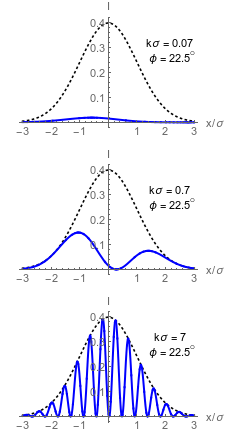
Original profile of beam becomes modulated.

JD et al., PRA  88 , 023801 (2013)

Collimated Dark Port Profiles

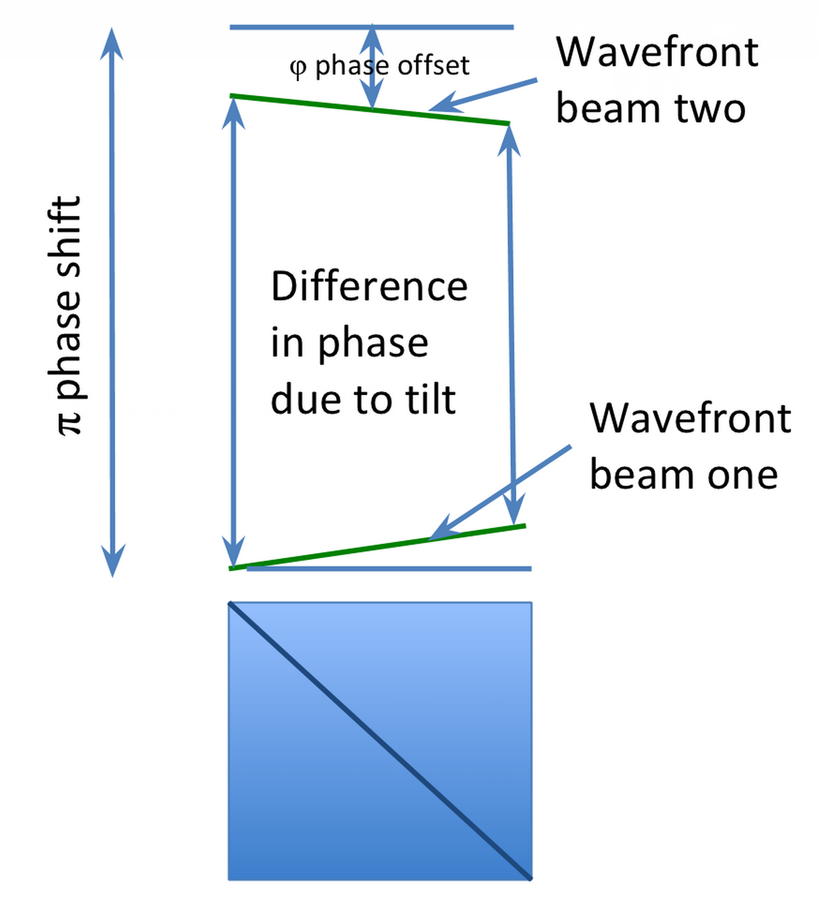
Left: Wavefront tilt mechanism producing spatial modulation

Right: Asymmetric dark port profiles in different regimes

Dashed envelope: input beam intensity

Solid curve:

dark port intensity

 

Top right:

weak value regime
 

 

Middle right:

double lobe regime
 

 

Bottom right:

misaligned regime

k\sigma \ll \phi \ll 1
\phi\ll k\sigma \ll 1
\phi\ll 1 \ll k\sigma

Confirming Noise Performance

WVA vs. Focused spot

Two injected noise sources:

  1. Modulated position jitter at detector (simulated vibration)
  2. Modulated mirror tilt outside interferometer setup

Prototype experiment: Howell lab, Rochester, PRA 92, 032127 (2015)

Goal: compare robustness against technical noise for two theoretically similar (and near optimal) beam deflection techniques

WV Regime with Propagation

|i\rangle = \frac{i|\!\circlearrowleft\rangle + |\!\circlearrowright\rangle}{\sqrt{2}}
|f\rangle = \frac{e^{i\phi/2}|\!\circlearrowleft\rangle - ie^{-i\phi/2}|\!\circlearrowright\rangle}{\sqrt{2}}
|\psi, i\rangle \to \langle x, f | e^{-i\hat{p}^2\ell_2/2k_0}e^{-i k \hat{x}\hat{W}}e^{-i\hat{p}^2\ell_1/2k_0}e^{iq\hat{x}} | \psi, i \rangle = \langle x|\hat{M}_f\,|\psi\rangle
\hat{W} = |\!\circlearrowleft\rangle\langle\!\circlearrowleft\! | - |\!\circlearrowright\rangle\langle\!\circlearrowright\! |
\phi\;\text{(phase offset)}
k\;\text{(tilt)}
x\;\text{(signal)}
\sigma\;\text{(beam waist)}
\hat{M}_f = i e^{-i\hat{p}^2\ell_2/2k_0}\sin(\phi/2 - k\hat{x})e^{-i\hat{p}^2\ell_1/2k_0}e^{iq\hat{x}}
\int xP(x|f)dx = \frac{\int x|\langle x,f| \psi,i\rangle|^2dx}{\int|\langle x,f| \psi,i\rangle|^2dx} \approx \displaystyle \mathbf{\frac{k}{\phi}}\left[4\sigma^2 + \frac{\ell_1(\ell_1+\ell_2)}{k_0^2\sigma^2}\right] + \frac{\mathbf{q}(\ell_1+\ell_2)}{k_0} + \cdots

Tilted input q not amplified, but tilt k inside device is amplified.

ANJ et al., PRX  4 , 011031 (2014)

q\;\text{(tilted input)}
\ell_1,\ell_2\;\text{(propagation lengths)}

Injected Noise Robustness

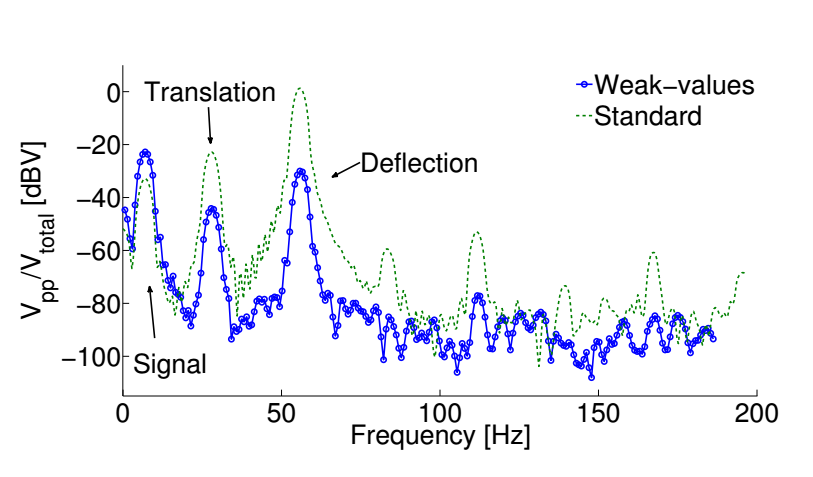
  1. Modulation of signal mirror enhanced by 10dBV
  2. Modulation noise of detector position suppressed by 20dBV
  3. Modulation noise of external tilt suppressed by 30dBV
  4. Non-injected noise floor generally suppressed

Passive Laser Noise Results

  1. No modulated signal added - passive random background
  2. No spatial mode filtering of raw laser output:
    random mode fluctuations below 300 Hz expected.
  3. WVA suppresses passive laser noise by 20dBV

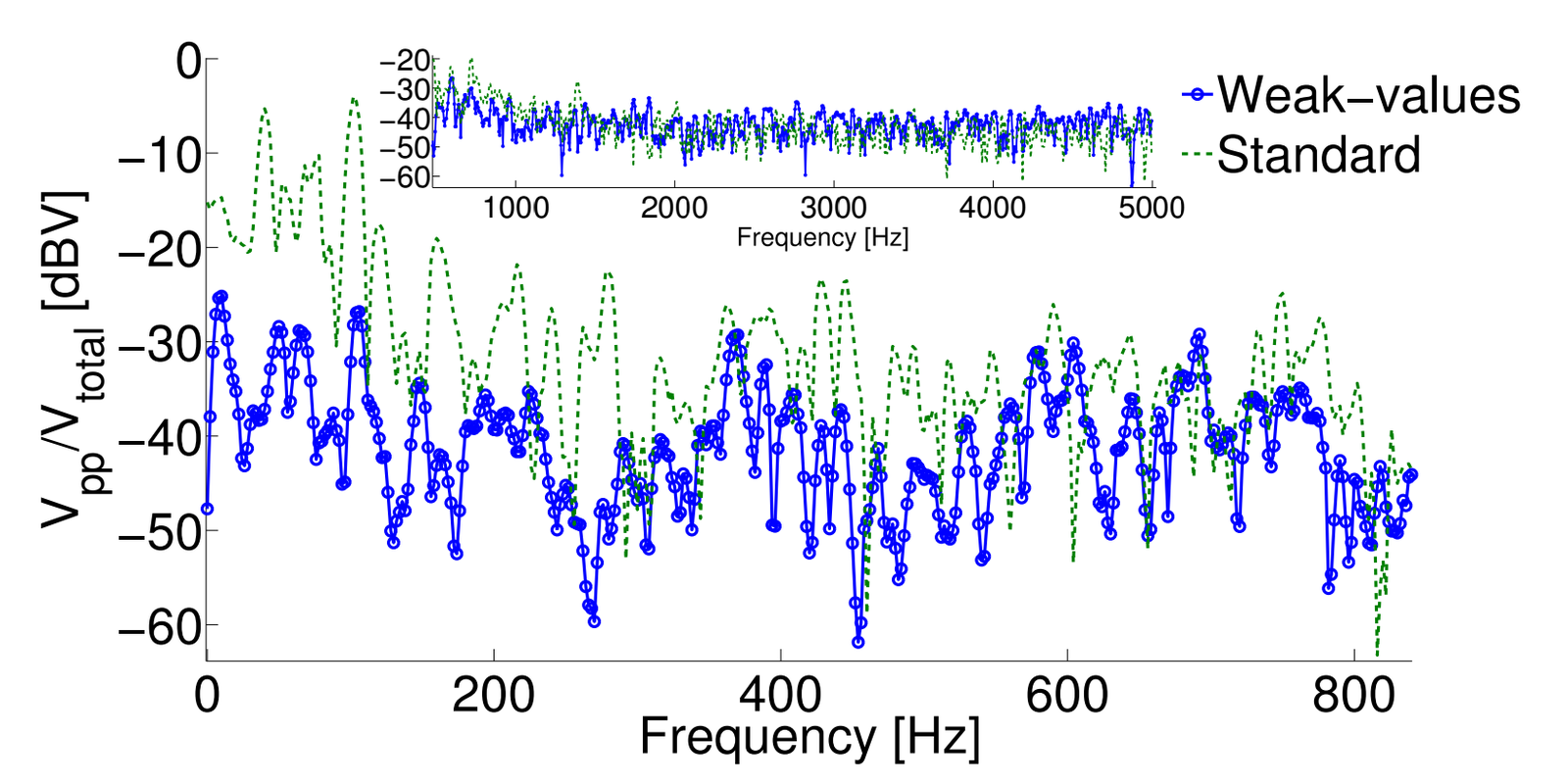
(Real noise in the wild)

Frequency Measurement

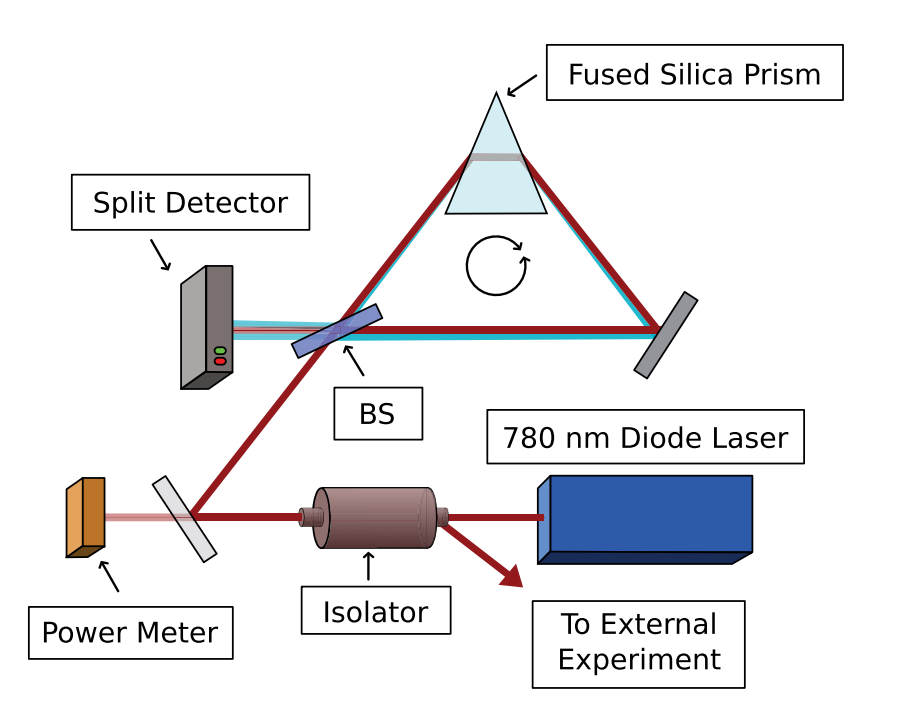
Mirror vertically misaligned to produce phase shift

\phi

Frequency-dependent horizontal tilt

Frequency-modulated and power-locked source laser

Prototype experiment: Howell lab, Rochester,  PRA 82, 063822 (2010)

Idea: Use prism to convert frequency modulation into beam tilt

Frequency to Tilt/Phase

\theta_0
\theta(f)
n(f) \ll fn'(f)
\sin\theta(f) = n(f)\sin\theta_0
\Delta\theta = \textstyle \frac{\sin\theta_0}{\cos\theta(f)} \displaystyle n'(f) \Delta f \propto \frac{c}{v_g}\frac{\Delta f}{f} \approx \frac{k}{k_0}
v_g = \frac{d\omega}{dk_0} = \frac{c}{n(f) + fn'(f)} \approx \frac{c}{fn'(f)}

Tilt from frequency dither:

(slower light amplifies tilt)

Phase if CW and CCW paths have different propagation L in prism:

\phi = \Delta L\,k_0 = 2\pi\frac{\Delta L}{c}fn(f)
\Delta \phi = 2\pi\frac{\Delta L}{c}(n(f)+fn'(f))\Delta f = \displaystyle \frac{2\pi\Delta L}{v_g} \Delta f

Frequency Results

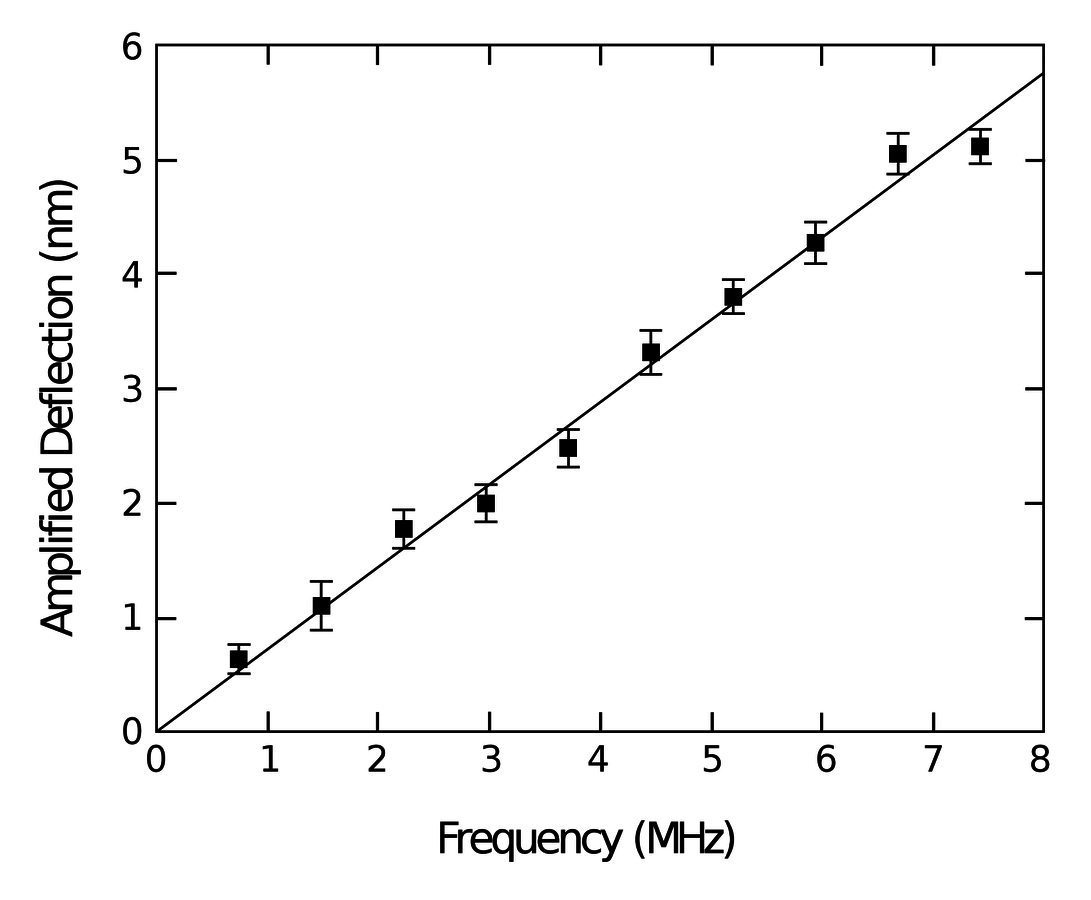
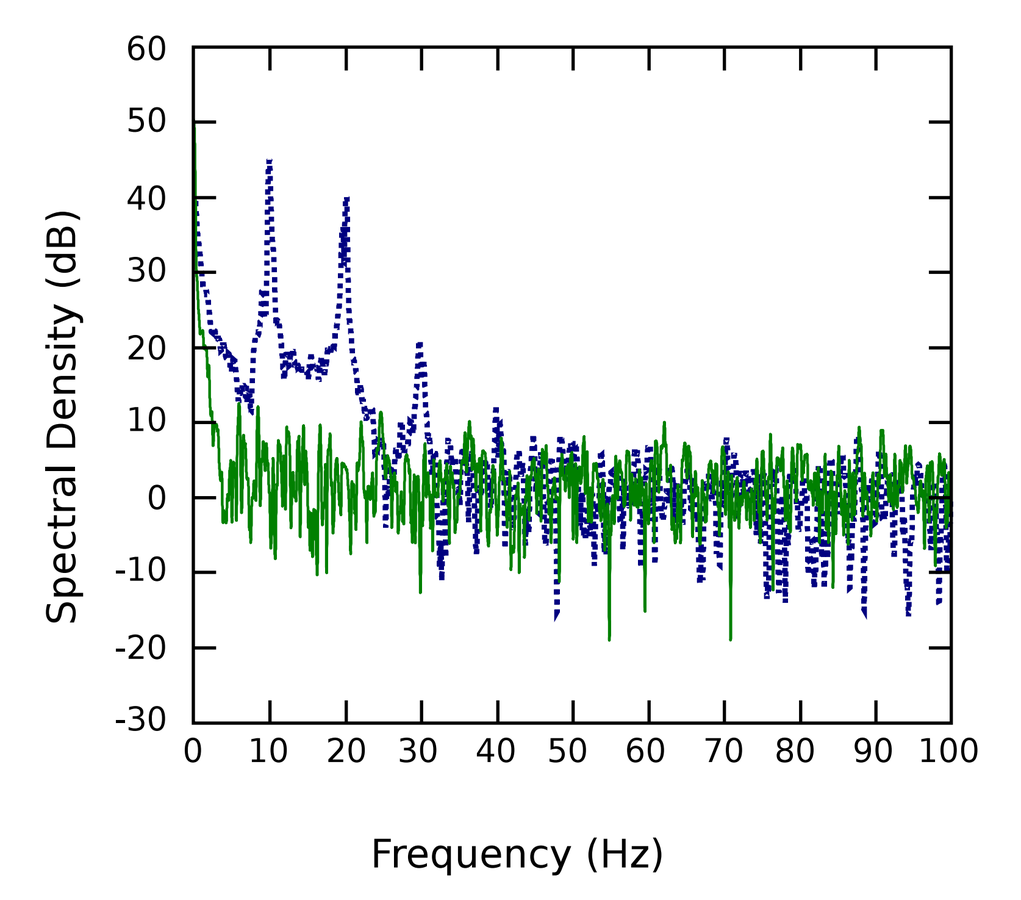
  • 780nm light (frequency                      ),  2mW CW power
  •                                         shift detected over 100ms
  • Frequency sensitivity of 
  • 10 Hz frequency modulation 35dB above noise floor
f = 340 \mathrm{THz}
\Delta f = 743 \mathrm{kHz} \approx 10^{-9} f
129 \pm 7 \mathrm{kHz}/\sqrt{\mathrm{Hz}}

Split-detection

maximum excursion

(weak value regime)

Spectral density of split detected signal

Outline

  • WVA: Tilt-sensitive Sagnac interferometer
    • Weak value analysis
    • Exact collimated analysis
    • Propagation effects
    • Noise tests
    • Frequency measurement
  • WVA: Phase-sensitive Sagnac interferometer
    • Displaced Sagnac design
    • Inverse weak value regime response
  • WVA: Remote Sensing Applications
    • Shot noise simulations with low flux
    • Speckle simulations with mode distortion

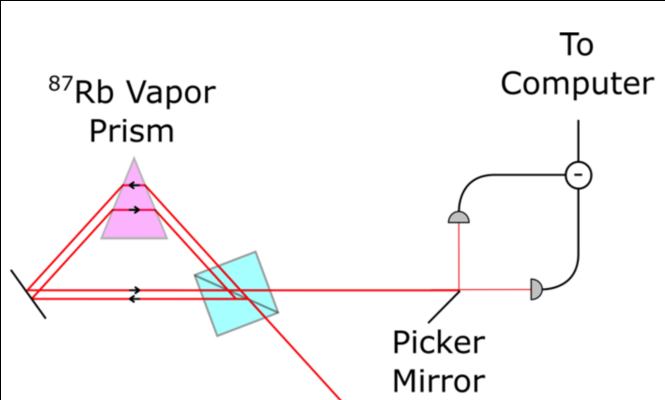
Displaced Sagnac

\theta_0
\theta(f)
n(f) \ll fn'(f)
\Delta\theta \propto \displaystyle \frac{c}{v_g}\frac{\Delta f}{f} \approx \frac{k}{k_0}
\Delta \phi = \displaystyle \frac{2\pi\Delta L}{v_g} \Delta f

More sensitive to phase

(less tilt)

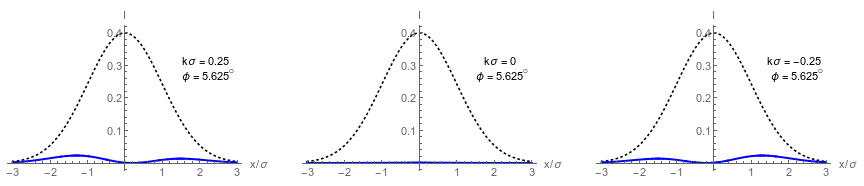
Operates in double-lobe regime (inverse weak value)

Split-detection Response

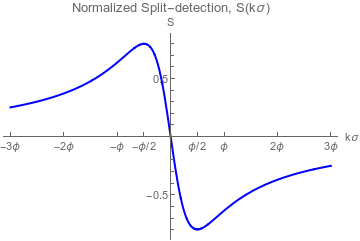
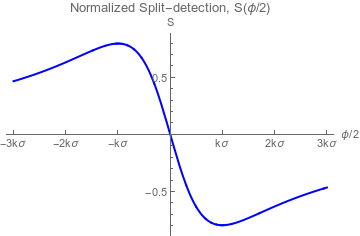
(Parameter-invariant response curves)

\phi/2
k\sigma
k\sigma \ll \phi/2 \ll 1
\phi/2 \ll k\sigma \ll 1

Weak value Regime:

Single-lobe response

Well-analyzed

Inverse Weak value Regime:

Double-lobe response

Lab tests suggest better

noise performance

Outline

  • WVA: Tilt-sensitive Sagnac interferometer
    • Weak value analysis
    • Exact collimated analysis
    • Propagation effects
    • Noise tests
    • Frequency measurement
  • WVA: Phase-sensitive Sagnac interferometer
    • Displaced Sagnac design
    • Inverse weak value regime response
  • WVA: Remote Sensing Applications
    • Shot noise simulations with low flux
    • Speckle simulations with mode distortion

Shot Noise Robustness

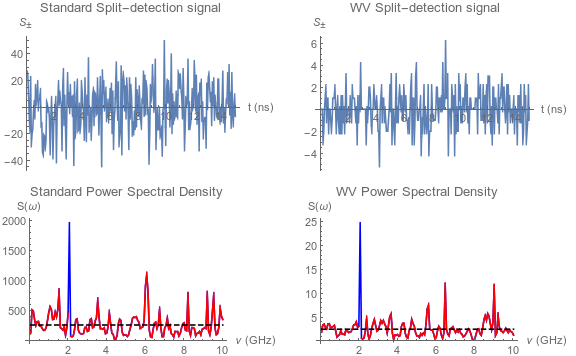
Consider one 1.2W pulse, returning ~2600 photons per modulation cycle.  After post-selection, WV has only ~26 photons remaining per cycle.

Very small FM signal is still just observed above shot noise.

The WV technique performs equally well as lens focusing.

Laser Speckle

Speckle arises from propagation of spatially random phases jumps acquired from reflection off the target, as well as turbulent propagation through the atmosphere

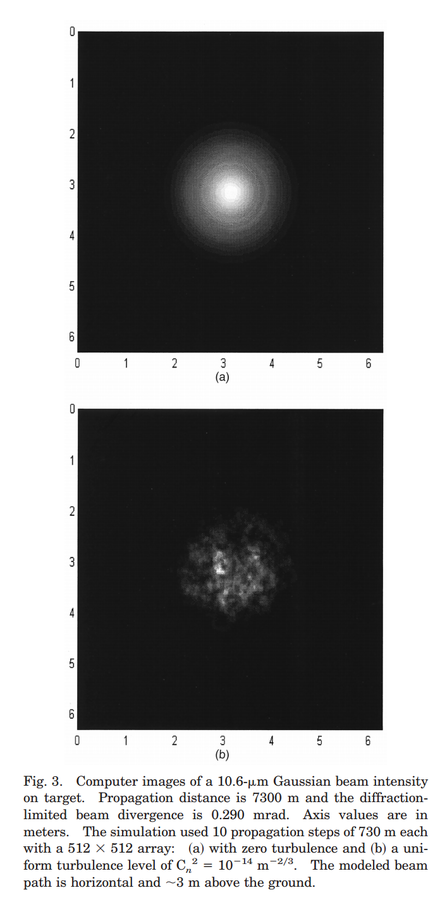
App. Opt. 39, 1857 (2000).

Speckle deteriorates the transverse spatial profile of the collected beam entering the WV interferometer 

Since the WV amplification effect relies on spatial interference, this causes concern

\langle \vec{x} |\psi(z+dz)\rangle \to \langle \vec{x} | e^{-i\hat{\vec{p}}\cdot\hat{\vec{p}}\, dz/2k_0}e^{i\theta(\hat{\vec{x}},z)} | \psi(z) \rangle

Accurate speckle can be modeled by a succession of sub-Rayleigh-length propagations dz of the transverse profile with random spatial phase screens (jumps) at each propagation length

Propagation Simulation

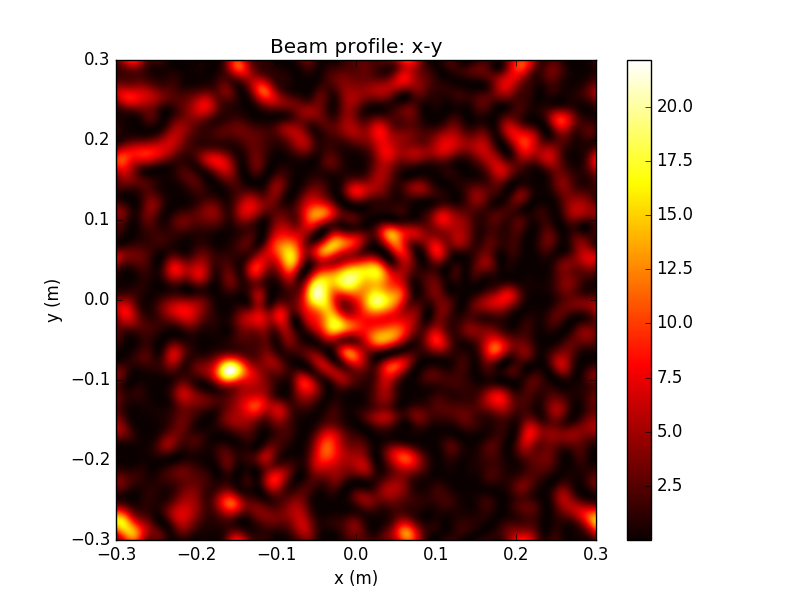
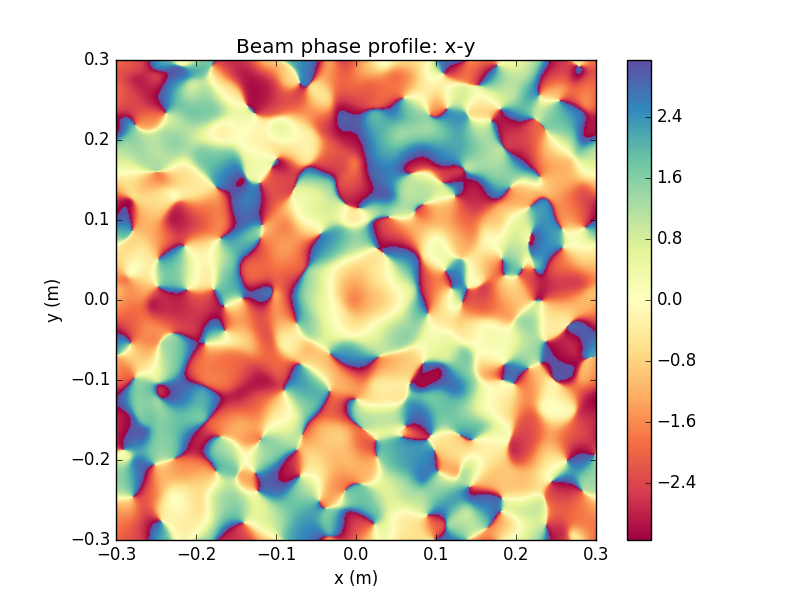
Using this technique, we can generate realistic beam profiles with fluctuating distortions in both the transverse mode profile and the phase fronts of the beam

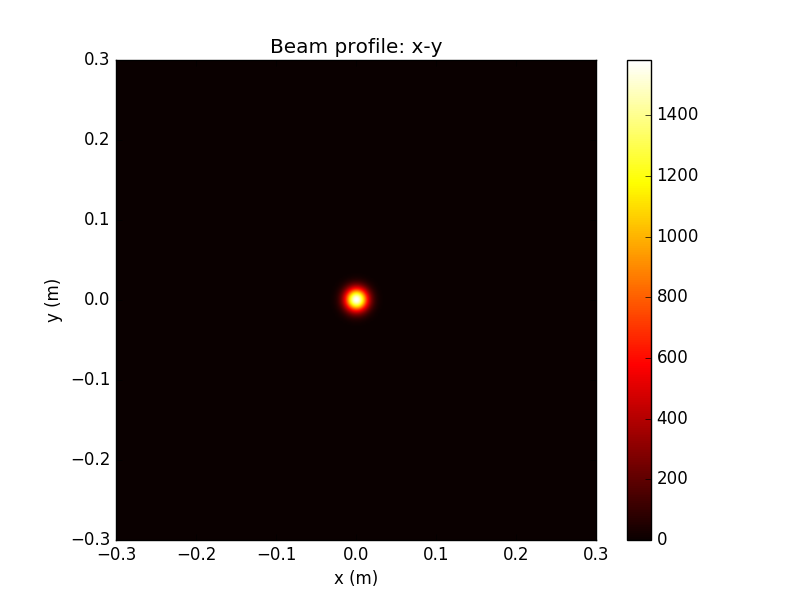
Gaussian source beam

Beam after propagation

Above: extreme example of speckle for test purposes

Note attenuation of peak by factor of 700

Propagated Beam Detail

These irregular transverse mode profile and phase fronts fluctuate in time, and will be collected by the receiving aperture and sent into the WV interferometer for filtering

 

This is an extreme non-Gaussian example

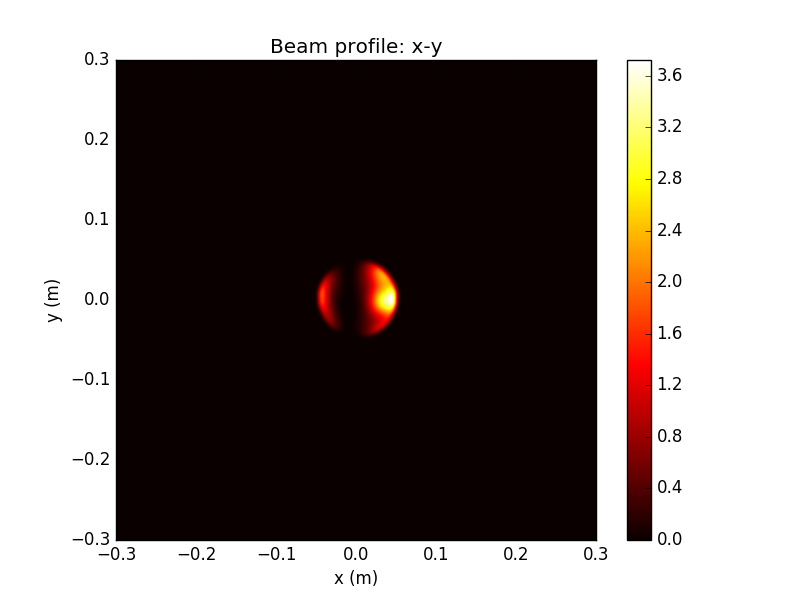
WV-filtered Beam Detail

Remarkably, after collection by an aperture (radius 5cm here), and propagation through the interferometer and out the dark port, the interference pattern at the output is almost unaffected by the irregularities of the beam

WV Attenuation: factor of ~100 from input, similar to ideal case

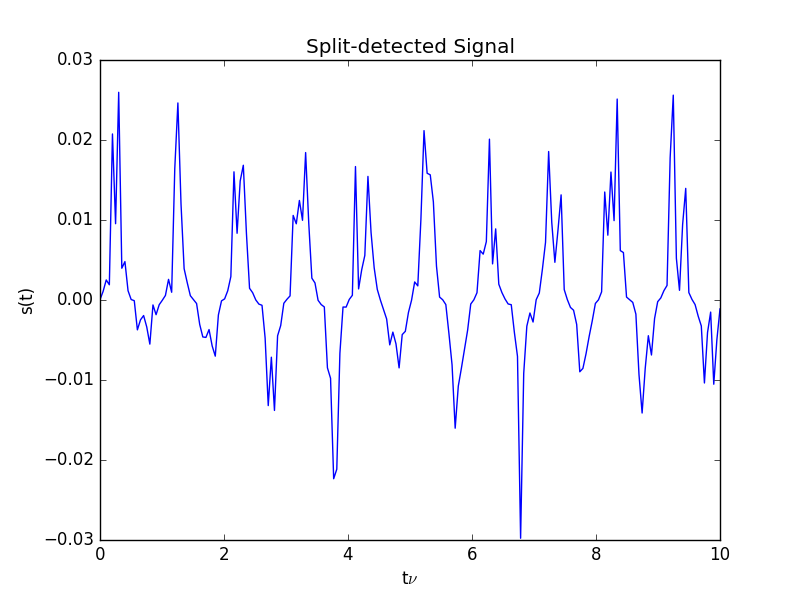
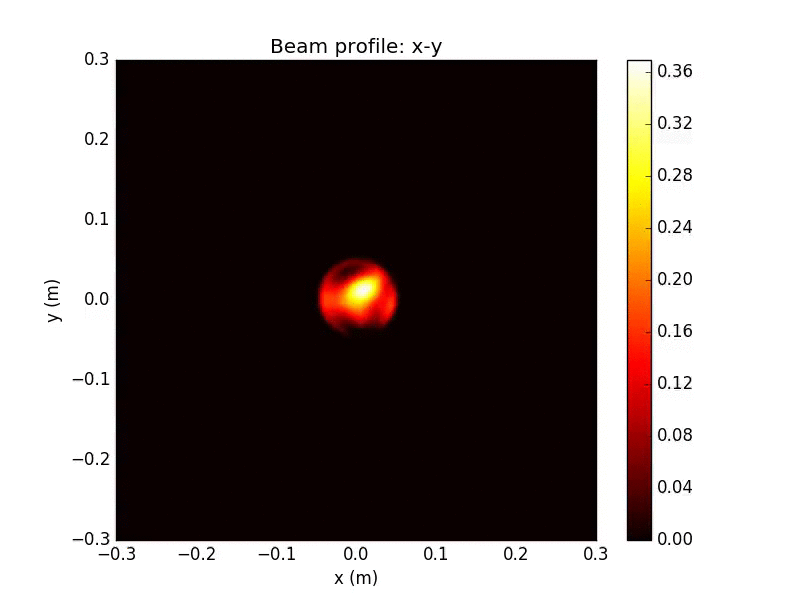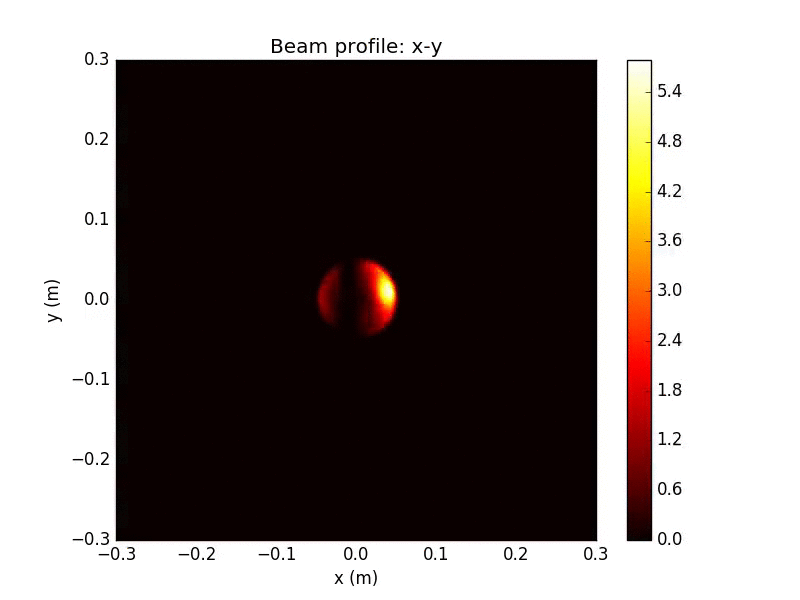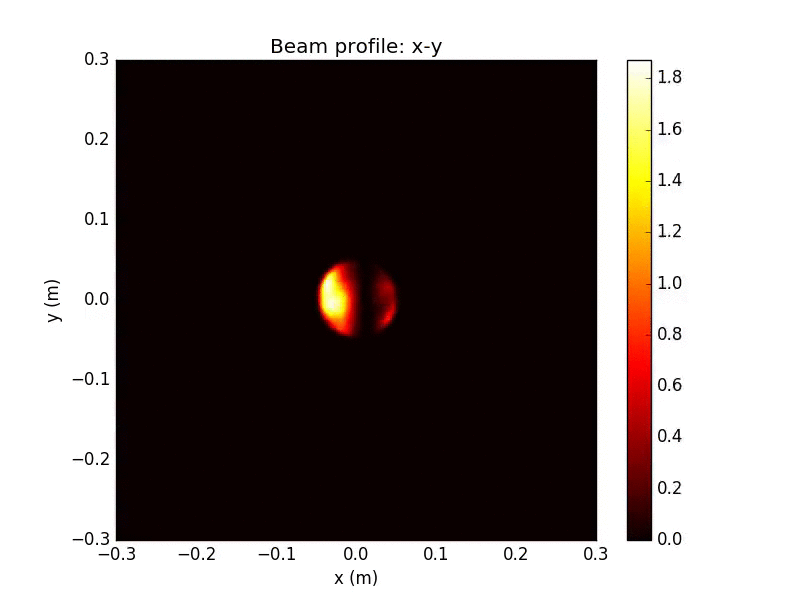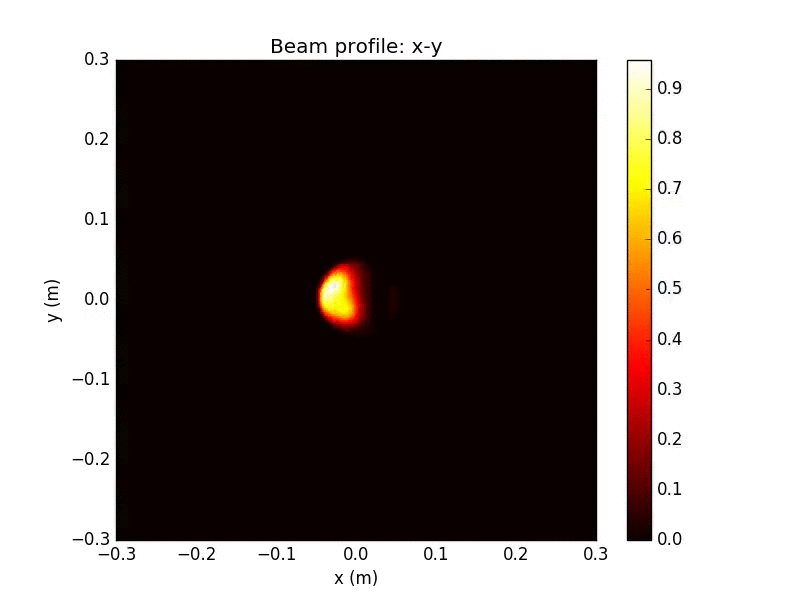
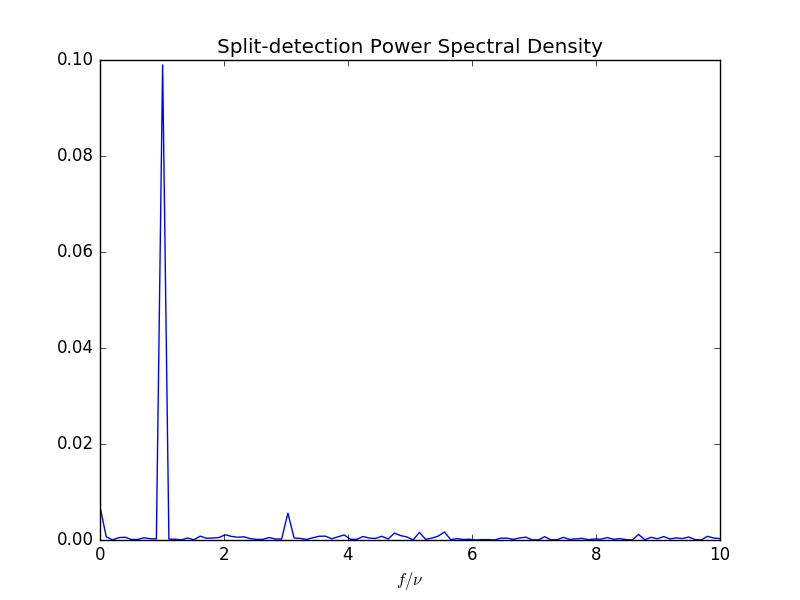
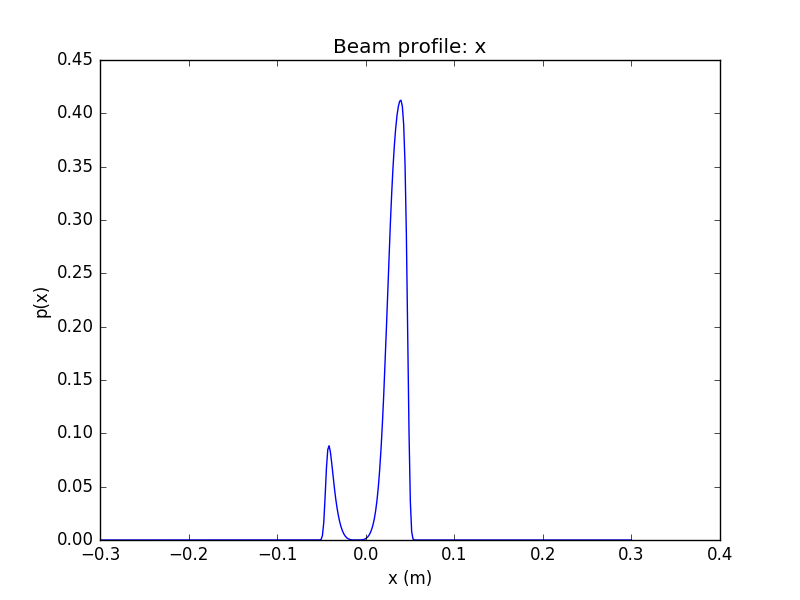
WV-filtered Split Detection

Even extreme beam irregularities have a remarkably small effect on the fidelity of the WVA-filtered and split-detected signal

 

Despite dramatic fluctuations in time of the input beam, including transverse mode distortion and phase front jitter, the signal visibility remains nearly unaffected

Conclusions

  • It is possible to concentrate all relevant information about a parameter into a small subset of events, which can be picked out by a suitable filter:  WVA achieves this!
     
  • Benefits: Can use cheaper equipment and more sensitive detectors that would saturate more easily otherwise, etc.
     
  • WVA suppresses technical noise originating outside interferometer by only amplifying inside interactions
     
  • WVA has optimal shot-noise peformance
     
  • WVA robust against transverse mode and phase distortion

Thank You!