H transport modelling with FESTIM

An open-source python-based finite elements code for hydrogen transport ​

2022

2019

Start of FESTIM development

  • 1D/2D/3D
  • Finite elements
  • Python
  • multi-material
  • Heat transfer

History of FESTIM

FESTIM open-source

  • development continuing at MIT

Oct 2023

v1.0 release

2024

FESTIM

\rho C_p \frac{\partial T}{\partial t} = \nabla \cdot (\lambda \nabla T)
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}

Hydrogen transport

Heat transfer

diffusion and trapping

McNabb & Foster

An open-source python-based finite elements code for hydrogen transport ​

FESTIM

An open-source python-based finite elements code for hydrogen transport ​

  • Based on the FEniCS library
  • Flexible
  • Complex geometries
  • Very well established library

FESTIM

Check it out on Github

github.com/festim-dev/FESTIM

✅ More transparency

✅ More collaborations

✅ More flexibility

An open-source python-based finite elements code for hydrogen transport ​

The code is missing a feature?

Just add it!

Found a bug?

Report it and we'll fix it!

📈5 years of development

📑12+ publications

🗣️100+ citations

🧑‍💻14+ contributors

🏛️20+ institutions using the code

🧑‍💻27+ Slack members

⭐75+ stars on GitHub

      3 workshops

FESTIM in numbers

Evolution of GitHub stars

FESTIM is used worldwide

8 private companies

10 universities

16 research organisations

FESTIM

  • Easy to learn
  • Plenty of libraries (numpy, scipy, matplotlib, HTM...)

An open-source python-based finite elements code for hydrogen transport ​ 

conda install -c conda-forge fenics
pip install festim

Two lines to install!

import festim as F
import numpy as np

my_model = F.Simulation()

my_model.mesh = F.MeshFromVertices(
    vertices=np.linspace(0, 1e-6, num=1001)
)


my_model.materials = F.Material(id=1, D_0=1.9e-7, E_D=0.2)

my_model.T = F.Temperature(500)  # K

my_model.boundary_conditions = [
    F.DirichletBC(
        surfaces=[1, 2],
        value=1e15,   # H/m3/s
        field=0
        )
]

my_model.settings = F.Settings(
    absolute_tolerance=1e10,
    relative_tolerance=1e-10,
    final_time=100  # s
    )


my_model.dt = F.Stepsize(0.1)  # s

my_model.initialise()

my_model.run()

Simple simulation

Make use of the python ecosystem

Create a 1D mesh easily

Materials

Temperature

Boundary conditions

Settings and stepsize

Only a few lines of python!

FESTIM is fully documented

Check out the complete documentation at

festim.readthedocs.io

Installation instructions

User guide

FESTIM's philosophy

We want to make hydrogen transport simulations easy for everyone!

 

We also encourage contributions!

  • Feedback (suggestions, bug reports...)
  • Implement new features
  • Bug fixing
  • Documentation update (even small ones!)
  • ...

Look out for "Good first issues"

on GitHub

Gallery of examples

Thermo-desorption

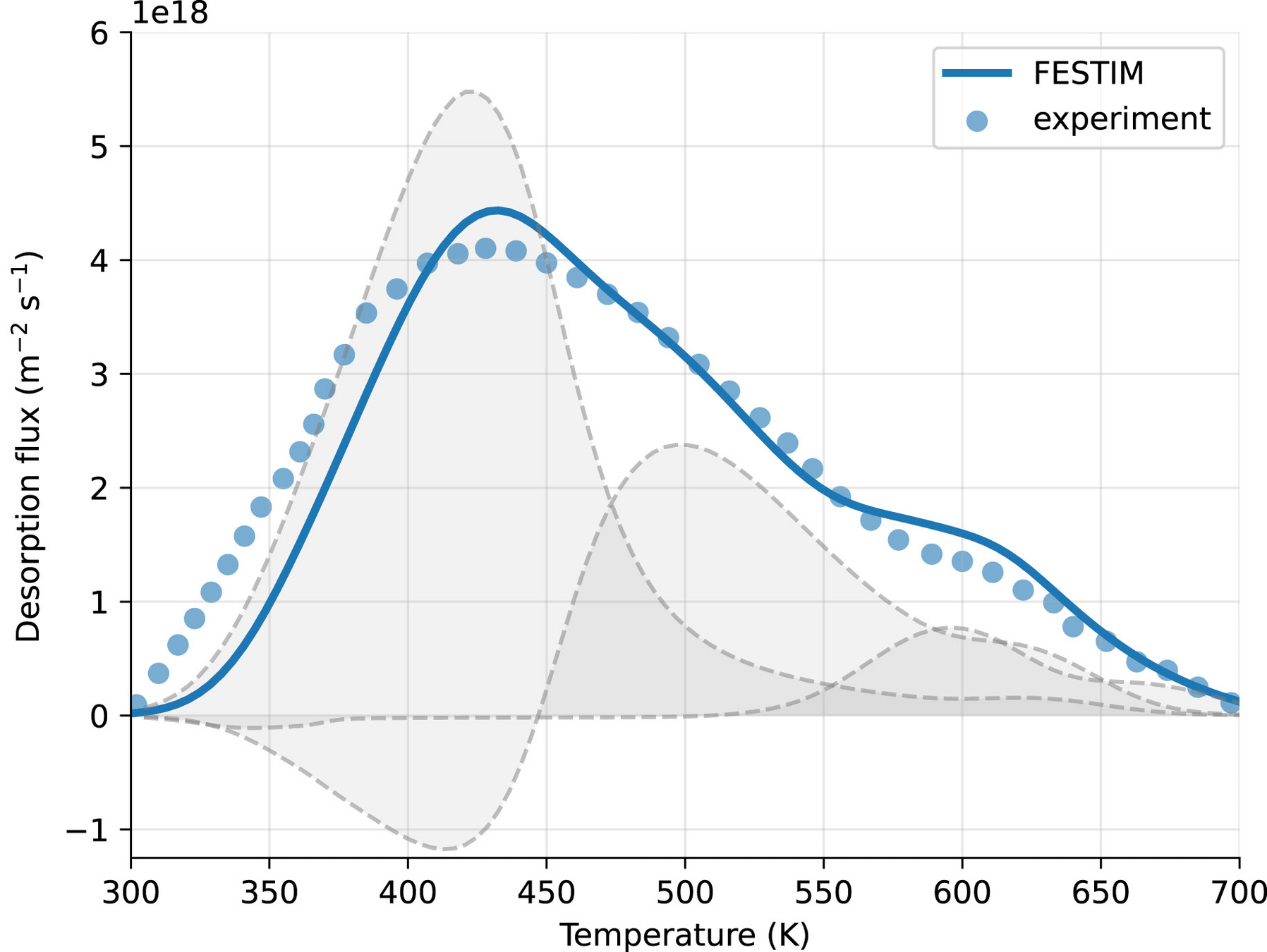
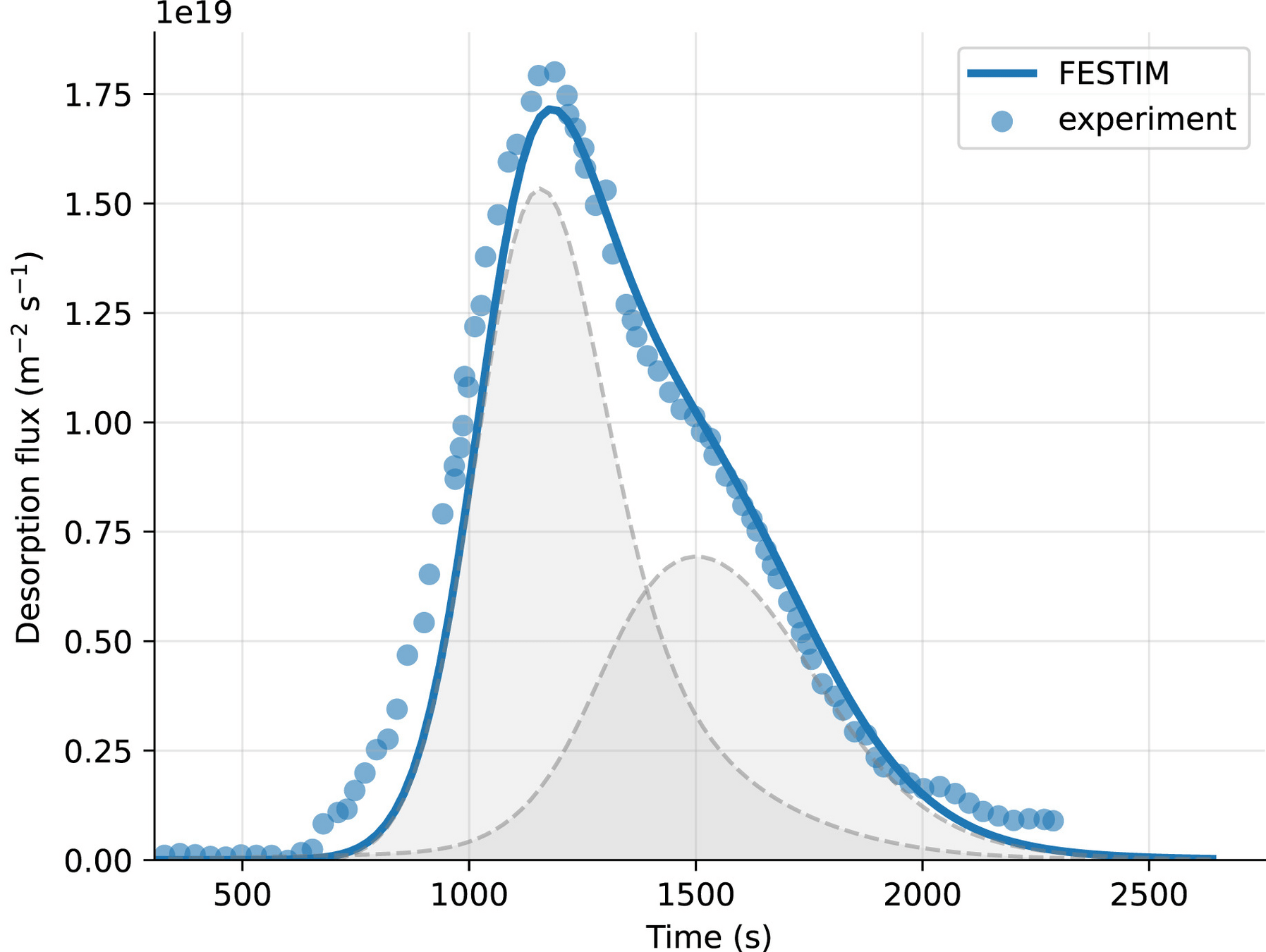
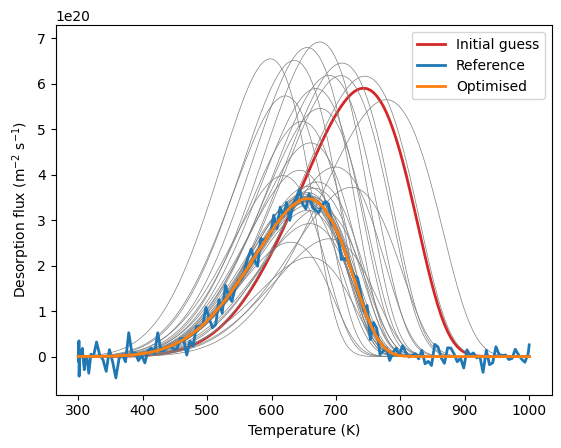
  • TDS analysis
  • Automated fitting routines

Permeation experiment

No barrier

with barrier

Permeation barrier

Substrate

High H pressure

Low H pressure

Conservation of chemical potential

Permeation flux

\frac{c^-}{K_S^-} = \frac{c^+}{K_S^+}

Super-permeation

  • H is implanted in the first \( 10 \ \mathrm{nm} \)
  • Super-permeation regime is attained at high recombination energy (upstream surface)
  • Source code

Benedikt & Day, (2017) Fusion Engineering and Design

3D ITER monoblock

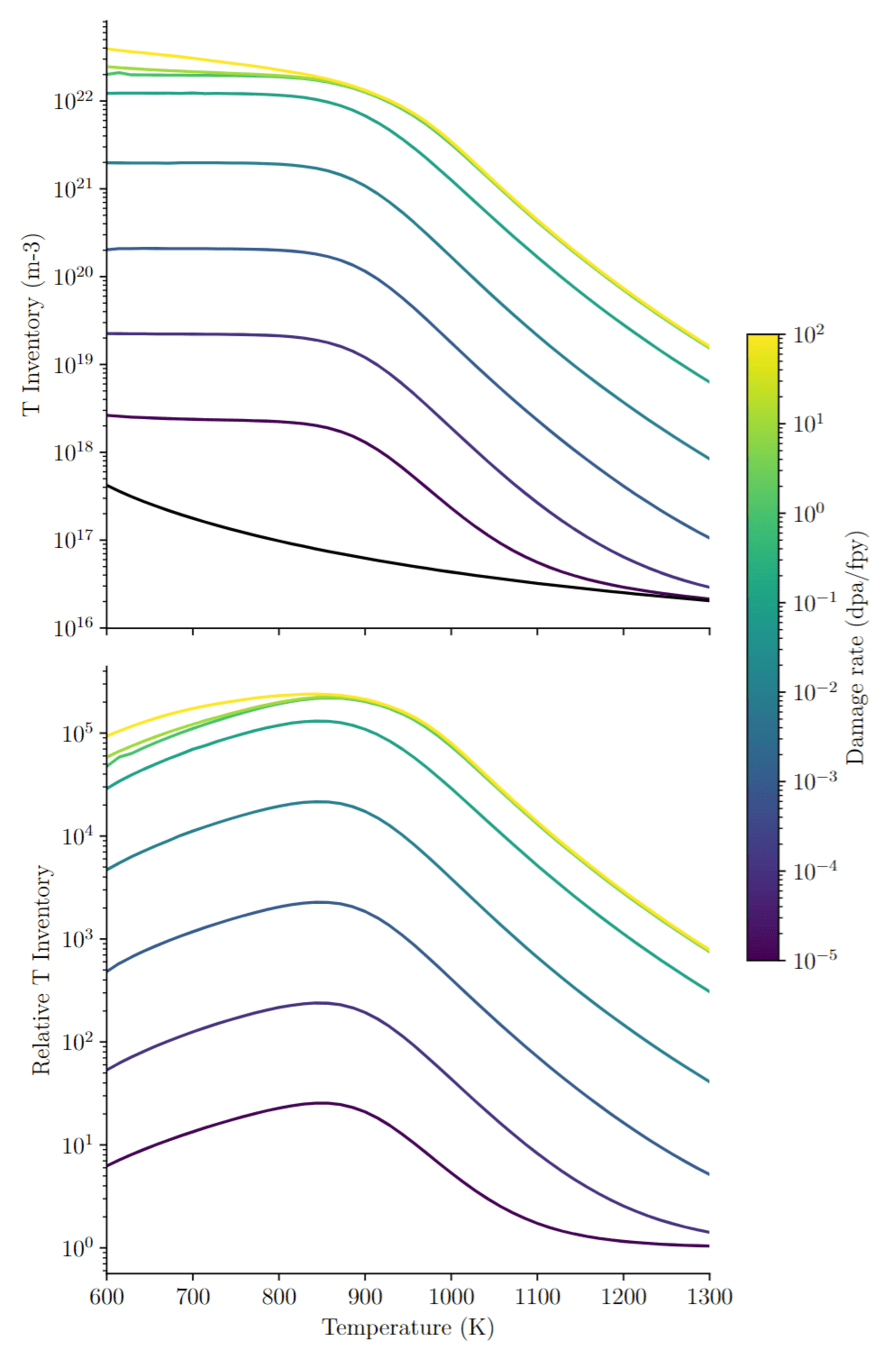
  • Delaporte-Mathurin et al 2024 International Journal of Hydrogen Energy 63 786–802
  • Delaporte-Mathurin et al 2024 Nucl. Fusion 64 026003
  • Transient estimation of tritium retention
  • Multi-material
  • Heat transfer

Influence of ELMs on retention

courtesy of V. Kulagin (MePhi)

  • 1D model of a ITER monoblock
  • Transient heat transfer simulation
  • Varying surface heat flux

Breeding Blanket

courtesy of J. Dark (CEA/LSPM)

  • Complex 3D geometry
  • Coupled to fluid dynamics
  • Tritium generation in the breeder volume

James Dark et al 2021 Nucl. Fusion 61 116076

Neutron-induced trap model

  • Custom trap model
  • Dynamic evolution of trap densities including annealing
  • Parametrised on TDS data from T Schwartz Selinger

courtesy of J. Dark (CEA LSPM)

Tritium extraction system

courtesy of K. Dunnell (MIT)

  • Complex 3D geometry
  • Coupled with fluid dynamics
  • Tritium extraction from permeable membranes

BABY breeding experiment

Velocity

Temperature

Tritium concentration

courtesy of C. Weaver (MIT)

① neutrons are generated

 

② tritium is created from nuclear reactions

 

③ tritium is transported in the salt

 

④ tritium is released into the gas phase

 

⑤ tritium is collected and counted

Our tritium breeding experiment

Kinetic surface model

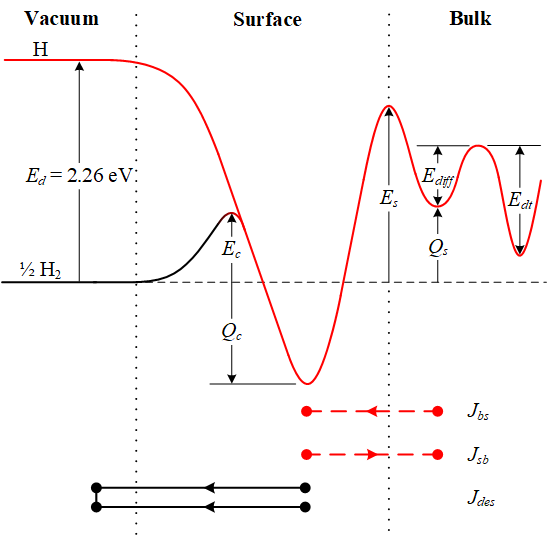
courtesy of V. Kulagin (MePhi)

Depleting enclosure

\(P(t)\)

permeation flux

Enclosure

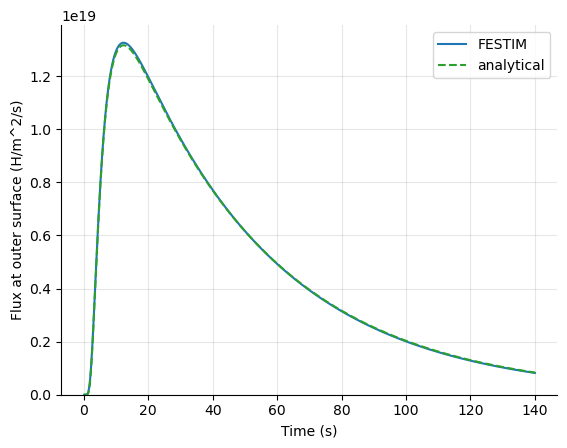
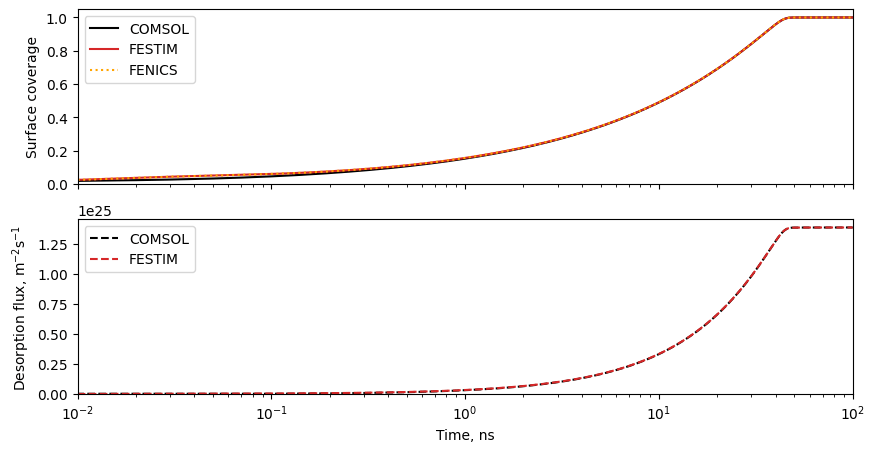
\frac{dP(t)}{dt} \propto \varphi_\mathrm{permeation}\\ \varphi_\mathrm{permeation} \propto P(t)

FESTIM is thoroughly tested, verified, and validated

  • Validated against TDS, permeation experiments...
  • Verified against analytical solutions in many different problems
  • Check out FESTIM's V&V book online! (WIP)

festim-vv-report.readthedocs.io

 

V&V

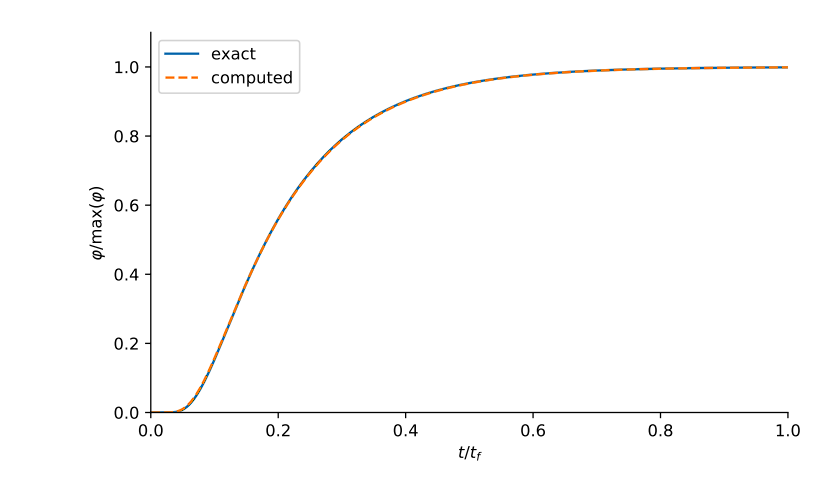
Effective-diffusion through a slab

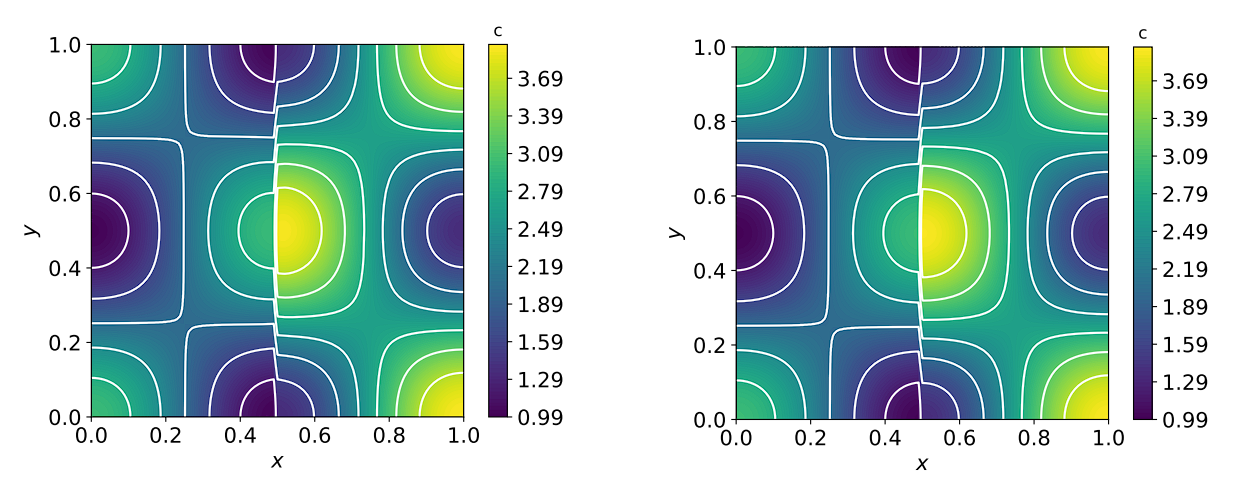
2D multi-material

Exact

Computed concentration

Method of Exact Solution

governing equations

exact solutions

parameters (sources, BCs, ICs)

FESTIM

computed solutions

solve

run

compare

⚠️sometimes very complex!

Method of Manufactured Solutions

governing equations

manufactured solutions

source terms, BCs and ICs

FESTIM

computed solutions

compare

FESTIM's development workflow

  • Anyone can create their own copy (fork) of the FESTIM repository and make changes
  • PRs are a place where FESTIM's maintainers review the proposed changes
  • ~500 tests are automatically run
  • The PR is only merged when all the tests pass ✅

fork

fork

pull request

FESTIM

Jane Doe

FESTIM

John Doe

FESTIM

festim-dev

pull request

How to use FESTIM

github.com/festim-dev/festim

User-support forum

festim.discourse.group

User-support forum

Join the Slack channel

Documentation

and installation instructions

festim.readthedocs.io

FESTIM workshop

The FESTIM workshop is a series of tutorials

 

from basic problems to more advance cases

festim.discourse.group

A glimpse into the future

Towards FESTIM2

Core changes

conda install -c conda-forge fenics-dolfinx
pip install git+https://github.com/festim-dev/festim.git@fenicsx
  • upgrade of the finite element engine → dolfinx
  • Better handling of interfaces (WIP)
  • Support for multi-species
  • Better parallel scalability
  • Implementation of Reaction

You can try this version of FESTIM right now!

New examples

Multi-isotope, multi-level trapping

  • 7 different species
  • 6 reactions
  • \( c_H = 10^{20} \ \mathrm{m^{-3}} \) on the left
  • \( c_D = 10^{19} \ \mathrm{m^{-3}} \) on the right
  • Source code available here

1 trap, 2 levels, 2 isotopes

\mathrm{H} + [\ \ \ ] \ \substack{p_1 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_1} \ [\mathrm{H}_1\mathrm{D}_0]
\mathrm{H} + [\mathrm{H}_1\mathrm{D}_0] \ \substack{p_2 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_2} \ [\mathrm{H}_2\mathrm{D}_0]
\mathrm{D} + [\ \ \ ] \ \substack{p_3 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_3} \ [\mathrm{H}_0\mathrm{D}_1]
\mathrm{D} + [\mathrm{H}_0\mathrm{D}_1] \ \substack{p_4 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_4} \ [\mathrm{H}_0\mathrm{D}_2]
\mathrm{H} + [\mathrm{H}_0\mathrm{D}_1] \ \substack{p_5 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_5} \ [\mathrm{H}_1\mathrm{D}_1]
\mathrm{D} + [\mathrm{H}_1\mathrm{D}_0] \ \substack{p_6 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_6} \ [\mathrm{H}_1\mathrm{D}_1]

\( \mathrm{H} \) = mobile H

\( \mathrm{D} \) = mobile D

\( [\mathrm{H}_x\mathrm{D}_y] \) = \(x\) H and \(y\) D in trap

Isotope swapping

\mathrm{H} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{H}]_\mathrm{trap}
\mathrm{D} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{D}]_\mathrm{trap}
\mathrm{D} + [\mathrm{H}]_\mathrm{trap} \ \substack{k_\mathrm{swap} \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1.2em] k_\mathrm{swap}} \ [\mathrm{D}]_\mathrm{trap} + \mathrm{H}

same underlying equations!

Can be represented by festim.Reaction

Isotope swapping

my_model.species = [
    mobile_H,
    mobile_D,
    trapped_H,
    trapped_D,
]

my_model.reactions = [
    F.Reaction(
        k_0=k_0,
        E_k=0.39,
        p_0=1e13,
        E_p=1.2,
        reactant1=mobile_H,
        reactant2=empty_trap,
        product=trapped_H,
        volume=my_subdomain,
    ),
    F.Reaction(
        k_0=k_0,
        E_k=0.39,
        p_0=1e13,
        E_p=1.2,
        reactant1=mobile_D,
        reactant2=empty_trap,
        product=trapped_D,
        volume=my_subdomain,
    ),
    F.Reaction(
        k_0=k_0,
        E_k=0.1,
        p_0=k_0,
        E_p=0.1,
        reactant1=mobile_H,
        reactant2=trapped_D,
        product=[mobile_D, trapped_H],
        volume=my_subdomain,
    ),
]

Usual trapping reactions

Swapping reaction

4 species are defined

Spherical cavity trapping

see Zibrov and Schmid, NME, 2024

for complete description

  • Implementation in FESTIM of the spherical cavity trapping model developed by Zibrov and Schmid
  • Custom trapping equations
  • Smooth implementation in FESTIM

Anisotropy

  • Anisotropic materials can be simulated with very few modifications
D = \begin{bmatrix} D_{xx} & 0\\ 0 & D_{yy} \end{bmatrix}

Follow the development roadmap

github.com/orgs/festim-dev/projects/2