FESTIM: overview of hydrogen transport simulation capabilities

Remi Delaporte-Mathurin and FESTIM contributors

User inputs

  • Material properties
  • Trap properties
  • Geometry
  • Boundary conditions
  • Initial conditions
  •            ...
T

FESTIM

Outputs

  • H concentration fields \(c(x,t)\)
  • Temperature field \(T(x,t)\)
  • surface fluxes
  • inventories
  • average concentration
  •              ...

Heat transfer model

Hydrogen transport model(s)

Delaporte-Mathurin et al, 2024. International Journal of Hydrogen Energy 10.1016/j.ijhydene.2024.03.184

📈5 years of development

📑14+ publications

🗣️130+ citations

🧑‍💻23+ contributors

🏛️27+ institutions using the code

🧑‍💻80+ Slack members

⭐~100 stars on GitHub

🧑‍💻4 user workshops

FESTIM in numbers

✅100% open-source

Source code: github.com/festim-dev/FESTIM

Tutorials: github.com/festim-dev/FESTIM-workshop

Documentation: festim.readthedocs.io

FESTIM is verified & validated

  • Validated against TDS, permeation experiments...
     
  • Verified against analytical solutions in many different problems
     
  • New V&V online book

festim-vv-report.readthedocs.io

 

  • 19 V&V cases in total (more to come)

Remi Delaporte-Mathurin and Jair Santana, FESTIM V&V Book, 2024, https://dspace.mit.edu/handle/1721.1/156690.

FESTIM from mesoscale to reactor scale

Gas driven permeation

J_\mathrm{left} = K_d \ P - K_r \ c^2
J_\mathrm{right} = - K_r \ c^2

Surface limited regime

Bulk limited regime

Transition to bulk limited as the permeation number \( W \) increases

High H pressure

Low H pressure

Permeation flux

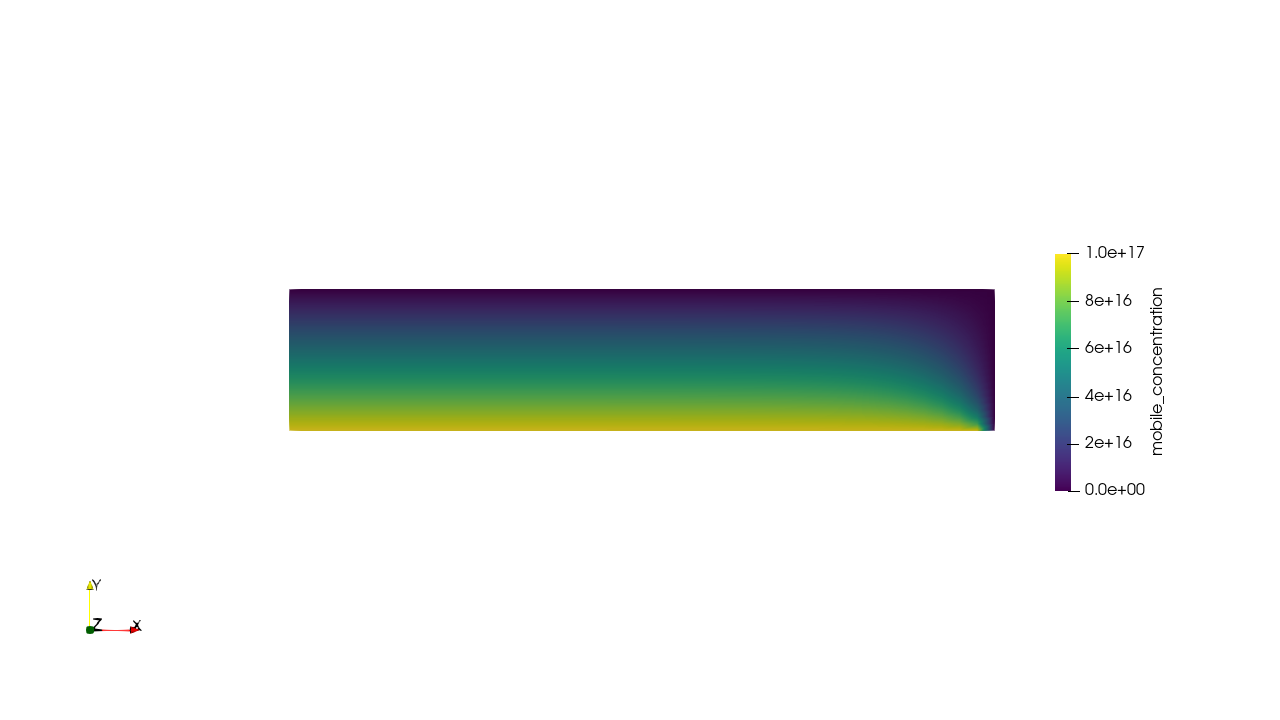
\( c = K_H \ P_\mathrm{up} \)

\( c = 0 \)

Permeation through the crucible wall

FLiBe

2D permeation through molten salts

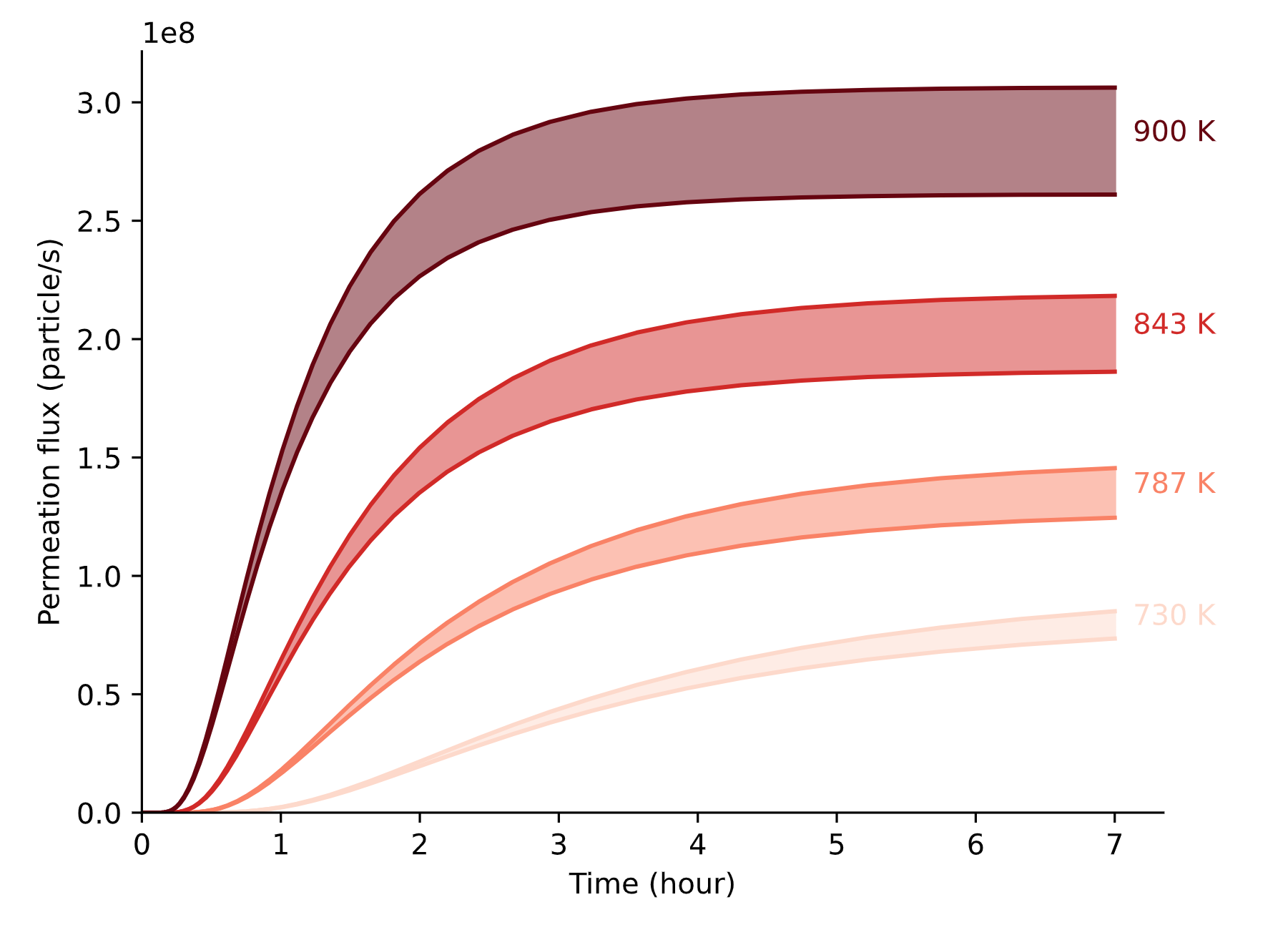
\mathrm{flux} = 2 \pi \ \int_0^R r \ D \nabla c \ \cdot \mathbf{n} \ dr

HYPERION permeation rig

Permeation barriers

No barrier

with barrier

Permeation barrier

Substrate

High H pressure

Low H pressure

Permeation flux

Ongoing tritium permeation barriers development project at MIT

Conservation of chemical potential

\frac{c^-}{K_S^-} = \frac{c^+}{K_S^+}

TDS analysis: neutron damage

 James Dark et al 2024 Nucl. Fusion 64 086026

\frac{d n}{dt} = \Phi \ K \ (1 - \frac{n}{n_\mathrm{max}}) - A \ n
  • New proposed model for neutron-induced trap creation
     
  • Parameterised on TDS data (self-damaged W)

TDS analysis: neutron damage

 James Dark et al 2024 Nucl. Fusion 64 086026

  • Model was used to simulate inventory evolution in PFCs
     
  • Neglecting neutron traps could potentially underestimate inventories by several orders of magnitude after 1 FPY
     
  • Need similar studies for structural materials!

TDS analysis: codeposits

Patino et al. Nuclear Materials and Energy 41 (2024) 101808

  • Simulation of W codeposited layers
     
  • Influence of partial pressure
     
  • 10 different traps!

Kinetic surface model

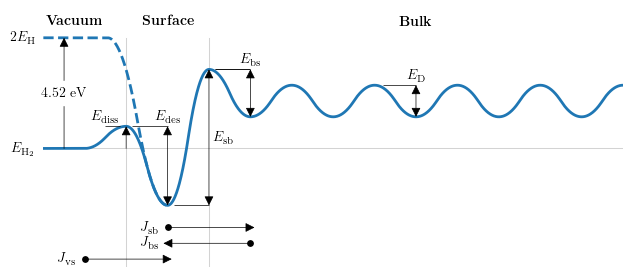
Kulagin et al (2024) arXiv, arXiv:2411.16474

Kinetic surface model

V&V available at
github.com/KulaginVladimir/FESTIM-SurfaceKinetics-Validation

Kulagin et al (2024) arXiv, arXiv:2411.16474

  • D in damaged W (S. Markelj JNM 2016)
     
  • Comparison with NRA profiles

Kinetic surface model

V&V available at
github.com/KulaginVladimir/FESTIM-SurfaceKinetics-Validation

Kulagin et al (2024) arXiv, arXiv:2411.16474

  • H in oxidised W (A. Dunand et al 2022 Nucl. Fusion)
     
  • Comparison with TDS spectra

Kinetic surface model

V&V available at
github.com/KulaginVladimir/FESTIM-SurfaceKinetics-Validation

Kulagin et al (2024) arXiv, arXiv:2411.16474

  • H in Ti (Hirooka et al 1981 JNM)
     
  • Validation at 5 temperatures

H content (H/Ti)

Component scale modelling & multiphysics

Influence of ELMs on retention

Kulagin, V., & Gasparyan, Y. Numerical Simulation of deuterium retention in tungsten under ELM-like conditions. J. Nucl. Mater.

  • 1D model of a ITER monoblock
     
  • Transient heat transfer simulation
     
  • Varying surface heat flux

Metal Foil Pumps for DIR

  • H is implanted in the first \( 10 \ \mathrm{nm} \)
  • Super-permeation regime is attained at high recombination energy (upstream surface)
  • Source code

Benedikt & Day, (2017) Fusion Engineering and Design

Retention studies

  • Delaporte-Mathurin et al 2024 International Journal of Hydrogen Energy 63 786–802
  • Delaporte-Mathurin et al 2024 Nucl. Fusion 64 026003
  • ITER plasma facing components
     
  • Transient estimation of tritium retention

Retention (T/m3)

Detritiation studies

Delaporte-Mathurin et al 2024 Nucl. Fusion 64 026003

Breeding Blanket modelling

  • DEMO WCLL
  • Complex 3D geometry
  • Coupled to fluid dynamics
  • Tritium generation in the LiPb volume (computed from neutronics)

James Dark et al 2021 Nucl. Fusion 61 116076

Tritium extraction system

Dunnell and Delaporte-Mathurin, MIT NSE Beyond Oppenheimer (2024)  10.13140/RG.2.2.13923.16164

  • Permeation Against Vacuum
  • Complex 3D geometry
  • Coupled with fluid dynamics
  • Tritium extraction from permeable membranes

MIT tritium breeding experiment

Velocity

Temperature

Tritium concentration

For more details on experiment: Delaporte-Mathurin et al, Advancing Tritium Self-Sufficiency in Fusion Power Plants: Insights from the BABY Experiment  (under review in Nucl. Fusion)

① neutrons are generated

 

② tritium is created from nuclear reactions

 

③ tritium is transported in the salt

 

④ tritium is released into the gas phase

 

⑤ tritium is collected and counted

BABY breeding experiment

Towards FESTIM2

  • Rewrite of FESTIM with FEniCSx
  • Improved performances
  • New physics and features

Spherical cavity trapping

see Zibrov and Schmid, NME, 2024

for complete description

  • Implementation in FESTIM of the spherical cavity trapping model developed by Zibrov and Schmid
  • Custom trapping equations
  • Smooth implementation in FESTIM

Anisotropy

  • Anisotropic materials can be simulated with very few modifications
  • Composites
  • Anisotropic microstructures
D = \begin{bmatrix} D_{xx} & 0\\ 0 & D_{yy} \end{bmatrix}
\mathrm{H} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{H}]_\mathrm{trap}
\mathrm{D} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{D}]_\mathrm{trap}
\mathrm{D} + [\mathrm{H}]_\mathrm{trap} \ \substack{k_\mathrm{swap} \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1.2em] k_\mathrm{swap}} \ [\mathrm{D}]_\mathrm{trap} + \mathrm{H}

same underlying equations!

Can be represented by festim.Reaction

Isotope swapping

Trapping reactions

Swapping reaction

Isotope swapping

my_model.species = [
    mobile_H,
    mobile_D,
    trapped_H,
    trapped_D,
]

my_model.reactions = [
    F.Reaction(
        k_0=k_0,
        E_k=0.39,
        p_0=1e13,
        E_p=1.2,
        reactant1=mobile_H,
        reactant2=empty_trap,
        product=trapped_H,
        volume=my_subdomain,
    ),
    F.Reaction(
        k_0=k_0,
        E_k=0.39,
        p_0=1e13,
        E_p=1.2,
        reactant1=mobile_D,
        reactant2=empty_trap,
        product=trapped_D,
        volume=my_subdomain,
    ),
    F.Reaction(
        k_0=k_0,
        E_k=0.1,
        p_0=k_0,
        E_p=0.1,
        reactant1=mobile_H,
        reactant2=trapped_D,
        product=[mobile_D, trapped_H],
        volume=my_subdomain,
    ),
]

Usual trapping reactions

Swapping reaction

4 species are defined

Multi-isotope transport and multi-level trapping

  • 2 isotopes, 1 trap (2 levels)
  • 7 different species
  • 6 reactions
\mathrm{H} + [\ \ \ ] \ \substack{p_1 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_1} \ [\mathrm{H}_1\mathrm{D}_0]
\mathrm{H} + [\mathrm{H}_1\mathrm{D}_0] \ \substack{p_2 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_2} \ [\mathrm{H}_2\mathrm{D}_0]
\mathrm{D} + [\ \ \ ] \ \substack{p_3 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_3} \ [\mathrm{H}_0\mathrm{D}_1]
\mathrm{D} + [\mathrm{H}_0\mathrm{D}_1] \ \substack{p_4 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_4} \ [\mathrm{H}_0\mathrm{D}_2]
\mathrm{H} + [\mathrm{H}_0\mathrm{D}_1] \ \substack{p_5 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_5} \ [\mathrm{H}_1\mathrm{D}_1]
\mathrm{D} + [\mathrm{H}_1\mathrm{D}_0] \ \substack{p_6 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_6} \ [\mathrm{H}_1\mathrm{D}_1]

✅Mixed domain can streamline multiphysics coupling

 

❌Some methods do not work for dissimilar materials (Henry vs Sieverts)

FESTIM 2 is much faster

3-30x

faster

HISP project: coupling FESTIM to plasma codes

RISP pulse

ITER FW divided in 60 bins

Data from DINA

Goal: find the best strategy for minimising ITER T inventory

HISP project: coupling FESTIM to plasma codes

10 DT FP pulses

ICWC + RISP

GDC

Simulation time:
~ 60 s per bin (~ hour full reactor)

HISP project: coupling FESTIM to plasma codes

  • Multi isotopes
     
  • Parametrisation for W, B, SS
     
  • Testing different scenarios for detritiation in ITER
     
  • Flexible enough to be reactor-and plasma code-agnostic
     
  • Open-source development
    github.com/kaelyndunnell/hisp

Take aways

🚀FESTIM is extremely versatile, from simple to complex cases, from small scale to large scale.

 

🔓FESTIM is accessible to everyone. FESTIM2 is already usable now and will soon be released as alpha

 

🫵We - the festim developers - want to work with you - potential users - to have it benefit your work.