Advancing Tritium Self-Sufficiency in Fusion Power Plants:

Insights from the BABY Experiment

Remi Delaporte-Mathurin, Nikola Goles, Colin Dunn, Emily Edwards, Samuele Meschini, Stefano Segantin, Sara Ferry, Ethan Peterson, Dennis Whyte, Edward Lamere, Colin Weaver, Kevin Woller and LIBRA collaborators

HWS 2024 conference, Chamonix

\mathrm{n} + ^6\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + 4.8 \ \mathrm{MeV}
\mathrm{n} + ^7\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + \mathrm{n} - 2.5 \ \mathrm{MeV}
\mathrm{TBR} = \mathrm{\frac{tritium \ produced}{tritium \ consumed}} > 1

❓How ❓

Lithium is used to breed tritium

\mathrm{D} + \mathrm{T} \rightarrow \mathrm{He} + \mathrm{n}
\mathrm{n} + ^6\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + 4.8 \ \mathrm{MeV}
\mathrm{n} + ^7\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + \mathrm{n} - 2.5 \ \mathrm{MeV}

The tritium issue

\mathrm{D} + \mathrm{T} \rightarrow \mathrm{He} + \mathrm{n}
1 \ \text{GWth} \approx 10^{20} \ \text{reactions/s} \approx 50\ \text{kg/year}

Cost: $30,000 per gram

Half-life: 12 years

\mathrm{T} \rightarrow \mathrm{He} + \mathrm{e}^-

☢

⚛️Breeding tritium

🛡️Shield from neutrons

🔥Extract heat

Liquid Immersion Blanket

FLiBe

ARC power plant

Sorbom et al, Fus Eng Design, Volume 100, November 2015, Pages 378-405

LIBRA: demonstrating the LIB

What is the smallest blanket that can demonstrate a \(\mathrm{TBR} \geq 1\) ?

LIBRA

Liquid Immersion Blanket tritium Robust Accountancy

Objectives

🎯T self-sufficiency with DT neutrons

🎯Experience with molten salt handling

🎯Tritium extraction from molten salts

Ferry, S. E. et al. (2023), Fusion Science and Technology, 79(1), pp. 13–35. doi: 10.1080/15361055.2022.2078136.

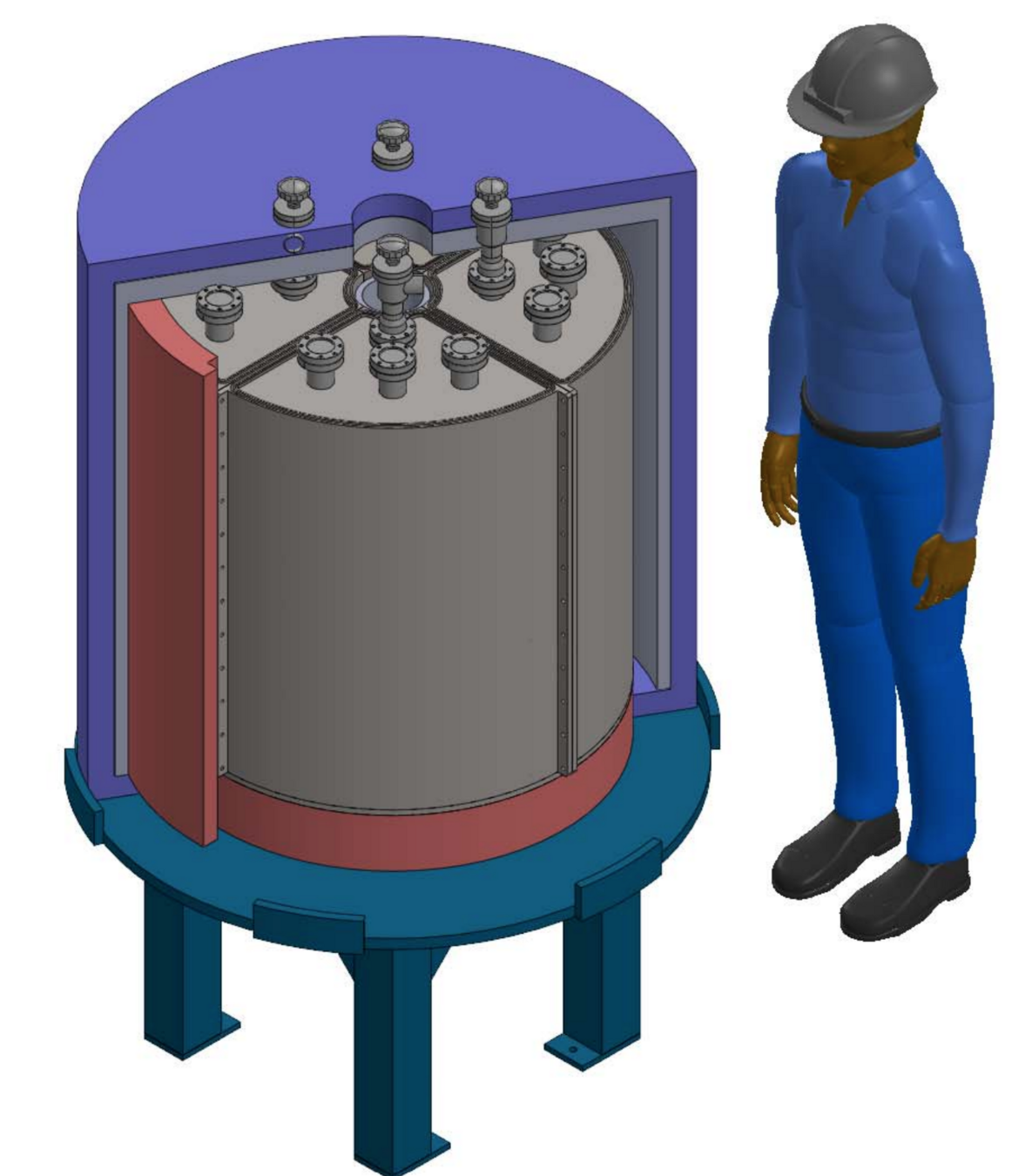
The BABY experiment studies tritium breeding at a small scale

  1. \(14 \ \mathrm{MeV}\) neutrons generated
  2. tritium created from nuclear reactions
  3. tritium transport in the salt
  4. tritium released into the gas phase
  5. tritium collection and accountancy

Molten salt

neutron generator

Tritium collection

reentrant heater

500L FLiBe

14 MeV neutron source

Inconel

double wall

Li + n → T + He

Neutron multiplier

The LIBRA experiment

Tritium transport

Transport mechanisms:

  • Diffusion
  • Advection

Release pathways:

  • Release gas/liquid interface
  • Permeation through walls

The LIBRA experiment

The LIBRA experiment

He

Tritium detection

LIBRA was designed to achieve TBR ≈ 1

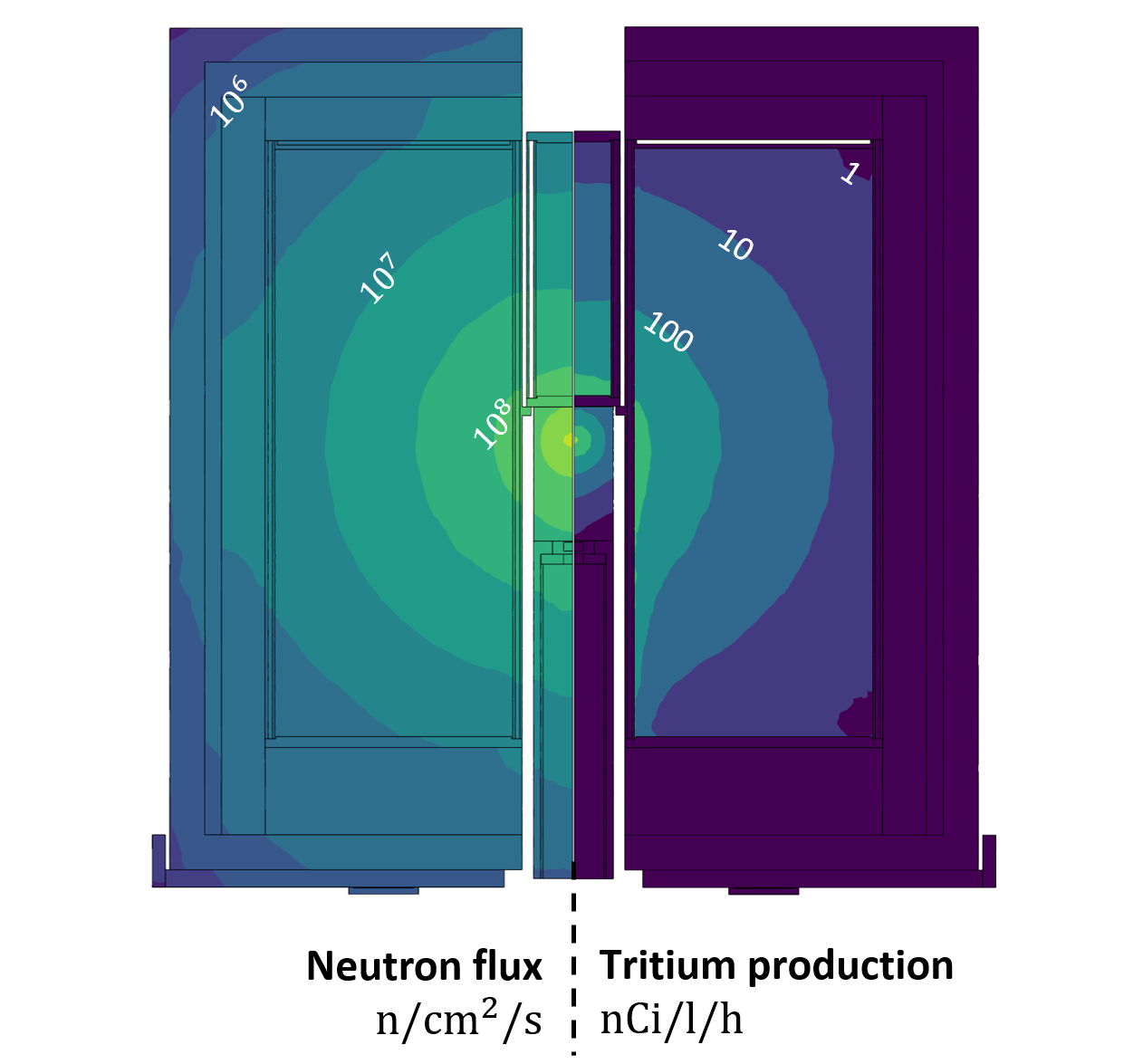
\mathrm{TBR} = \mathrm{\frac{T \ produced}{T \ consumed}}
= \mathrm{\frac{T \ produced}{neutron \ produced}}

Neutronics simulations

Let's start smaller

  • 14 MeV neutron generator \( 10^{10} \) n/s
  • 500 L of FLiBe

→ Never done at MIT ⚠️

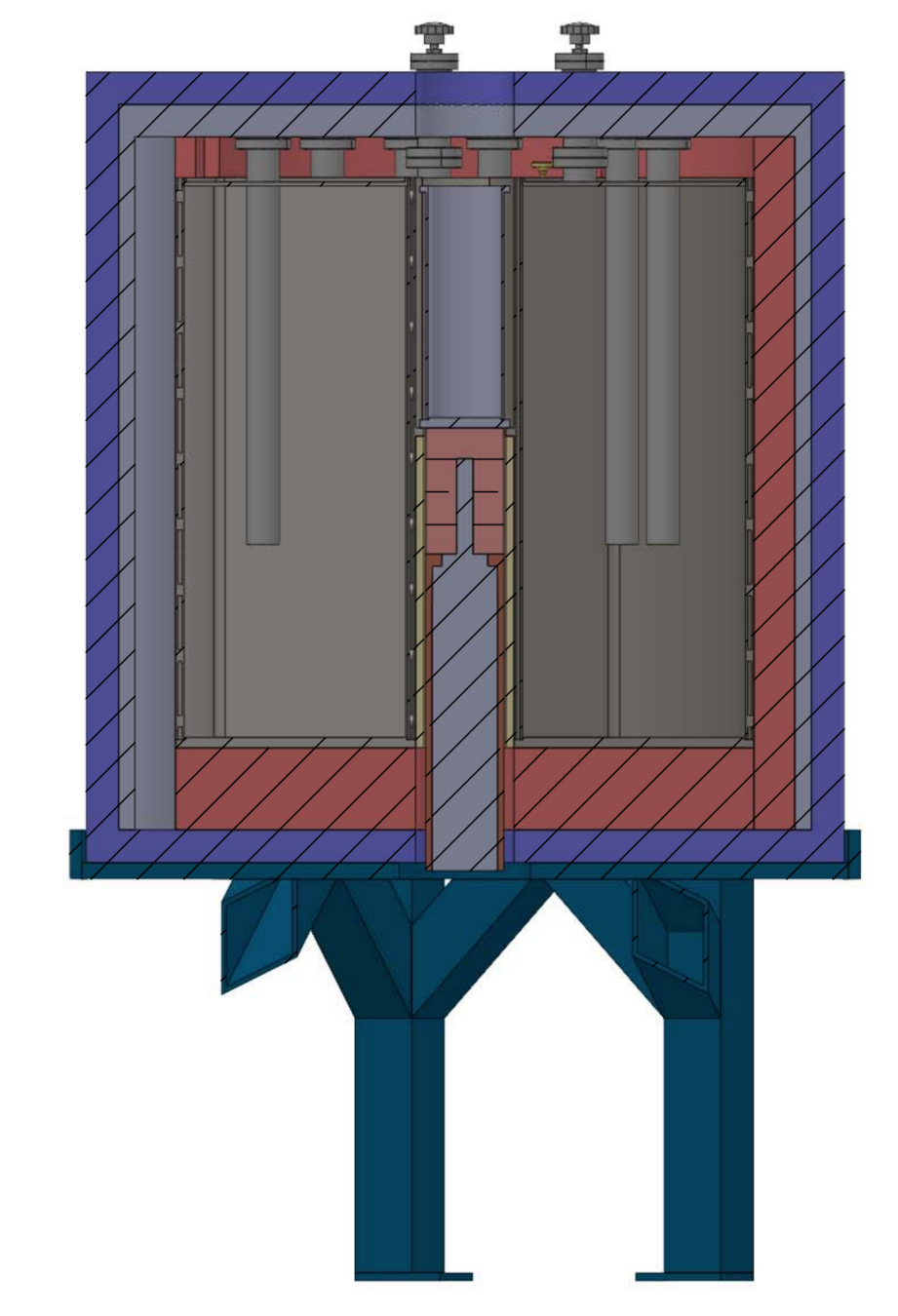
The BABY programme

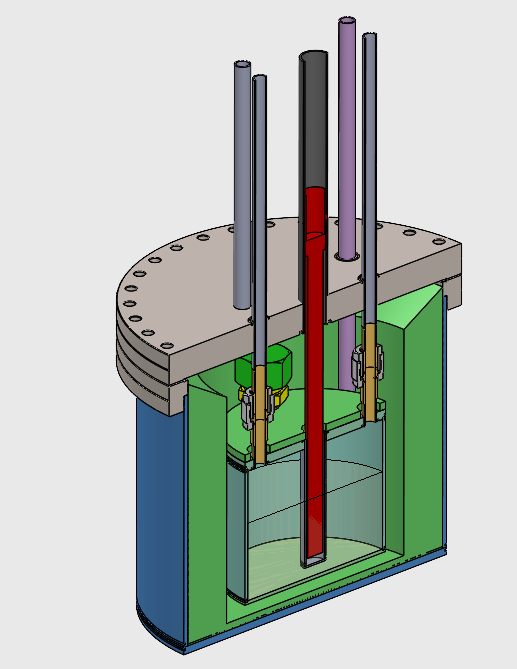
The BABY experiment breeds tritium at a smaller scale

① neutrons are generated

 

② tritium is created from nuclear reactions

 

③ tritium is transported in the salt

 

④ tritium is released into the gas phase

 

⑤ tritium is collected and counted

How to measure TBR?

\mathrm{TBR} = \mathrm{\frac{T \ produced}{T \ consumed}}
= \mathrm{\frac{T \ produced}{n \ produced}}

We need to measure these two numbers!

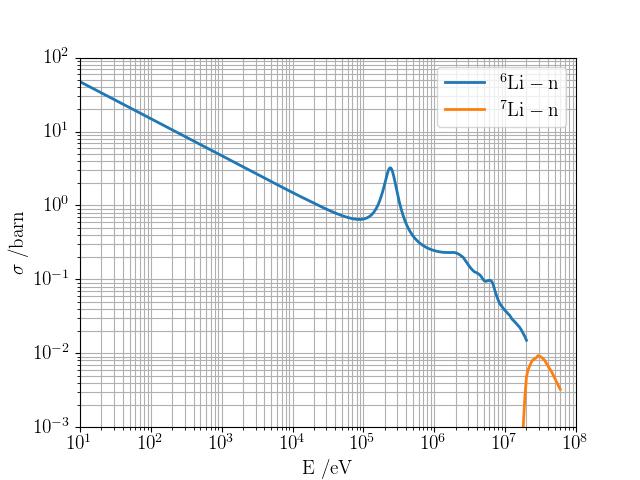
Neutrons are detected with a combination of techniques

3.35\times10^{13}\ \mathrm{n}

Niobium activation foils

Diamond detector

Over 24 h

\( (n,\alpha)\) peak provide information on DT neutron rate

Neutron detection

Tritium was measured with Liquid Scintillation Counting

HTO, TF and TCl

(soluble in water)

HT, T2

(insoluble)

Liquid Scintillation Counting

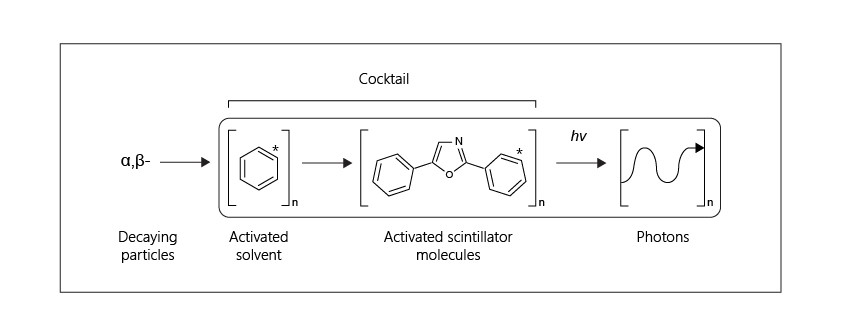
Counts between 0-18.6 keV for tritium detection

21 Bq of tritium have been collected

~100 % of the tritium as HT!

Making the salt more oxidising drives the speciation towards soluble forms

The TBR measurement somewhat  agrees with neutronics simulations 

Where did the tritium go?

\mathrm{TBR} = \frac{1.17\times10^{10} \ \mathrm{T}}{3.35\times10^{13}\ \mathrm{n} }
= {3.57\times10^{-4}}

Modelled TBR (OpenMC)

Measured TBR

OpenMC model

OpenMC model

Comparison of TBR calculations with different breeders

At the 100 mL scale

V \frac{d c_\mathrm{salt}}{dt} = S - \textcolor{#438343}{Q_\mathrm{wall}} - \textcolor{#2a7eb8}{Q_\mathrm{top}}
Q_i = A_i \ k_i \ (c_\mathrm{salt} - c_\mathrm{external}) \\ \approx A_i \ k_i \ c_\mathrm{salt}
S = \mathrm{TBR} \cdot \Gamma_n

A transient 0D model is used to simulate the different releases

\(k\) mass transport coefficient

\(A\) surface area

neutron rate

100 mL salt

Top release

Wall release

  • \( \mathrm{TBR} = 4.71 \times 10^{-4} \) (from OpenMC)
  • \( \Gamma_n = 3.88 \times 10^8 \) n/s (from measurement)
  • Mass transport coeffs. \( k_i \) (fitted)

100 mL

salt

Top release

Wall release

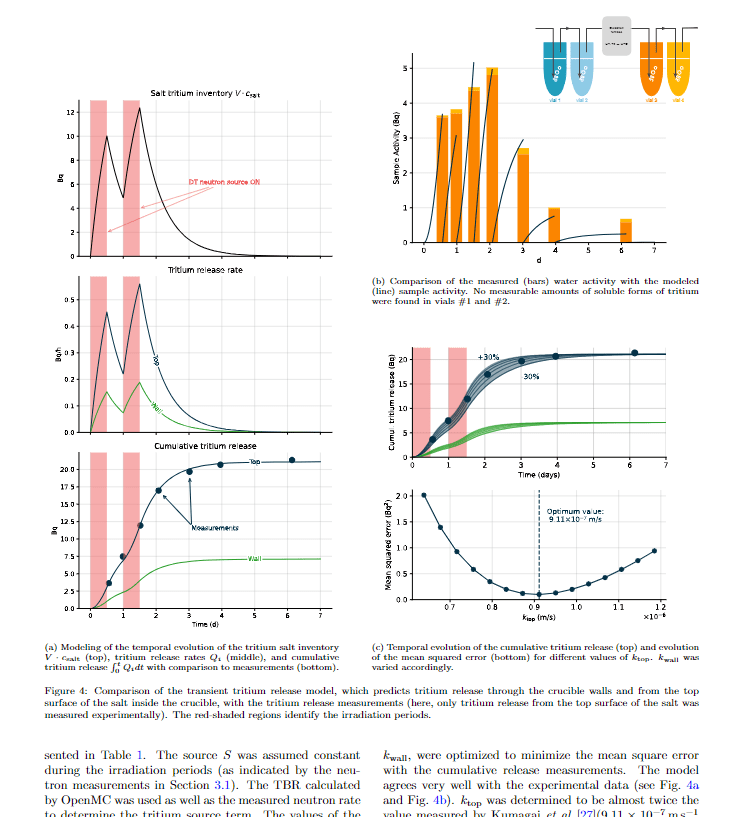
A transient 0D model is used to simulate the different releases

Cumulative release

Neutron generators on

Salt T inventory

T fluxes

Cumulative release

Varying the mass transfer coefficients only affects the dynamics

Reproducibility

Higher fidelity FESTIM¹ model

\frac{\partial c}{\partial t} = \nabla \cdot (D \nabla c) + S + v\cdot \nabla c

¹ Delaporte-Mathurin et al, International Journal of Hydrogen Energy 63, 2024, 786-802

Temperature

(steady state)

Velocity

(steady state)

Tritium concentration

The FESTIM model highlights a qualitative discrepancy 

  • Very sensitive to diffusivity
  • Wall release > Top release

Hypotheses

  • Advection not correctly taken into account?
  • Permeation barrier: oxide layer?
  • Complex chemistry?

Top release

Wall release

\varphi = \int_{\partial \Omega} -D \nabla c \cdot \mathbf{n} \ dS

The flux is computed from the concentration field

\mathrm{cumulative \ release} = A \int_0^t \varphi \ dt

Diffusivities of FLiBe and FLiNaK

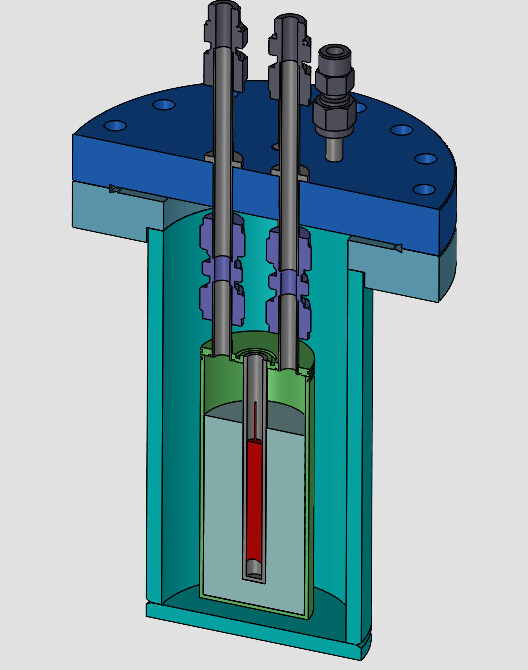
1L of salt

Top release gas sweep

Outer-vessel for capturing permeated tritium

The next design will collect the permeated tritium

Conclusions and next steps

So much more we can do

  • Continue to improve neutron detection and source characterisation
  • Larger volume of salt
  • Collect permeated tritium
  • FLiBe
  • Road to LIBRA and \(\mathrm{TBR} \sim 1 \)

100 mL

1 L

100 L

500 L

BABY

LIBRA

Thank you!

Any question?

remidm@mit.edu