SOFE Short Course
Tritium transport in materials
June 21-22
Remi Delaporte-Mathurin
Agenda
Day 1 – Saturday, 21 June 2025
08:15 – 09:15 General Introduction, tritium in fusion – Remi Delaporte-Mathurin
09:15 – 09:30 Coffee Break
09:30 – 10:30 Modelling hydrogen transport: reactor scale and fuel cycle – Samuele Meschini
10:30 – 11:30 Modelling hydrogen transport: component to reactor scale – Remi Delaporte-Mathurin
11:30 – 12:30 Modelling hydrogen transport: atomistic scale – Stephen Lam
12:30 – 13:30 Lunch
13:30 – 15:30 Experimental techniques and material characterization – Thomas Fuerst, Hans Gietl
15:30 – 15:45 Coffee break
15:45 – 17:00 Q&A
Day 2 – Sunday, 22 June 2025
08:30 – 16:00 FESTIM workshop – Remi Delaporte-Mathurin, James Dark
Round of introductions
Introuction - Dr. Remi Delaporte-Mathurin
- 2022-today: Researcher at the Plasma Science and Fusion Center, MIT
-
2018-2019: Ph.D. French Atomic Energy Authority (CEA Cadarache) and University Sorbonne Paris Nord
-
2017: CEA Cadarache, IRFM, apprentice
- 2016: UK Atomic Energy Authority
- 2012-2018: M.Sc. Thermal Engineering and Energy Sciences

Joint European Torus (JET), Culham, UK
Introuction - Dr. Remi Delaporte-Mathurin

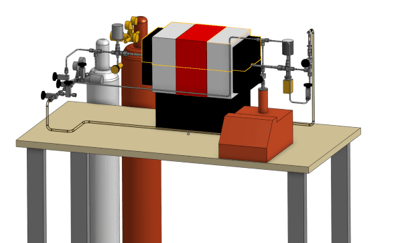
LIBRA tritium breeding experiment
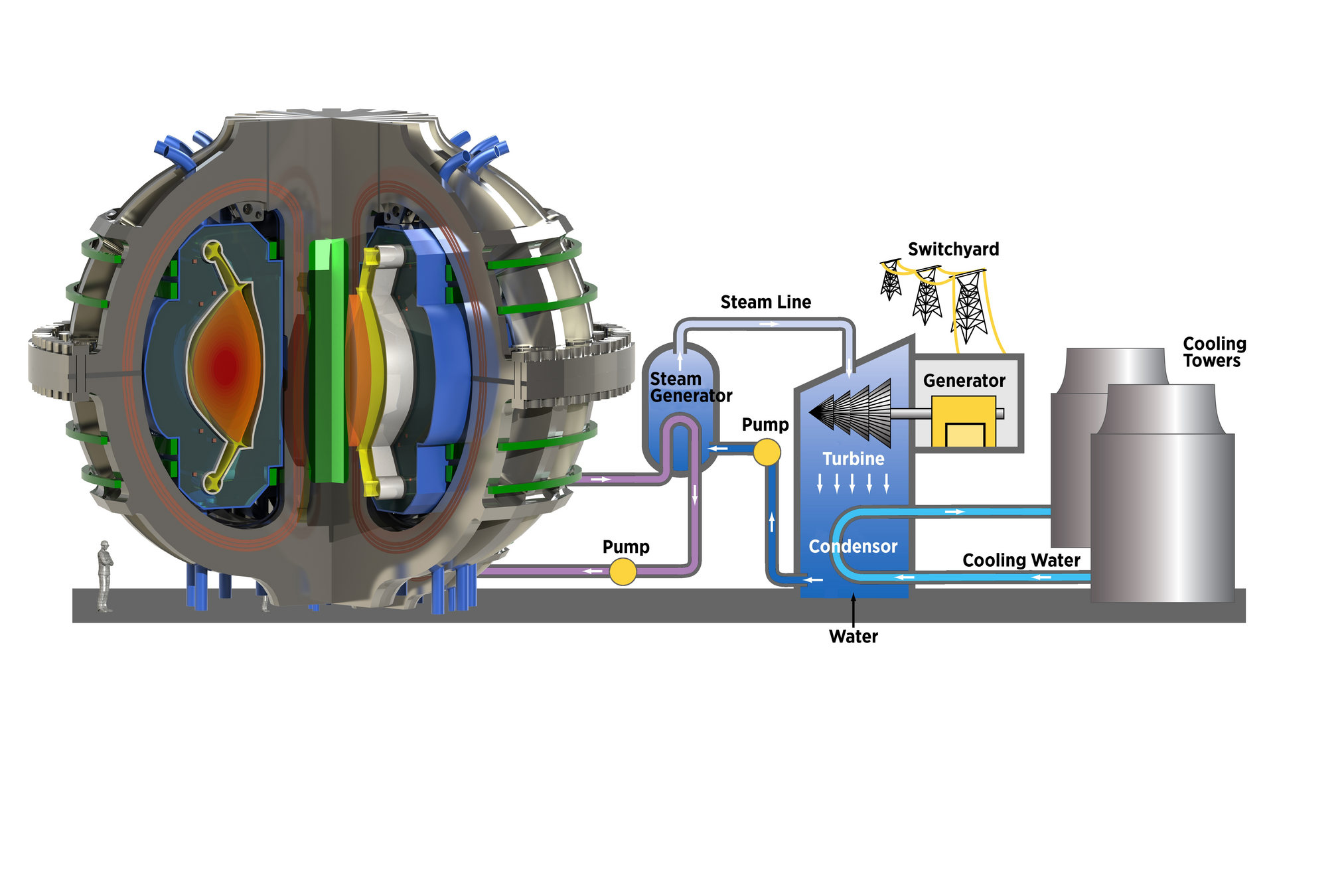
Tritium contamination in a heat exchanger with FESTIM
Hydrogen gas-driven permeation experiment
General Introduction:
tritium in fusion

ITER



Plasma: mixture of Hydrogen (D-T) and Helium
Particle bombardment
Divertor



Why should we care?
T is rare
T is expensive
€£$
Material embrittlement
T is radioactive
☢
What's Tritium?
+
+
+
Protium
Deuterium
Tritium
Molar mass: 6.032 g/mol
What's Tritium?
+
Tritium
☢
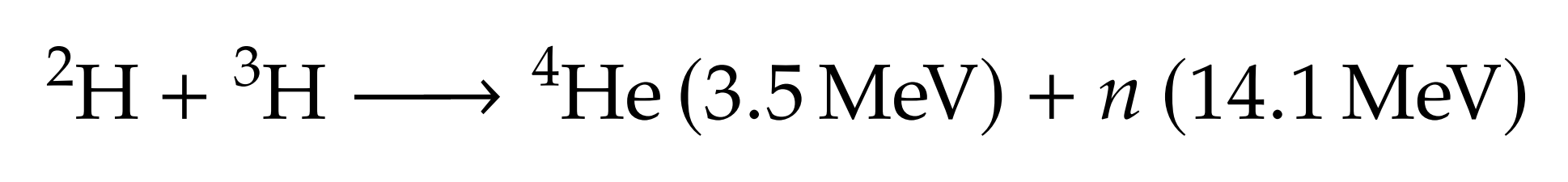
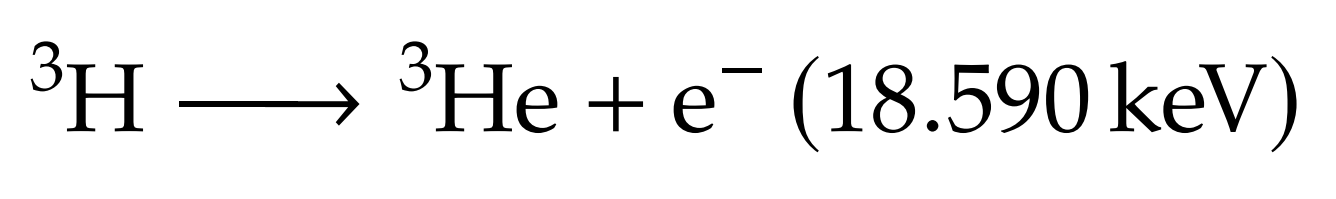
Fuel self-sufficiency

Half-life: 12 years
☢
Consumption of a 1 GWth fusion reactor (1 year)
50 kg
Cost: $30,000 per gram
The breeding blanket

Lithium is used to breed tritium
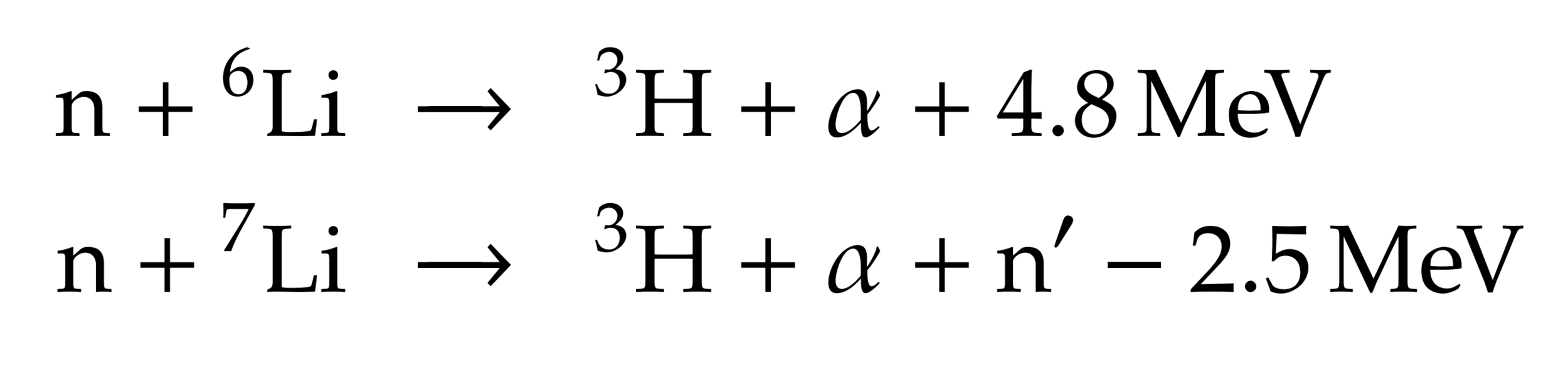
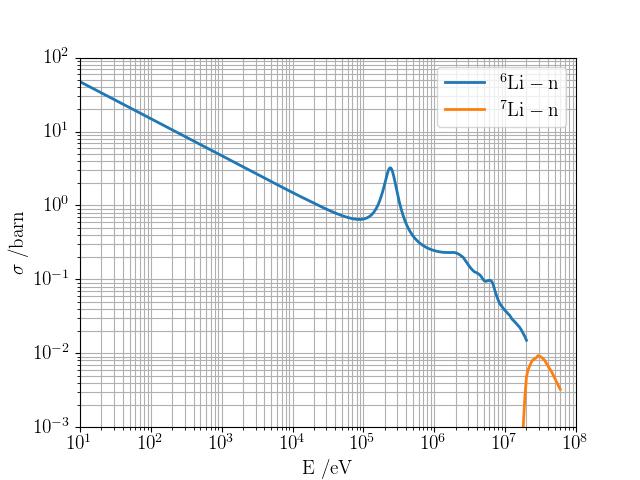
→ Li6 enrichment is an option
DT fusion neutrons

Magnet
Breeding blanket
The breeding blanket
Plasma
The breeding blanket is only one component of the fuel cycle
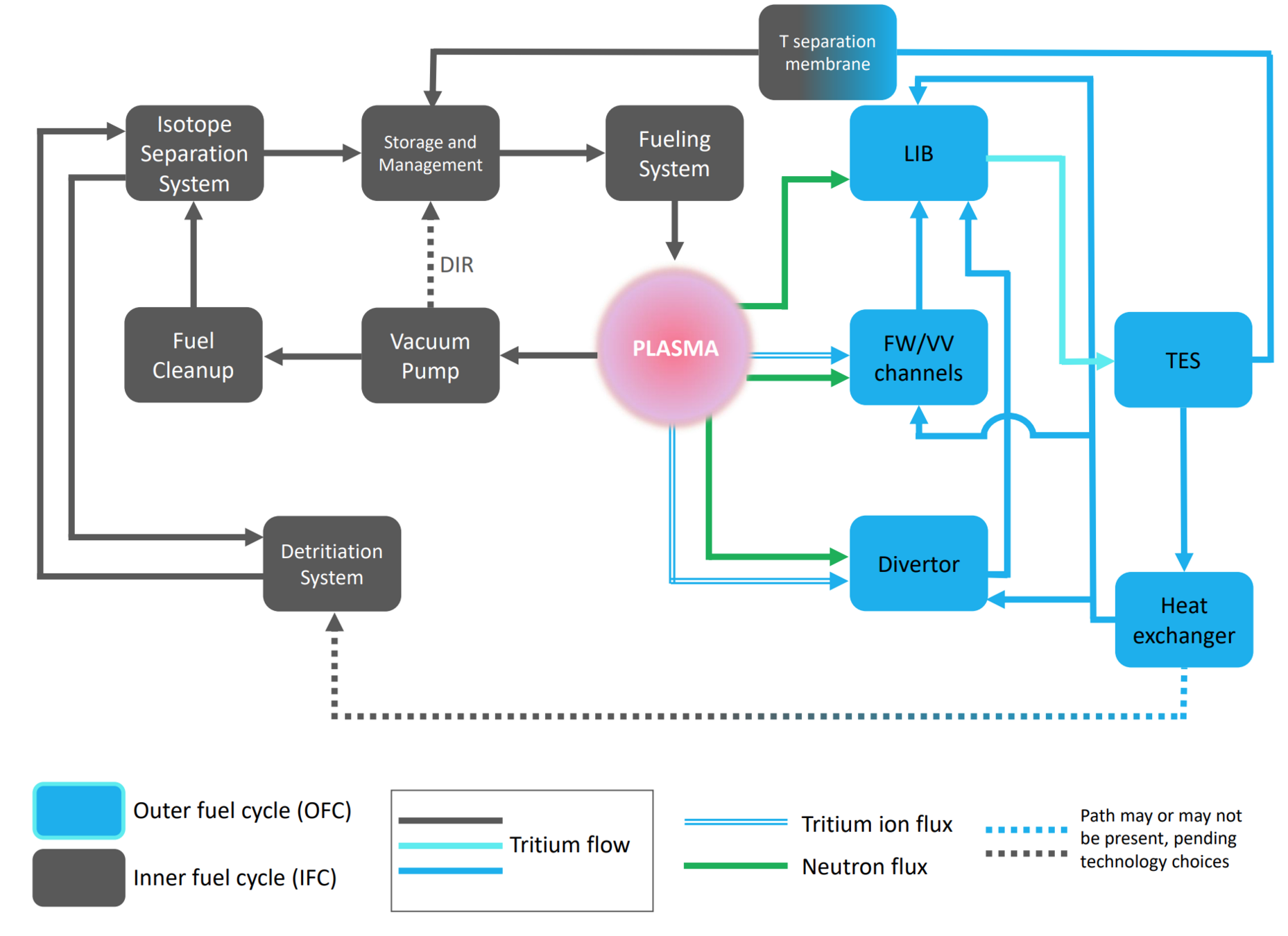
Let's play with a simple fuel cycle model
Burns tritium
Breeds tritium (TBR)
Tritium Extraction System
Breeding Blanket
Plasma
Storage
neutrons
TBR
(constrained by technology)
Doubling time
(driven by economics)
Startup inventory
(constrained by safety)
Startup inventory
Tritium Extraction System
Breeding Blanket
Plasma
Storage
Safety issues
Tritium is a health hazard
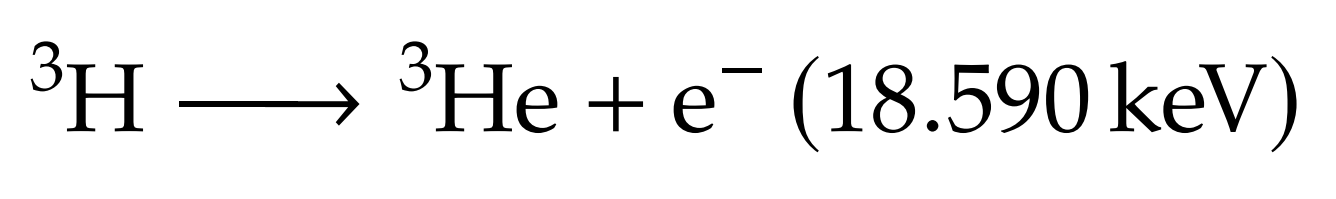
☢
- No external hazard: electron stopped by skin
- Once ingested, can cause damage to internal tissues
- Forms: HT, HTO, methane, titrides...
- Biological half-life of HTO: 10 days
- Biological half-life of OBT (Organically Bound Tritium): 40 days
Augustin Janssens. ‘Emerging Issues on Tritium and Low Energy Beta Emitters”’. en. In: (Nov. 2007), p. 100
| Country | Water limit (Bq/L) |
|---|---|
| EU | 100 |
| USA | 740 |
| UK | 100 |
| Canada | 7,000 |
| Finland | 30,000 |
| Australia | 76,103 |
| Russia | 7,700 |
| WHO | 10,000 |


Tritium US DOE Handbook
413 pages!
The tritium content needs to be limited
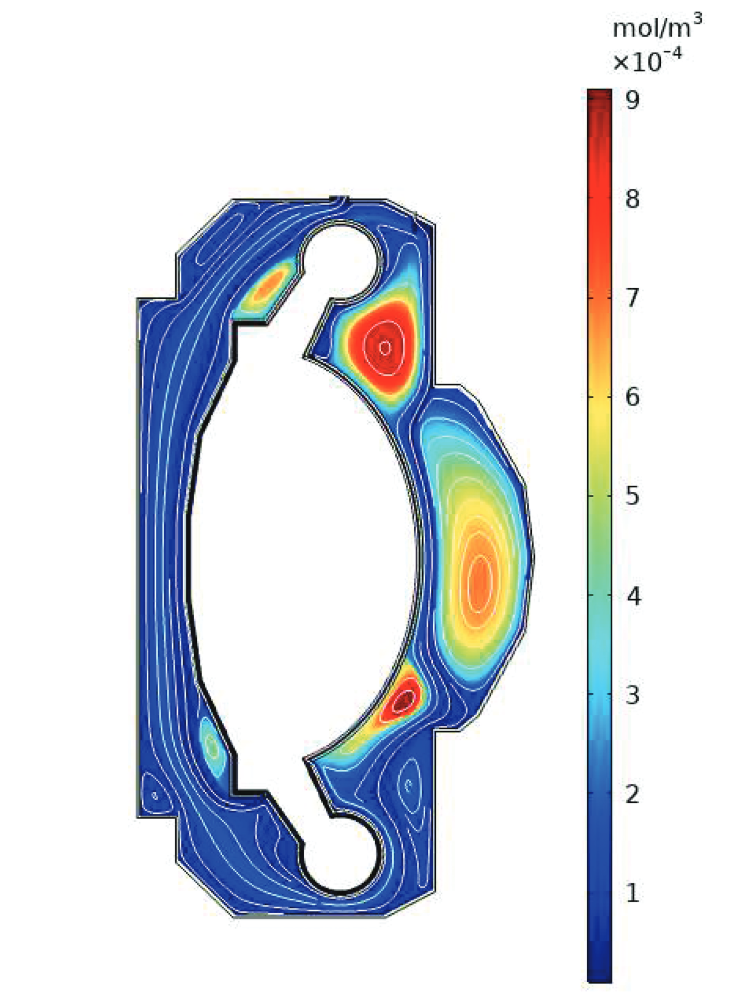
1. Keep inventory at a minimum
Tritium limit in the ITER vacuum vessel: 1 kg
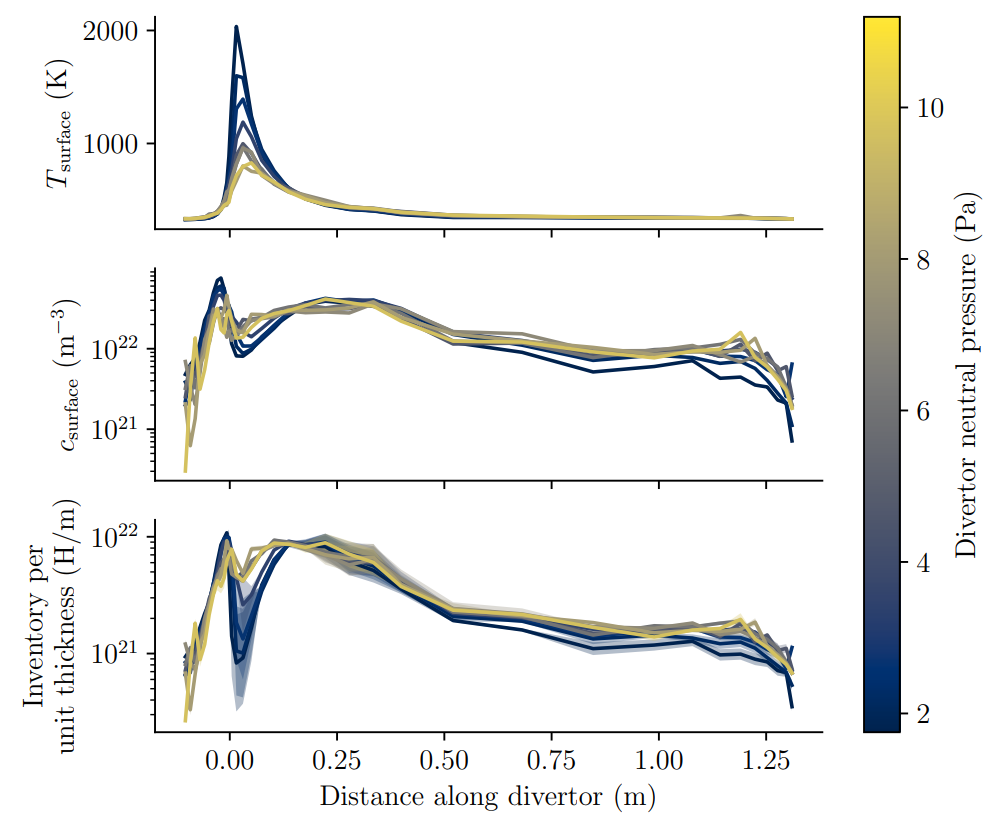
1. Keep inventory at a minimum
2. Reduce inventory
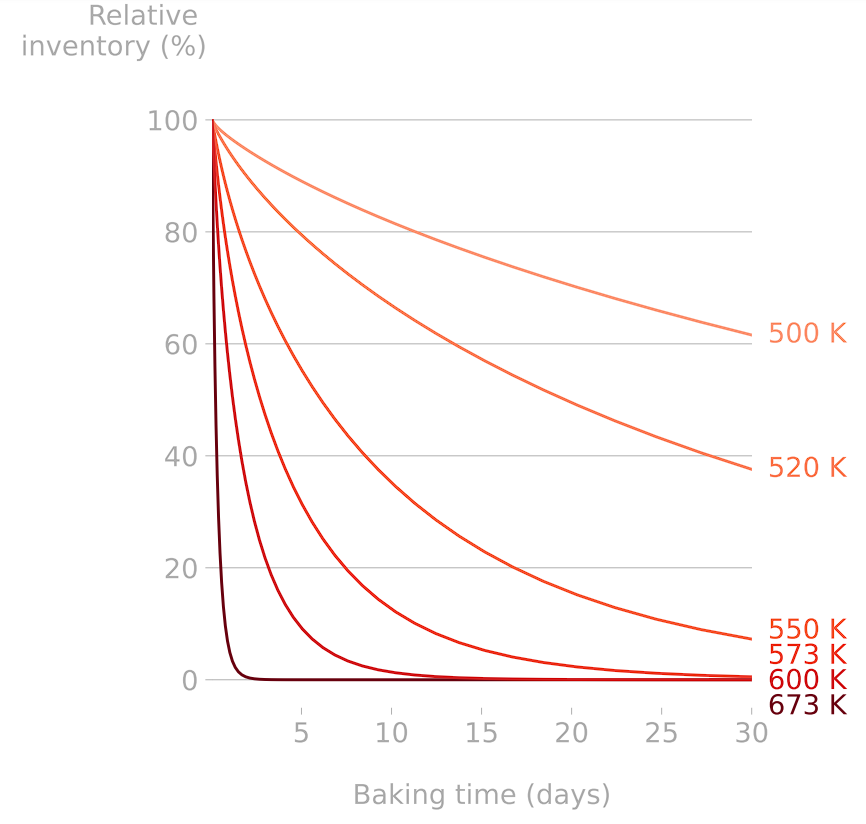
Heating components help releasing their tritium content (cf. Basics of H transport)

The tritium content needs to be limited
1. Keep inventory at a minimum
2. Reduce inventory
3. Avoid contamination of coolants
Metal
Tritiated environment
"Clean" environment
Permeation
The tritium content needs to be limited
1. Keep inventory at a minimum
2. Reduce inventory
3. Avoid contamination of coolants
Metal
Tritiated environment
"Clean" environment
Permeation barrier
Permeation
The tritium content needs to be limited
1. Keep inventory at a minimum
2. Reduce inventory
3. Avoid contamination of coolants
Ceramics are promising candidates:
- oxides
- carbides
- nitrides
Permeation barriers are caracterised by their PRF (Permeation Reduction Factor)
Target for breeding blankets PRF ≈ 100-1000
Luo et al Surface and Coatings Technology 2020
The tritium content needs to be limited
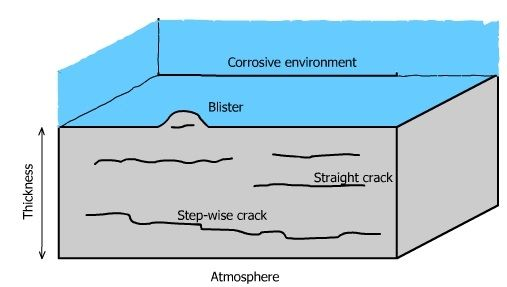
Component embrittlement
Agglomeration of hydrogen can lead to blistering

- Accumulation of H at defects:
- Voids
- Reaction with impurities (formation of methane)
- grain boundaries
- Creation of a filled cavity
- Growth of the cavity without bursting
Kuznetsov, Alexey S. et al. “Hydrogen-induced blistering of Mo/Si multilayers: Uptake and distribution.” Thin Solid Films 545 (2013): 571-579.
Cavities can lead to Hydrogen Induced Cracking
Review of HIC by Sofronis
https://doi.org/10.1016/j.jngse.2022.104547

Take aways
H transport
Safety
Fusion Economy
Materials
- Minimising inventories
- Limiting permeation
- Protecting personel
- Fuel cycle
- Tritium breeding
- Losses
- Embrittlement
- H induced cracks
DFT
Multi-scale hydrogen transport
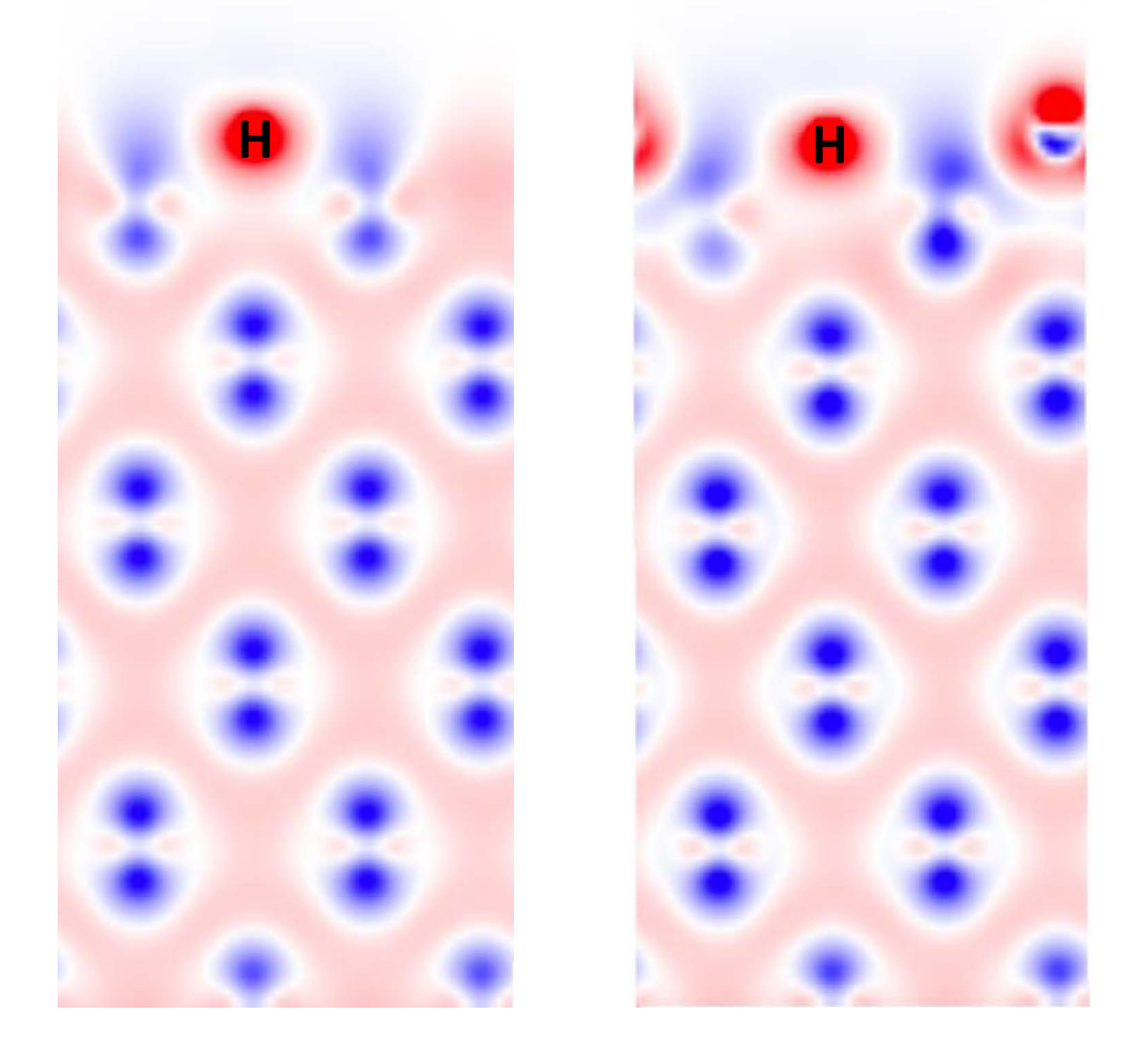
Y. Ferro et al 2023 Nucl. Fusion 63 036017
Length scale
Time scale
MD
Length scale
Time scale
DFT

potentials
Multi-scale hydrogen transport
Component scale modelling

Length scale
Time scale
MD
DFT


D, S, other coeffs.
Multi-scale hydrogen transport
Length scale
Time scale
MD
DFT


Component scale modelling


Fuel cycle modelling
Residency times, fluxes, ...
Multi-scale hydrogen transport
Length scale
Time scale
MD
DFT


Component scale modelling


Fuel cycle modelling

Abstraction
Multi-scale hydrogen transport
Question time!
Tritium transport theory

Hydrogen transport in metals

Diffusion
Even more particles
continuity approximation
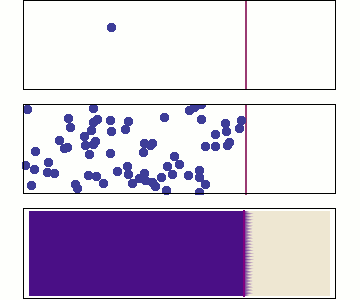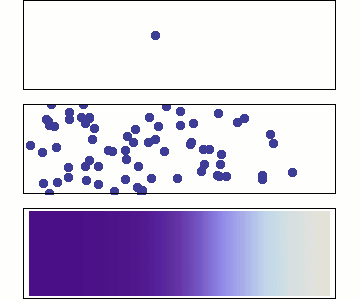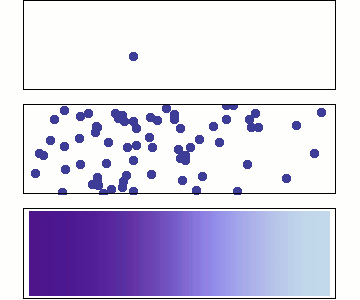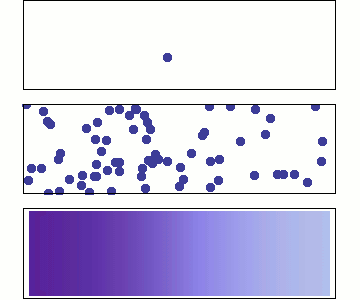
Single particle
Random walk
Many particles
Diffusion
\( \varphi \): diffusion flux
\( D \): diffusion coefficient
\( c \): mobile hydrogen concentration
Fick's 1st law of diffusion
Diffusion
\( \varphi\): diffusion flux
\( D \): diffusion coefficient
\( c \): mobile hydrogen concentration
\( S\): source term
Fick's 1st law of diffusion
Fick's 2nd law of diffusion
Diffusion
\( \varphi\): diffusion flux
\( D \): diffusion coefficient
\( c \): mobile hydrogen concentration
\( S\): source term
Soret effect (or thermophoresis)
Stress assisted diffusion
Particle implantation
Ziegler et al. 2010. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 268 (11): 1818–23. https://doi.org/10.1016/j.nimb.2010.02.091.
Implantation range
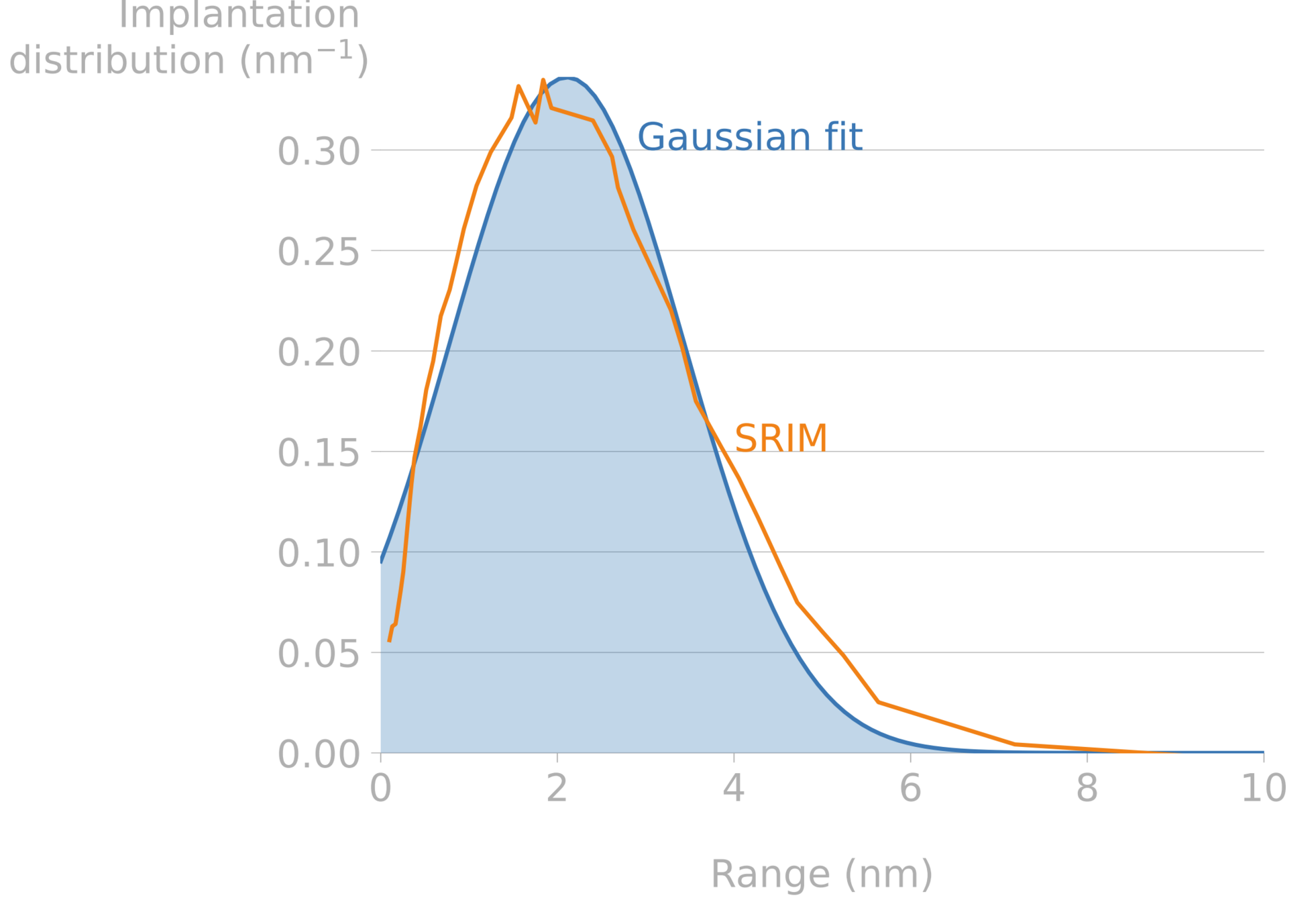
Implantation range & width and reflection coefficient can be computed with SRIM, SDTRIM...
Mutzke et al, SDTrimSP Version 6.00 2019
Particle implantation
\(\Gamma_\mathrm{incident} \): incident flux (particle/m2/s)
\( f(x) \): Gaussian distribution (/m)
\(r \): reflection coefficient
Surface effects
H2 molecules
Metal lattice
Surface effects
Dissociation coefficient (H/m2/s/Pa)
Partial pressure of H (Pa)
Adsorbed H
Metal lattice
Surface effects
Metal lattice
Recombination coefficient (m4/s)
Concentration (H/m3)
Surface effects
Metal lattice
Waelbroeck model
Surface effects
Metal lattice
At equilibrium:
Sievert's law of solubility
Surface effects
Non-metallic liquid
At equilibrium:
Henry's law of solubility
Interfaces
Material 1
Material 2
Interfaces
Partial pressure and flux are continuous
Material 1
Material 2
Interfaces
Material 1
Material 2
Case 1:
Metal-Metal
Sievert's law
Interfaces
Material 1
Material 2
Case 2:
Non metal-non metal
Henry's law
Interfaces
Material 1
Material 2
Case 3:
Metal-Non metal
Sievert's law
Henry's law
Interfaces
Material 1
Material 2
Steady state concentration profile
- different diffusivities \(\rightarrow\) different concentration gradients
- different solubilities \( \rightarrow \) concentration discontinuity
\(x\)
\(c\)
⚠️Very little experimental validation data for interfaces
Permeation barriers are low solubility, low duffisivity
Metal
Tritiated environment
"Clean" environment
Permeation
Permeation barrier
Permeation barriers are low solubility, low duffisivity
Pressure \(P\)
High gradient = high flux
Low gradient = low flux
Pressure \(P\)
Trapping
H
Trap = anything binding to H
- vacancy
- grain boundary
- impurity
- chemical reaction
- ...
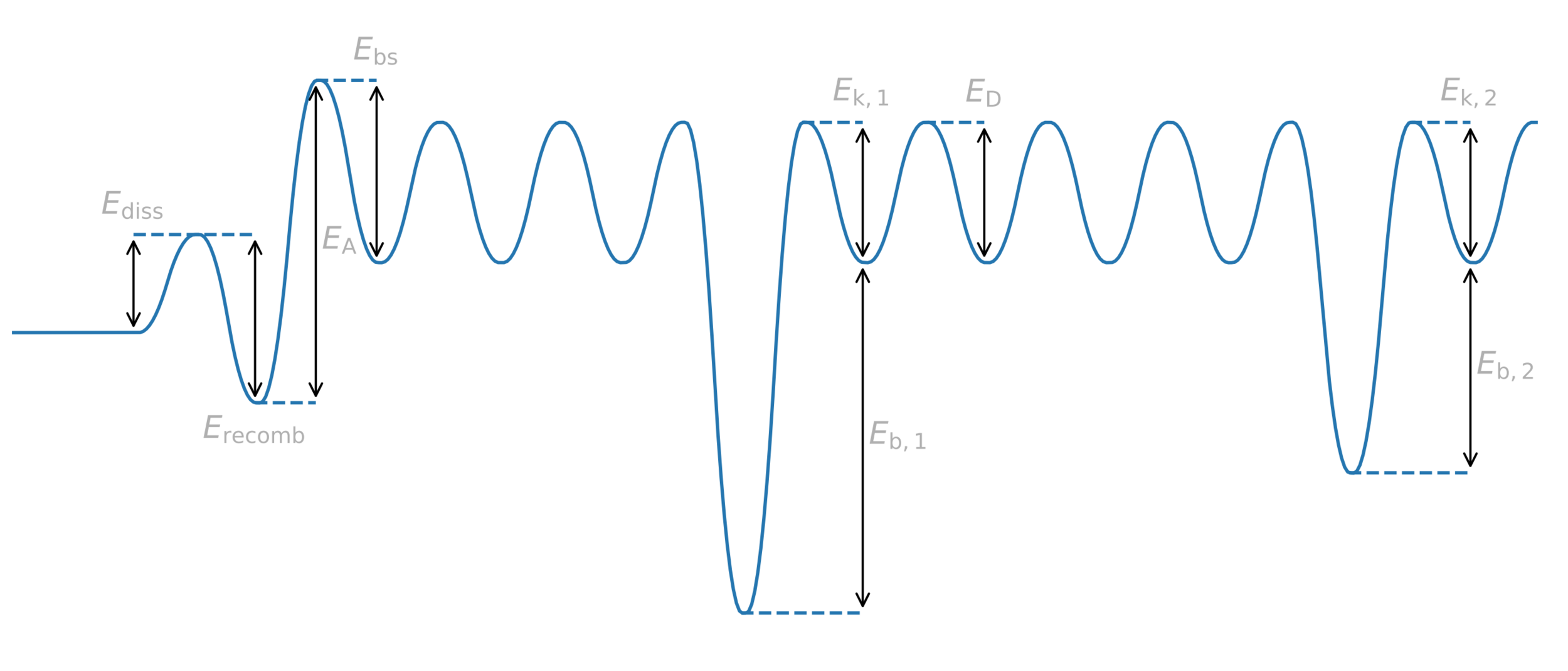
Trapping

H
Potential energy
Distance
Diffusion barrier
Energy barrier = activation energy
Trap binding energy
Trapping energy
Common assumption:
\( E_k = E_D \)
Trapping
0D
Since \(n_\mathrm{trap} = n_\mathrm{free \ trap} + c_\mathrm{t} \)
Trapping
0D
Total concentration of traps
Trapping
0D
With diffusion
and
1 trap
Trapping
N traps
McNabb & Foster model
Trapping
Other models assume traps can hold more than one H
Many of these processes are thermally activated

Recombination
Dissociation
Absorption
Trapping
Detrapping
Diffusion
Arrhenius law
Pre-exponential factor
Activation energy (eV/H)
Temperature (K)
Boltzmann constant (eV/H/K)
Arrhenius law
Pre-exponential factor
Activation energy (J/mol)
Temperature (K)
Gas constant (J/mol/K)
Conversion:
Arrhenius law
\( 1/T \) (1/K)
Arrhenius law
Intercept
+ Slope
Y =
X
Arrhenius law
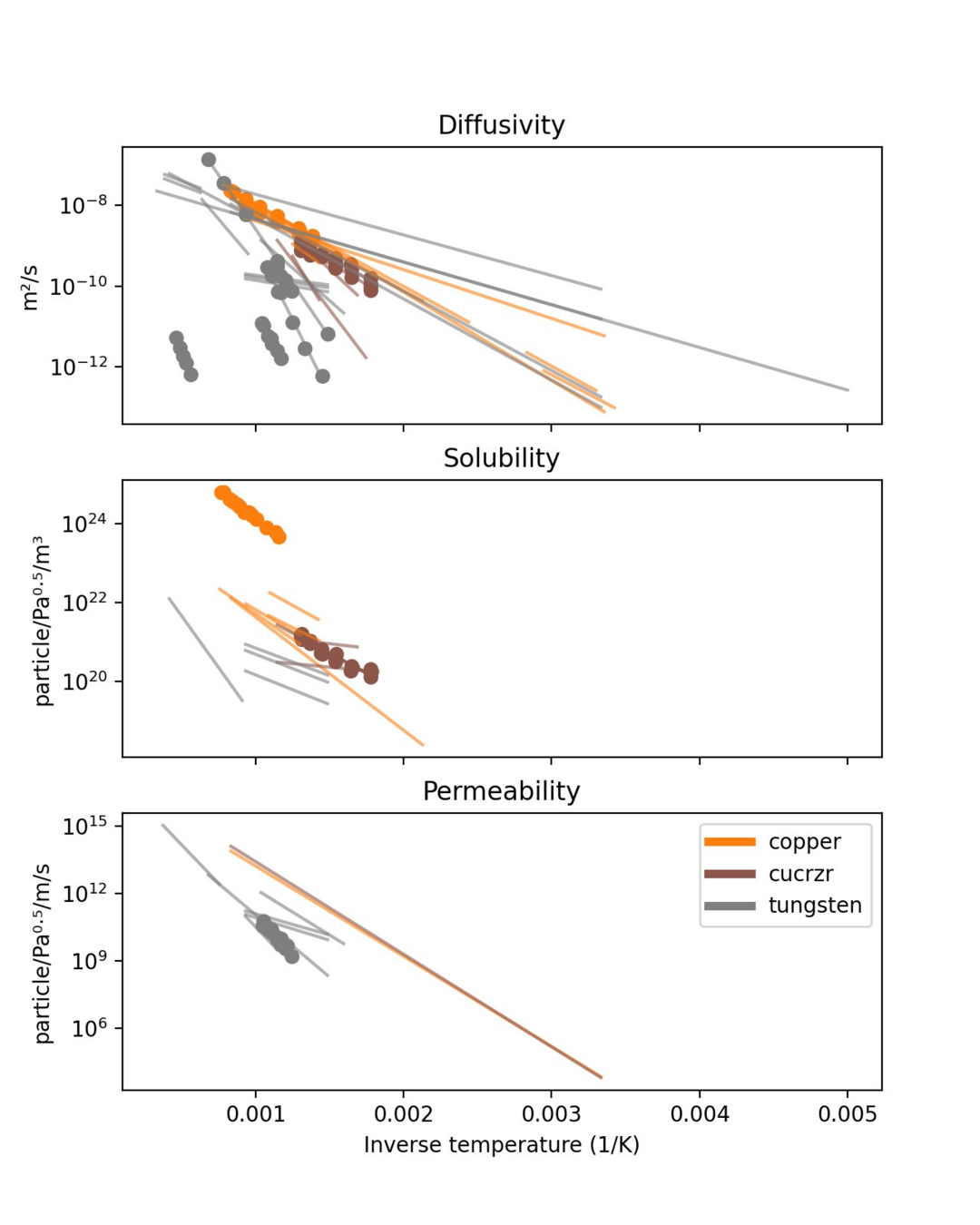
Arrhenius parameters:
- Diffusivity
- Solubility
- Permeability
- Recombination coeff.
- Dissociation coeff.
- Trapping rate
- Detrapping rate
Component scale modelling

McNabb & Foster model
Challenges
- Number of degrees of freedom
- Interface discontinuities
Governing equations
Let's solve the system analytically
Let's solve the system analytically
Simplification #1: 1D domain \(L\)
Let's solve the system analytically
Simplification #1: 1D domain \(L\)
Simplification #2: 1 material
Let's solve the system analytically
Simplification #1: 1D domain \(L=1\)
Simplification #2: 1 material
Simplification #3:
Let's solve the system analytically
Simplification #1: 1D domain \(L\)
Simplification #2: 1 material
Simplification #3:
Simplification #4: Steady state
💡Tip
At steady state, the mobile concentration is independent of trapping
Let's solve the system analytically
Oriani's model
Let's solve the system analytically
2 unknowns =
2 equations =
2 boundary conditions
Let's solve the system analytically
Let's solve the system analytically
Let's solve the system analytically

- Steady state
- 1 material
- Homogeneous temperature
- 1D

We can solve it numerically
Component modelling
Experimental analysis
3 main numerical methods
Finite Difference Method (FDM)
Finite Element Method (FEM)
Finite Volume Method (FVM)
Let's not bother

There are a handful of H transport codes
TMAP7
TMAP8
MHIMS
FESTIM
COMSOL
Abaqus
There are a handful of H transport codes
TMAP7
TMAP8
MHIMS
FESTIM
COMSOL
Abaqus
1D
1D/2D/3D
TESSIM
There are a handful of H transport codes
TMAP7
MHIMS
FDM
FEM
TESSIM
TMAP8
FESTIM
COMSOL
Abaqus
There are a handful of H transport codes
TMAP7
TMAP8
MHIMS
FESTIM
COMSOL
Abaqus
Proprietary
Open-source
Closed-source
TESSIM

COMSOL
- ARC's breeding blanket
- Source of tritium from neutronics calculations
- Heat transfer + Fluid dynamics + H transport
- Steady state
- Computation time 8h
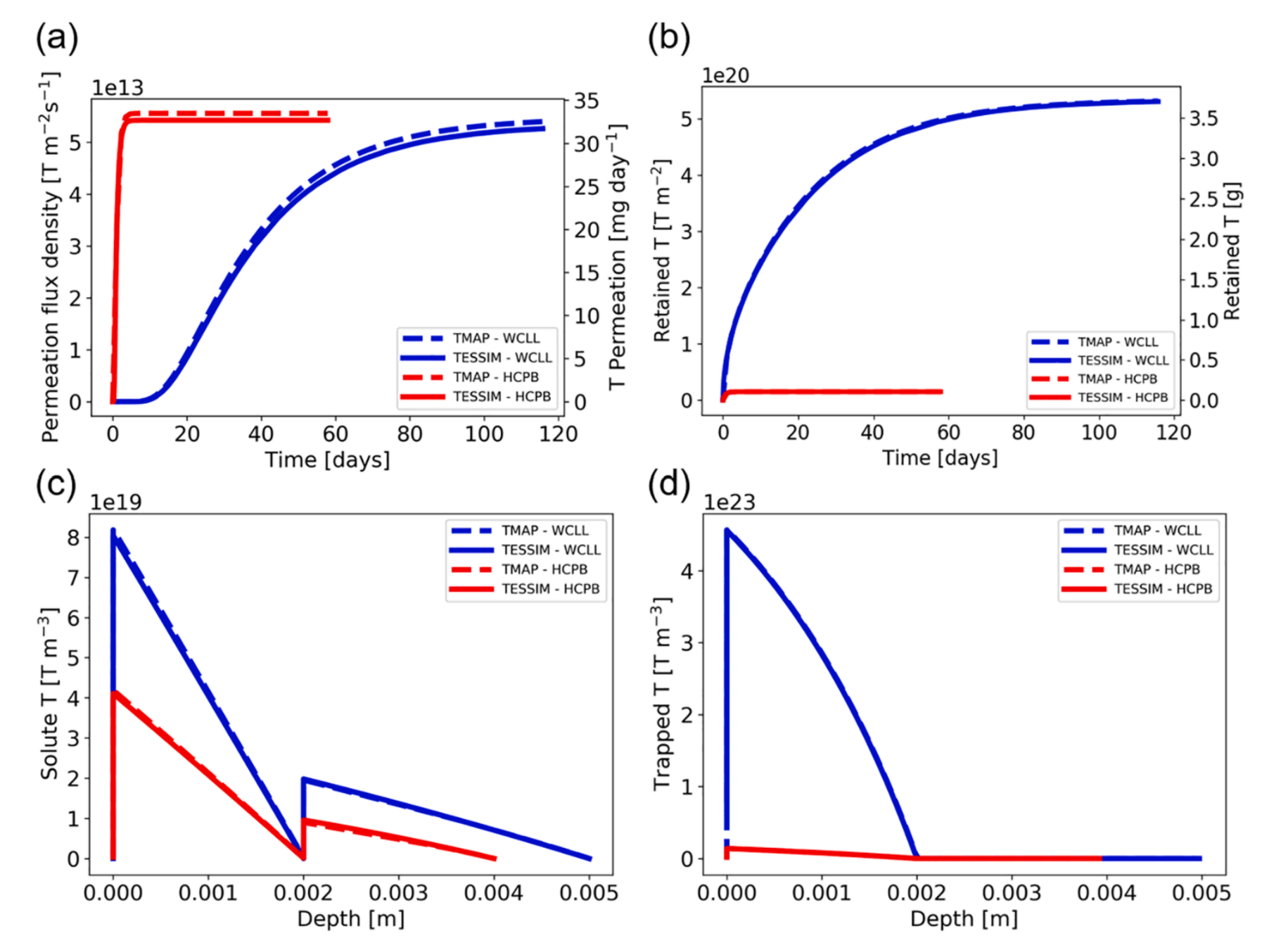
TMAP7 and TESSIM
- W on Eurofer
- 1D
- Agreement between TMAP and TESSIM

How to handle large models
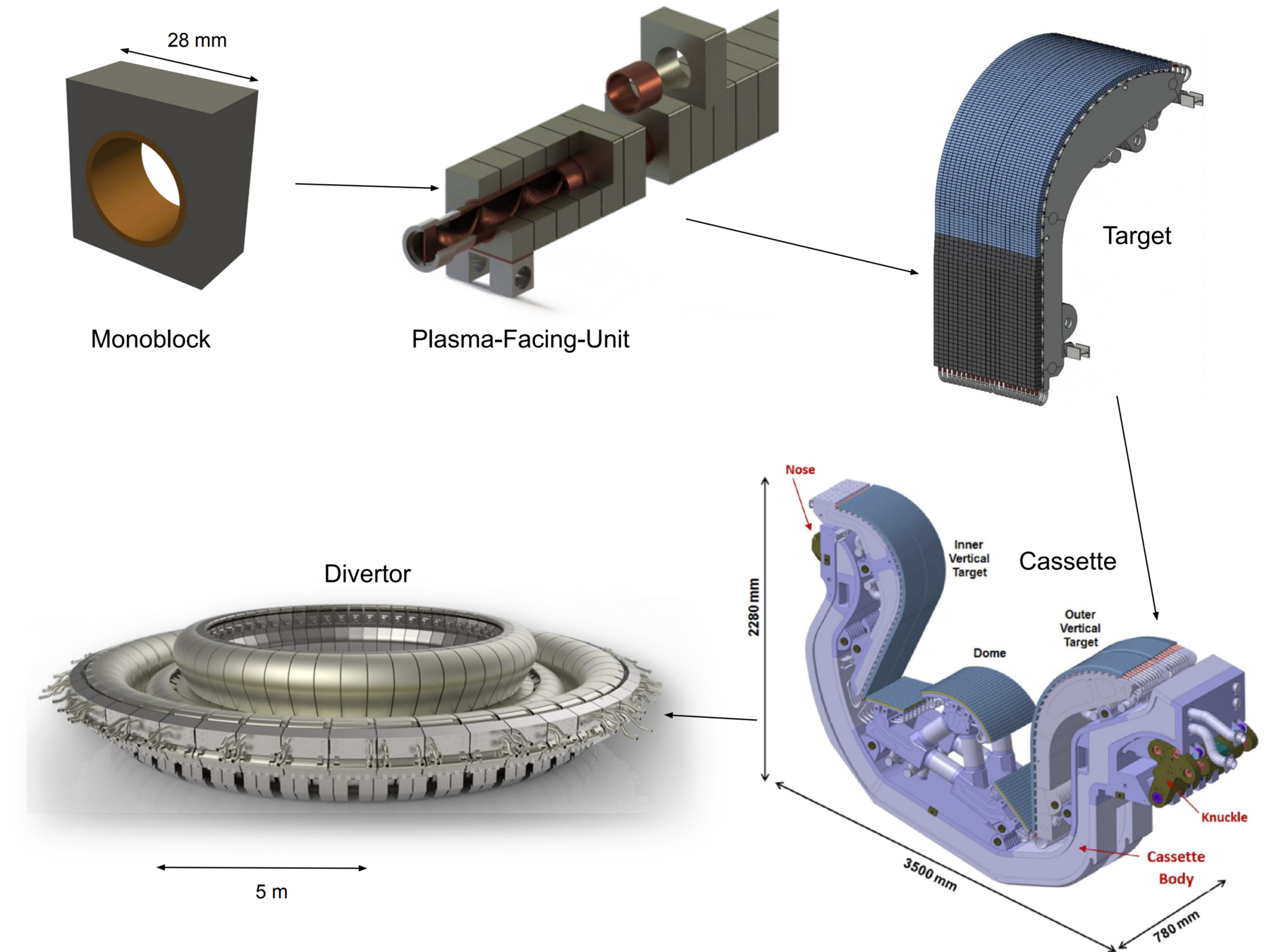
x 10,000
💡Build a surrogate model!
What is the inventory of the whole divertor?
Large problem
A monoblock surrogate model
At
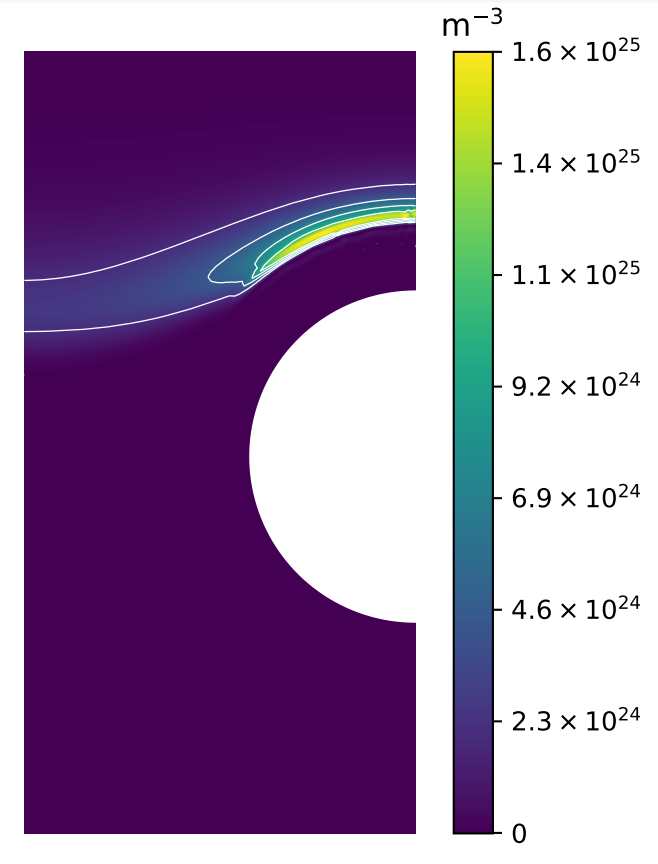

A monoblock surrogate model


+
+
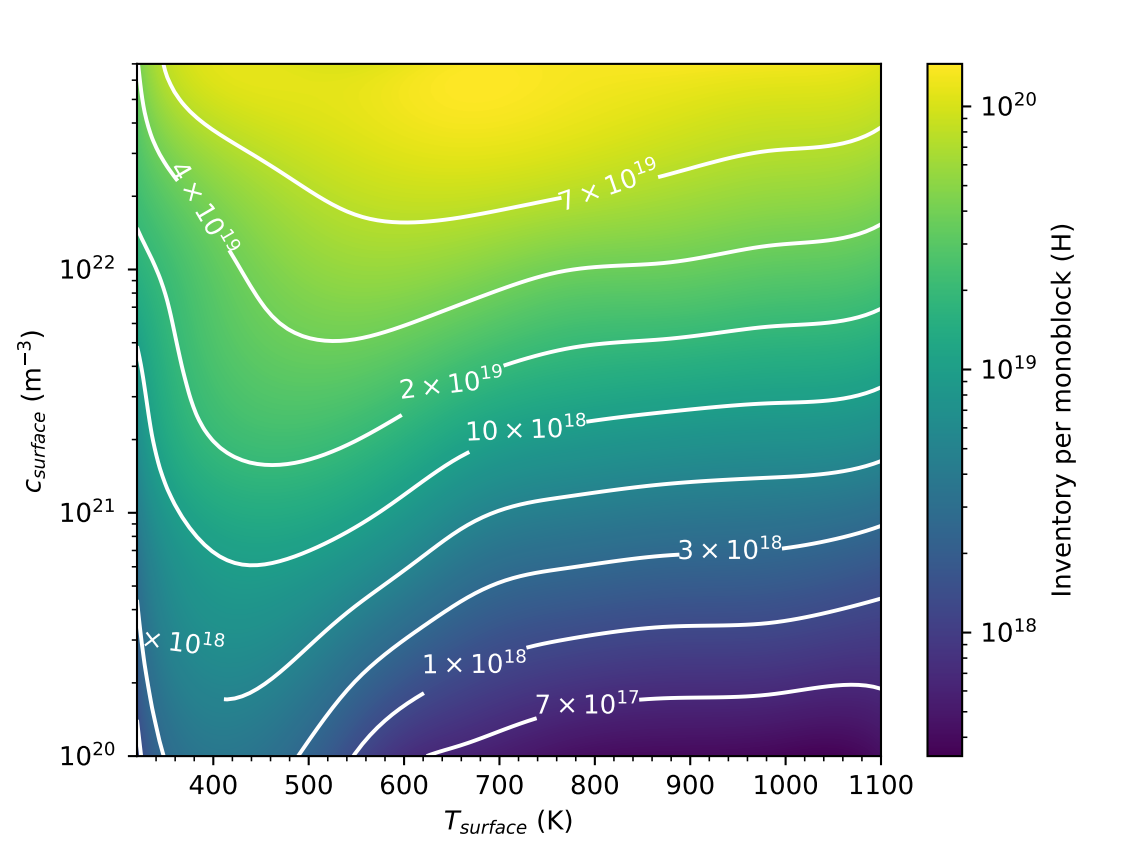
A monoblock surrogate model
+
+

+
+
+
+
+
+
+
+
+
+
+
+
A monoblock surrogate model

At
Gaussian Process Regression (GPR)

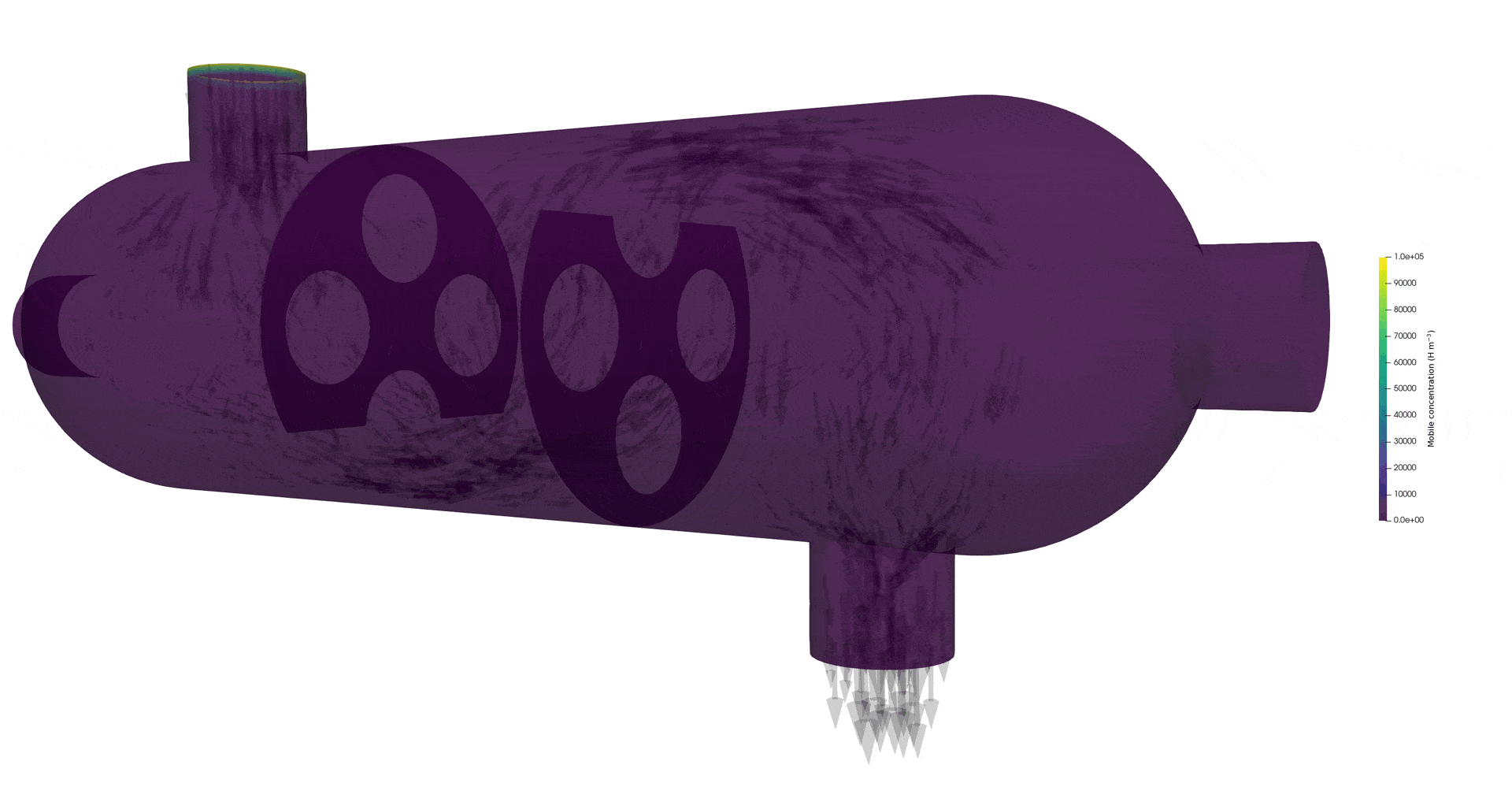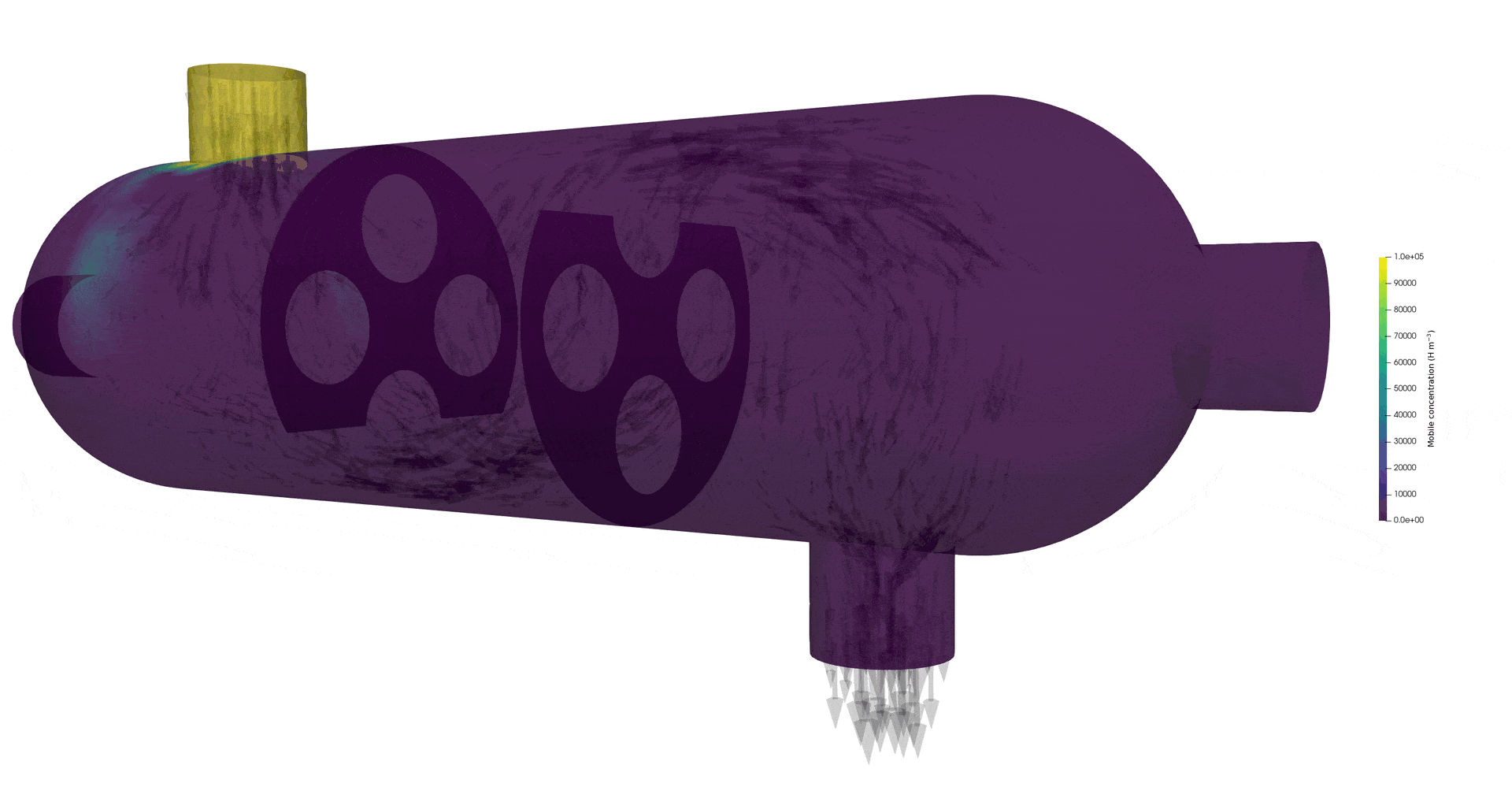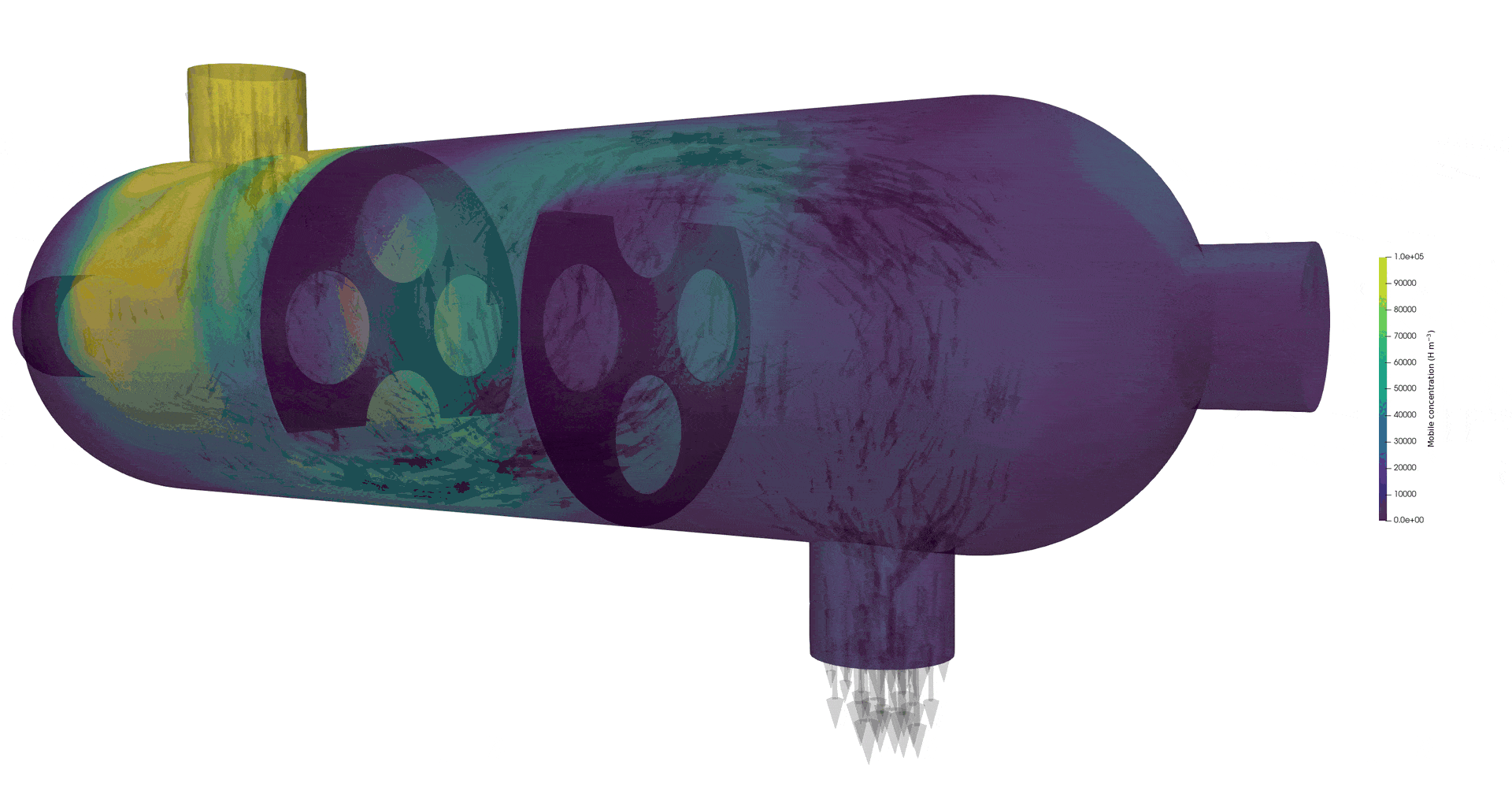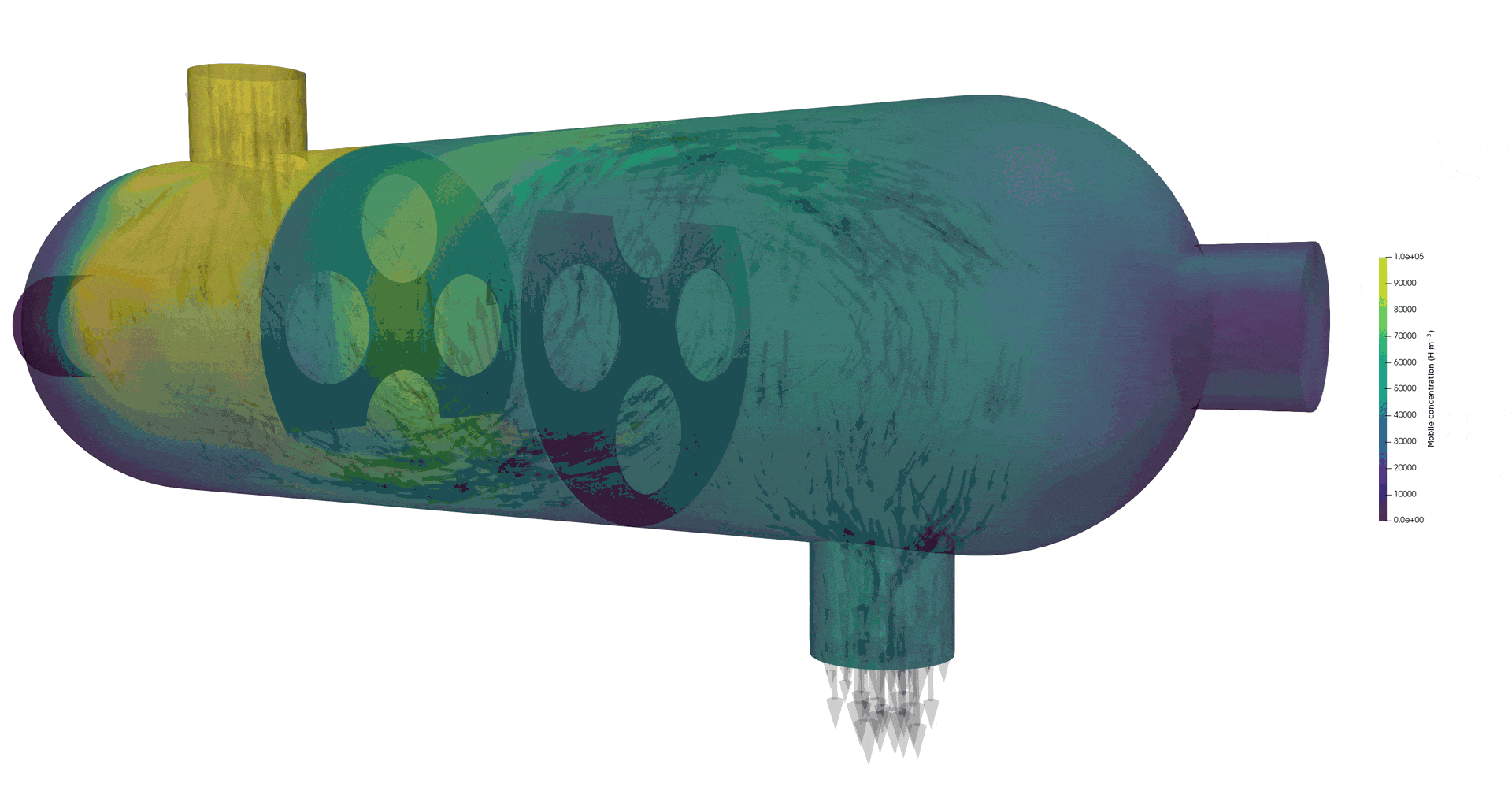
Tritium contamination in a heat exchanger
\( c = K_H \ P_\mathrm{up} \)
\( c = 0 \)
Permeation through the crucible wall
FLiBe
2D permeation through molten salts

HYPERION permeation rig
Tritium Breeding Blanket



- DEMO WCLL
- Complex 3D geometry
- Coupled to fluid dynamics
- Tritium generation in the LiPb volume (computed from neutronics)
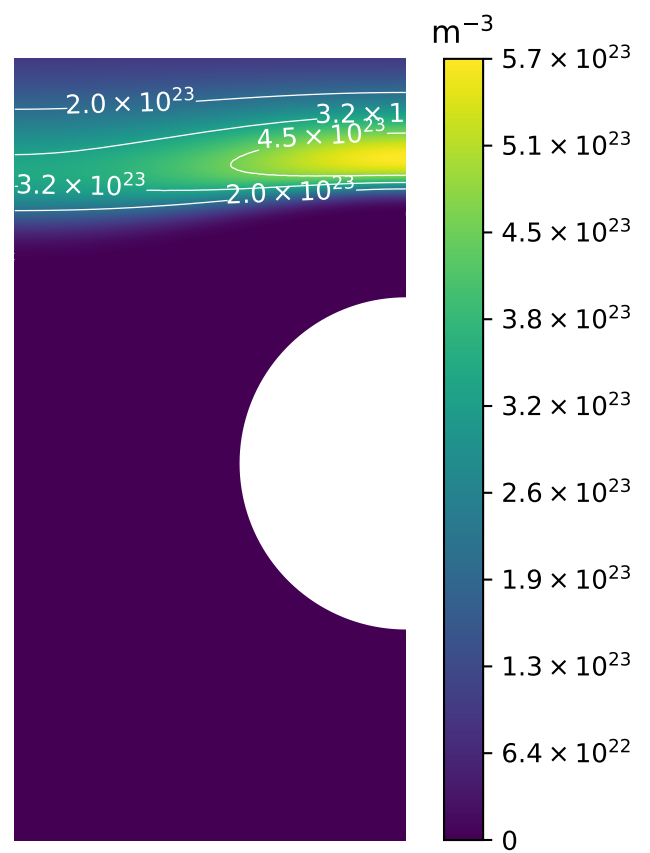
LIBRA produces validation data for multiphysics models



Tritium production map from neutronics (OpenMC)
Tritium concentration field (FESTIM)
Max conc. 1.4E13 T/m3
[T/n/cm3]

Natural convection neglected
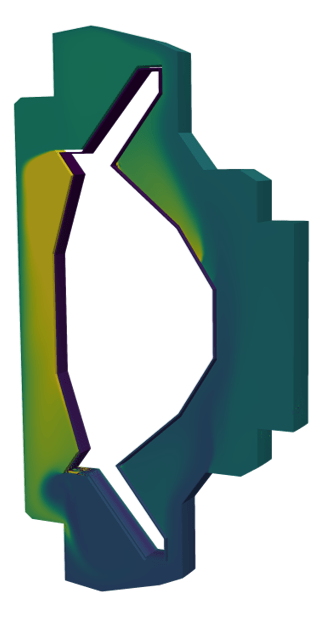



ARC Breeding Blanket
ARC blanket geometry
T source
Heat source
Velocity
Temperature
Turbulent viscosity
Tritium concentration
Tritium extraction system

- Permeation Against Vacuum
- Complex 3D geometry
- Coupled with fluid dynamics
- Tritium extraction from permeable membranes

HISP project: coupling FESTIM to plasma codes



RISP pulse
ITER FW divided in 60 bins
Data from DINA


Goal: find the best strategy for minimising ITER T inventory
HISP project: coupling FESTIM to plasma codes





10 DT FP pulses
ICWC + RISP
GDC
Simulation time:
~ 60 s per bin (~ hour full reactor)
Question time!
FESTIM hands-on workshop
User inputs
- Material properties
- Trap properties
- Geometry
- Boundary conditions
- Initial conditions
- ...
Heat transfer model
Hydrogen transport model
- McNabb & Foster
- Multi-level trapping
- Multi-isotopes
- ...
FESTIM
Outputs
- H concentration fields \(c(x,t)\)
- Temperature field \(T(x,t)\)
- surface fluxes
- inventories
- average concentration
- ...

2019
Start of development
We need a new tool!
Problem: predict T retention and permeation
- Multi-dimensional
- Multi-material
- non homogeneous temperature
W
Cu
CuCrZr
Particle and heat fluxes


Convection
14 mm

2022
License Apache 2.0

✅ More transparency
- Reproducibility in papers
- Source code available
✅ More collaborations
- No need for complex collaboration agreements
- External contributions
✅ More flexibility
- Can be adapted to your needs
- Better interoperability
2019
Open source
We need a numerical tool
Problem: predict T retention and permeation
- Multi-dimensional
- Multi-material
- non homogeneous temperature
W
Cu
CuCrZr
Particle and heat fluxes


Convection
14 mm
2022
License Apache 2.0

✅ More transparency
- Reproducibility in papers
- Source code available
✅ More collaborations
- No need for complex collaboration agreements
- External contributions
✅ More flexibility
- Can be adapted to your needs
- Better interoperability
Oct 2023
v1.0 release
2019
v1.0 release
We need a numerical tool
Problem: predict T retention and permeation
- Multi-dimensional
- Multi-material
- non homogeneous temperature
W
Cu
CuCrZr
Particle and heat fluxes


Convection
14 mm
2022
Oct 2023
April 2024

Non-profit organisation supporting open source software for science and research
More info at numfocus.org
2019
We need a numerical tool
Problem: predict T retention and permeation
- Multi-dimensional
- Multi-material
- non homogeneous temperature
W
Cu
CuCrZr
Particle and heat fluxes


Convection
14 mm
2022
Oct 2023

April 2024
Non-profit organisation supporting open source software for science and research
More info at numfocus.org
Meet the development team
Jonathan Dufour
CEA, France
+ other contributors






FESTIM is open-source
✅ More transparency
✅ More collaborations
✅ More flexibility

The code is missing a feature?
Just add it!
Found a bug?
Report it and we'll fix it!

FESTIM is open-source

Open-Source Software for Fusion Energy 2026 conference
Call for abstracts open!
FESTIM's development workflow
- Anyone can create their own copy (fork) of the FESTIM repository and make changes
- PRs are a place where FESTIM's maintainers review the proposed changes
- ~500 tests are automatically run
- The PR is only merged when all the tests pass ✅

fork
fork
pull request
FESTIM
Jane Doe
FESTIM
John Doe
FESTIM
festim-dev
pull request
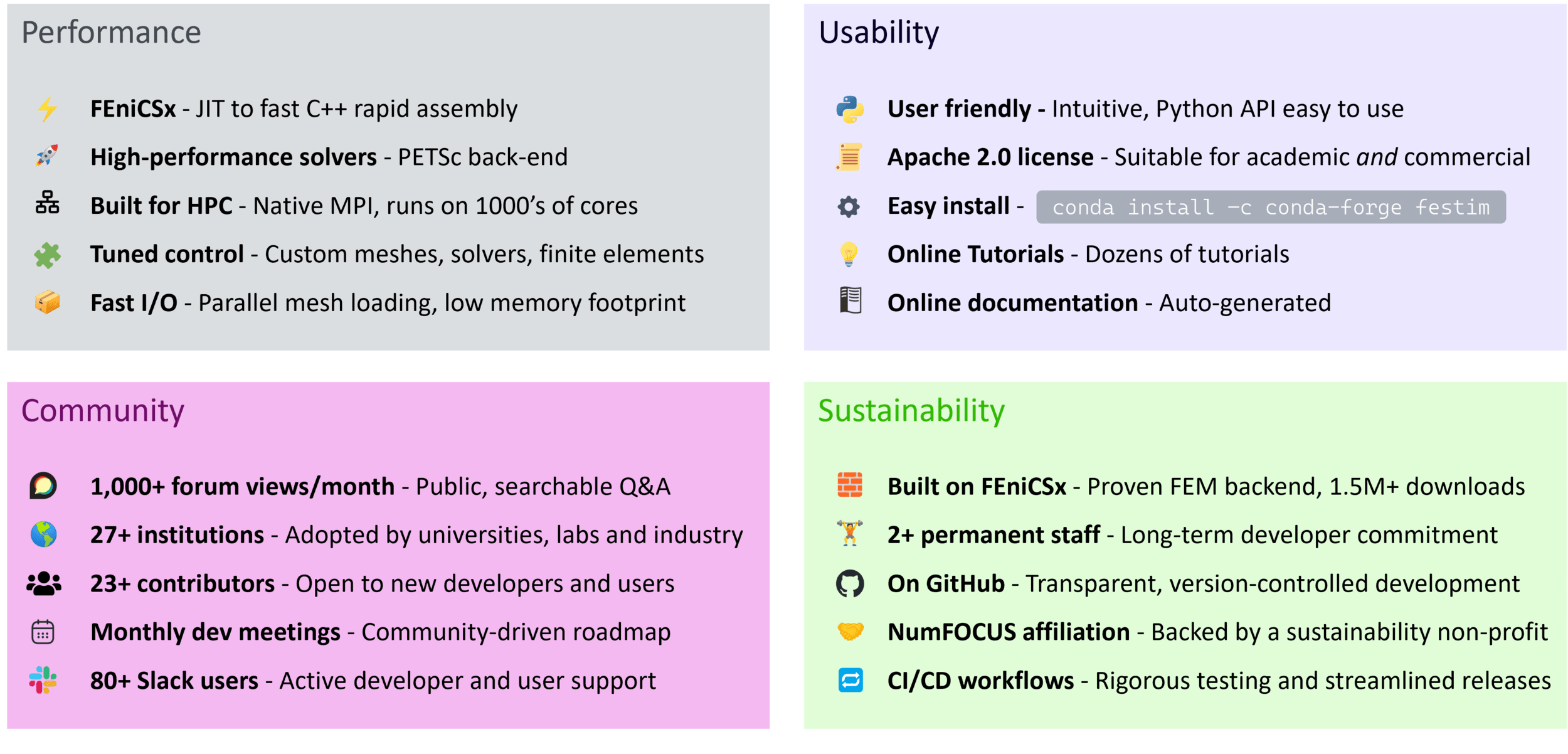
FESTIM is user-friendly

- Very easy to learn
- Plenty of libraries (numpy, scipy, matplotlib, HTM...)
- Inuitive interface
conda install -c conda-forge festimOne-line install!
import festim as F
import numpy as np
my_model = F.Simulation()
my_model.mesh = F.MeshFromVertices(
vertices=np.linspace(0, 1e-6, num=1001)
)
my_model.materials = F.Material(id=1, D_0=1.9e-7, E_D=0.2)
my_model.T = 500 # K
my_model.boundary_conditions = [
F.DirichletBC(
surfaces=[1, 2],
value=1e15, # H/m3/s
field=0
)
]
my_model.settings = F.Settings(
absolute_tolerance=1e10,
relative_tolerance=1e-10,
final_time=100 # s
)
my_model.dt = F.Stepsize(0.1) # s
my_model.initialise()
my_model.run()
FESTIM is user-friendly
FESTIM is user-friendly

To date, 5 user workshops have been organised, covering:
- Basic usage
- Advanced usage
- Hackathons
- How to contribute
UKAEA Aug 2024
~60 attendees in total!
FESTIM is fully documented
Check out the complete documentation at
Installation instructions
User guide
- Development guide
- Tutorials
- Theory background
- API reference
FESTIM is verified & validated
-
Validated against TDS, permeation experiments...
-
Verified against analytical solutions in many different problems
- Online V&V book
festim-vv-report.readthedocs.io
Method of Exact Solution
governing equations
exact solutions
parameters (sources, BCs, ICs)
FESTIM
computed solutions
solve
run
compare
⚠️sometimes very complex!
Method of Manufactured Solutions
governing equations
manufactured solutions
source terms, BCs and ICs
FESTIM
computed solutions
compare
FESTIM is used worldwide

8 private companies
16 universities
18 research organisations



📈5 years of development
📑13+ publications
🗣️110+ citations
🧑💻24+ contributors
🏛️28+ institutions using the code
🧑💻80+ Slack members
⭐100+ stars on GitHub
FESTIM in numbers
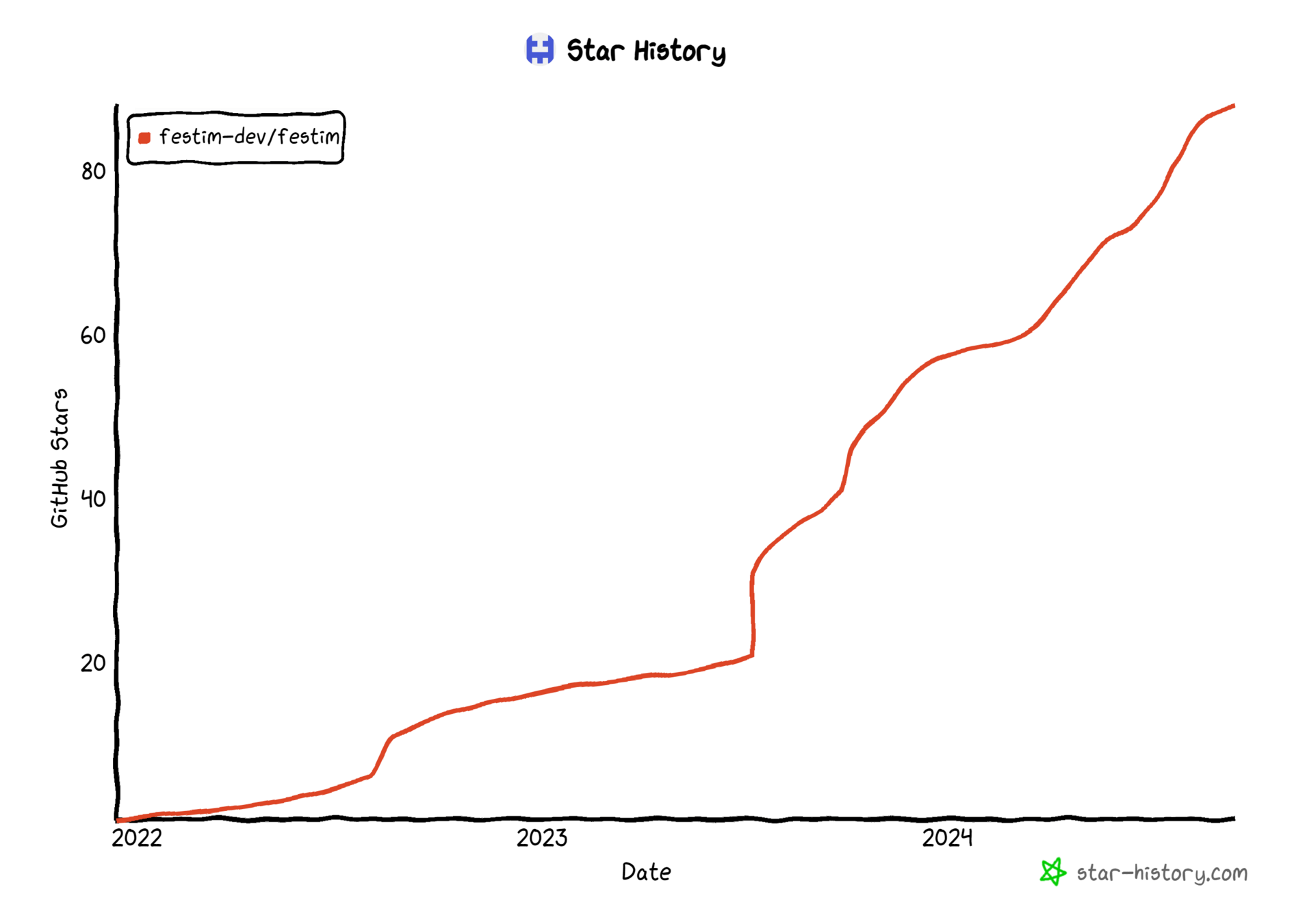
Evolution of GitHub stars
Open source
SOFE
New reference paper
Kyoto Fusioneering
UKAEA
Retention studies

- Delaporte-Mathurin et al 2024 International Journal of Hydrogen Energy 63 786–802
- Delaporte-Mathurin et al 2024 Nucl. Fusion 64 026003

- ITER plasma facing components
- Transient estimation of tritium retention
Influence of ELMs on retention

- 1D model of a ITER monoblock
- Transient heat transfer simulation
- Varying surface heat flux
Detritiation studies


Breeding Blanket modelling



- DEMO WCLL
- Complex 3D geometry
- Coupled to fluid dynamics
- Tritium generation in the LiPb volume (computed from OpenMC)
James Dark et al 2021 Nucl. Fusion 61 116076
Gas driven permeation

Surface limited regime
Bulk limited regime
Transition to bulk limited as the permeation number \( W \) increases
High H pressure
Low H pressure
Permeation flux
Permeation experiment

No barrier
with barrier
Permeation barrier
Substrate
High H pressure
Low H pressure
Conservation of chemical potential
Permeation flux
TDS analysis: neutron damage

- New proposed model for neutron-induced trap creation
- Parameterised on TDS data (self-damaged W)
TDS analysis: codeposits

- Simulation of W codeposited layers
- Influence of partial pressure
- 10 different traps!
Kinetic surface model
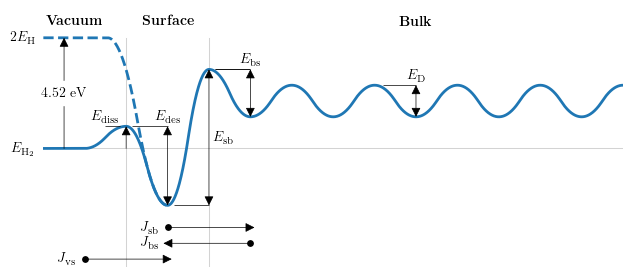
Kinetic surface model
- D in damaged W (S. Markelj JNM 2016)
- Comparison with NRA (Nuclear Reaction Analysis) profiles

Kinetic surface model
- H in oxidised W (A. Dunand et al 2022 Nucl. Fusion)
- Comparison with TDS spectra

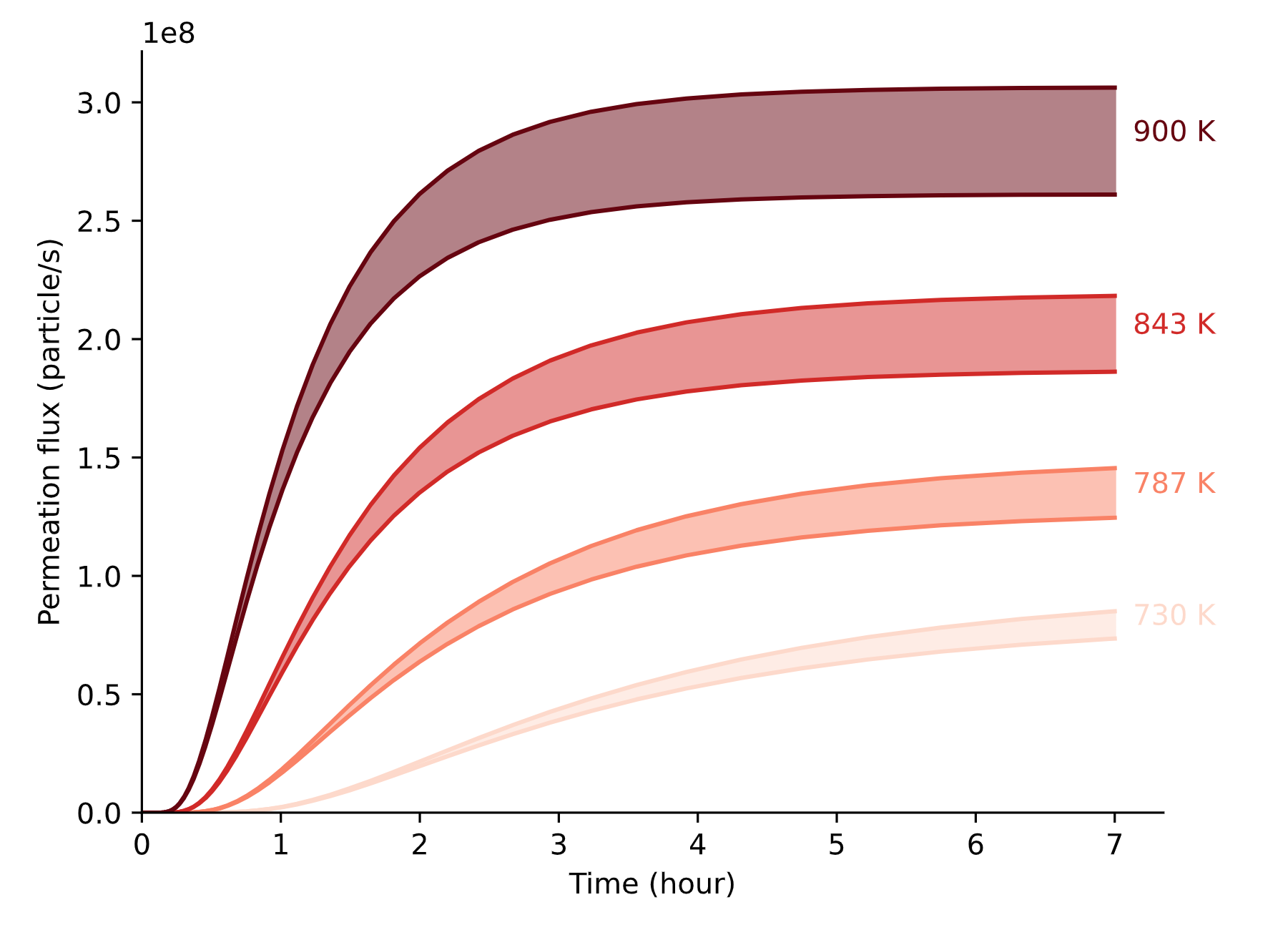
Kinetic surface model
- H in Ti (Hirooka et al 1981 JNM)
- Validation at 5 temperatures

H content (H/Ti)
HISP project: coupling FESTIM to plasma codes



RISP pulse
ITER FW divided in 60 bins
Data from DINA


Goal: find the best strategy for minimising ITER T inventory
HISP project: coupling FESTIM to plasma codes





10 DT FP pulses
ICWC + RISP
GDC
Simulation time:
~ 60 s per bin (~ hour full reactor)
Demo: how to install FESTIM
Demo: how to run a python script
Great python tutorial: swcarpentry.github.io/python-novice-inflammation
FESTIM tutorials
- Simple simulation
- TDS simulation
- Simple permeation simulation
- Visualisation and post-processing
- Radioactive decay