An Integrated Implementation of
Probabilistic Graphical Models
2020
Renato Cordeiro Ferreira
Advisor: Alan Mitchel Durham
IME-USP
https://renatocf.xyz/masters-defense-live
Our goal was to present a
new integrated implementation
of Probabilistic Graphical Models
for sequence labeling and alignment
Results
Review of Probabilistic Graphical Models
New summary of PGMs that make sequence labeling and alignment with their definitions and relationships
SECRETARY pattern
New design pattern to decrease coupling while keeping reusability of code
Refactoring of ToPS framework
New architecture and domain specific language that make it easier to extend the framework with new models
Results
Generalized Covariance Model
New model that recognizes a subset of context-free and context-sensitive languages, replacing two specialized models (CMs, CSHMMs) with extended capabilities and the same or better time/space algorithmic efficiency
Generalized Multi-Sequence Hidden Markov Model
New model that makes sequence labeling and alignment with an integrated set of algorithms, replacing four specialized models (HMMs, GHMMs, PHMMs, GPHMMs) with the same time/space algorithmic efficiency
Probabilistic
Graphical Models
Joint distribution:
Probability distribution \( P(Y_1, \ldots, Y_m, X_1, \ldots, X_n) \) which can be queried to reason over the model:
- Map assignment: \( \mathrm{MAP}(\mathbf{Y} \mid \mathbf{X} = \mathbf{x}) = \mathrm{arg\,max}_{\mathbf{y}} P(\mathbf{y}, \mathbf{x}) \)
- Posterior probability distribution: \( P(\mathbf{Y} \mid \mathbf{X} = \mathbf{x}) \)
Definitions
Probabilistic Model:
A model that is mathematically described using random variables, i.e., functions that map events of a given
sample space to a discrete or continuous space
Sickness diagnosis problem:
Set of patients \( P \)
- Sick? \( S: P \rightarrow \{0, 1\} \)
- Fever? \( T: P \rightarrow \{0, 1\} \)
- Hypertension? \( B: P \rightarrow \{0, 1\} \)
Queries:
Given a patient has fever and hypertension
- Is he sick or not? \( \mathrm{MAP}(S \mid B = 1, T = 1) \)
- How likely is he sick? \( P(S = 1 \mid B = 1, T = 1) \)
output
input
input
Example
Probabilistic Graphical Model (PGM):
A probabilistic model that uses a graph to compactly describe the dependencies between random variables and show a factorization of their joint distribution
Bayesian Network (BN):
A PGM whose graph is a directed acyclic graph (DAG)
Markov Network (MN):
A PGM whose graph has only undirected edges
Definitions
Generative model:
A probabilistic model that factorizes \( P(\mathbf{Y}, \mathbf{X}) \) between the output variables \( \mathbf{Y} \) and the input variables \( \mathbf{X} \)
Discriminative model:
A probabilistic model that factorizes \( P(\mathbf{Y} \mid \mathbf{X}) \) between the output variables \( \mathbf{Y} \) and the input variables \( \mathbf{X} \)
Generative and discriminative equivalents:
Every generative PGM has a discriminative equivalent that is structurally equal but represents a different distribution
Definitions
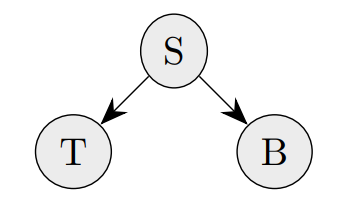
Bayesian Network:
A BN for the sickness diagnosis example
(arrows indicate states that influence others)


It expresses a factorization in terms of
Conditional Probability Distributions (CPDs):
\( P(S, T, B) = P(S) P(T | S) P(B | S) \)
Generative
Example
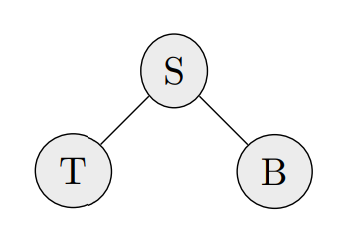
Markov Network:
A MN for the sickness diagnosis example
(edges indicate that there is a connection)
It expresses a factorization in terms of Factor Functions \( \Phi(C_i): \mathrm{Im}(C_i) \longrightarrow \mathbb{R}^+ \) where \( C_i \) is a click of the graph: \( P(S, T, B) \propto \Phi(S) \Phi(T, S) \Phi(B, S) \Phi(T) \Phi(B) \)
Generative


Example
Conditional Random Field:
A Markov Network that ignores clicks related only input variables (to avoid their complexity)
This expresses a factorization in terms of Factor Functions \( \Phi(C_i): \mathrm{Im}(C_i) \longrightarrow \mathbb{R}^+ \) where \( C_i \) is a click of the graph: \( P(S \mid T, B) \propto \Phi(S) \Phi(T, S) \Phi(B, S) \)

Discriminative


Example
Generative
\( P(S \mid T, B) \propto \)
\( \Phi(S) \Phi(T, S) \Phi(B, S) \)


Discriminative
\( P(S, T, B) = \)
\( P(S) P(T \mid S) P(B \mid S) \)
Generalizes better
with less data
Generalizes better
with more data
Generative vs Discriminative
Models dependencies
between input variables \(P(\mathbf{X})\)
Requires less knowledge
about the domain described
Ignores dependencies
between input variables \(P(\mathbf{X})\)
Can generate sequences to simulate the process described
Structured prediction:
The outcome of the queries over the model represent the structure of a complex object (such as a text or an image) in opposition to a single value
Sequence labeling:
Classify the elements of a sequence in a set of categories
Sequence alignment:
Find the best match between positions of 2+ sequences
Definitions

Casino with game of dice passing through a heist:
- Fair Die: \( P(s) = 1/6 \) for all \( s \)
- Loaded Die: \( P(1) = 1/2 \)
Refund when it can prove the dice was tempered
Sequence labeling:
Given a sequence of rolls produced by a player:
- When was the die tampered? (MAP assignment)
- What is the most likely status of the die on each turn of the game? (Posterior probability)
6 1 4 4 1 2 3 4 6 6 6 2 2 4 6
F F F L L F F F F F F L L L L
Example

New game of dice in the Casino
Players win more money the longest the match between their sequence of guesses and the casino's sequence of rolls
Sequence alignment:
Given a sequence of rolls made by the casino:
And a sequence of guesses produced by a player:
- What is the best match between the players' guesses and the casino's rolls?
6 1 4 4 1 2 3 4 6 6 6 2 2 4 6
6 1 2 2 4 1 4 3 4 6 6 6 1 2 4 6
Example

New game of dice in the Casino.
Players will win extra money if they produce palindrome (abccba) or copy (abcabc) subsequences within their sequence of rolls
Sequence labeling:
Given a sequence of rolls produced by a player during the game:
- Where are the palindromes or copy subsequences?
- How to produce the longest subsequences?
6 1 4 4 1 2 3 4 6 6 6 2 2 4 6
Example
We created a summary of the
relationships between
PGMs that make sequence
labeling and alignment
PGMs for sequence labeling and alignment:
Subcategories of Bayesian and Markov Networks:
| Hidden Markov Model | HMM |
| Generalized Hidden Markov Model | GHMM |
| Pair Hidden Markov Model | PHMM |
| Generalized Pair Hidden Model | GPHMM |
| Stochastic Context-Free Grammar | SCFG |
| Covariance Model | CM |
| Context-Sensitive Hidden Markov Model | CSHMM |
| Linear Chain Conditional Random Field | LCCRF |
| Semi-Markov Conditional Random Field | Semi-CRF |
BN
MN
Reg
CF
Reg
CS
Definitions
Dynamic
Bayesian Network
Conditional
Random Field
Hidden
Markov Model
+ Discrete vars.
+ Linear out. vars.
Probabilistic Graphical Model
Bayesian Network
Markov Network
+ DAG
+ Undirected edges
+ Show process through time
+ Ignore deps. between in. vars.
Naive Bayes
Logistic Regression
+ 1 out. var.
+ 1 out. var.
Linear-Chain
CRF
Generalized HMM
+ decouple
duration
Pair Hidden
Markov Model
Generalized Pair HMM
Semi-Markov
CRF
+ Multiple sequences
+ Multiple sequences
Context-Sensitive HMM
Stochastic Context-Free Grammar
+ Memory between states
SEQUENCE LABELING
SEQUENCE ALIGNMENT
GENERATIVE
DISCRIMINATIVE
+ decouple
duration
+ decouple
duration
+ Formal Language
HIGHER DESCRIPTIVE POWER
Covariance
Model
Hierarchy of Mathematical Assumptions
ToPS
Framework
Background
ToPS: Toolkit of Probabilistic Models of Sequence
C++ framework created to implement models that solve sequence labeling and alignment problems in the field of Bioinformatics (genomics, proteomics, transcriptomic)
MYOP: Make Your Own Predictor
ToPS was originally created as a base for MYOP, which uses it to find genes and transcripts in DNA sequences
40
Classes
10k
Lines of Code
14
Models
Single Object-Oriented Hierarchy
ToPS implements all its probabilistic models using the COMPOSITE pattern to improve the reuse of code
Specification Language
ToPS provides a DSL to describe probabilistic models in a mathematical way instead of creating them with code
Command Line Applications
ToPS provides a set of Unix-style binaries to execute different tasks with the models
Characteristics
| Model | Acronym |
|---|---|
| Discrete and Idependent Distribution | IID |
| Inhomogeneous Markov Chain | IMC |
| Maximal Dependence Decomposition | MDD |
| Multiple Sequential Model | MSM |
| Periodic Inhomogeneous Markov Chain | PIMC |
| Similarity Based Sequence Weighting | SBSW |
| Variable Length Markov Chain | VLMC |
| Hidden Markov Model | HMM |
| Generalized Hidden Markov Model | GHMM |
PGMs
Distributions
Published Probabilistic Models
| Model | Acronym |
|---|---|
| Pair Hidden Markov Model | PHMM |
| Generalized Pair Hidden Markov Model | GPHMM |
| Context-Sensitive Hidden-Markov Model | CSHMM |
| Linear Chain Conditional Random Field | LCCRF |
| Semi-Markov Conditional Random Field | Semi-CRF |
Each model had minor differences that affected the framework implementation, resulting in technical debt
Vitor Onuchic
Rafael Mathias
Ígor Bonadio
Extensions after publication
Technical Debt
Difficult Extensibility
Bad design smells make it difficult to add new models
Legacy Code
Code base written in C++98 with outdated practices
Limited Domain Specific Language
DSL does not support complex structures for CRFs
Memory Overhead
Insufficient caching increases use of memory unnecessarily
Published ToPS'
Architecture
Language
Models
App
Published ToPS' Architecture
Factories
Language
Models
App
Published ToPS' Architecture
Factories
ToPS' command-line applications, allowing end users to execute tasks on the probabilistic models
Language
Models
App
Published ToPS' Architecture
Factories
ToPS' main component.
It holds all algorithms for probabilistic models
whose calculations use
an string alphabet
Language
Models
App
Published ToPS' Architecture
Factories
Language component.
It holds an abstract syntax tree for a domain specific language (DSL) that describes models
Language
Models
App
Published ToPS' Architecture
Factories
Factories component. It holds all algorithms that train or load pretrained models in the framework

PGMs
Published ToPS' Hierarchy of Probabilistic Models
Decorators
Distributions
Interface

Unfactored interface
Unfactored
implementation
Unfactored interface and implementation
Multifaceted abstraction
Multifaceted abstraction
Published ToPS' Hierarchy of Probabilistic Models
Published ToPS' Hierarchy of Factories of Probabilistic Models
Multifaceted abstraction
Imperative
Abstraction
Imperative
Abstraction
Imperative
Abstraction
Rebel Hierarchy
Imperative Abstraction
We created a new architecture for the framework to solve the technical debt and make it
easy to extend in the future
Refactored ToPS'
Architecture
Lang
Config
Model
Exception
App
Refactored ToPS' Architecture
Lang
Config
Model
Exception
App
ToPS' command-line applications, allowing end users to execute tasks on the probabilistic models
Refactored ToPS' Architecture
Lang
Config
Model
Exception
App
ToPS' main component. It holds all code for probabilistic models as an independent shared library
All probabilistic models make their calculations based on a discrete numeric alphabet
Refactored ToPS' Architecture
Lang
Config
Model
Exception
App
ToPS' language component.
It holds the implementation of a domain specific language (DSL)
to describe probabilistic models
ToPS' DSL is based on ChaiScript, an embedded script language designed to be integrated with C++
Refactored ToPS' Architecture
Lang
Config
Model
Exception
App
ToPS' auxiliary layer. It holds a C++ based intermediate representation of probabilistic models
ToPS' config structures store parameters to train and define of probabilistic models
Refactored ToPS' Architecture
Lang
Config
Model
Exception
App
ToPS' exceptions, representing all errors that can happen during the execution of ToPS
Refactored ToPS' Architecture
Model
tops::model





\(P(\mathbf{x})\)
Evaluate
Calculate the probability of
a sequence given a model
Generate
Draw random sequences
from a model
Train
Estimate parameters of the
model from a dataset
Serialize
Save parameters of a model
for later reuse
Calculate
Find the posterior probabilities
for an input sequence
Label
Find the MAP assignment
for an input sequence
PGMs only
Behaviors





\( P(\mathbf{x}) \)
Probabilistic Models
(COMPOSITE)
Trainer
Evaluator
Generator
Serializer
Calculator
Labeler
New Architecture
We found and documented
a new design pattern
that decreases coupling while keeping the reusability of code

Boss
- Has multiple behaviors

Secretary
- Represents only one behavior
- Has multiple secretaries
- Represents only one boss
- Is used indirectly by clients
- Interacts directly with clients
- Holds data shared among behaviors
- Keeps all the code that implements behaviors
- Holds data used only by the behavior they represent
- Keeps no meaningful logic, forwarding calls to its boss
[1] R. C. Ferreira, Í. Bonadio, and A. M. Durham, “Secretary pattern: decreasing coupling while keeping reusability”,
Proceedings of the 11th Latin-American Conference on Pattern Languages of Programming. The Hillside Group, p. 14, 2016.
SECRETARY pattern¹

SECRETARY: Sequence diagram
1
2
3
5
1
2
3
5
3
4
4





\( P(\mathbf{x}) \)
Probabilistic Models
(COMPOSITE)
Trainer
Evaluator
Generator
Serializer
Calculator
Labeler
New Architecture
Secretary
Secretary
Secretary
Secretary
Secretary
Secretary
Boss

PGMs
Distributions
Interface + CRTP
Interface + CRTP
Distributions
Decorators
Refactored ToPS' Hierarchy of Probabilistic Models
tops::model::ProbabilisticModel
Root of the hierarchy, it implements four secretaries:
trainer, evaluator, generator, and serializer
tops::model::DecodableModel
It descends directly from ProbabilisticModel and implements all parent's secretaries plus calculator and labeler
tops::model::ProbabilisticModelDecorator
It descends directly from ProbabilisticModel and extends the functionalities of other models
Model Hierarchy: Interfaces
The curiously recurring template pattern (CRTP) is an idiom in C++ in which a class X derives from a class template instantiation using itself as template argument. [...] Some use cases for this pattern are static polymorphism and other metaprogramming techniques [...].
Wikipedia , Curiously Recurring Template Pattern
tops::model::ProbabilisticModelCRTP
tops::model::DecodableModelCRTP
tops::model::ProbabilisticModelDecoratorCRTP
Implement FACTORY METHOD's for secretaries, define virtual methods that secretaries delegate to, and host code reused between subclasses
Model Hierarchy: CRTP
Optimization Challenges
Code Replication
ToPS has small optimizations spread throughout its codebase, e.g., probability operations in logarithmic space
Memory Management
ToPS uses large matrices that often do not fit in the available memory
Memory Overhead
ToPS has many algorithms whose results can be precached to improve their efficiency
https://github.com/renatocf/probability
https://github.com/renatocf/multivector
probability
- Implements probability operations in log space
multivector
- Implements multidimensional arrays in contiguous memory
- Allows algorithms to be
written closer to their
math representation
- Allows algorithms to create
and manipulate matrices
similarly to C++ std::vector
Efficient Implementation
Libraries introduce optimizations using OOP abstractions
Lang
tops::lang

Definition
Represents trained parameters for a given model

Training
Represents training parameters for a given model
ToPS implements a specification language with configuration files to train and define probabilistic models
Specification Language
// Casino Heist Example
model_type = "HMM"
observations = [ "1", "2", "3", "4", "5", "6" ]
labels = [ "Fair", "Loaded" ]
initial_probabilities = [
"Fair" : 0.5,
"Loaded" : 0.5
]
transition_probabilities = [
"Loaded" | "Fair" : 0.1,
"Fair" | "Fair" : 0.9,
"Fair" | "Loaded" : 0.1,
"Loaded" | "Loaded" : 0.9
]
emission_probabilities = [
"1" | "Fair" : 1.0/6,
"2" | "Fair" : 1.0/6,
"3" | "Fair" : 1.0/6,
"4" | "Fair" : 1.0/6,
"5" | "Fair" : 1.0/6,
"6" | "Fair" : 1.0/6,
"1" | "Loaded" : 1.0/2,
"2" | "Loaded" : 1.0/10,
"3" | "Loaded" : 1.0/10,
"4" | "Loaded" : 1.0/10,
"5" | "Loaded" : 1.0/10,
"6" | "Loaded" : 1.0/10
]
HMM
Casino Heist
Config file composed of:
- Strings
- Lists
- Maps
- Numbers
It is simple to create a parser to read this configuration file
// Cassino Heist definition
model_type = "LCCRF"
observations = [ "1", "2", "3", "4", "5", "6" ]
labels = [ "Fair", "Loaded" ]
feature_function_libraries = [
lib("features.tops")
]
feature_parameters = [
"label_loaded": 1.0,
"label_fair": 2.0
]LCCRF
Casino Heist
// Cassino Heist definition
model_type = "LCCRF"
observations = [ "1", "2", "3", "4", "5", "6" ]
labels = [ "Fair", "Loaded" ]
feature_function_libraries = [
lib("features.tops")
]
feature_parameters = [
"label_loaded": 1.0,
"label_fair": 2.0
]
- Strings
- Lists
- Maps
- Numbers
Config file composed of:
- Libraries
Libraries complicate creating a parser
// Cassino Heist definition
model_type = "LCCRF"
observations = [ "1", "2", "3", "4", "5", "6" ]
labels = [ "Fair", "Loaded" ]
feature_function_libraries = [
lib("features.tops")
]
feature_parameters = [
"label_loaded": 1.0,
"label_fair": 2.0
]LCCRF
Casino Heist
// Feature Function Library
observations = [ "1", "2", "3", "4", "5", "6" ]
labels = [ "Loaded", "Fair" ]
// Feature functions built directly
feature("label_loaded", fun(x, yp, yc, i) {
if (yc == label("Loaded")) {
return 1;
} else {
return 0;
}
})
feature("label_fair", fun(x, yp, yc, i) {
if (yc == label("Fair")) {
return 1;
} else {
return 0;
}
})
// Feature function prototypes
use("prototypes.tops")
// Feature functions built from factory
indicator("Fair" -> "Fair"))
indicator("Fair" -> "Loaded"))
indicator("Loaded" -> "Fair"))
indicator("Loaded" -> "Loaded"))
-
Functions
(with any logic)
Libraries composed of:
-
Templates
(factories of functions)
We need a
full-featured programming language
We reimplemented the DSL
based on ChaiScript to make it
a full-featured programming
language that supports CRFs
Integrated
Algorithms
6 1 4
F F F
F F L
F L F
F L L
L F F
L F L
L L F
L L L
Common calculation
can be reused!
Labeling sequences
How to calculate the most likely labeling?
Labeling with
common prefix
Factorization with
Markovian property
1: 1/6
2: 1/6
3: 1/6
4: 1/6
5: 1/6
6: 1/6
1: 1/2
2: 1/10
3: 1/10
4: 1/10
5: 1/10
6: 1/10
0.1
0.1
0.9
0.9
F
L
HMM for the
Casino Heist example
Considering rolls 614
Algorithms with Dynamic Programming!
Viterbi:
Calculates the MAP assignment using a dynamic programming algorithm over an input sequence
for models equivalent to regular grammars
Forward-Backward:
Calculates the posterior probability distribution
by combining the forward and backward dynamic programming algorithms over an input sequence
for models equivalent to regular grammars
Algorithms (Regular)
def HMM::viterbi(x)
# Initialization
γ = NArray.zeros(@states.len, x.len)
γ[@begin, 0] = 1
# Iteration
for j in 1..x.len do
for k in @states do
i = j - 1
for p in k.predecessors do
prob = γ[p, i]
∗ p.τ(k)
∗ k.ε(x[i..j])
if (prob > γ[k, j]) then
γ[k, j], π[k, j] = prob, p
# Termination
best = γ[@end, x.len]
y = traceBack(x, γ, π)
return best, y, γMemory: \( O(SL) \)
Time: \( O(LSC) \)
S
L
L
S
L
C
Basic model for sequence labeling
HMM's Viterbi
x
j
j-1
k
p
γ[p][j-1]
ε(x[j])
τ(p)

Iterate until finding the best labeling sequence
Generalized HMM
It decouples the concept of duration from transitions,
which allows the model to have:
- any distribution for duration
- any probabilistic model for emission
Pair HMM
It receives two sequences to make an alignment
Extending HMMs
Generalized Pair HMM
It has both extensions presented previously
We created a new model
that makes all HMM extensions
with the same time/space algorithmic efficiency
Generalized
It decouples the concept of duration from transitions,
which allows the model to have:
- any distribution for duration
- any probabilistic model for emission
Multi-Sequence
It receives one or more sequences as input and can make:
- sequence labeling for a single sequence
- sequence alignment for multiple sequences
Generalized Multi-Sequence HMM
def GMHMM::viterbi(xs)
# Initialization
γ = NArray.zeros(@states.len, *xs.map(|x| x.len))
γ[@begin, *xs.map(|x| 0)] = 1
# Iteration
for js in *xs.map(|x| 1..x.len) do
for k in @states do
dss = k.ds.zip(js)
.each_with_index.reduce([])
{|pd,j,z| pd(1, [j, @mbt].min) if k.emits?(z)}
for ds in Array.product(*dss) do
is = js.zip(ds)
.each_with_index.map
{ |j,d,idx| j - d * k.Δ(idx) }
es = xs.zip(is).zip(js)
.each_with_index.reduce([])
{ |x,i,j,idx| x[i..j] if k.emits?(idx) }
for p in k.predecessors do
prob = γ[p, *is]
∗ p.τ(k)
∗ k.δs(*ds)
∗ k.εs(*es)
if (prob > γ[k, *js]) then
γ[k, *js], π[k, *js] = prob, { p, ds }
# Termination
best = γ[@end, *xs.map(|x| x.len)]
y = traceBack(xs, γ, π)
return best, y, γLᴺ
Lᴺ
S
Lᴺ
C
Memory: \( O(SLᴺ) \)
Time: \( O(LᴺSBᴺC) \)
Bᴺ
GPHMM for multiple sequences
GMHMM's Viterbi
S

Iterate until finding the best labeling sequence
x₀
j₀
i₀
k
p
γ[p, i₀, i₁]
ε(x₀[i₀..j₀], x₁[i₁..j₁])
τ(p)
x₁
j₁
i₁
ε(x₀[i₀..j₀], x₁[i₁..j₁])
γ[p, i₀, i₁]
d₀
d₁
δ(d₀)
δ(d₁)
x₀[i₀..j₀]
x₁[i₁..j₁]
HMM
Generalized
Multi-Sequence

GMHMM
can implement all
optimizations
from the specialized
models so that its
time and space
algorithmic complexity
is equivalent to theirs
CYK (Cocke-Younger-Kasami):
Calculates the MAP assignment using a dynamic programming algorithm over an input sequence
for models equivalent to context-free grammars
Inside-Outside:
Calculates the posterior probability distribution
by combining the forward and backward dynamic
programming algorithms over an input sequence
for models equivalent to context-free grammars
Algorithms (Context-Free)
def CM::cyk(x)
# Initialization
γ = NArray.zeros(@states.len, x.len, x.len)
(1..x.len).each { |j| γ[@begin, j, j] = 1 }
# Iteration
for j, i in 1..x.len, j..2 do
for k in @states do
l, r = i + k.Δ(:L), j - k.Δ(:R)
if not k.bifurcation? then
for child in k.children do
curr = γ[child, l, r] * p.τ(k.child)
prob = [curr, prob].max
else
for cut in (l..r) do
curr = γ[k.left, l, cut] * p.τ(k.left)
∗ γ[k.right, cut, r] ∗ p.τ(k.right)
prob = [curr, prob].max
prob *= k.ε(x[i..l], x[r..j])
if (prob > γ[k, i, j]) then
γ[k, i, j], π[k, j, j] = prob, p
# Termination
best = γ[@end, 0, x.len]
y = traceBack(x, γ, π)
return best, y, γS
L
L²
S
L
L
Memory: \( O(SL²) \)
Time: \( O(L^2S_1C+L^3S_2) \)
S₁
S₂
C
L
Basic context-free model for labeling
CM's CYK
#1: Start, End, Left, Right, Pairwise, Delete
#2: Bifurcation
Depending on the type of state:
Iterate until finding the best labeling tree

i
j
l
r
k
c₁
x
x[i..l]
x[r..j]
c₂
q
x[l..q]
x[q ..r]
τ(c₂)
τ(c₁)
γ[c₁, l, q]
γ[c₂, q, r]
ε(x[i..l], x[r..j])
c
γ[c, l, r]
τ(c)
Generalized CM
It decouples the concept of duration from transitions,
which allows the model to have:
- any distribution for duration
- any probabilistic model for emission
Pair CM
It receives two sequences to make an alignment
Extending CMs?
Pair CMs make no sense because CMs represent profiles
We created a new model
that generalizes CMs and
can represent context-free and context-sensitive languages

GCM is more efficient than CSHMMs
to represent simple context-sensitive languages (languages that can represent copy subsequences)
def GCM::cyk(x)
# Initialization
γ = NArray.zeros(@states.len, x.len, x.len)
(0..x.length).each { |j| γ[@begin, j, j] = 1 }
# Iteration
for j, i in 1..x.length, j..2 do
for k in @states do
dss = {}
dss[:L] = k.ds[:L](1, [j-i+1, @mbt].min)))
dss[:R] = k.ds[:R](1, [j-i+1, @mbt].min)))
for ds in *dss do
l, r = i + ds[:L]*k.Δ(:L), j - ds[:R]*k.Δ(:R)
if not k.bifurcation? then
for child in k.children do
curr = γ[child, l, r] ∗ p.τ(k.child)
prob = [curr, prob].max
else
for cut in (l..r) do
prod = γ[k.left, l, cut] * p.τ(k.left)
∗ γ[k.right, cut, r] ∗ p.τ(k.right)
prob = [curr, prob].max
prob *= δ(*ds) * k.ε(x[i..l], x[r..j])
if (prob > γ[k, i, j]) then
γ[k, i, j], π[k, i, j] = prob, { p, d }
# Termination
best = γ[@end, 0, x.len]
y = traceBack(x, γ, π)
return best, y, γMemory: \( O(SL²) \)
Time: \( O(L^2S_1CB+L^2S_2L) \)
CM with non-geometric duration
GCM's CYK
S
L
L²
S
L
L
S₁
S₂
C
L
B
i
j
l
r
k
c₁
x
x[i..l]
x[r..j]
c₂
q
x[l..q]
x[q ..r]
τ(c₂)
τ(c₁)
γ[c₁, l, q]
γ[c₂, q, r]
ε(x[i..l], x[r..j])
c
γ[c, l, r]
τ(c)
d₁
d₂
δ(d₁)
δ(d₂)
#1: Start, End, Left, Right, Pairwise, Delete
#2: Bifurcation
Depending on the type of state:
Iterate until finding the best labeling tree

CM
Generalized
Conclusion
Results
Review of Probabilistic Graphical Models
New summary of PGMs that make sequence labeling and alignment with their definitions and relationships
SECRETARY pattern
New design pattern to decrease coupling while keeping reusability of code
Refactoring of ToPS framework
New architecture and domain specific language that make it easier to extend the framework with new models
Results
Generalized Covariance Model
New model that recognizes a subset of context-free and context-sensitive languages, replacing two specialized models (CMs, CSHMMs) with extended capabilities and the same or better time/space algorithmic efficiency
Generalized Multi-Sequence Hidden Markov Model
New model that makes sequence labeling and alignment with a single set of algorithms, replacing four specialized models (HMMs, GHMMs, PHMMs, GPHMMs) with the same time/space algorithmic efficiency
Future Work
Integration of CRFs
We enabled the fully integration of LCCRFs and Semi-CRFs to ToPS with the DSL based on ChaiScript
Implementation of GCM
We did not have time to provide an implementation of Generalized Covariance Models in the framework
Production-ready ToPS
We still need to finish the implementation of the framework so it can replace the published version of ToPS
An Integrated Implementation of
Probabilistic Graphical Models
2020
Renato Cordeiro Ferreira
Advisor: Alan Mitchel Durham
IME-USP
https://renatocf.xyz/masters-defense-live
Definitions
Model:
A simplified declarative representation that encodes the relevant elements of an experiment or real situation
Probabilistic Model:
A model that is mathematically described using random variables, i.e., functions that map events \( s \) of a given sample space \( \Omega \) to a discrete or continuous space
Example

Model:
\(N\) is the number of faces in the die (ignores color, material, etc.)
Algorithm:
Generate numbers in the interval \( [1, N] \) (simulate rolling the dice)
Probabilistic Model:
\( \Omega = \{1, \ldots, N\} \), \( P(s) = 1/N \)
\( Even: S \longrightarrow \{0,1\} \) (outcome is even)

Multidimensional Probabilistic Model:
Probabilistic model that describes a problem with a set of random variables \( \mathcal{X} = \{ Y_1, \ldots, Y_m, X_1, \ldots, X_n \} \)
Joint distribution:
Probability distribution \( P(\mathcal{X}) = P(Y_1, \ldots, Y_m, X_1, \ldots, X_n) \) which can be queried to reason over the model:
- Map assignment: \( \mathrm{MAP}(\mathbf{Y} \mid \mathbf{X} = \mathbf{x}) = \mathrm{arg\,max}_{\mathbf{y}} P(\mathbf{y}, \mathbf{x}) \)
- Posterior probability distribution: \( P(\mathbf{Y} \mid \mathbf{X} = \mathbf{x}) \)
Definitions
Chomsky's Hierarchy:
Hierarchy that describes four levels of descriptive power associated with transformational grammars and their corresponding formal languages and parsers:
| Level | Name | Associated Parser |
|---|---|---|
| L3 | Regular | Finite-state automaton |
| L2 | Context-Free | Push-down automaton |
| L1 | Context-Sensitive | Linear bounded automaton |
| L0 | Unrestricted | Turing machine |
Definitions

SECRETARY pattern: Class diagram





\( P(\mathbf{x}) \)
Probabilistic Models
(COMPOSITE)
Trainer
Estimates parameters of a model from a dataset
Evaluator
Calculates the probability of a sequence given a model
Generator
Draws random sequences from the model
Serializer
Saves parameters of the model for later reuse
Calculator
Finds the posterior probabilities
of an input sequence
Labeler
Finds the MAP assignment
for an input sequence
Boss
Secretary
Secretary
Secretary
Secretary
Secretary
Secretary
New Architecture
Factor functions can be implemented as any kind of procedure of a full-featured programming language

Factor functions:
\( \Phi(C_i): \mathrm{Im}(C_i) \longrightarrow \mathbb{R}^+ \)

How to represent CRFs?
Simulations
def HMM::viterbi(x)
# Initialization
γ = NArray.zeros(@states.len, x.len)
γ[@begin, 0] = 1
# Iteration
for j in 1..x.len do
for k in @states do
i = j - 1
for p in k.predecessors do
prob = γ[p, i]
∗ p.τ(k)
∗ k.ε(x[i..j])
if (prob > γ[k, j]) then
γ[k, j], π[k, j] = prob, p
# Termination
best = γ[@end, x.len]
y = traceBack(x, γ, π)
return best, y, γx
j
i
k
p
γ[p][i]
ε(x[i..j])
τ(p)

Iterate until finding the best labeling sequence
Memory: \( O(SL) \)
Time: \( O(LSC) \)
S
L
L
S
L
C
Basic model for sequence labeling
HMM's Viterbi
def GHMM::viterbi(x)
# Initialization
γ = NArray.zeros(@states.len, x.len)
γ[@begin, 0] = 1
# Iteration
for j in 1..x.len do
for k in @states do
ds = k.durations(1, [j, @mbt].min)
for d in ds do
i = j - d
for p in k.predecessors do
prob = γ[p, i]
∗ p.τ(k)
∗ k.δ(d)
∗ k.ε(x[i..j])
if (prob > γ[k, j]) then
γ[k, j], π[k, j] = prob, { p, d }
# Termination
best = γ[@end, x.len]
y = traceBack(x, γ, π)
return best, y, γx
j
d
i
k
p
γ[p][i]
ε(x[i..j])
δ(d)
τ(p)

Iterate until finding the best labeling sequence
Memory: \( O(SL) \)
Time: \( O(LSBC) \)
B
x[i..j]
HMM with non-geometric duration
GHMM's Viterbi
S
L
L
S
L
C
def PHMM::viterbi(xs)
# Initialization
γ = NArray.zeros(@states.len, xs[0].len, xs[1].len)
γ[@begin, 0, 0] = 1
# Iteration
for js in 1..xs[0].len, 1..xs[1].len do
for k in @states do
is = []
is.push(js[0] - k.Δ(0))
is.push(js[1] - k.Δ(1))
es = []
es.push(xs[0][is[0]]) if k.emits?(0)
es.push(xs[1][is[1]]) if k.emits?(1)
for p in k.predecessors do
prob = γ[p, *is]
∗ p.τ(k)
∗ k.ε(*es)
if (prob > γ[k, *js]) then
γ[k, *js], π[k, *js] = prob, p
# Termination
best = γ[@end, xs[0].len, xs[1].len]
y = traceBack(xs, γ, π)
return best, y, γL²
S
L
C
L
x₀
j₀
i₀
k
p
γ[p, i₀, i₁]
ε(x₀[i₀..j₀], x₁[i₁..j₁])
τ(p)
Memory: \( O(SL²) \)
Time: \( O(L²SC) \)
x₁
j₁
i₁
ε(x₀[i₀..j₀], x₀[i₁..j₁])
γ[p, i₀, i₁]
x₀[i₀..j₀]
x₁[i₁..j₁]

Iterate until finding the best labeling sequence
HMM extension for sequence alignment
PHMM's Viterbi
S
L
def GPHMM::viterbi(xs)
# Initialization
γ = NArray.zeros(@states.len, xs[0].length, xs[1].len)
γ[@begin, 0, 0] = 1
# Iteration
for js in 1..xs[0].len, 1..xs[1].len do
for k in @states do
dss = []
dss.push(k.ds[0](1, [js[0], @max_bt].min)))
dss.push(k.ds[1](1, [js[1], @max_bt].min)))
for ds in Array.product(*dss) do
is = []
is.push(js[0] - ds[0] * k.Δ(0))
is.push(js[1] - ds[1] * k.Δ(1))
es = []
es.push(xs[0][is[0]..js[0]]) if k.emits?(0)
es.push(xs[1][is[1]..js[1]]) if k.emits?(1)
for p in k.predecessors do
prob = γ[p, *is]
∗ p.τ(k)
∗ k.δs(*ds)
∗ k.εs(*es)
if (prob > γ[k, *js]) then
γ[k, *js], π[k, *js] = prob, { p, d }
# Termination
best = γ[@end, xs[0].len, xs[1].len]
y = traceBack(xs, γ, π)
return best, y, γL²
S
L
C
Memory: \( O(SL²) \)
Time: \( O(L²SB²C) \)
x₀
j₀
i₀
k
p
γ[p, i₀, i₁]
ε(x₀[i₀..j₀], x₁[i₁..j₁])
τ(p)
x₁
j₁
i₁
ε(x₀[i₀..j₀], x₁[i₁..j₁])
γ[p, i₀, i₁]
d₀
d₁
δ(d₀)
δ(d₁)
x₀[i₀..j₀]
x₁[i₁..j₁]
B²

Iterate until finding the best labeling sequence
PHMM with non-geometric duration
GPHMM's Viterbi
L
S
L
def GMHMM::viterbi(xs)
# Initialization
γ = NArray.zeros(@states.len, *xs.map(|x| x.len))
γ[@begin, *xs.map(|x| 0)] = 1
# Iteration
for js in *xs.map(|x| 1..x.len) do
for k in @states do
dss = k.ds.zip(js)
.each_with_index.reduce([])
{|pd,j,z| pd(1, [j, @mbt].min) if k.emits?(z)}
for ds in Array.product(*dss) do
is = js.zip(ds)
.each_with_index.map
{ |j,d,idx| j - d * k.Δ(idx) }
es = xs.zip(is).zip(js)
.each_with_index.reduce([])
{ |x,i,j,idx| x[i..j] if k.emits?(idx) }
for p in k.predecessors do
prob = γ[p, *is]
∗ p.τ(k)
∗ k.δs(*ds)
∗ k.εs(*es)
if (prob > γ[k, *js]) then
γ[k, *js], π[k, *js] = prob, { p, ds }
# Termination
best = γ[@end, *xs.map(|x| x.len)]
y = traceBack(xs, γ, π)
return best, y, γLᴺ
Lᴺ
S
Lᴺ
C

Iterate until finding the best labeling sequence
Memory: \( O(SLᴺ) \)
Time: \( O(LᴺSBᴺC) \)
x₀
j₀
i₀
k
p
γ[p, i₀, i₁]
ε(x₀[i₀..j₀], x₁[i₁..j₁])
τ(p)
x₁
j₁
i₁
ε(x₀[i₀..j₀], x₁[i₁..j₁])
γ[p, i₀, i₁]
d₀
d₁
δ(d₀)
δ(d₁)
x₀[i₀..j₀]
x₁[i₁..j₁]
Bᴺ
GPHMM for multiple sequences
GMHMM's Viterbi
S
def CM::cyk(x)
# Initialization
γ = NArray.zeros(@states.len, x.len, x.len)
(1..x.len).each { |j| γ[@begin, j, j] = 1 }
# Iteration
for j, i in 1..x.len, j..2 do
for k in @states do
l, r = i + k.Δ(:L), j - k.Δ(:R)
if not k.bifurcation? then
for child in k.children do
curr = γ[child, l, r] * p.τ(k.child)
prob = [curr, prob].max
else
for cut in (l..r) do
curr = γ[k.left, l, cut] * p.τ(k.left)
∗ γ[k.right, cut, r] ∗ p.τ(k.right)
prob = [curr, prob].max
prob *= k.ε(x[i..l], x[r..j])
if (prob > γ[k, i, j]) then
γ[k, i, j], π[k, j, j] = prob, p
# Termination
best = γ[@end, 0, x.len]
y = traceBack(x, γ, π)
return best, y, γS
L
L²
S
L
L
i
j
l
r
k
c₁
x
x[i..l]
x[r..j]
c₂
q
x[l..q]
x[q ..r]
τ(c₂)
τ(c₁)
γ[c₁, l, q]
γ[c₂, q, r]
ε(x[i..l], x[r..j])
Memory: \( O(SL²) \)
Time: \( O(L^2S_1C+L^2S_2L) \)
c
γ[c, l, r]
τ(c)
S₁
S₂
C
L
Iterate until finding the best labeling tree

#1: Start, End, Left, Right, Pairwise, Delete
#2: Bifurcation
Depending on the type of state:
Depending on the type of state:
Basic context-free model for labeling
CM's CYK
def GCM::cyk(x)
# Initialization
γ = NArray.zeros(@states.len, x.len, x.len)
(0..x.length).each { |j| γ[@begin, j, j] = 1 }
# Iteration
for j, i in 1..x.length, j..2 do
for k in @states do
dss = {}
dss[:L] = k.ds[:L](1, [j-i+1, @mbt].min)))
dss[:R] = k.ds[:R](1, [j-i+1, @mbt].min)))
for ds in *dss do
l, r = i + ds[:L]*k.Δ(:L), j - ds[:R]*k.Δ(:R)
if not k.bifurcation? then
for child in k.children do
curr = γ[child, l, r] ∗ p.τ(k.child)
prob = [curr, prob].max
else
for cut in (l..r) do
prod = γ[k.left, l, cut] * p.τ(k.left)
∗ γ[k.right, cut, r] ∗ p.τ(k.right)
prob = [curr, prob].max
prob *= δ(*ds) * k.ε(x[i..l], x[r..j])
if (prob > γ[k, i, j]) then
γ[k, i, j], π[k, i, j] = prob, { p, d }
# Termination
best = γ[@end, 0, x.len]
y = traceBack(x, γ, π)
return best, y, γi
j
l
r
k
c₁
x
x[i..l]
x[r..j]
c₂
q
x[l..q]
x[q ..r]
τ(c₂)
τ(c₁)
γ[c₁, l, q]
γ[c₂, q, r]
ε(x[i..l], x[r..j])
Memory: \( O(SL²) \)
Time: \( O(L^2S_1CB+L^2S_2L) \)
c
γ[c, l, r]
τ(c)
Iterate until finding the best labeling tree

#1: Start, End, Left, Right, Pairwise, Delete
#2: Bifurcation
Depending on the type of state:
Depending on the type of state:
d₁
d₂
δ(d₁)
δ(d₂)
CM with non-geometric duration
GCM's CYK
S
L
L²
S
L
L
S₁
S₂
C
L
B
Banca
está em
Avaliação