Ivan Lo

Repkironca

AaW

BrineTW

大社賽題解

大家寫的如何w

先來公佈名次摟

名次公佈

第二名 （6位)

300 分

  • YK
  • 准哥
  • 晴☆
  • 黑黑
  • 海之音
  • UN 

第一名

小蔡

320 分

特別獎

首刷

首AC

壓線submit (13:49:42)

  • Vic133
  • ckhs

pA.

同學我喜歡你

# 本場最難

Setter: 田鼠

就　　

　輸出

#include <iostream>
int main(){
    std::cout << "同學我喜歡你，我想整天near by you\n";
    return 0;
}

官解

吃WA數量比想像中多?

學校電腦某幾台似乎codeblocks

中文檔案會出錯

大家在submit時應該用複製貼上的比較好

pB.

解決問題的最佳方式

# 整數性質

# 模運算

# 閱讀理解

Setter: Repkironca

pB.

解決問題的最佳方式

總共有 N 筆詢問，每筆詢問包含一個數字\(q_i\)

若 \(q_i\) 是六位數，且 \(q_i\) 的前三位數 \(\leq\) 後三位數，輸出 No

否則輸出 Yes

  • 首先，你要看懂題目，因為這是閱讀理解
  • 接下來，我們要判斷，它丟給我的到底是不是六位數
  • 最後，我們要判斷，前三位數與後三位數的的關係

pB.

解決問題的最佳方式

總共有 N 筆詢問，每筆詢問包含一個數字\(q_i\)

若 \(q_i\) 是六位數，且 \(q_i\) 的前三位數 \(\leq\) 後三位數，輸出 No

否則輸出 Yes

  • 接下來，我們要判斷，它丟給我的到底是不是六位數
bool judge (int num){
  if (num < 100000 || num > 999999) return false;
}

pB.

解決問題的最佳方式

總共有 N 筆詢問，每筆詢問包含一個數字\(q_i\)

若 \(q_i\) 是六位數，且 \(q_i\) 的前三位數 \(\leq\) 後三位數，輸出 No

否則輸出 Yes

  • 把數字分離？

\ \(10^n\) 形同 刪除數字的後 n 位數

e.g. 78763 / \(10^2\) = 787

% \(10^n\) 形同 擷取數字的後 n 位數

e.g. 78763 % \(10^2\) = 63

pB.

解決問題的最佳方式

總共有 N 筆詢問，每筆詢問包含一個數字\(q_i\)

若 \(q_i\) 是六位數，且 \(q_i\) 的前三位數 \(\leq\) 後三位數，輸出 No

否則輸出 Yes

bool judge (int num){
  if (num < 100000 || num > 999999) return false;
  int l = num / 1000;
  int r = num % 1000;
  if (l <= r) return false;
  return true;
}

判斷實作

pB.

解決問題的最佳方式

官方解

#include <bits/stdc++.h>
#define icisc ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
using namespace std;

bool judge (int num){
  if (num < 100000 || num > 999999) return false;
  int l = num / 1000;
  int r = num % 1000;
  if (l <= r) return false;
  return true;
}

void solve (){
  int N; cin >> N;
  while (N--){
    int num; cin >> num;
    if (judge(num)) cout << "Yes\n";
    else cout << "No\n";
  }
}

int main (){
  icisc
  solve();
}

pB.

解決問題的最佳方式

神奇字串解　by. 准哥

#include<iostream>
#include<string>
#include<bits/stdc++.h>
using namespace std;
int main(){
    ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    string s;
    int n;
    cin >> n;
    for( int t = 0 ; t < n ; t++ ){
        cin >> s;
        if(s.length() != 6) {
            cout << "No" << endl;
        }
        else{
 
 
            if(s[0] > s[3]){
                cout << "Yes\n";
            }
            else if(s[0] == s[3]){
 
                if(s[1] > s[4]){
                    cout << "Yes\n";
                }
                else if(s[1] == s[4]){
 
                    if(s[2] > s[5]){
                        cout << "Yes\n" ;
                    }
                    else{
                        cout << "No\n";
                    }
                }
                else{
                    cout << "No\n";
                }
            }
            else{
                cout << "No\n";
            }
 
        }
 
    }
 
    return 0;
}

pC.

打扁鹽亞倫

# 陣列操作

# swap

# 真人真事改編

Setter: 鹽亞倫

Idea: 乘一

pC.

打扁鹽亞倫 

  • 這題是標準的操作題，要想辦法看懂題目希望你做的操作，並且準確地完成
  • 在處理陣列操作時，要看好index的處理

給你一個長度為\(n\) 的陣列 \(a[0] \, ... \, a[i] \, ... \, a[{n-1}]\) ，並且要你進行 \(m\)次操作。每次操作會給兩個位置\(i, j\)，要將\(a[i]\)和\(a[j]\)互換。最後，會問你\(q\)次問題，每一次給你一個\(k\)，問陣列中第\(k\)項的值是多少。

  • 這題的編號統一是 0-based，也就是任何時間編號都是\( 0 \sim (n-1)\)

pC.

打扁鹽亞倫 

給你一個長度為\(n\) 的陣列 \(a[0] \, ... \, a[i] \, ... \, a[{n-1}]\) ，並且要你進行 \(m\)次操作。每次操作會給兩個位置\(i, j\)，要將\(a[i]\)和\(a[j]\)互換。最後，會問你\(q\)次問題，每一次給你一個\(k\)，問陣列中第\(k\)項的值是多少。

  • 注意陣列要開多大，或是使用vector
  • 太大的陣列 (例如\(5 \times 10^6\))要開在全域變數

官解

陣列版

#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define endl '\n'
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);

signed main(){_
    int n, m ,q, a, b, k;
    cin >> n >> m >> q;
    ll arr[1000005] = {0};
    for (int i = 0; i < n; ++i) {
        cin >> arr[i];
    }
    for (int i = 0; i < m; ++i) {
        cin >> a >> b;
        ll temp = arr[a]; // 互換
        arr[a] = arr[b];
        arr[b] = temp;
    }
    for (int i = 0; i < q; ++i) {
        cin >> k;
        cout << arr[k] << '\n';
    }

    return 0;
}

官解

Vector版

#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define _ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);

signed main(){_
	vector<ll> v;
	int n, m ,q;
	cin >> n >> m >> q;
	for (int i = 0; i < n; ++i) {
		int a;
		cin >> a;
		v.push_back(a);
	}
	for (int i = 0; i < m; ++i) {
		int a, b;
		cin >> a >> b;
		swap(v[a], v[b]);
	}
	for (int i = 0; i < q; ++i) {
		int k;
		cin >> k;
		cout << v[k] << '\n';
	}
	return 0;
}

鞭屍

submit ID 185417201 by mhy1031

#include <bits/stdc++.h>
using namespace std;

int main(){
	int N,M,Q,count,i,j,ans;
	vector <int> a;
	while(N--){
		cin >> count;
		a.push_back(count); 
	}	
	while(M--){
		cin >> i >> j;
		swap(a[i],a[j]);
	}
	while(Q--){
		cin >> ans;
		cout << a[ans];
	}
	return 0;
}

再不加換行啊

鞭屍

submit ID 185416911 by 乘一

using namespace std;
#include <iostream>

int main(){
	ios_base::sync_with_stdio(false);
	cin.tie(0);
	int n,m,q;
	cin>>n>>m>>q;
	int arr[n];
	for(int i=0;i<n;i++){
		cin>>arr[i];
	}
	for(int i=0;i<m;i++){
		int a,b,temp;
		cin>>a>>b;
		temp = arr[a-1];
		arr[a-1] = arr[b-1];
		arr[b-1] = temp;
	}
	for(int i=0;i<q;i++){
		int num;
		cin>>num;
		cout<<arr[num-1]<<"\n";
	}
	return 0;
}

我都已經好心全部

0-based了誒

別以為你是出題者我就不會鞭你

鞭屍

submit ID 185416012 by star_huey

就說不要用怪怪編譯器了吧

pD.

嗯嗯嗯 + 1 問題

# 3n + 1 問題

# 模運算

# 遞迴或是迴圈的實作

Setter: 鹽亞倫

pD.

嗯嗯嗯 + 1 問題

進行t次以下動作：給你一個數字\(n\)，要你進行一個函數操作，問你要經過幾次操作之後函數值才會變成 1。

函數：

f(n) =  \left\{\begin{matrix} (1329\,n)\%2657 & \text{if } n \in \text{偶數} \\ (3n+1)\%2657 & \text{if } n \in \text{奇數} \end{matrix}\right.
  • 這題基本上是遞迴裸題，直接寫出來遞迴式就可以了
  • 但是到底什麼時候會無限？
  • 如果 A -> B -> C之後，C又->A，就會卡在這個輪迴中出不來！
  • 記錄每個數字有沒有出現過！

pD.

嗯嗯嗯 + 1 問題

雖然說是遞迴題，不過其實用迴圈的方式比較好寫

#include <bits/stdc++.h>
using namespace std;

const int mod = 2657;

signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        
        int cnt = 0;
        bool is_forever = false;
        vector<bool> visited(3000, 0);
        while (n != 1) {
            if (visited[n]) {
                is_forever = 1;
                break;
            }
            
            visited[n] = 1;
            if (n % 2) n = (3 * n + 1)%mod;
            else n = 1329 * n % mod;
            cnt++;
        }
        
        if (is_forever) cout << "forever\n";
        else cout << cnt << "\n";
    }
    return 0;
}

pD.

嗯嗯嗯 + 1 問題

用遞迴的官解

#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;

const int mod = 2657;
int cnt; // 答案
int visited[3000] = {0};
bool is_forever = false; 

void fun(int FBI) {
    if (FBI == 1) return;
    if (visited[FBI]) {
        is_forever = 1;
        return;
    }
    visited[FBI] = true;
    if (FBI & 1) FBI = (3*FBI + 1) % mod;
    else FBI = FBI * 1329 % mod;
    cnt++;
    fun(FBI);
}

signed main(){
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);

    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;

        cnt = 0;
        is_forever = false;

        fill(visited, visited+3000, 0);

        fun(n); // 開始遞迴

        if (is_forever) cout << "is_forever\n";
        else cout << cnt << "\n";
    }

    return 0;
}

pD.

嗯嗯嗯 + 1 問題

另一種解題的思維 by 陳皓樂大電神：

當已經遞迴超過2657次，一定是forever

因為答案不可能超過2657 -> 鴿籠原理

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int next(int c){
	if(c%2) return (3*c+1)%2657;
	else return (c*1329)%2657;
}


int main(){
	ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int t;cin>>t;
	while(t--){
		int a;cin>>a;
		int cnt=0;
		bool k = 0;
		while(a!=1){
			a= next(a);
			cnt++;
			if(cnt>2657){
			  k=1;	
			  break;
			}
		}
		if(!k) cout<<cnt<<"\n";
		else cout<<"forever\n";
	}
	return 0;
}

註：他用迴圈寫

pE.

老師我要把題目出得很難很難來教訓你們喔！

 

#我看起來有義務教會你嗎

Setter: Brine

〞

「我覺得這個模板他媽的超醜。」

—不是 BrineTW

我這次物理段考不及格啦幹

自己想

物理

話說有關AaW上課被臭的事情是真的

\(n_1\sin\theta_1 = n_2\sin\theta_2\)

Snell's Law

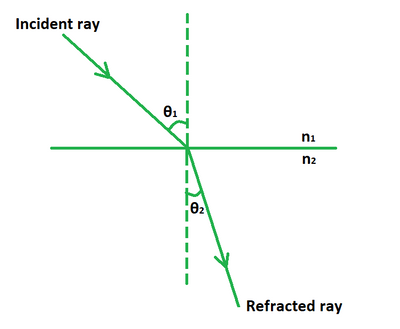
critical angle \(\theta_c: n_1\sin\theta_c = n_2\sin 90^\circ\)

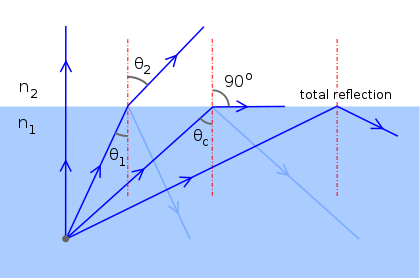
Total Internal Reflection

TIR happens when \(\theta \ge \theta_c\)

\(\because |\sin\theta| \le 1\)

\(\therefore \exists \theta_c \leftrightarrow \frac{n_2}{n_1} \le 1\)

Title

n_1\sin\theta_1 = n_2\sin\theta_2 = n_3\sin\theta_3
n_1\sin\theta_1 = n_3\sin\theta_3?

what if \(\theta_1 > \theta_{c_{12}}?\)

n_1\sin\theta_1 = n_3\sin\theta_3 \leftrightarrow n_1\sin\theta_1 < n_2\sin 90^\circ

print \((i-1, i)\) whenever \(n_i < \displaystyle\min_{0\le j < i}n_j\)

solution

pF.

 

一個蛋解決的問題

 

Setter: 溫敬和的狗

圍網無法推行主要因素

圍網不通風

雞的毛、灰塵等物堵塞圍網導致圍網產生通風問題，進而造成雞隻的健康問題。

1.

圍網影響人及野鳥動線

在雞場走動及清理時常常會因圍網而影響動線，野鳥也無法進來吃蟲，維持平衡，現今反而因蛆過多導致衛生問題。

2.

損毀問題及修繕成本

加裝後若因颱風等問題導致圍網損毀可能因維護不符合生產效益而不再使用，或產生過大成本。

3.

因地制宜問題

每個雞場需求不同，須因地制宜，蛋修改後方案可能因此失效。

4.

法規本身對於雞農修正的動機不足

法規當中的各項補助或類懲罰機制不足以使雞農對現有技術物及養殖方式進行調整。

5.

小結