運算思維之雜七雜八

你沒看錯，第一堂課就直接想不到命名

Lecturer：Repkironca、Rainple

  • 學校不教的酷東西

可能的收穫

些許副作用

  • 教你數學的人數學很爛
  • 對高一數學有點印象
  • 讓 Aaw 的課變比較好懂
  • 不被 108 課綱搞到
  • 講師可能很小丑
  • 要用到時已經忘記了
常見數學符號 進位制 位元運算
邏輯敘述 集合 數據分析
三角函數 排列組合 向量與矩陣
基礎數論 基礎微積分 怪怪的技巧
  • 有點程式又不太程式

IG 推坑時間

- ㄟ你知道要怎麼假文青ㄇ

追蹤一些看起來很厲害的專頁！

（看不懂就算了，反正做做效果）

沒什麼特別的，就是沒營養的東西

枯嶺街學測戰士\\@ peng.hc

JEE 導向，針對理科的一些公式、定理等

偶而摻雜甚至是迷因之類的，比較符合高中程度

IIT-JEE\;GAMING\\@iitjeegaming

JEE 導向，每天掉落一個進階題目，隔天附上解答，然後字體很美

Mathematics\\@moiitjee

一大堆酷公式、定理，外加證明

Curious Mind\\@curious\_math

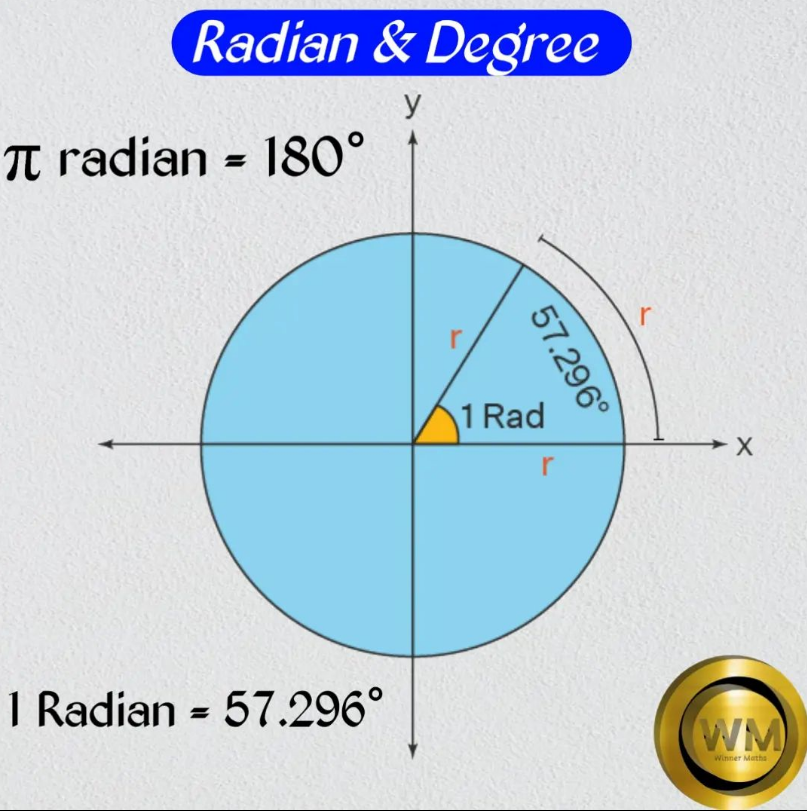
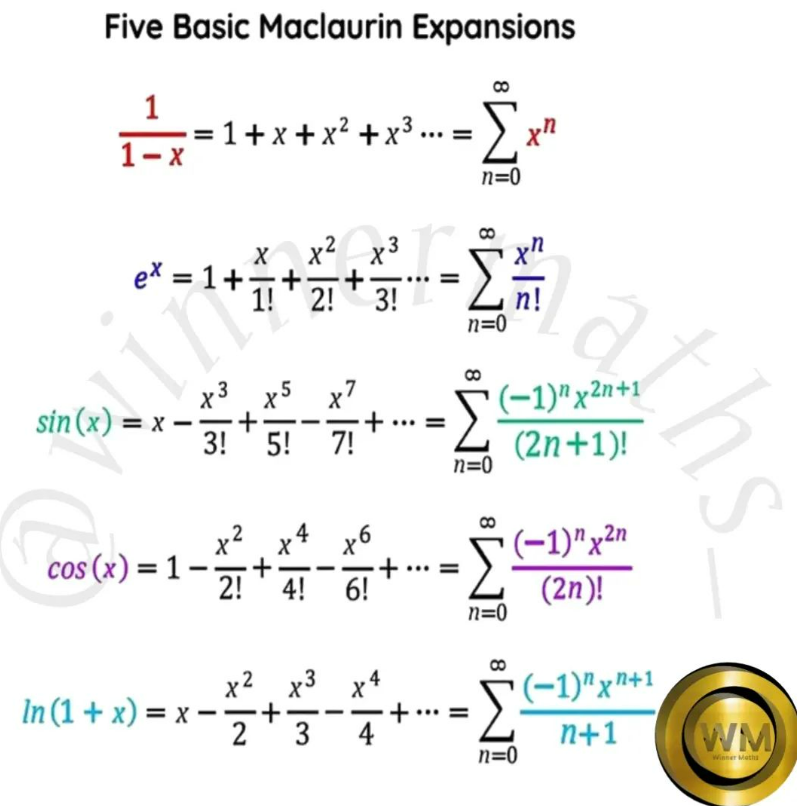
把數學原理、公式等東西，用圖像化表達

很多都是高中程度的東東，相對基礎不少

Chandan\;Kumar\\@winnermaths\_

一點點希臘字母

你要更多資訊的話可以點進來

\Alpha/ \alpha

alpha

－與 A 相對的符號\\通常用在\triangle中

－會搞混，沒什麼鳥用

\Beta / \beta

beta

－與 B 相對的符號\\通常用在\triangle中

－你目前不會用到大寫

\Gamma / \gamma

gamma

－與 C 相對的符號\\通常用在\triangle中

－函數名，表階乘

\Mu / \mu

Mu

－物理上的質量因次

－平均值、莫比烏斯函數

\Theta / \theta

theta

－物理上的溫度因次

－角度，超級常被使用

\Delta / \delta

delta

－變數的變化量

－COVID - 19 的變種

\Pi / \pi

pi

－連乘符號

－圓周率

\Sigma / \sigma

sigma

－連加符號

－母體標準差

\Omega / \omega

omega

－電阻單位、時間複雜度函數

－角速度

108 課綱就不能

把數系教完整嗎

＂理論上＂你們已經學會的

仙貝姿勢

＂外加＂被 108 課綱黑掉的東西

數系 Number System

Beyond Complex Numbers？

自己看，因為我也看不懂：）

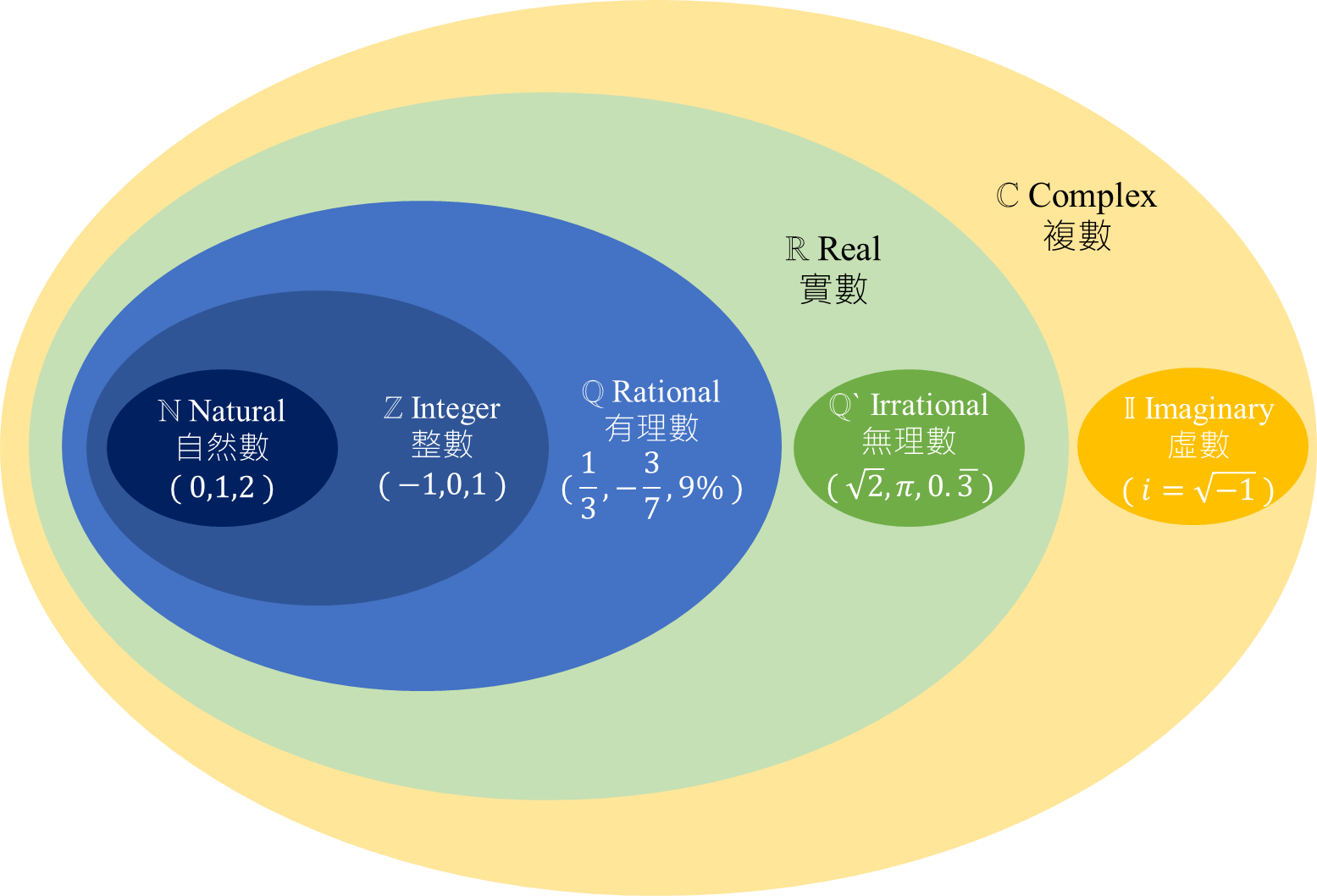
虛數 Imaginary Numbers

－對，你們聽過的虛數符號

i
定義\;i\,^2\;=\;-1
How\;about\;i\;=\;\sqrt{-1}？

合理，但盡量不要使用

\sqrt{a}\;×\sqrt{b}\;=\;\sqrt{ab}，\forall\;a、b > 0
(X) i\;×\;i\;=\;\sqrt{-1}×\sqrt{-1}\;=\;\sqrt{1}
\sqrt{a}\;×\sqrt{b}\;=\;-\sqrt{ab}，\forall\;a、b\;<\;0

計算太複雜了，而且一堆例外，好煩

i\,^0\; = \;1，單純按照\;0\;次方的定義

虛數 Imaginary Numbers

i\,^1\; = \;i，嗯，廢話：）
i\,^2\; = \;-1，虛數\;i\;的基本定義
i\,^3\; = \;i^2\;×\;i \;= \;(-1)×\;i \;= \;-\,i
i\,^4\; = \;i^2\;×\;i^2 \;= \;(-1)×\;(-1) \;= \;1
刷成就感的水題：求\;i\,^0\;+\;i\,^1\;+\;i\,^2\;+\;...\;+i\,^{997} \;之值
Ans：1 + i

複數 Complex Numbers

-\;Ans：1 + i，實數加虛數？
定義\;：\;a\;+\;b\,i

實部

虛部

-\;共軛複數：實部相等，b 互為相反數
5\;+\;7\,i
5\;-\;7\,i
13\;+\;17\,i
13\;-\;17\,i
x\;=\;a\;+\;b\,i
\overline{x}\;=\;a\;-\;b\,i
if\;b\;=\;0\;\wedge\;a\;\in\;R，then\;(\,a\;+\;b\,i\,)\;\in\;R
if\;b\;\neq\;0\;\wedge\;a、b\;\in\;R，then\;(\,a\;+\;b\,i\,)\;\in\;I

複數 Complex Numbers

加法：\overline{x}\;+\;\overline{y}\;=\;\overline{x\;+\;y}
\overline{1\;+\;2\,i}\;+\;\overline{2\;-\;3\,i}
=\;1\;-\;2\,i\;+\;2\;+\;3\,i
=\;3\;+\;i\;=\;\overline{3\;-\;i}
乘法：\overline{x}\;×\;\overline{y}\;=\;\overline{x\,y}
\overline{1\;+\;2\,i}\;×\;\overline{2\;-\;3\,i}
=(\,1\;-\;2\,i\,)\;(\,2\;+\;3\,i\,)
=\;2\;+\;3\,i\;-\;4\,i\;-\;6\,i^2
=\;8\;-\;i\;=\;\overline{8\;+\;i}
試求\,x\,^2\;-4\,x\;+\;5\;之解？

＂蛤可是它的判別式小於 0 耶＂

x = \frac{4\;\pm\;\sqrt{-4}}{2}
\;= \frac{4\;\pm\;\sqrt{4}\,i}{2}
\;= 2\;\pm\;i
Ans\;\in\;I，且兩根互為共軛複數

SOURCE，有興趣可以慢慢點

因為我懶所以沒 APA，不良示範請勿模仿

  • 2-3A觀念03虛數i的介紹
  • 2-3A觀念04複數a+bi
  • 2-3A觀念05共軛複數與其性質
  • 2-3A觀念06一元二次方程式的判別式之討論
  • 2-3A觀念05共軛複數與其性質

常見的數學符號

用中文寫數學真的很慢.jpg

而且外國人看不懂

很多東西想用更正式的方法表達

卻不知道怎麼下手ㄇ

你需要的是 Google

我是說，你需要的是等等的課程！

!

階乘 Factorial

－白話定義：一直往下乘下去，直到 1 為止

－數學定義：n\,!\;=n\;×\;(\,n\;-\;1\,)\,!
4\,!\;=\;4\;×\;3\;×\;2\;×\;1\;=\;24
\because 1\,!\;=\;1\;×\;0\,!\;=\;1
\therefore define\;0\,!\;=\;1

如果你想知道，可以啃這篇論文

\frac{1}{2}\,!\;=\;\frac{\sqrt{\pi}}{2}

for more information

\forall\;n\;\in\;N
n= 0
\forall\,n\in R\wedge n \geq0
\forall\,n\in R

屬於 Belongs To

\in

不屬於 Not Belongs To

\notin

－字面上的意思，後面常接一個數系

\pi\;\in\;R
\sqrt{-7122}\;\notin\;R

對於所有 For All

\forall

－後面也可以接一個集合，等等會講到

－拜託不要講中文，沒人聽得懂

－同樣字面上的意思，代表 每個 case 都符合此條件

n\;\leq\;100，\forall\;n\;\in\;Z

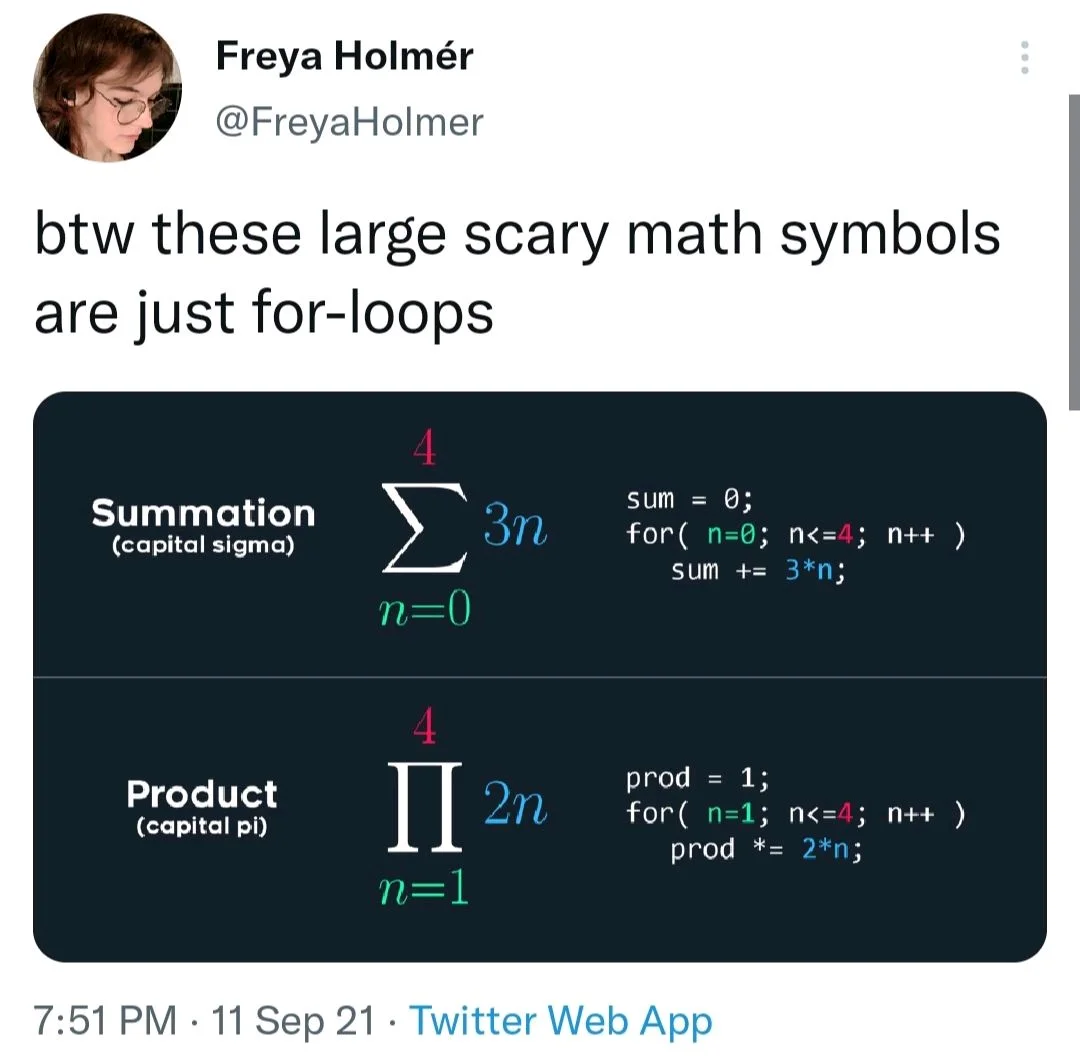
求和符號 Summation

\Sigma

－那個符號正是大寫 Sigma，我們也會這樣叫它

1, 2, 3, 4, 5, 6, 7, 8, 9, 10
\Sigma_{i = 1}^{10}\;i
1 + 2 + 3 + ... + 10 = 55
\Sigma_{i = 1}^{10}\;i\;=\;55

－一個計數器，每次遞增 1，再把結果加起來

i\;=\;1：計數器命名為\;i，從＂1＂開始往上遞增\;1
10：當計數器數完＂10＂後就會結束
i（右邊的）：把每個時刻的＂i＂都加起來

求和符號 Summation

\Sigma

一點點小變化？

\frac{\Sigma_{i = 1}^{n}\;(x_i＋y_i)}{2n}

每次各加一個 x 與 y 進來

最終總共有 2n 項！！

\Sigma_{i = 5}^{15}\;i
5＋6＋7＋...＋15
\Sigma_{i = 1}^{10}\;2\,i
(2×1)＋(2×2)＋...＋(2×10)
\Sigma_{i = 1}^{10}\;(2\,i + 3)
(2×1+3)＋(2×2+3)＋...＋(2×10+3)
\Sigma_{i = 1}^{10}\;4
4+4+4+4+4+4+4+4+4+4
\Sigma_{i = 1}^{n}\;x_i
x_1＋x_2＋x_3＋...＋x_n
x_1＋x_2＋x_3＋...＋x_n
y_1＋y_2＋y_3＋...＋y_n

求兩數列之平均？

求積符號 Product

\Pi

－跟求和符號一模一樣，只是 "加" 改成 "乘"

－那個就是大寫 Pi，但我不會這樣叫他

\Pi_{i = 1}^{10}\;i
1×2×3×...×10
\Pi_{i = 1}^{n}\;(2\,x_i)
2\,x_1×2\,x_2×2\,x_3×...2\,x_n
\Pi_{i = 2}^{20}\;(i(i－1))
(2×1)×(3×2)×...×(20×19)
\Pi_{i = 1}^{5}\;((x_i＋y_i)×(x_{2i}－y_{2i}))
[(x_1＋y_1)(x_2－y_2)]×[(x_2＋y_2)(x_4－y_4)]×...×[(x_5＋y_5)(x_{10}－y_{10})]

其實我本來想繼續教

但我怕這堂課會太＂充實＂

有興趣可以點進來繼續看

如果你有追前面推坑的 IG 會需要

換講師時間 :partying_face:

等等你會看到巨大的

簡報風格差距 XDD

 

然後請記住 無論他等等說了什麼

全都不代表本人立場

不要聽他唬爛==

邏輯

那是是非非都似是而非建立ㄉ基礎

會有一坨東西 但蠻少真的用到ㄉ

英文 中文 邏輯符號 C++ 邏輯運算子 意義
not 非 ¬ A / ~A ! A A的反相(布林反轉)
and 且 A ∧ B A && B AB皆T→T
or 或 A ∨ B A || B AB任一為T→T
xor 異或 A ⊕ B A ^ B AB僅一為T→T

基本邏輯符號&意義

．布林值：0/1 ( Ture / False )

．布林式：一坨布林值的運算式，結果是布林值

A B A ∧ B
T T T
T F F
F T F
F F F
A B A ∨ B
T T T
T F T
F T T
F F F
A B A ⊕ B
T T F
T F T
F T T
F F F

and（且）

or（或）

xor（異或）

真亦假假亦真真值表

Pop Quiz！

( ~ ( 0 ∨ ( ( 1 ⊕ 1 ) ∧ 1 ) ) ⊕ 0 ) ∧ 1 =True/False?

　( ~ ( ( 0 ∨ ( ( 1 ⊕ 1 ) ∧ 1 ) ) ⊕ 0 ) ) ∧ 1

⇒( ~ ( ( 0 ∨ ( 0 ∧ 1 ) ) ⊕ 0 ) ) ∧ 1

⇒( ~ ( ( 0 ∨ 0 ) ⊕ 0 ) ) ∧ 1

⇒( ~ ( 0 ⊕ 0 ) ) ∧ 1

⇒( ~ 0 ) ∧ 1

⇒1 ∧ 1

⇒1

¬ / ~ / not / 否定

「否定敘述即用最低代價使原敘述不成立之敘述」

(p.s. 否定敘述是相對ㄉ)(p.p.s.只在原敘述的範圍內更動)

So how to把肯定改成否定？

．直接把是改不是？

跟白癡一樣，白癡得要命。

1. 改成概念相反的述語（使不成立）

　「是、會、有」改「非、不、無」

　「大／小於」改「小／大於等於」

　單純「v.、n.、adj.」加「非、不」

2. 偏稱全稱互換（用最小代價）

　「都、皆、全」與「有」互換

　「和、並、且」與「或」互換

黑

↓

白

全班都及格

↓

全班不及格

是故，「至多10人數學及格」的否定敘述是

「超過10人數學及格」或「至少11人數學及格」

(2.只有特定情況要用)

(自然數範圍內的推理)

非黑

全班不及格

↓

有人不是及格

What is 「只在原敘述的範圍內更動」？

Ans：不要講太多，根本沒人在乎

e.g. ~ ( 蘇昱亙是白癡 ) ≡ 蘇昱亙不是白痴

或蘇昱亙是熱鯊

或蘇昱亙是

菸鹼醯胺腺嘌呤二核苷酸磷酸

或蘇昱亙是位能

或蘇昱亙是八元數

不用特別講，沒人在乎

超出我們討論的範圍

其他例子：~ ( x > 2 ) ≡  ( x ≤ 2 ) ∨ ( x ∉ ℝ)

　　　　　超過10人及格 ≡ 至少11人及格或人數不是自然數

\begin{cases} 　\\ 　\\ 　\\ 　\\ 　 \end{cases}

．充分必要條件 if

 若P則Q：P → Q（Ｐ成立時Ｑ必成立）

P是Q的充分(條件)

Q是P的必要(條件)

※否定後件

P → Q（Ｐ則Ｑ）

~Q→~P（非Ｑ則非Ｐ）

Ｑ ≥ Ｐ

跟蘇昱亙溝通 會 腦霧（P→Q）

不跟蘇昱亙溝通

（~P→♢Q）

不一定會 腦霧

腦霧

不一定 跟蘇昱亙溝通過

（Q→♢P）

不腦霧

一定 沒跟蘇昱亙溝通

（~Q→~P）

Ｐ發生

Ｑ亦發生

Ｑ發生

Ｐ不一定發生

．若且唯若 if and only if / iff

若Ｐ則Ｑ(Q if P)：Ｐ→Ｑ

唯若Ｐ則Ｑ(Q only if P)：¬Ｐ→¬Ｑ⇔Ｑ→Ｐ

若且唯若Ｐ則Ｑ(Q iff P)：

(Ｑ→Ｐ) ∧ (Ｐ→Ｑ) ⇔ (Ｐ⇔Ｑ)

Ｐ與Ｑ互為充分必要條件（充要條件）

即ＰＱ等價

＋

‖

=

Ｑ ≥ Ｐ

Ｐ ≥ Ｑ

Ｐ＝Ｑ

集合

Set

What is 集合？

Ans：由一坨元素構成的群體，通常用Ｓ(set)表示單個集合

e.g.一鍋火鍋是一個集合，蟹肉棒、烏龍麵、五花豬、昆布湯都是一種元素

怎麼表示有的元素？

\begin{aligned} S_1&=\{1,2,4,8,125\}\\ &\Rightarrow S_1裡面有(1),(2),(4),(8),(125)這五個元素\\ S_2&=\{3.14,\{1,2,3\},i,\pi\}\\ &\Rightarrow S_2裡面有(3.14),(有(1),(2),(3)的集合),(i),(\pi)這四個元素 \end{aligned}

列舉法

S={...}

描述法

S={...|...的描述}

\begin{aligned} S_3&=\{x|x\in\mathbb{R}\wedge x^2-7x+6\geq0\}\\ &\Rightarrow S_3內的每個元素x皆屬於實數並符合x^2-7x+6\geq0\\ S_4&=\{(x,y)|y=\sin x\wedge x\in\mathbb{R}\}\\ &\Rightarrow S_4內的每個元素數對(x,y)皆在方程式y=\sin x上 \end{aligned}

元素型式統一，具有某個特徵

元素量可能無限

不計次序，不計重複，不計屬性

元素性質不一，量通常少

．名詞符號解釋

舉個例子： S=\{1,2,3,4,5\}

1,2,3,4,5皆是元素，而屬於S

\begin{aligned} &\in 屬於\ Belongs\;to，[元素]\in[集合]\\ &e.g.\ 1\in S \end{aligned}

如果有一個集合T的元素皆屬於S，

此時稱T為S的子集，而T包含於S

\begin{aligned} &\subset/\subseteq 包含於\ Contained\;in，[子集]\subset[集合]\\ &e.g.\ T=\{1,2,3\},T\subset S \end{aligned}

有個集合啥都沒，則稱之為空集合，

記作 {} 或 ∅ ，且∅為任一集合之子集

\begin{aligned} &\varnothing\ 空集合\ Empty\;Set，\\ &e.g.\ \varnothing\subset S \end{aligned}

有個集合包含所有 S 的研究對象，

稱之為宇集或基集，記為 U

\begin{aligned} &\mathrm{U}\ 宇集/基集\ Universal\;Set，\\ &e.g.\ S\subset \mathrm{U} \end{aligned}

如果Ｓ是有限集合（元素量可數），

此時用 n(S) 或 |S| 表示Ｓ的元素量

\begin{aligned} &n(S)\ /\ |S|\ S的元素個數\ The\;number\ of\ S，\\ &e.g.\ n(S)=|n|=5 \end{aligned}

Pop Quiz！

S=\{\varnothing,1,2,\{3,4\},\{5\}\}
\begin{aligned} (　)\ 1.&\ 1\in S\\ (　)\ 2.&\ \{1,2\}\in S\\ (　)\ 3.&\ \{3,4\}\in S\\ (　)\ 4.&\ \{3\}\subset S\\ (　)\ 5.&\ 4\in S\\ \end{aligned}

Ｏ

Ｏ

Ｏ

Ｏ

╳

╳

╳

\begin{aligned} (　)&\ 6.\ \varnothing \in S\\ (　)&\ 7.\ \varnothing \subset S\\ (　)&\ 8.\ \{\{5\}\}\subset S\\ (　)&\ 9.\ 5\in S\\ (　)&\ 10.\ n(S)=6 \end{aligned}

╳

╳

Ｏ

Pop Quiz！

今有一個有限集合Ｓ，Ｓ共有多少不同子集？

令\forall A\subset S
\Rightarrow A的總數量=2^{n(S)}

每個子集，

對其中每個元素皆有拿(使屬於A)或不拿(使不屬於A)兩種選擇

每遇到一個元素就\times 2
Ans: 2^{n(S)}

．集合ㄉ計算

U

A

B

2.交集\cap :A\cap B=\{x|x\in A\wedge x\in B\}
1.聯集\cup :A\cup B=\{x|x\in A\vee x\in B\}
3.差集- :A - B=\{x|x\in A\wedge x\notin B\}
\begin{aligned} &4.補集'/\overline{　}:\\ &　B^{'}=\ \overline{B}=\{x|x\notin B \wedge x\in U\} \end{aligned}

．狄摩根定律

(A\cup B)^{'}=A^{'}\cap B^{'}
(A\cap B)^{'}=A^{'}\cup B^{'}

Pop Quiz！

若一班有40人，32人喜歡玩傳說對決，

24人喜歡玩神魔之塔，28人喜歡玩弓箭傳說。

請問同時喜歡三個遊戲的人(1)最多_____人(2)最少_____人

-建國中學 110學年度 下學期 第二次段考 數學科 第六題 我被隔離QAQ

. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .

24

. . . . . . . .
. . . . . . . .
. ​. ​. ​. ​. ​. . .





​. ​. ​. ​.


​. ​. ​. ​. ​. ​. ​. ​.
. . ​. ​. . . . ​.
. ​. ​. ​. ​. ​. . .

4

．補充：積集

\begin{cases} {\color{red}A=\{x|x\equiv 1 (mod\ 2)\}}\\ {\color{blue}B=\{y|y\equiv 1 (mod\ 3)\}} \end{cases}

０

1　　2　　3　　4　 　5　　6　 　7　　8　　9

9

8

7

6

5

4

3

2

1

(1,1)

(1,4)

(1,7)

(3,7)

(5,7)

(7,7)

(7,4)

(7,1)

(5,1)

(5,4)

(3,4)

(3,1)

A\times B=\{(x,y)|x\in A\wedge y\in B\}, n(A\times B)=n(A)\times n(B)

好大概就先這樣就好

集合最廣泛運用到會在排列組合

我們到時候再回來面對它ㄅ