Planning with Graphs

of Convex Sets

Russ Tedrake

Grasp Lab Seminar

October 29, 2021

Slides available live at https://slides.com/d/absz0Qc/live
or later at https://slides.com/russtedrake/2021-grasp

Shortest Paths in Graphs of Convex Sets

Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake. Shortest Paths in Graphs of Convex Sets. (Under review)

Available at: https://arxiv.org/abs/2101.11565

Shortest Paths on Graphs of Convex Sets

Sample-based motion planning

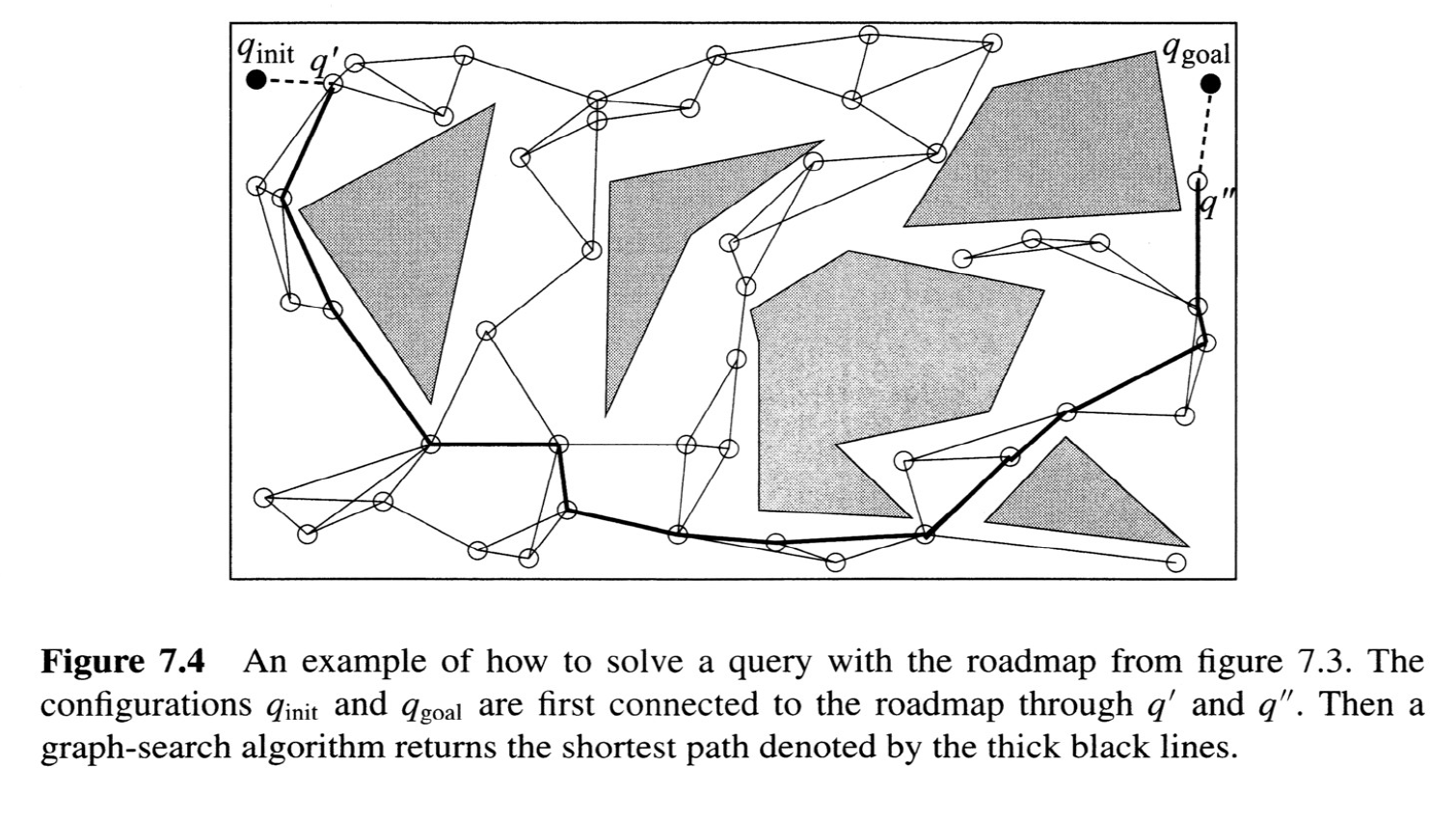
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.

Goal #1: Motion planning

Global optimization-based planning for manipulators with dynamic constraints

 

  • Planning through contact
  • Today: Collision-free planning

image credit: James Kuffner

Approximate

Goal #2: Deeper connections between

Trajectory optimization

Sample-based planning

AI-style logical planning

Combinatorial optimization

Collision-free planning with dynamic constraints

Running example: Shortest path around an obstacle

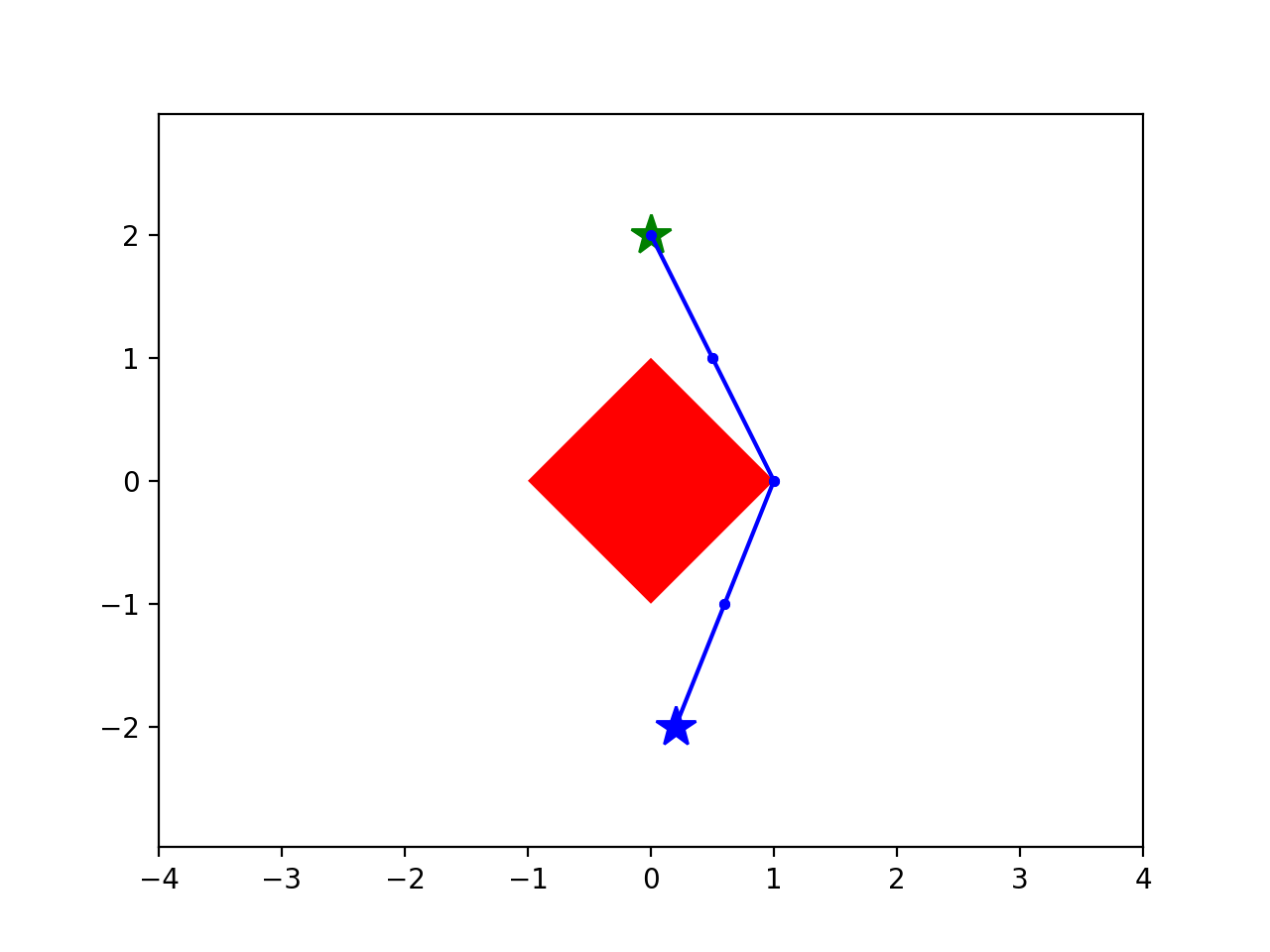
start

goal

Step 1:

Big-M formulation

IRIS (Fast approximate convex segmentation)

  • Iteration between (large-scale) quadratic program and (relatively compact) semi-definite program (SDP)
  • Scales to high dimensions, millions of obstacles
  • ... enough to work on raw sensor data

Running example: Shortest path around an obstacle

start

goal

Step 2:

Convex hull formulation

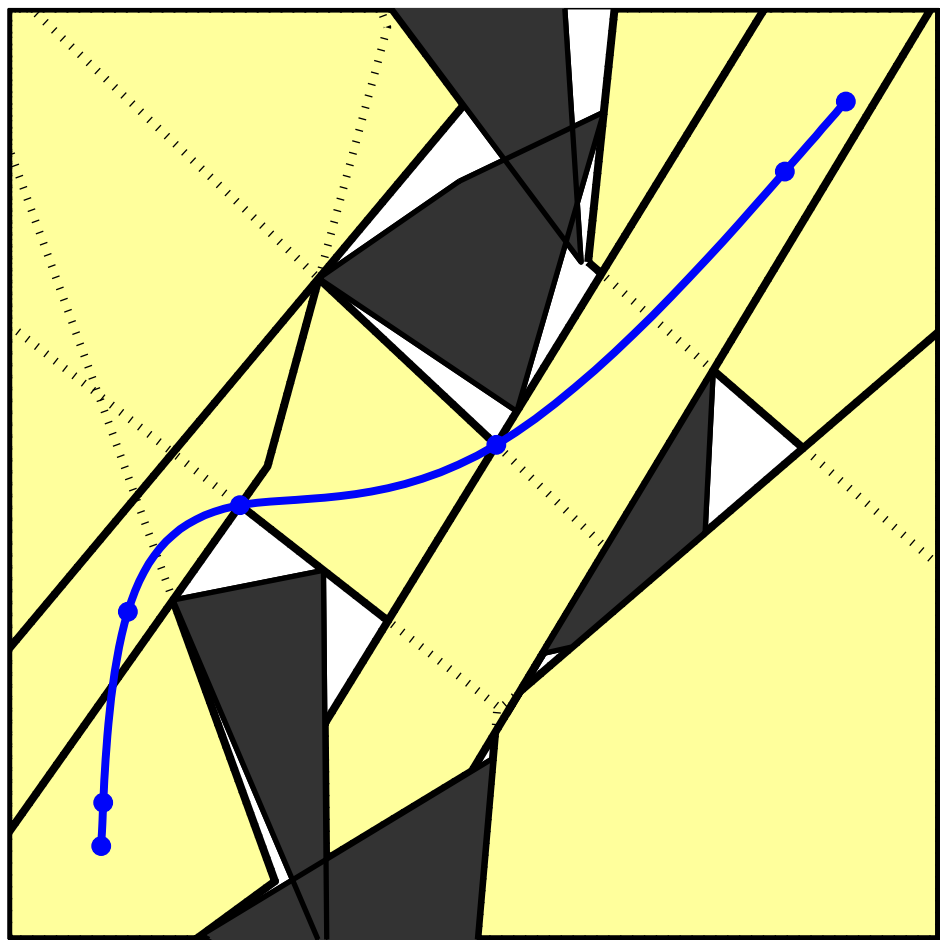
  • Guaranteed collision-free along piecewise polynomial trajectories
  • Complete/globally optimal within convex decomposition

Dynamic planning through contact

Dynamic planning through contact

Still not happy...

  • Too many integer variables
    • transcriptions add "false" combinatorial complexity

 

  • Branch and bound working too hard
    • loose convex relaxations

Pablo asked the right question...

"We know that the LP formulation of the shortest path problem is tight.  Why exactly are your relaxations loose?"

  • Vertices \(V\)
  • (Directed) edges \(E\)

Traditional Shortest Path as a Linear Program (LP)

\(\varphi_{ij} = 1\) if the edge \((i,j)\) in shortest path, otherwise \(\varphi_{ij} = 0.\)

\(c_{ij} \) is the (constant) length of edge \((i,j).\)

\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\ \mathrm{s.t.} \quad & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si}, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

"flow constraints"

binary relaxation

path length

Graphs of Convex Sets

 

  • For each \(i \in V:\)
    • Compact convex set \(X_i \subset \R^d\)
    • A point \(x_i \in X_i \) 
  • Edge length given by a convex function \[ \ell(x_i, x_j) \]

New shortest path formulation

\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\ \mathrm{s.t.} \quad & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si}, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

Classic shortest path LP

\begin{aligned} \min_{\varphi,x} \quad & \sum_{(i,j) \in E} \ell_{ij}(x_i, x_j) \varphi_{ij} \\ \mathrm{s.t.} \quad & x_i \in X_i, && \forall i \in V, \\ & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si} \le 1, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

now w/ Convex Sets

New shortest path formulation

\begin{aligned} \min_{\varphi,x} \quad & \sum_{(i,j) \in E} \ell_{ij}(x_i, x_j) \varphi_{ij} \\ \mathrm{s.t.} \quad & x_i \in X_i, && \forall i \in V, \\ & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si} \le 1, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}
  • Use convex hull reformulation + perspective functions to rewrite this as mixed-integer convex.
  • Strengthen convex relaxation by adding additional convex constraints (implied at binary feasibility).

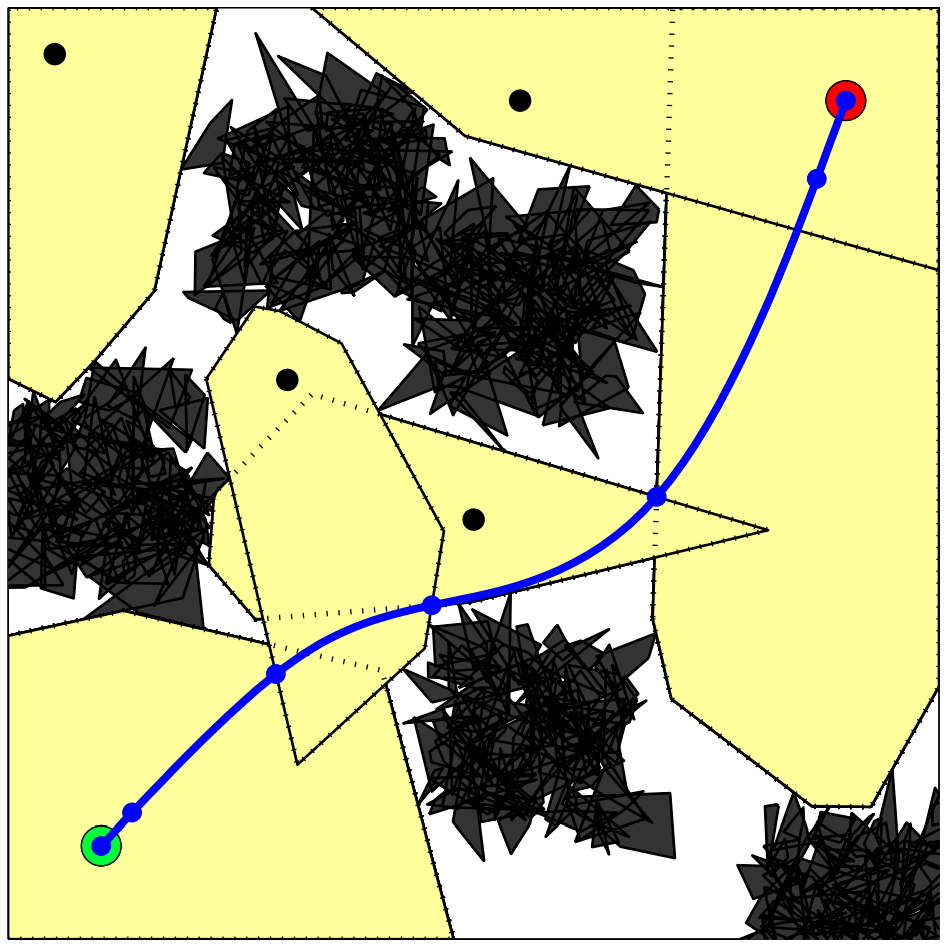
Running example: Shortest path around an obstacle

start

goal

Step 3:

New formulation

Did we resolve our issues?

  • Too many integer variables
    • transcriptions add "false" combinatorial complexity

 

  • Branch and bound working too hard
    • loose convex relaxations

Note: Path length is no longer predetermined

          is the convex relaxation.  (it's tight!)

Euclidean shortest path

  • Finding the shortest path from A to B while avoiding polygonal obstacles (“Euclidean shortest path”):
    • Solvable in polytime in 2D (with a visibility graph)
    • NP-hard from 3 dimensions on
    • For the 3D case there exists an approximation algorithm which gives you \(\epsilon\)-optimality in poly time
    • Nothing is known for dimension \(\ge 4\)

 

  • New formulation:
    • Provides polynomial-time algorithm for dimension \(\ge 4\) that is often tight.
    • Solves a more general class of problems (e.g. can add dynamic constraints).
  • When sets \( X_i \) are points, reduces to standard LP formulation of the shortest path (known to be tight).

 

  • There are instances of this problem that are NP-hard.
  • We give simple examples where relaxation is not tight.

​

  • Can add (piecewise-affine) dynamic constraints on pairs \( (x_i,x_j). \)

Remarks

Example: "Footstep planning" with \(x_{n+1}=Ax_n + Bu_n\)

Previous best formulations New formulation
Lower Bound
(from convex relaxation)		 7% of MICP 80% of MICP

Scaling

Most important changes (vs previous formulation)

  1. Binaries per edge, instead of per region
  2. Additional constraints which tighten the convex relaxation

Should be suitable for many graph-based optimization problems

Going forward...

Example: Bipartite matching (with convex regions)

Back to motion planning

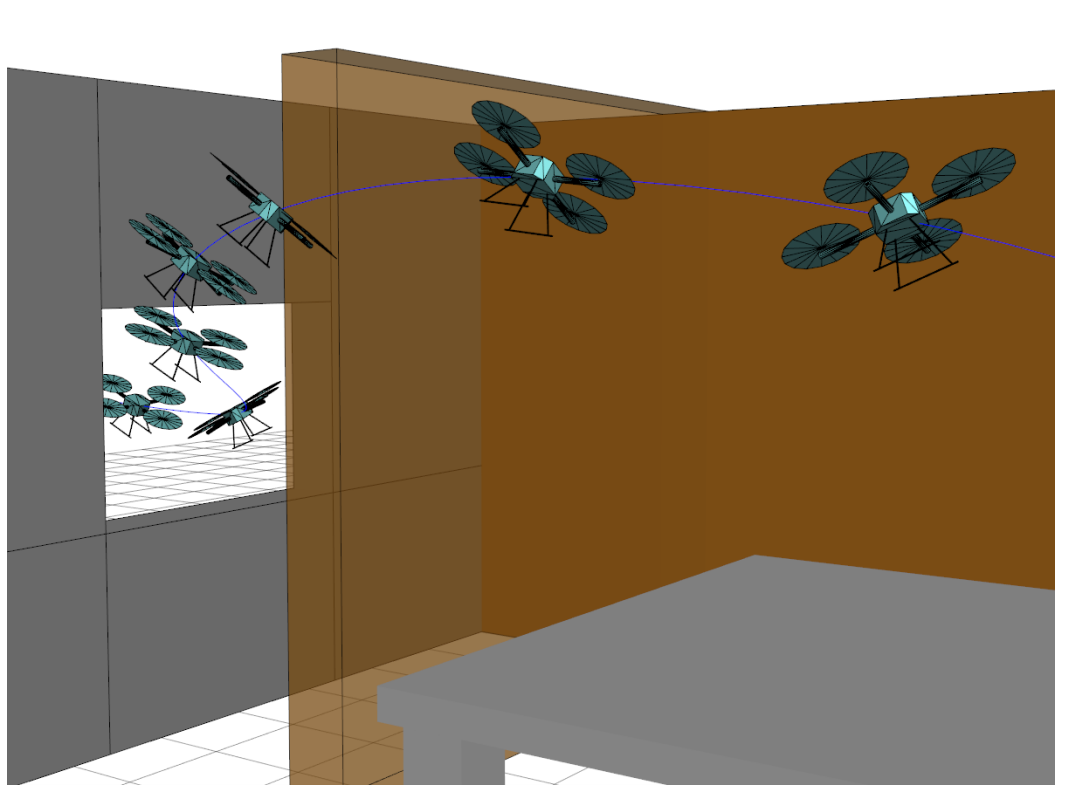
Manipulators at the dynamic limits

  • Real applications are bumping up against dynamic limits (joint speed/acceleration/torque and friction limits, etc)
  • Observation: diverse motions, but relatively consistent environment.
    • Precompute regions to make online optimization fast

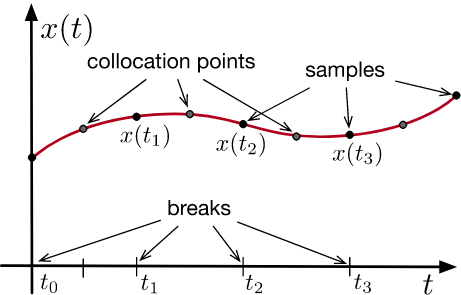
Trajectories in graphs of convex sets

  • B-spline parameterization
  • Convex sets are Cartesian power of C-space regions

 

  • Linear constraints connect segments
  • Linear constraints for derivative limits (joint velocity, acceleration, ...)

work w/ Andres Valenzuela

Configuration-space regions

  • Original IRIS algorithm assumed obstacles were convex
  • New extensions for C-space
    • Nonlinear optimization for speed
    • Interval arithmetic for verification

work w/ Soonho Kong

Time-optimal rescaling

work w/ Mark Petersen

drake.mit.edu

"Hydroelastic contact" as implemented in Drake

Summary

  • New strong mixed-integer convex formulation for shortest path problems over convex regions
    • reduces to shortest path as regions become points
    • NP-hard; but strong formulation \(\Rightarrow\) efficient B&B
    • Convex relaxations are often tight!  \(\Rightarrow\) Rounding strategies
  • Initial applications in manipulator planning at dynamic limits

 

Give it a try:

pip install drake
sudo apt install drake

drake.mit.edu

Goal #2: Deeper connections between

Trajectory optimization

Sample-based planning

AI-style logical planning

Combinatorial optimization

My MIT manipulation class is online (videos + notes)

http://manipulation.mit.edu