Certified motion planning around obstacles with convex optimization
Russ Tedrake
w/ Alexandre Megretski, Pablo Parrilo
Slides available live at https://slides.com/d/0jpKUsI/live
or later at https://slides.com/russtedrake/2022-multibody


Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.
Available at: https://arxiv.org/abs/2101.11565


Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422




Goal #1: Motion planning/Model-Predictive Control
Global optimization-based planning for vehicles and manipulators with dynamic constraints and certificates of optimality / correctness
- Planning through contact
- Today: Collision-free planning

image credit: James Kuffner
Goal #2: Deeper connections between


Trajectory optimization
Sample-based planning
AI-style logical planning
Combinatorial optimization
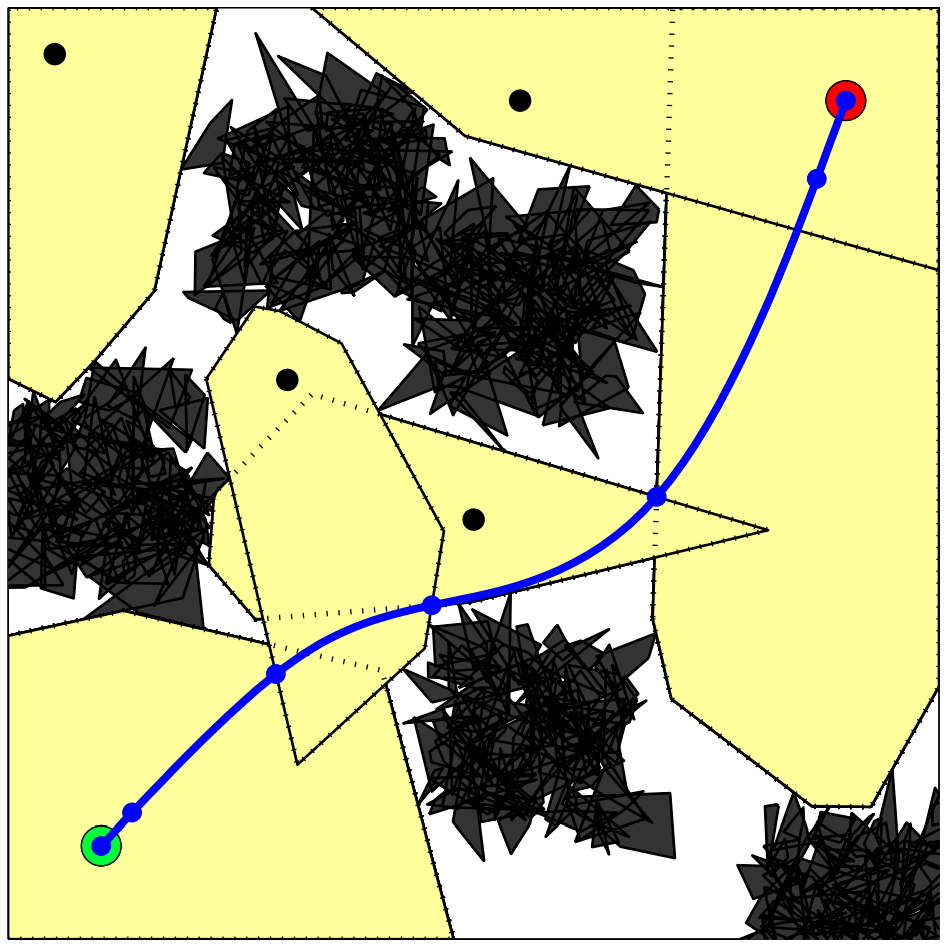
Motion planning with obstacles as an optimization
Running example: Shortest path around an obstacle
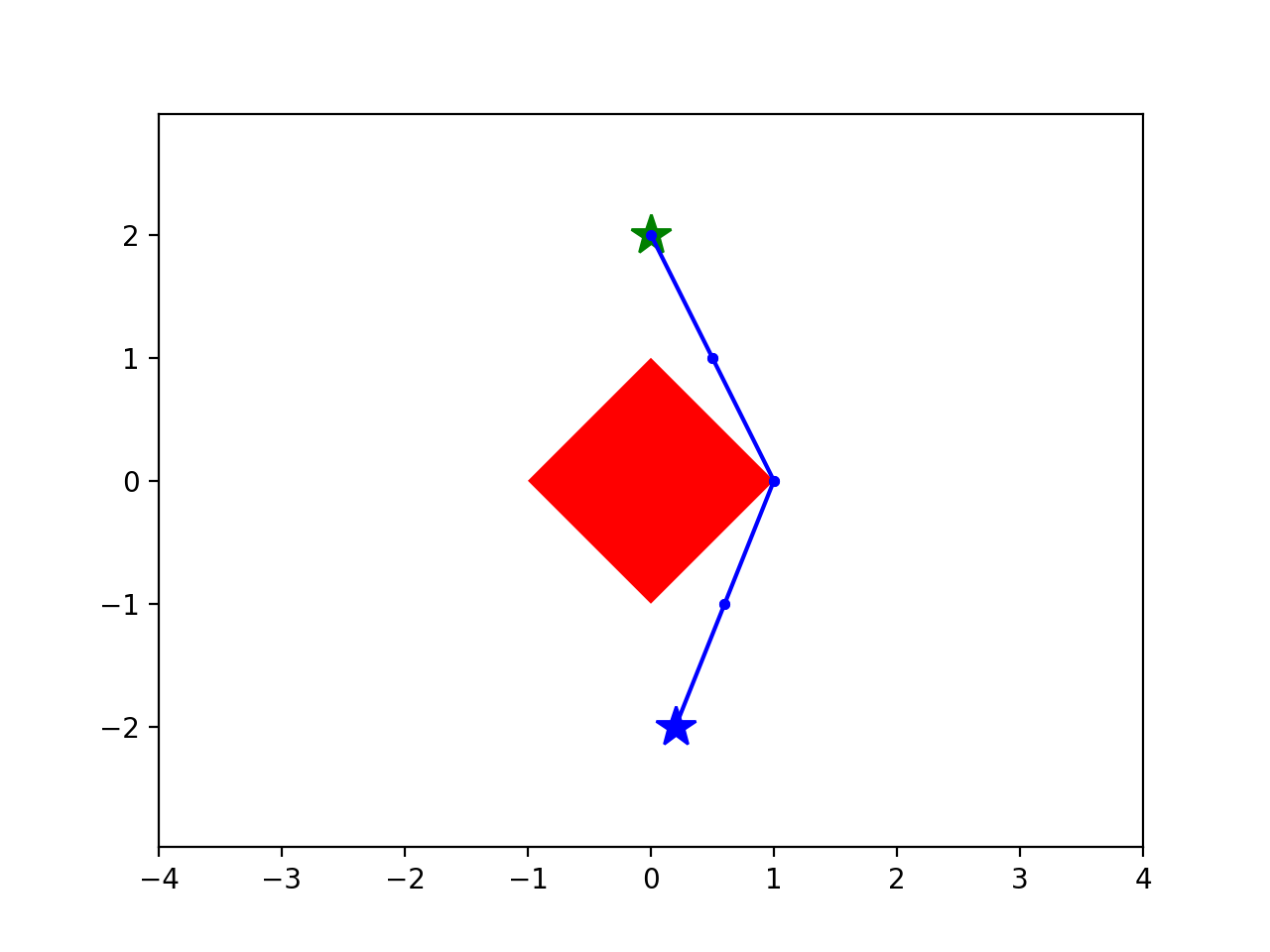
start
goal
Planning as a nonconvex optimization
A preview of the results...
Default playback at .25x
Two key ingredients
- The linear programming formulation of the shortest path problem on a discrete graph.
- Convex formulations of continuous motion planning (without obstacle navigation), for example:

Kinematic Trajectory Optimization
(for robot arms)
Planning as a mixed-integer convex program

goal
start
disjunctive
constraints
Planning as a mixed-integer convex program
Branch and bound performance
- Number of integer variables
- "Tightness" of the convex relaxation
- Motion planning transcription:
\(\Rightarrow\) Long solve times.
- Too many integer variables (false combinatorial complexity)
- Disjunctive programming leads to "loose" relaxations
Planning as a mixed-integer convex program
This is the convex relaxation
(it is very loose!).
Pablo asked the right question...
"We know that the LP formulation of the shortest path problem is tight. Why exactly are your relaxations so loose?"

- Vertices \(V\)
- (Directed) edges \(E\)
Graphs of Convex Sets


-
For each \(i \in V:\)
- Compact convex set \(X_i \subset \R^d\)
- A point \(x_i \in X_i \)
- Edge length given by a convex function \[ \ell(x_i, x_j) \]
Note: The blue regions are not obstacles.
Tightening the convex relaxation
- Tobia continued to study the convex relaxation on simple graphs.
- Pablo: "you're still missing a constraint"
Conservation of flow
Spatial conservation of flow
(this was the missing constraint!)
Motion planning with Graph of Convex Sets (GCS)

start
goal
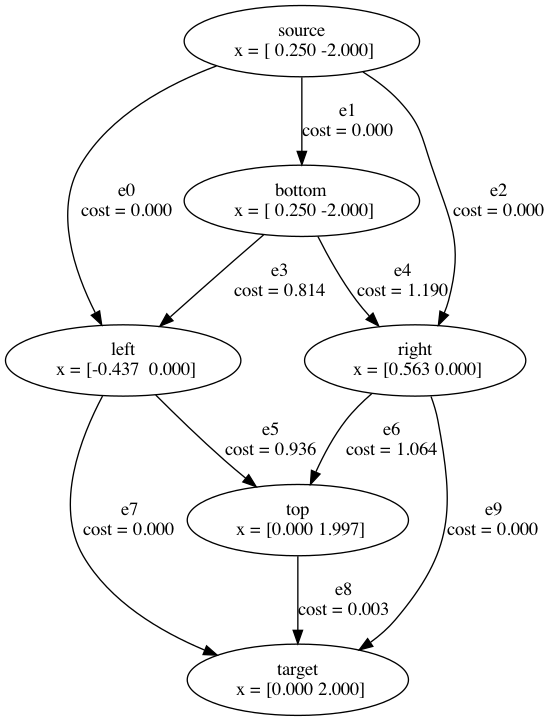
Motion planning with Graph of Convex Sets (GCS)
This is the convex relaxation
(it is tight!).
is the convex relaxation. (it's tight!)


Previous formulations were intractable; would have required \( 6.25 \times 10^6\) binaries.
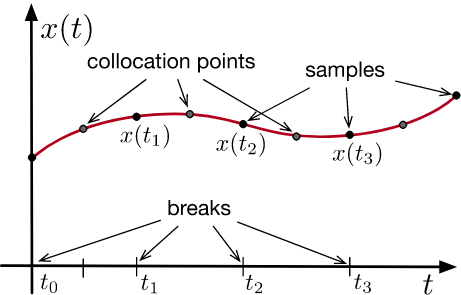
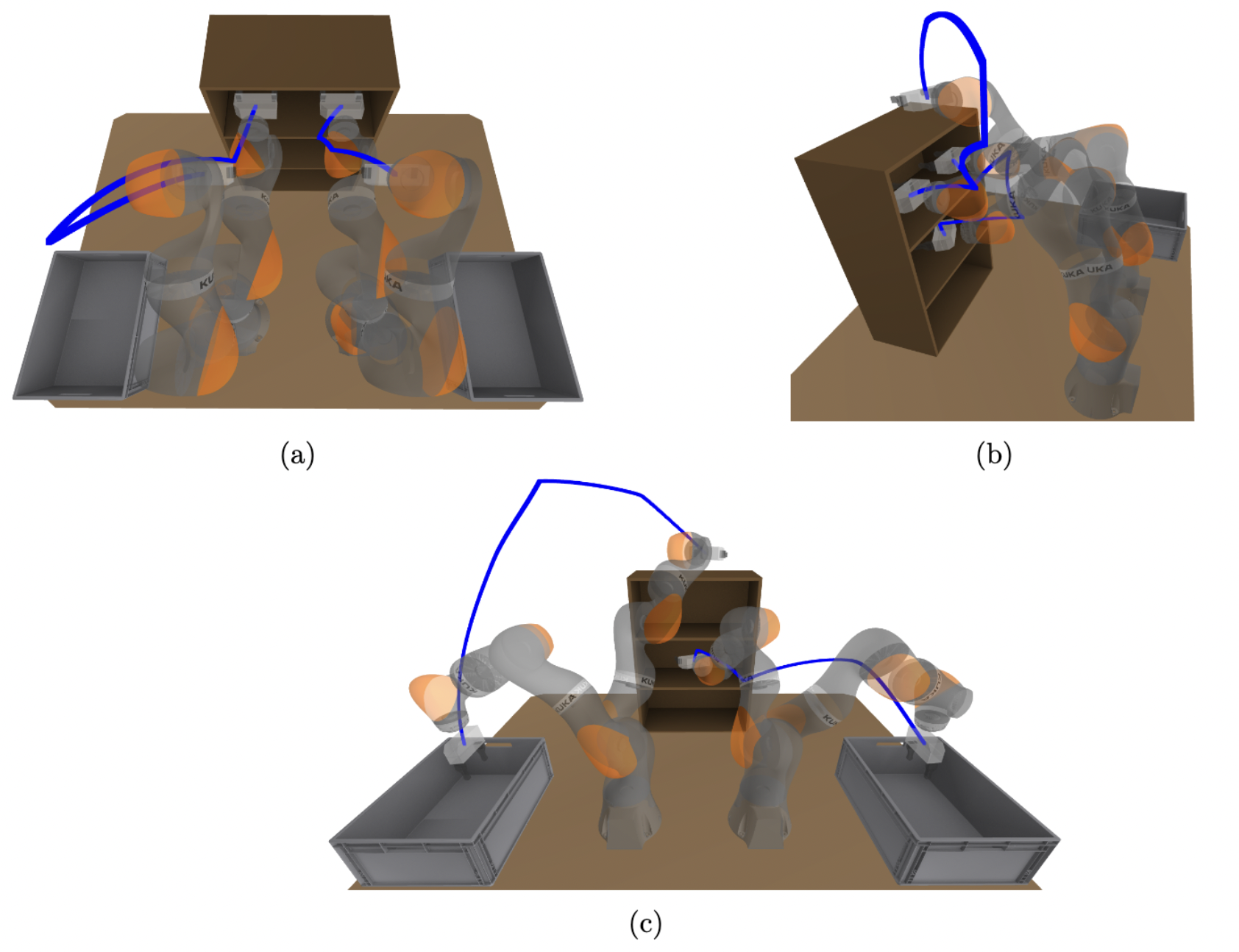
Formulating motion planning with differential constraints as a Graph of Convex Sets (GCS)





+ time-rescaling
duration
path length
path "energy"
note: not just at samples
continuous derivatives
collision avoidance
velocity constraints


minimum distance
minimum time
Transcription to a mixed-integer convex program, but with a very tight convex relaxation.
- Solve to global optimality w/ branch & bound orders of magnitude faster than previous work
- Solving only the convex optimization (+rounding) is almost always sufficient to obtain the globally optimal solution.

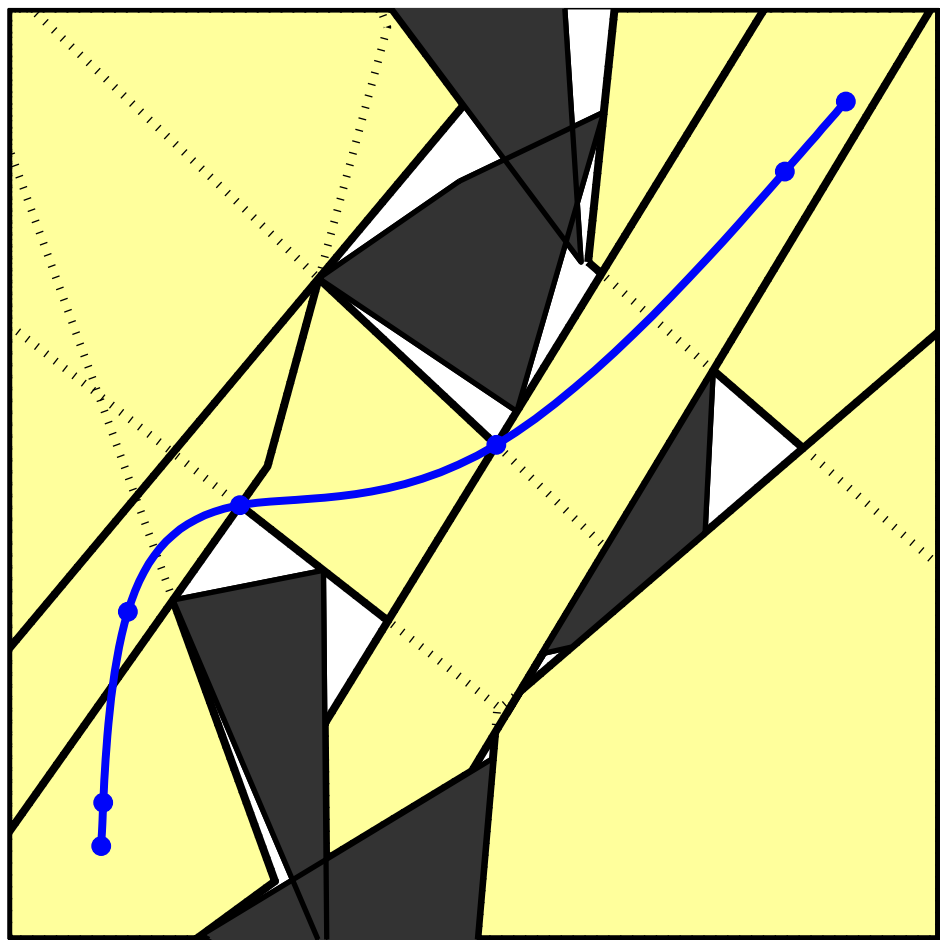
But how did we get the convex regions?


IRIS (Fast approximate convex segmentation). Deits and Tedrake, 2014
- Iteration between (large-scale) quadratic program and (relatively compact) semi-definite program (SDP)
- Scales to high dimensions, millions of obstacles
- ... enough to work on raw sensor data

Sampling-based motion planning

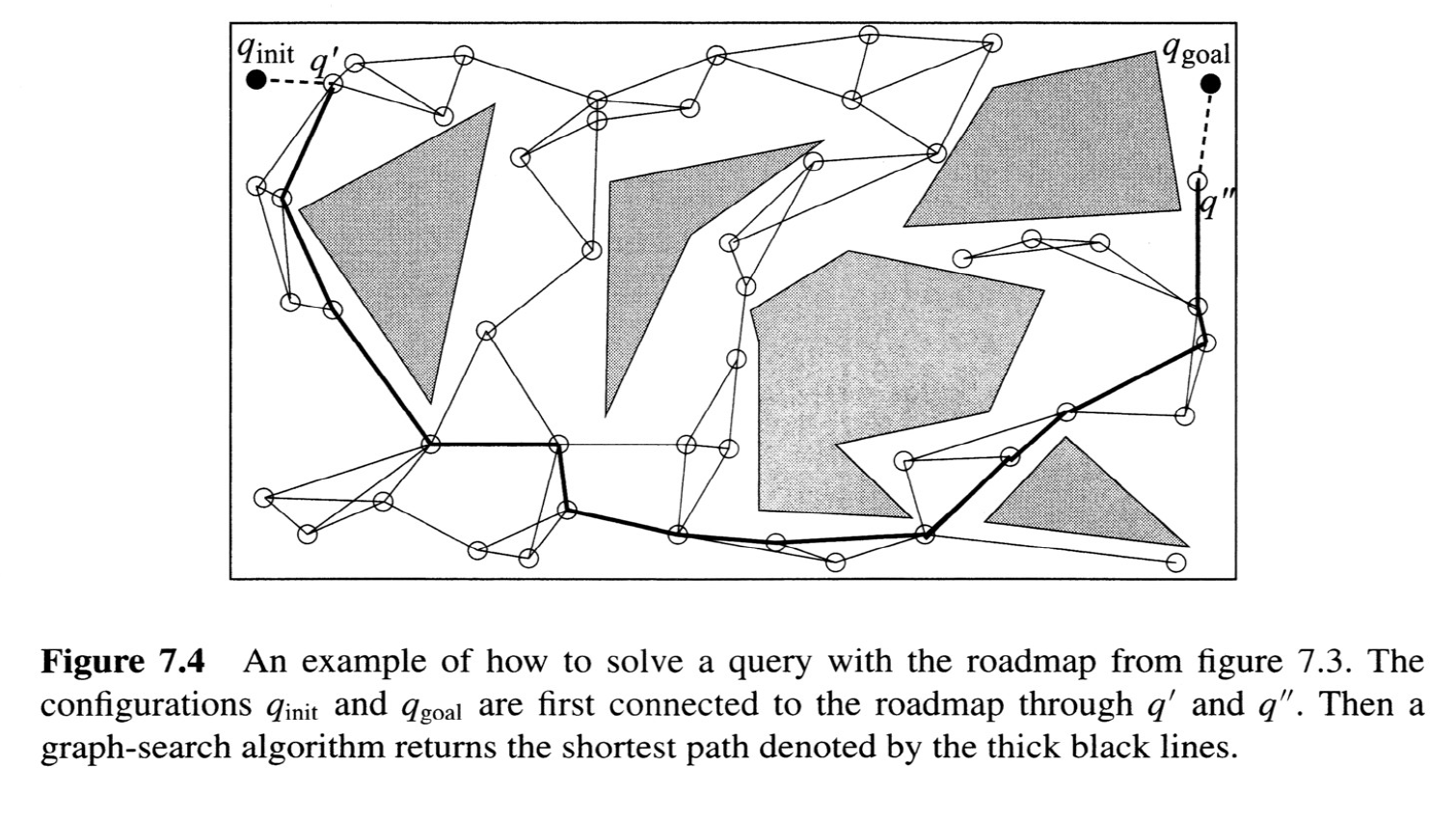
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.
- Guaranteed collision-free along piecewise polynomial trajectories
- Complete/globally optimal within convex decomposition
Graph of Convex Sets (GCS)
PRM
PRM w/ short-cutting


Preprocessor now makes easy optimizations fast!
Beyond motion planning
I've focused today on Graphs of convex sets (GCS) for motion planning
GCS is a more general modeling framework
- already orders of magnitude faster for a number of mixed-combinatorial continuous problems

As a motion planning tool
This is version 0.1 of a new framework.
- Already competitive
- We've provided a mature implementation
There is much more to do, for example:
- Add support for additional costs / constraints
- Dynamic collision geometry / moving obstacles
- Dual solution gives a cost-to-go; robustness to disturbances
- Work now on custom solver (with Pablo and Stephen Boyd)
- GCS can warm-start well
Summary
- New strong mixed-integer convex formulation for shortest path problems over convex regions
- reduces to shortest path as regions become points
- NP-hard; but strong formulation \(\Rightarrow\) efficient B&B
- Convex relaxations are often tight! \(\Rightarrow\) Rounding strategies
- Initial applications in vehicles and manipulator planning at dynamic limits
Give it a try:
pip install drake
sudo apt install drake
Goal #2: Deeper connections between





Trajectory optimization
Sample-based planning
AI-style logical planning
Combinatorial optimization
Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.
Available at: https://arxiv.org/abs/2101.11565


Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422



