Motion planning around obstacles with convex optimization
Russ Tedrake
Seminar on Computational Geometry and Robotics
Jan 18, 2023
Slides available live at https://slides.com/d/PbOeKDs/live
or later at https://slides.com/russtedrake/2023-cgr-seminar



Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.
Available at: https://arxiv.org/abs/2101.11565


Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422




Goal #1: Motion planning
Efficient algorithms for (approximate) global optimization-based planning for manipulators with dynamic constraints
- Planning through contact
- Today: Collision-free planning

image credit: James Kuffner
Goal #2: Deeper connections between


Trajectory optimization
Sample-based planning
AI-style logical planning
Combinatorial optimization
RRT* by Karaman et al

start
goal
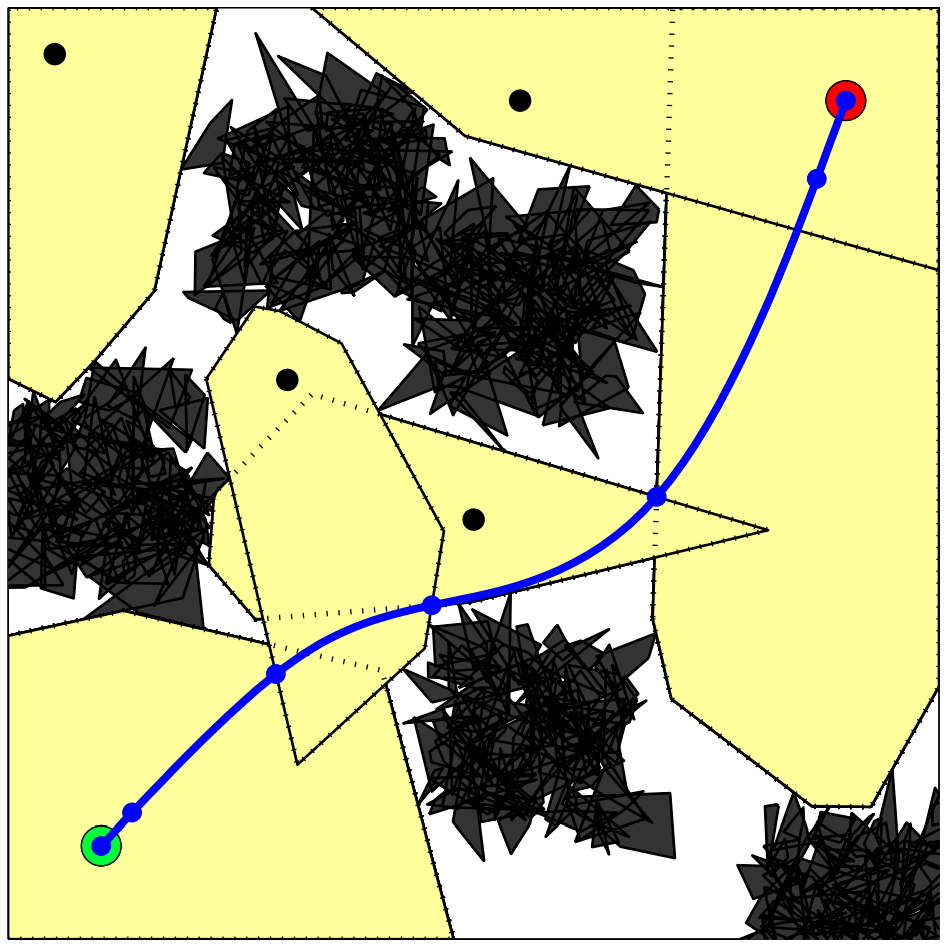
Motion planning as an optimization
Running example: Shortest path around an obstacle
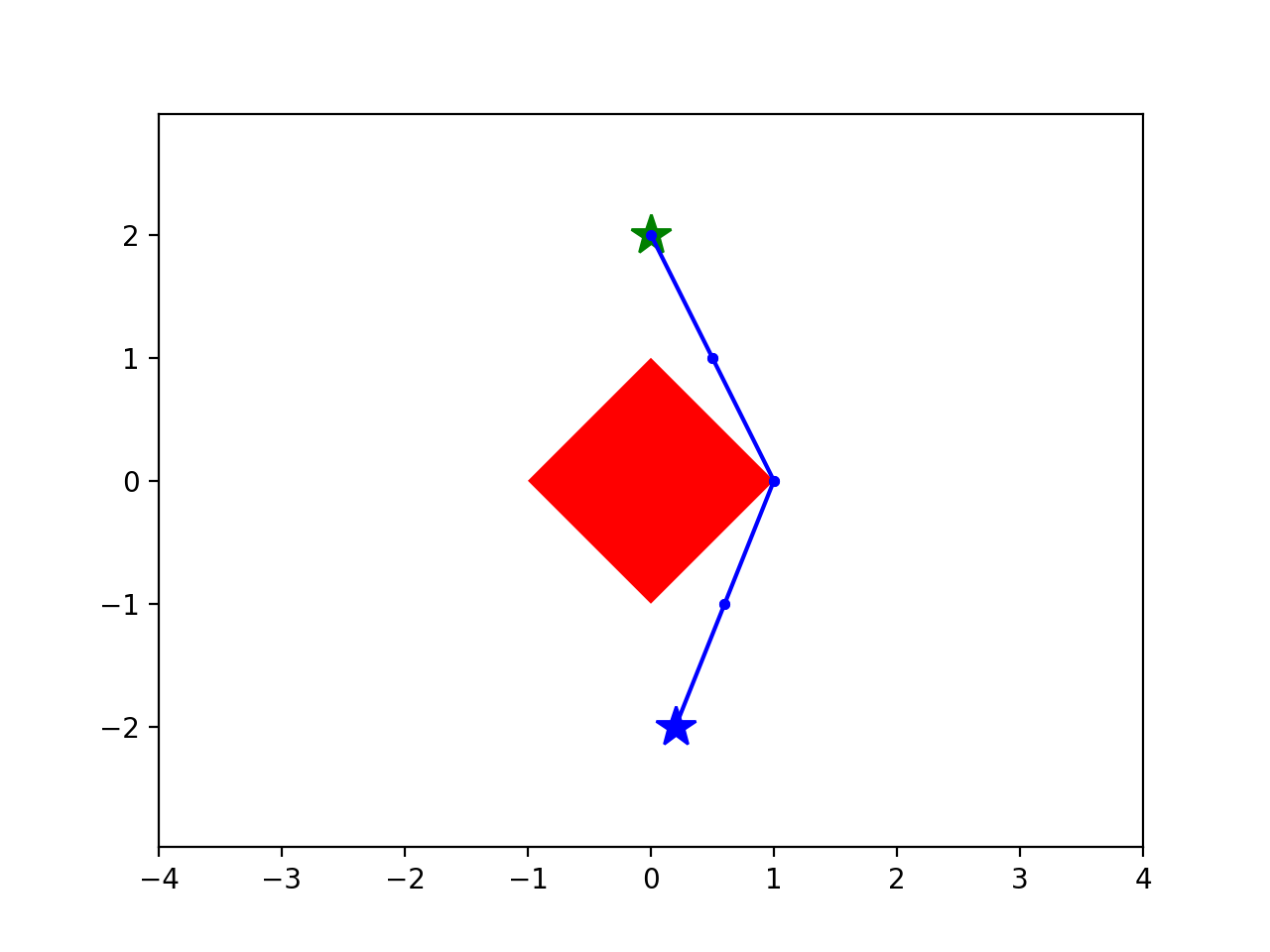
start
goal
Motion planning as a (nonconvex) optimization

start
goal
fixed number of samples
collision-avoidance
(outside the \(L^1\) ball)
nonconvex
Planning as a (nonconvex) optimization
A preview of the results...
Default playback at .25x
Three key ingredients
- The linear programming formulation of the shortest path problem on a discrete graph.
- Convex formulations of continuous motion planning (without obstacle navigation), for example:
3. Approximate convex decompositions of configuration space

Kinematic Trajectory Optimization
(for robot arms)
Planning as a mixed-integer convex program

goal
start
disjunctive
constraints
Planning as a mixed-integer convex program
Mixed-integer programs
"Convex relaxation" replaces this with:
"Mixed-integer convex" iff \(f\) and \(g\) are convex.
Convex relaxation is "tight" when the relaxed solution is a solution to the original problem.
Branch and bound
Convex relaxations provide lower bounds
Feasible solutions provide upper bounds
convex
convex
convex
convex
convex
Branch and bound performance
- Number of integer variables
- "Tightness" of the convex relaxation
- Motion planning transcription:
\(\Rightarrow\) Long solve times.
- Too many integer variables (false combinatorial complexity)
- Disjunctive programming leads to "loose" relaxations
Planning as a mixed-integer convex program
This is the convex relaxation
(it is very loose!).
Pablo asked the right question...
"We know that the LP formulation of the shortest path problem is tight. Why exactly are your relaxations so loose?"

- Vertices \(V\)
- (Directed) edges \(E\)
Traditional Shortest Path as a Linear Program (LP)
\(\varphi_{ij} = 1\) if the edge \((i,j)\) in shortest path, otherwise \(\varphi_{ij} = 0.\)
\(c_{ij} \) is the (constant) length of edge \((i,j).\)

"flow constraints"
binary relaxation
path length
Graphs of Convex Sets


-
For each \(i \in V:\)
- Compact convex set \(X_i \subset \R^d\)
- A point \(x_i \in X_i \)
- Edge length given by a convex function \[ \ell(x_i, x_j) \]
Note: The blue regions are not obstacles.
New shortest path formulation
Classic shortest path LP
now w/ Convex Sets
New shortest path formulation
Non-negative scaling of a convex set is still convex (e.g. via "perspective functions")
Achieved orders of magnitude speedups.
Tightening the convex relaxation
- Tobia continued to study the convex relaxation on simple graphs.
- Pablo: "you're still missing a constraint"
Conservation of flow
Spatial conservation of flow
(this was the missing constraint!)
Motion planning with Graph of Convex Sets (GCS)

start
goal
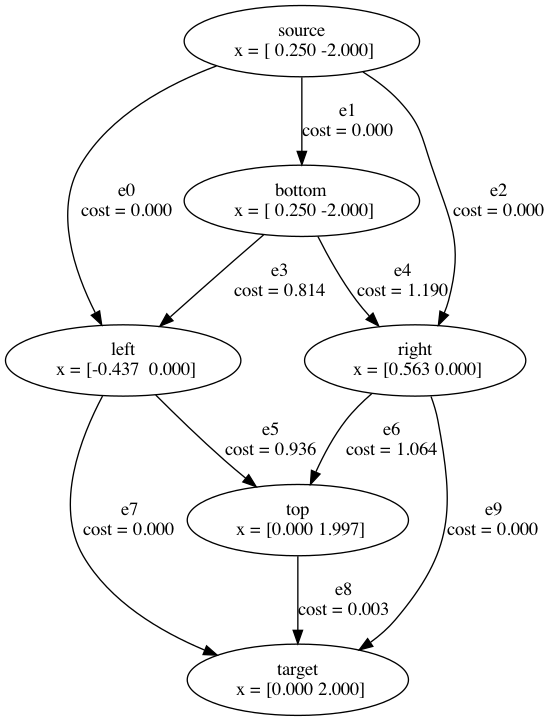
Motion planning with Graph of Convex Sets (GCS)
This is the convex relaxation
(it is tight!).
is the convex relaxation. (it's tight!)


Previous formulations were intractable; would have required \( 6.25 \times 10^6\) binaries.
Euclidean shortest path
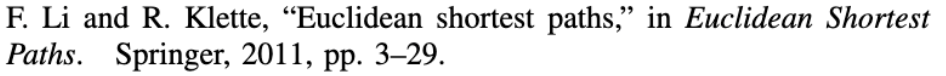
- Finding the shortest path from A to B while avoiding polygonal obstacles (“Euclidean shortest path”):
- Solvable in polytime in 2D (with a visibility graph)
- NP-hard from 3 dimensions on
- For the 3D case there exists an approximation algorithm which gives you \(\epsilon\)-optimality in poly time
- Nothing is known for dimension \(\ge 4\)
- New formulation:
- Provides polynomial-time algorithm for dimension \(\ge 4\) that is often tight.
- Solves a more general class of problems (e.g. can add dynamic constraints).
- When sets \( X_i \) are points, reduces to standard LP formulation of the shortest path (known to be tight).
- There are instances of this problem that are NP-hard.
- We give simple examples where relaxation is not tight.
- Can add (piecewise-affine) dynamic constraints on pairs \( (x_i,x_j). \)
Remarks
Example: "Footstep planning" with \(x_{n+1}=Ax_n + Bu_n\)

| Previous best formulations | New formulation | |
|---|---|---|
| Lower Bound (from convex relaxation) |
7% of MICP | 80% of MICP |
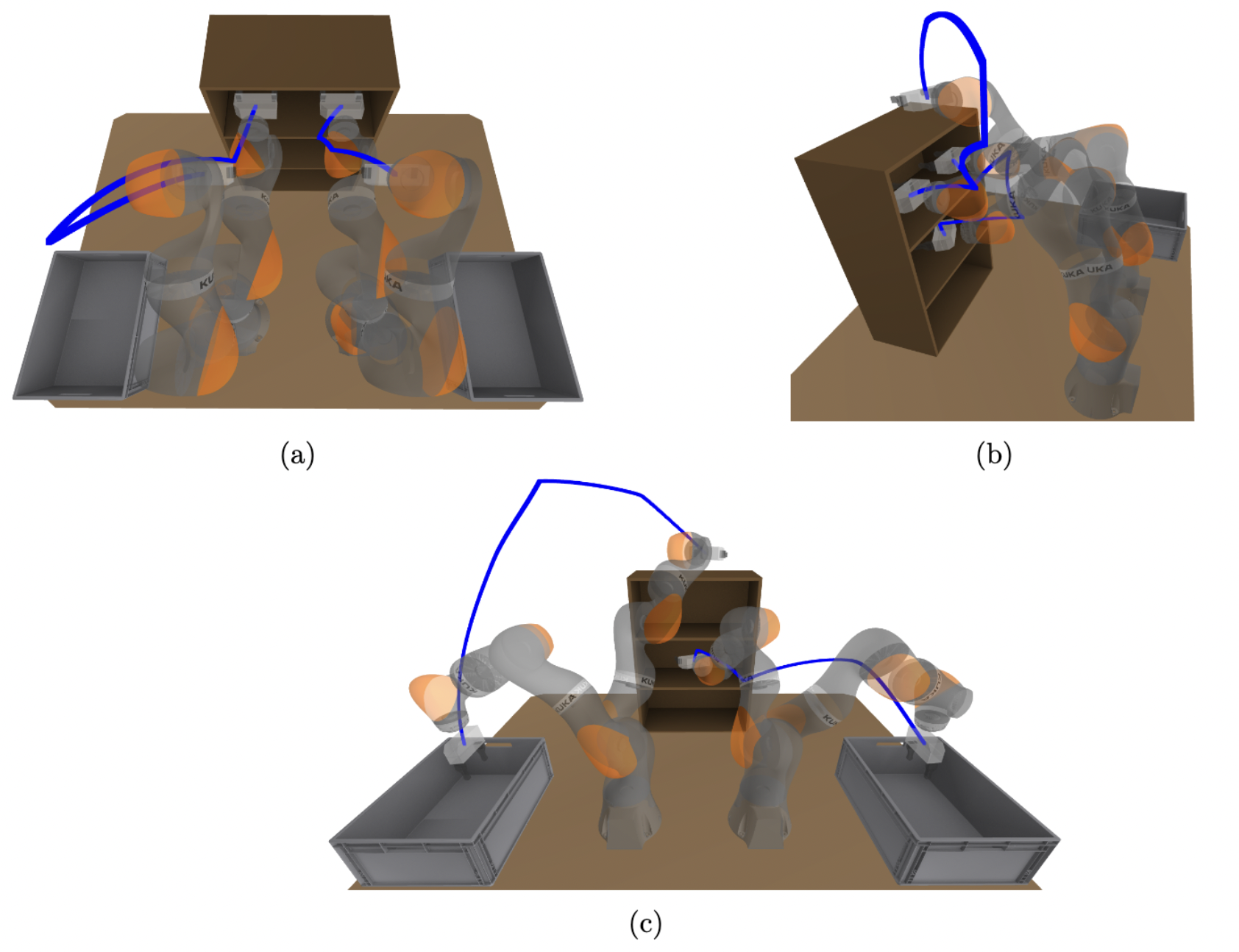
Formulating motion planning with differential constraints as a Graph of Convex Sets (GCS)





+ time-rescaling
duration
path length
path "energy"
note: not just at samples
continuous derivatives
collision avoidance
velocity constraints


minimum distance
minimum time
For Dan
For Dan
Transcription to a mixed-integer convex program, but with a very tight convex relaxation.
- Solve to global optimality w/ branch & bound orders of magnitude faster than previous work
- Solving only the convex optimization (+rounding) is almost always sufficient to obtain the globally optimal solution.
As Elon Rimon says "performance bounds are missing"

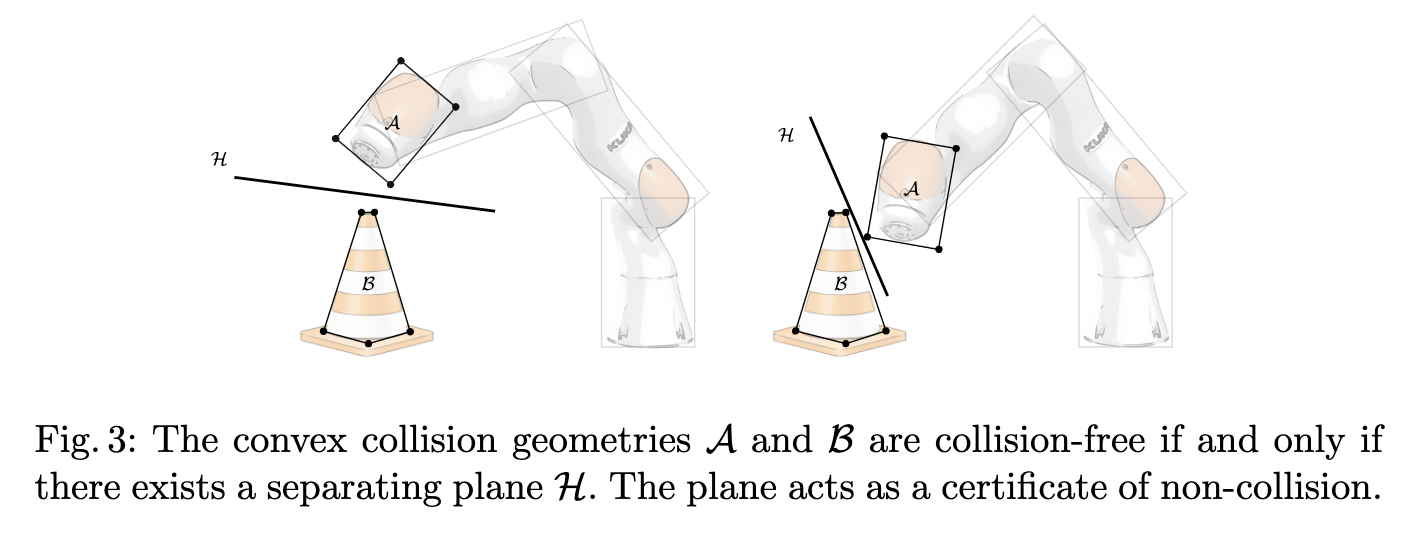
But how did we get the convex regions?


IRIS (Fast approximate convex segmentation). Deits and Tedrake, 2014
- Iteration between (large-scale) quadratic program and (relatively compact) semi-definite program (SDP)
- Scales to high dimensions, millions of obstacles
- ... enough to work on raw sensor data
Configuration-space regions
- Original IRIS algorithm assumed obstacles were convex
- Two new extensions for C-space:
- Nonlinear optimization for speed
- Sums-of-squares for rigorous certification

WAFR 2022;
Journal version out this month.
Sums-of-Squares formulation
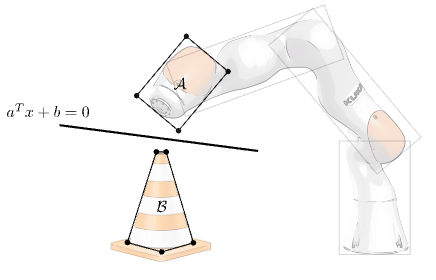
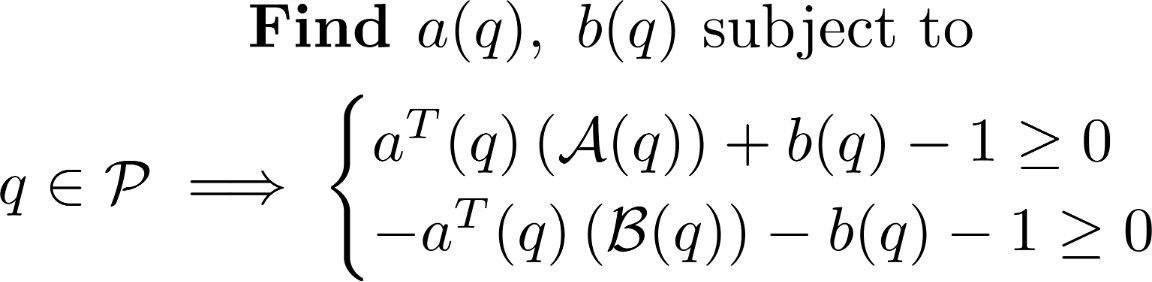
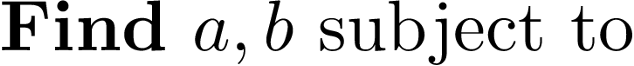
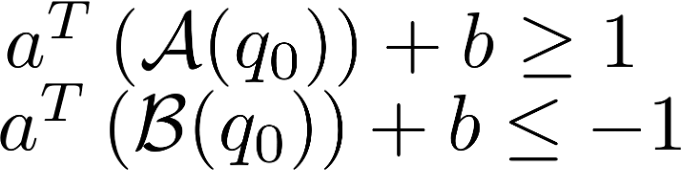
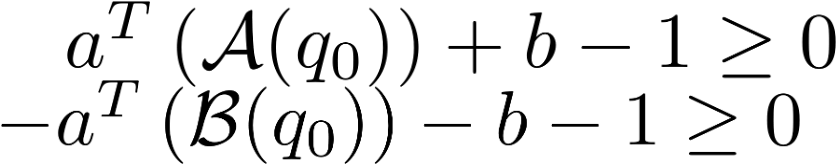
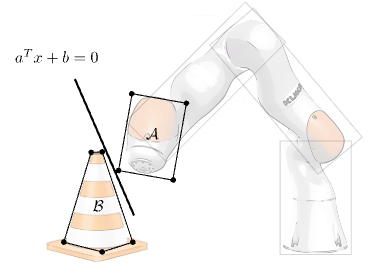
Solve using rational polynomial kinematics
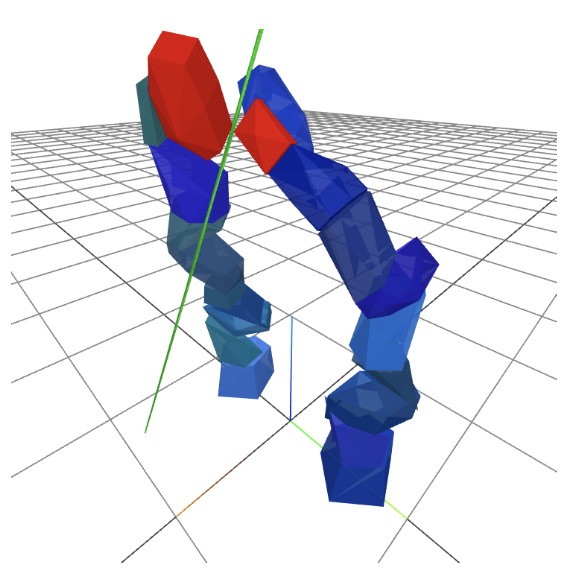
The separating plane (green) is the non-collision certificate between the two highlighted polytopic collision geometries (red), with a distance of 7.3mm.
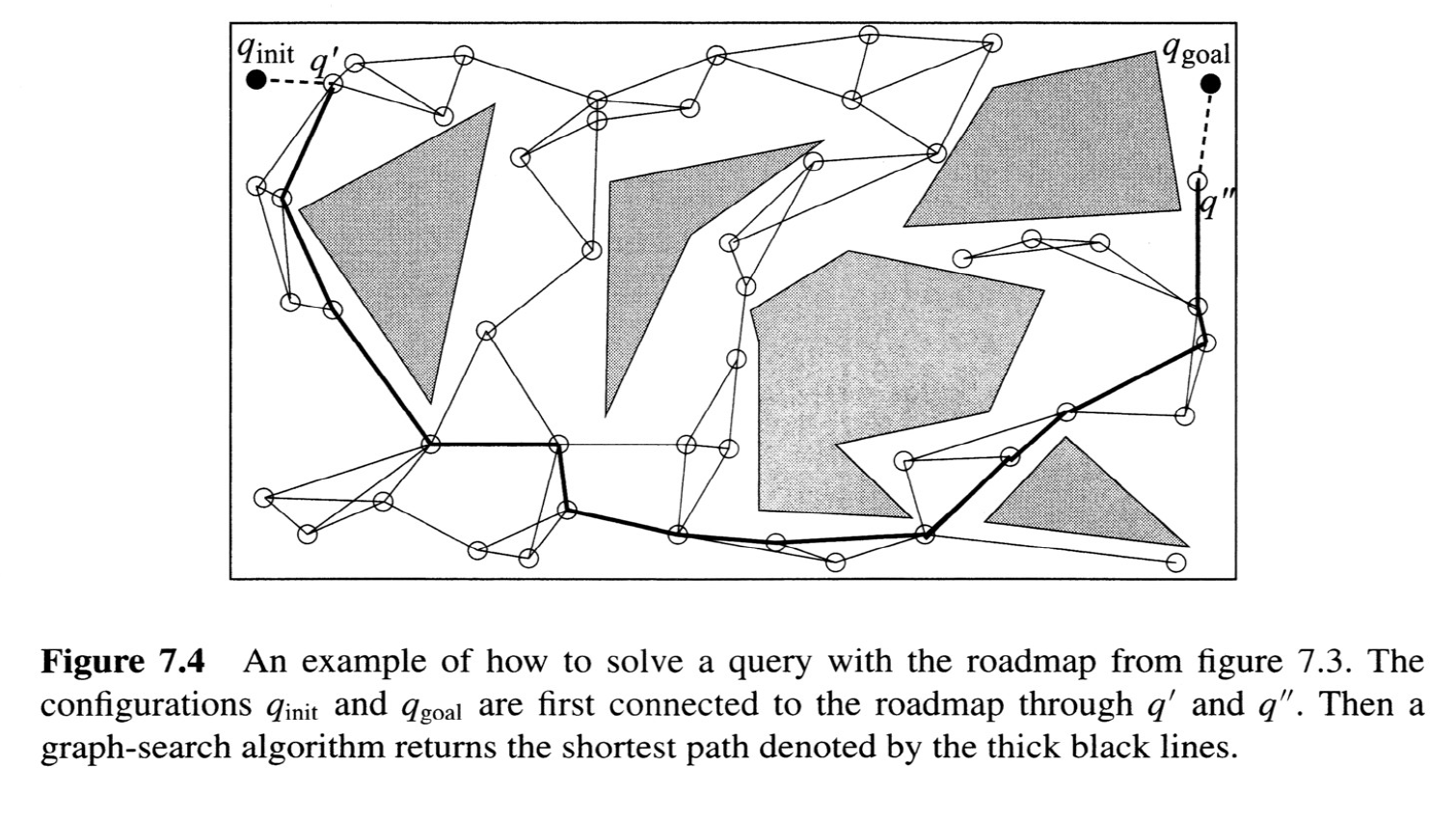
Sampling-based motion planning

The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.
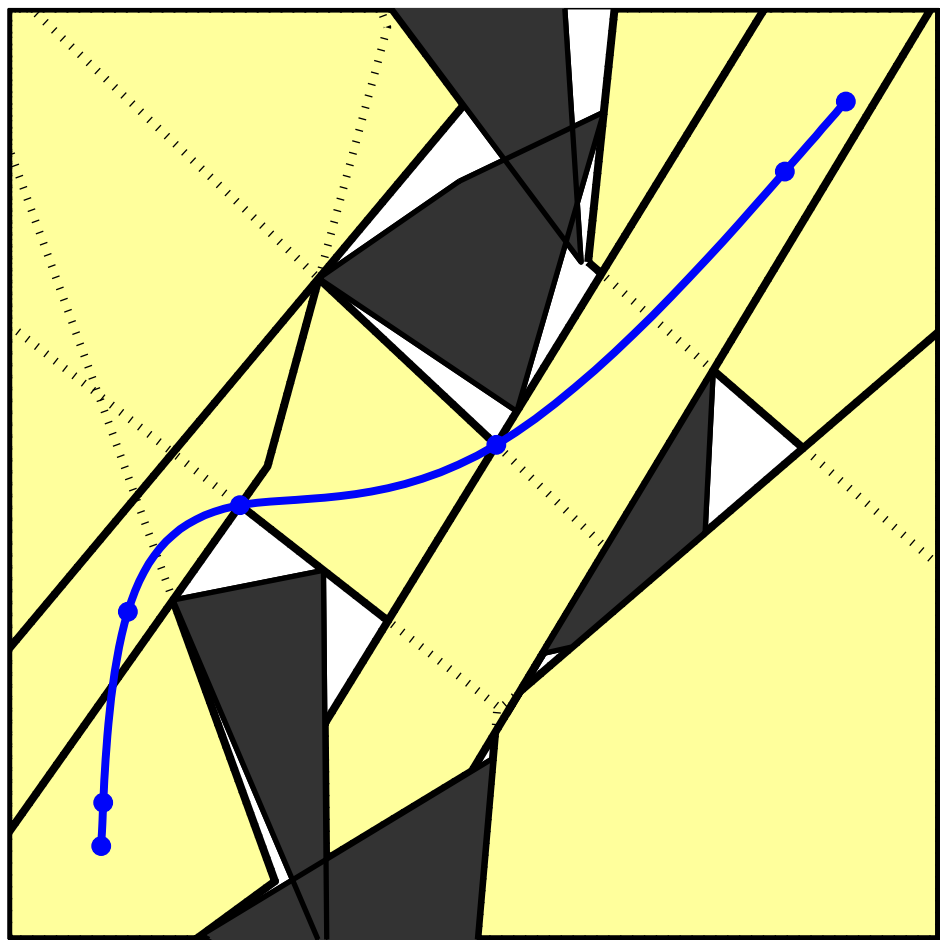
- Guaranteed collision-free along piecewise polynomial trajectories
- Complete/globally optimal within convex decomposition
Graph of Convex Sets (GCS)
PRM
PRM w/ short-cutting


Preprocessor now makes easy optimizations fast!
Geometry Problems
- We don't yet understand rigorously what defines optimal convex decompositions for this planner
- closely related to the maximum vertex hidden set problem and visibility graphs
- subtle costs/benefits of overlapping regions
- subtle trade-offs between coverage and complexity of the sets
- closely related to the maximum vertex hidden set problem and visibility graphs

Extensions to Non-Euclidean spaces
- Constrain IRIS regions with geodesic convexity
- Assign a chart to each vertex
- Pullbacks define all of the natural changes of coordinates
with Tommy Cohn, Mark Petersen, and Max Simchowitz
Extensions to Non-Euclidean spaces
- Constrain IRIS regions with geodesic convexity
- Assign a chart to each vertex
- Pullbacks define all of the natural changes of coordinates
with Tommy Cohn, Mark Petersen, and Max Simchowitz
Task and motion planning
GCS version (top down)

Task and motion planning with GCS
Prelimary results by Savva Morozov
Beyond motion planning
I've focused today on Graphs of convex sets (GCS) for motion planning
GCS is a more general modeling framework
- already orders of magnitude faster for a number of mixed-combinatorial continuous problems

As a motion planning tool
This is version 0.1 of a new framework.
- Already competitive
- We've provided a mature implementation
There is much more to do, for example:
- Add support for additional costs / constraints
- Dynamic collision geometry / moving obstacles
- Working on a custom solver with Stephen Boyd
- GCS can warm-start well


"Hydroelastic contact" as implemented in Drake
Summary
- New strong mixed-integer convex formulation for shortest path problems over convex regions
- reduces to shortest path as regions become points
- NP-hard; but strong formulation \(\Rightarrow\) efficient B&B
- Convex relaxations are often tight! \(\Rightarrow\) Rounding strategies
- Initial applications in manipulator planning at dynamic limits
Give it a try:
pip install drake
sudo apt install drake
Goal #2: Deeper connections between





Trajectory optimization
Sample-based planning
AI-style logical planning
Combinatorial optimization
Online classes (videos + lecture notes + code)
http://manipulation.mit.edu
http://underactuated.mit.edu
Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.
Available at: https://arxiv.org/abs/2101.11565


Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422



