From Theory to Production (and Back)

A Collaboration on Optimization and Learning for Robotic Manipulation

Russ Tedrake

MIT–Amazon Science Hub Robotics Research Day 2025

A golden age for robotics

Jensen @ CES 2025

A golden age for robotics

Important roles to play for both industry and academia.

Science Hub Project: Dynamic Manipulation

"... to move beyond the state-of-the-art in fast dynamic, contact-rich object manipulation and data-driven adaptation [...] for high-speed manipulation of highly diverse objects in densely occupied spaces."

Robin: https://www.amazon.science/latest-news/amazon-robotics-see-robin-robot-arms-in-action

Cardinal: https://www.aboutamazon.com/news/operations/10-years-of-amazon-robotics-how-robots-help-sort-packages-move-product-and-improve-safety

Sparrow: https://www.aboutamazon.com/new/transportation/amazon-robot-sparrow-streamlines-order-fulfillment-process

From Theory to Production (and Back)

Collaboration

  • Amazon scientists are integral part of our research project meetings
  • Numerous co-authored papers
  • Sharing code (via open source) and data
  • Internships (e.g., Savva doing extended internship right now)
  • Tobia joined AR as a postdoc before starting his faculty position
  • Lu will joint Amazon FAR lab after finishing her PhD this fall.

Today: I'll share 3 storylines

2021

2025

Motion Planning (w/ Pablo Parrilo)

"Real2Sim" (w/ Phil Isola)

Theory of Visuomotor Control w/ Generative AI

(w/ Asu and Pablo)

Motion Planning

2021

2025

Motion Planning

"Real2Sim"

Theory of Visuomotor Control

A new approach to motion planning

Claims:

  • Find better plans faster than sampling-based planners
  • Avoid local minima from trajectory optimization
  • Can guarantee paths are collision-free
  • Naturally handles dynamic limits/constraints
  • Scales to big problems (e.g. multiple arms)
  • Important for Amazon: fast and consistent solve times

Graphs of Convex Sets (GCS)

(discrete + continuous planning and control)

+ many amazing students and AR advocates/collaborators

Graphs of Convex Sets with Applications to Optimal Control and Motion Planning.

Tobia Marcucci. PhD Thesis, MIT, 2024.  
EECS George M. Sprowls PhD Thesis Award in Artificial Intelligence and Decision Making

Optimal Control

\begin{align*} \min_{x[\cdot], u[\cdot]}\quad& \sum_{n=0}^N \ell(x[n], u[n])\\ \text{s.t.}\quad& x[n+1] = f(x[n],u[n])\\ & \text{additional constraints} \end{align*}

There are two cases that we completely understand:

  • Tabular/Markdov Decision Process (discrete state & action),
  • Linear+Convex (e.g. LQR, linear MPC).

but robotics problems often have elements of both...

Planning and control through contact

Two stages:

  1. Discrete: Plan contact sequence (e.g. footsteps)
  2. Continuous: Nonlinear MPC

Task and motion planning

Integrate:

  • Discrete: Large-scale discrete planners (e.g. Fast downward)
  • Continuous: e.g. Sampling-based planners

start

goal

  • Discrete/Combinatorial (e.g. over homotopy classes)
  • Continuous/Smooth optimization (over curves)

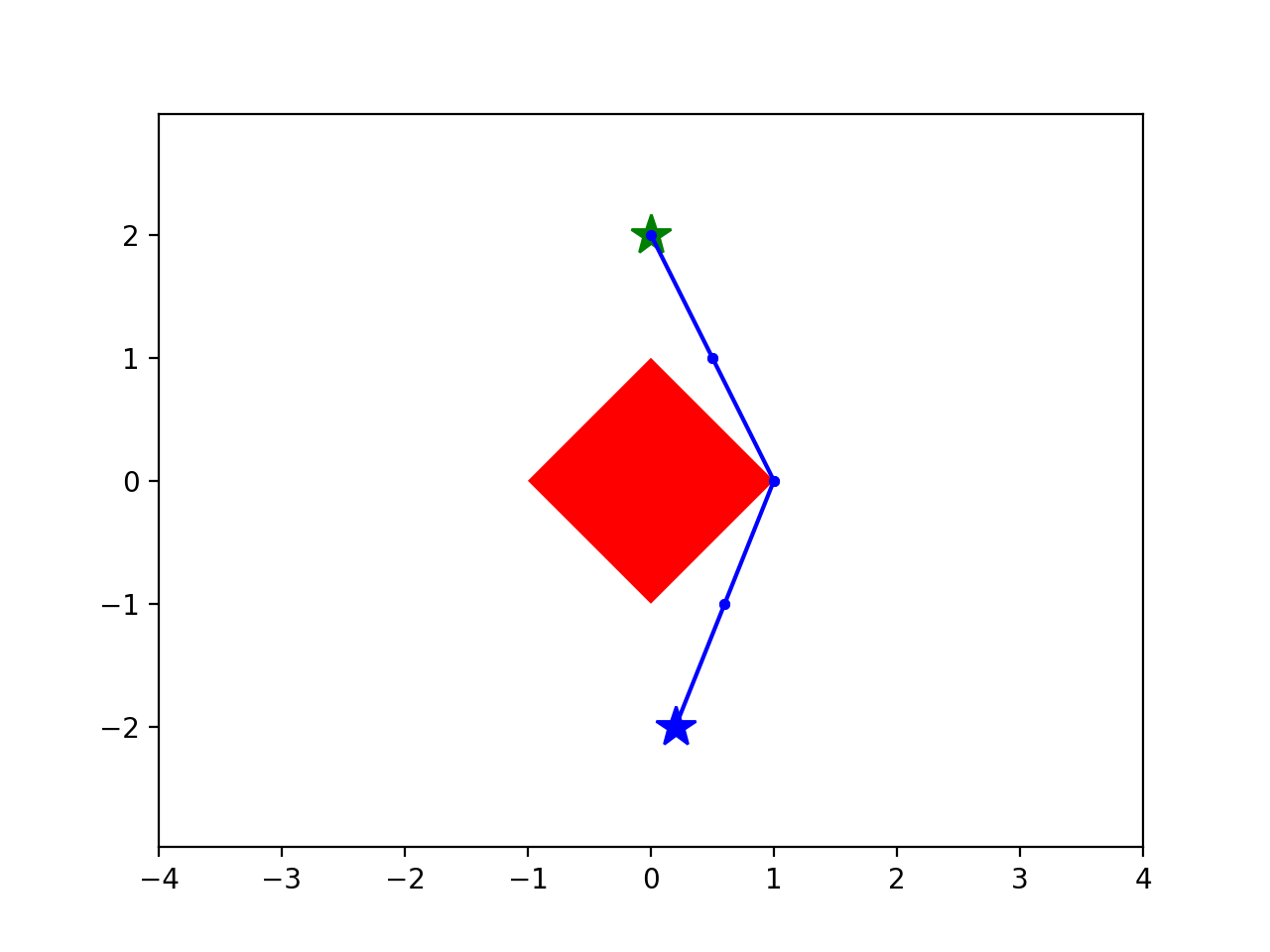
(even) Collision-free motion planning

Combinatorial: Sampling-based motion planning

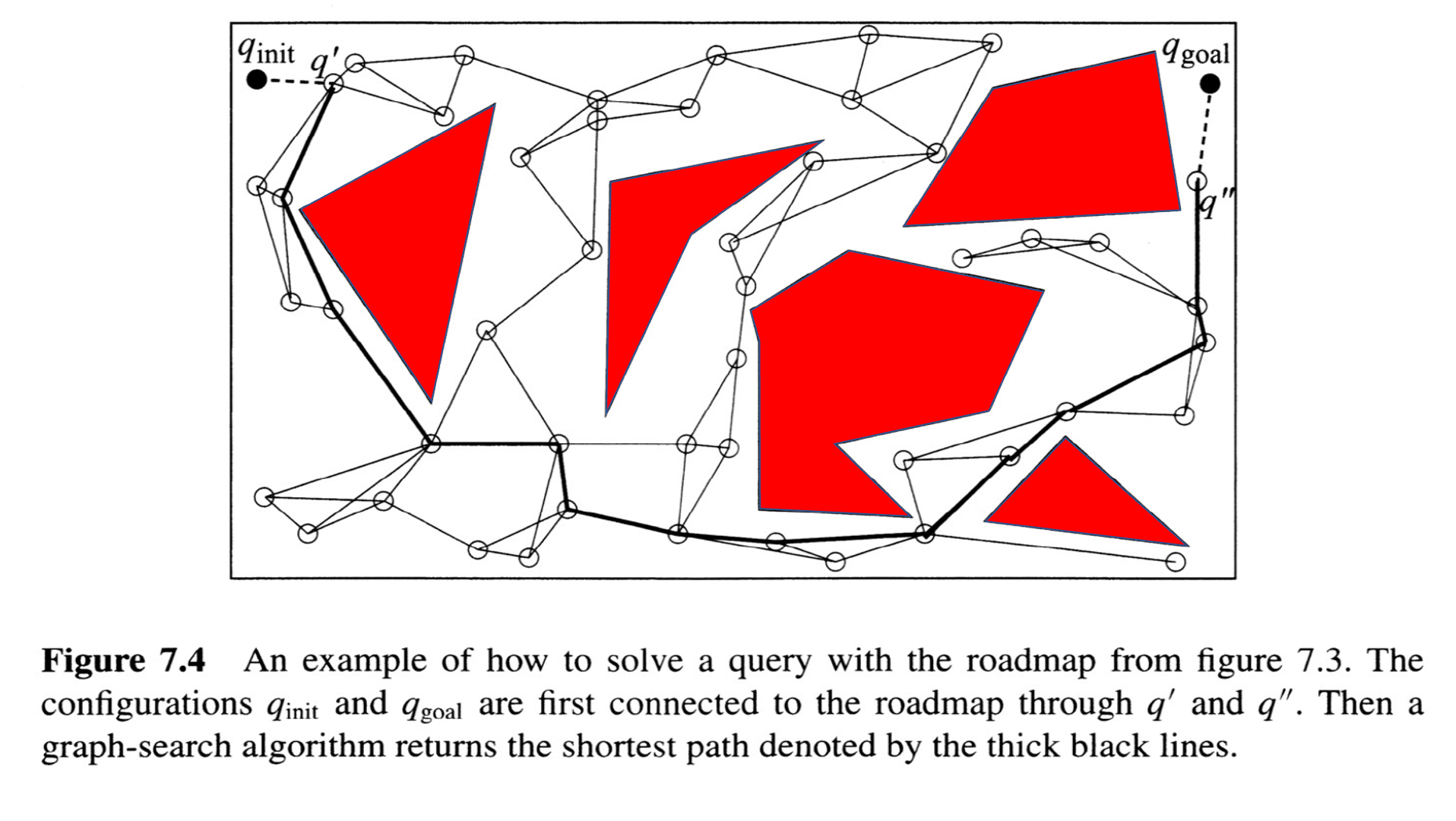
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.

Smooth: Trajectory Optimization

Graphs of convex sets (GCS) offers a new relaxation / modeling framework for joint discrete + continuous optimization

Traditional Shortest Path as a Linear Program (LP)

\(\varphi_{ij} = 1\) if the edge \((i,j)\) in shortest path, otherwise \(\varphi_{ij} = 0.\)

\(c_{ij} \) is the (constant) length of edge \((i,j).\)

\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\ \mathrm{s.t.} \quad & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si}, && \forall i \in V, \\ & \varphi_{ij} \in \{0, 1\}, && \forall (i,j) \in E. \end{aligned}

"flow constraints"

binary relaxation

path length

\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\ \mathrm{s.t.} \quad & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si}, && \forall i \in V, \\ & \varphi_{ij} \ge 0, && \forall (i,j) \in E. \end{aligned}

Graphs of Convex Sets

 

  • For each \(i \in V:\)
    • Compact convex set \(X_i \subset \R^d\)
    • A point \(x_i \in X_i \) 
  • Edge length given by a convex function \[ \ell(x_i, x_j) \]

Note: The blue regions are not obstacles.

GCS shortest path formulation

\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\ \mathrm{s.t.} \quad & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si}, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

Classic shortest path LP

\begin{aligned} \min_{\varphi,x} \quad & \sum_{(i,j) \in E} \ell_{ij}(x_i, x_j) \varphi_{ij} \\ \mathrm{s.t.} \quad & x_i \in X_i, && \forall i \in V, \\ & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si} \le 1, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

now w/ Convex Sets

GCS "Machinery"

\begin{aligned} \min_{\varphi,x} \quad & \sum_{(i,j) \in E} \ell_{ij}(x_i, x_j) \varphi_{ij} \\ \mathrm{s.t.} \quad & x_i \in X_i, && \forall i \in V, \\ & \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si} \le 1, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}
  • Transcribe bilinear form into MI-convex
  • Multiply discrete constraints w/ continuous constraints for efficient and often tight convex relaxation 

Traveling Salesperson

\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\ \mathrm{s.t.} \quad & \sum_{j \in E_i^{out}} \varphi_{ij} = \sum_{j \in E_i^{in}} \varphi_{ji} = 1, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}
  • famously NP-hard
  • apply GCS machinery for efficient MIP generalization
  • orders of magnitude faster than previous "TSP w/ neighborhood" formulations

Graph optimization problems

Shortest path, Traveling salesperson, minimum spanning tree, bipartite matching, facility location, ...

Ex: Minimum spanning tree

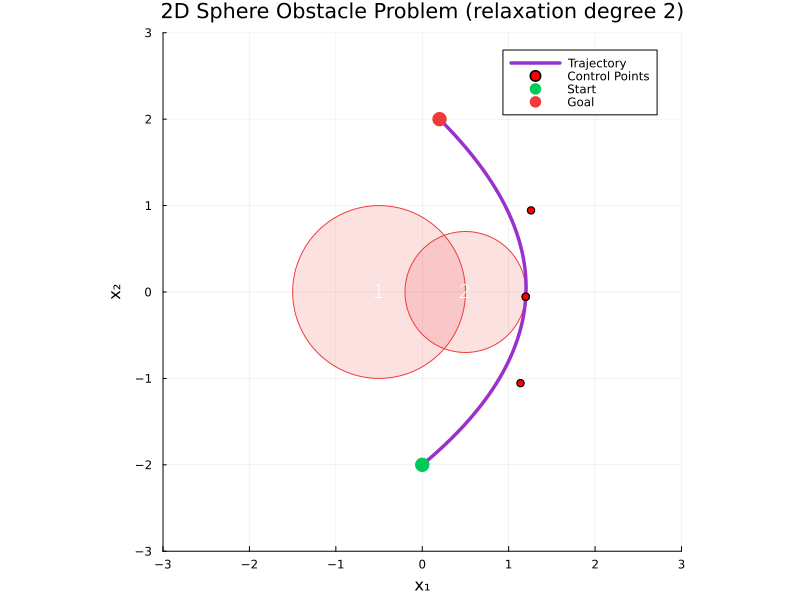
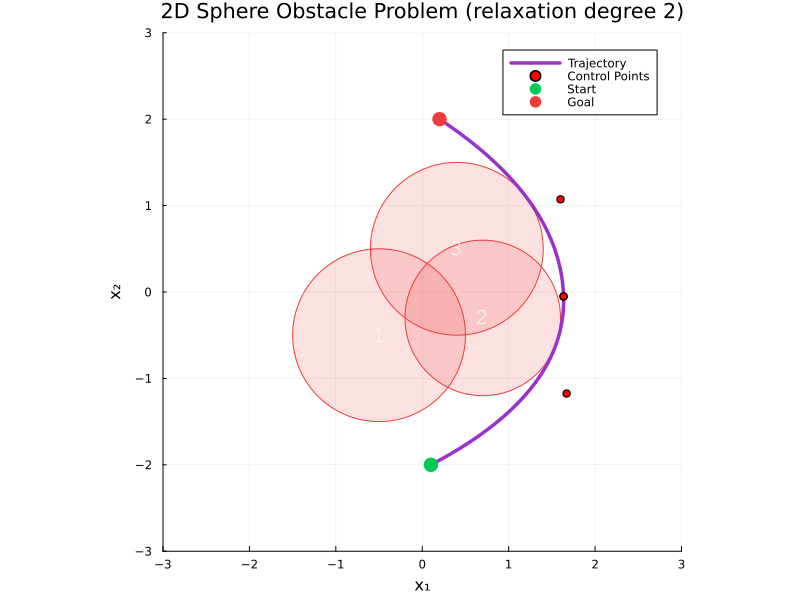
Ex: Minimum-volume sphere collision geometry (as facility location on a GCS)

Tabular + Linear MPC

Finite MDP (e.g. w/ deterministic transitions) is shortest path

When sets are points, GCS transcription yields exactly the well-known linear program (LP) for shortest path.

Tabular + Linear MPC

\[ \min_{x[\cdot],u[\cdot]} \sum_{n=0}^N x_n^T Q x_n + u_n^T Ru_n \\ \text{s.t. } x_{n+1} = Ax_n + Bu_n \]

Sets \( X_n: (x_n, u_n) \)

Edge cost

Edge constraint

n=0

n=1

n=2

n=N

\( \cdots \)

For a serial chain, GCS will generate exactly the familiar MPC transcriptions, e.g. quadratic programs (QPs)

Mixed logical dynamical systems (MLDS)

e.g. for hybrid trajectory optimization

n=0

n=1

n=N

...

\[ \min_{x[\cdot],u[\cdot]} \sum_{n=0}^N x_n^T Q_i x_n + u_n^T R_iu_n \\ \text{s.t. } x_{n+1} = A_ix_n + B_iu_n \\ \text{iff } (x_n,u_n) \in D_i \] 

start

goal

          is the convex relaxation.  (it's tight!)

Previous formulations were intractable; would have required \( 6.25 \times 10^6\) binaries.

minimum distance

minimum time

GCS Trajectory Optimization

Convex optimization problems as "Convex Sets"

  • For GcsTrajOpt, each convex set is a mathematical program
    • ​(convex) kinematic trajectory optimization
    • Bezier curves + time scaling

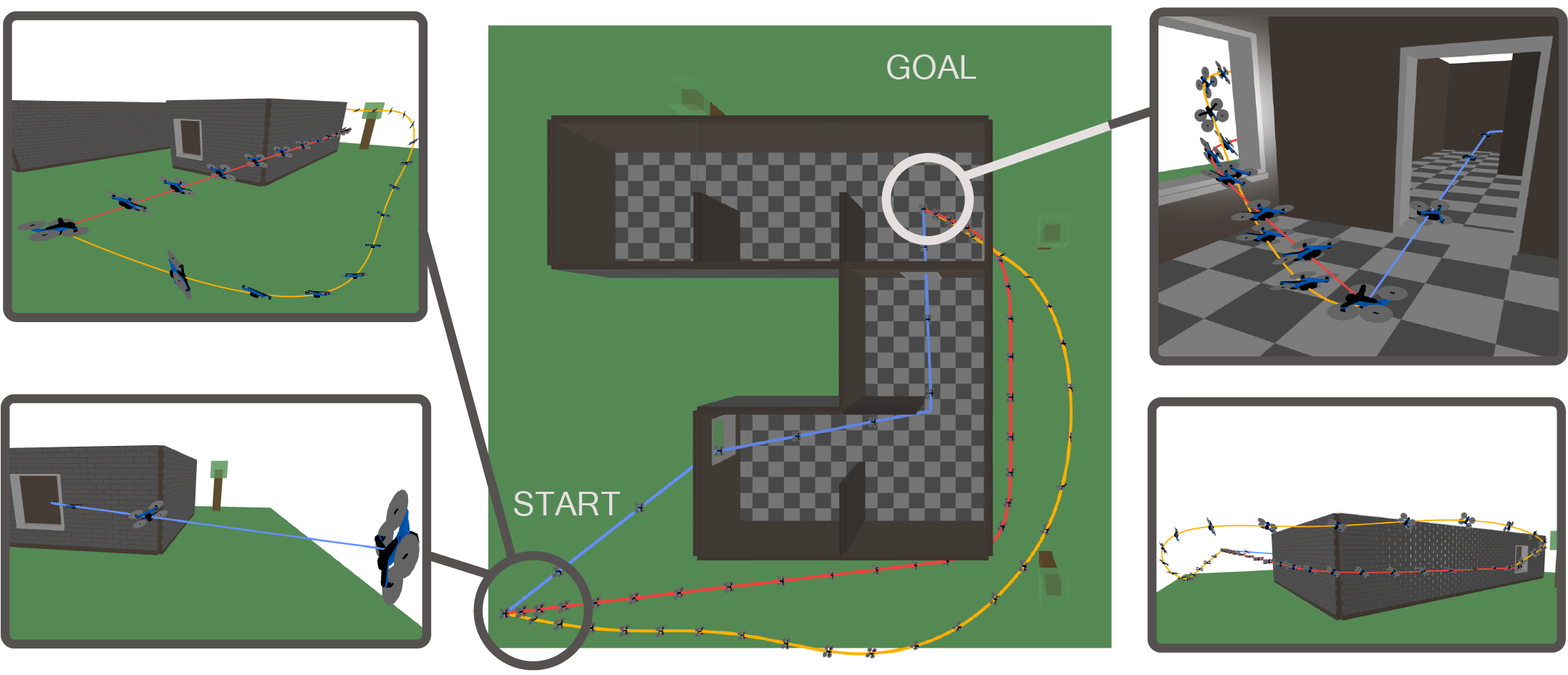
Discrete paths + continuous (convex via differential flatness)

GCS Trajectory Optimization

Transitioning from basic research to real use cases

Now Amazon is running with it... 

on its next-gen ASIN manipulation program

Back at MIT - focusing on the fundamentals

This morning we had talks by the students, including...

  • Custom solvers for GCS problems
    • GCS generates very sparse / structured optimization problems.
    • But the API to all commercial / open-source solvers destroys this sparsity, for example: 
      • Constraints of the form \(AxB=C\), with \(A, B,\) and \(C\) sparse.
      • Rewriting them as \(\bar{A}x=b\) destroys the sparsity
      • Generalize ADMM and interior point to deal take \(AxB=C\) directly

Back at MIT - focusing on the fundamentals

  • Convex decomposition of configuration space is still hard
    • presented several new decomposition algorithms
    • an entirely new convex relaxation that avoids decomposition entirely

Aside: This work uncovered a compelling geometric interpretation of the "standard" SDP relaxation; another math paper coming!

Real2Sim

2021

2025

Motion Planning

"Real2Sim"

Theory of Visuomotor Control

Long-time collaboration with Amazon using Drake

drake.mit.edu

SDE Interpretation

Positive Transfer: Power Laws

SDE Interpretation

Scalable Real2Sim

How can we scalably obtain simulation assets?

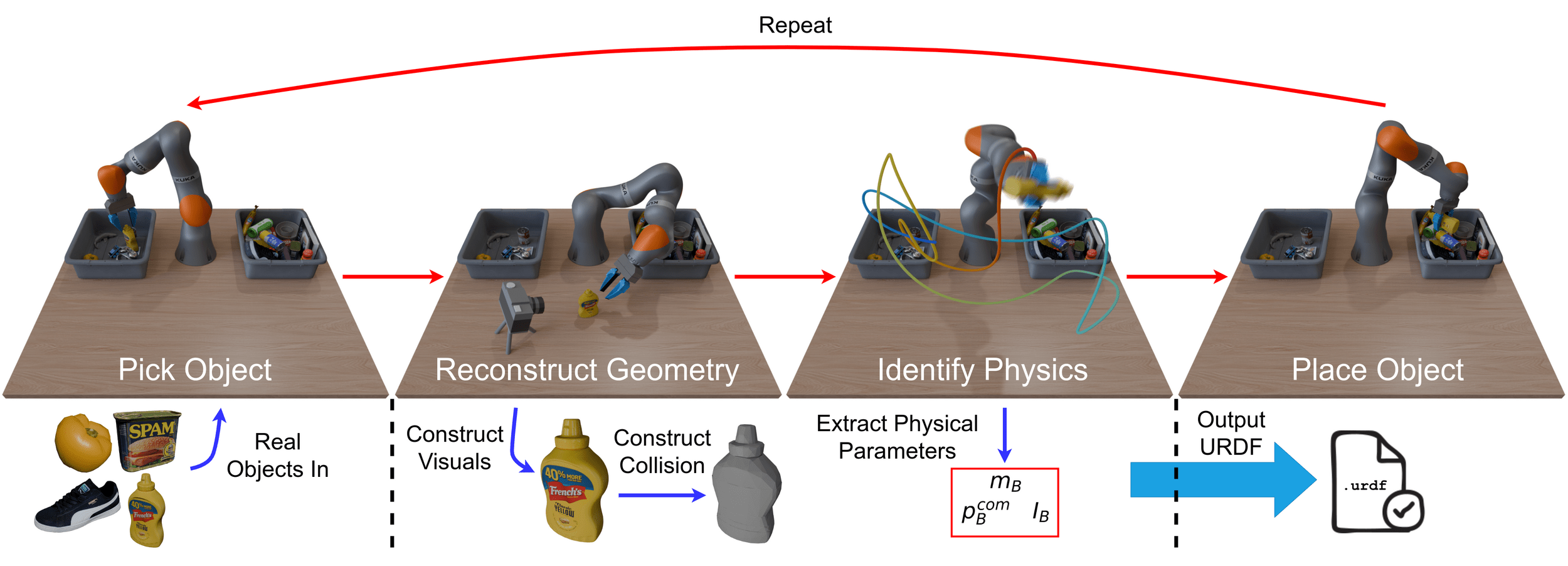
Estimating Inertial Parameters

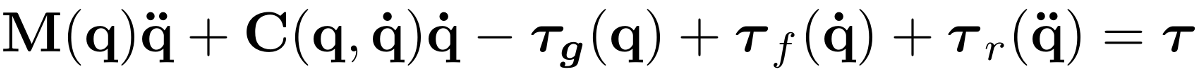
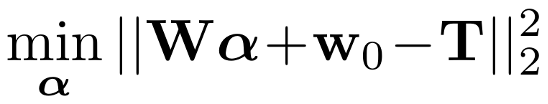
joint angles

joint torques

Data matrix:

s.t.

pseudo-inertia

+ optimal experiment trajectory design

SDE Interpretation

Positive Transfer: Power Laws

SDE Interpretation

Scalable Real2Sim

We've generated a significant object dataset.  Jeremy at Amazon is using it now and really scaling it up.

Steerable Scene Generation

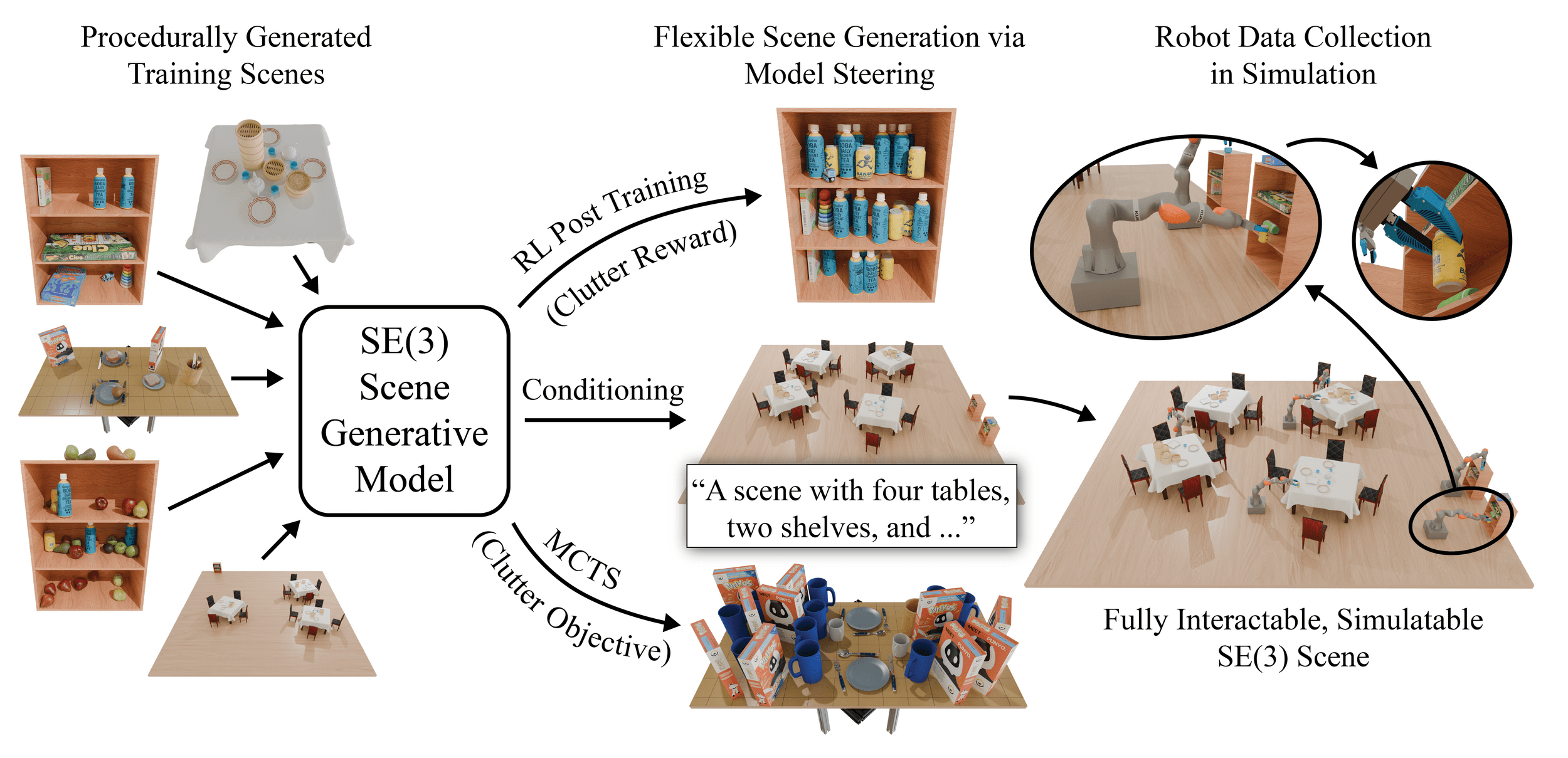
Steerable Scene Generation

Diffusion Policies &

Large Behavior Models

2021

2025

Motion Planning

"Real2Sim"

Theory of Visuomotor Control

Robotics: Science and Systems, 2023

International Journal of Robotics Research, 2024

Diffusion Policy (DP) is "single-task"

  • Train on ~200 demonstrations
  • \(\Rightarrow\) visuomotor policy

LBMs are "multitask"

  • Train on all robot data + internet data
  • \(\Rightarrow\) language-conditioned visuomotor policy

vision encoder

language encoder

action

decoder

robot joint encoder

vision encoder

action

decoder

robot joint encoder

LLMs \(\Rightarrow\) VLMs \(\Rightarrow\) LBMs

large language models

visually-conditioned language models

large behavior models

\(\sim\) VLA (vision-language-action)

\(\sim\) EFM (embodied foundation model)

vision encoder

language encoder

action

decoder

robot joint encoder

The opportunity

  • New levels of dexterity (manipulating cloth, liquids, etc)​​
  • Programmed via imprecise natural language and/or a few demonstrations
  • "Common-sense" for physical intelligence \(\Rightarrow\) open-world robustness
  • For Amazon: 
    • Foundation models for perception + planning and control can (and should) address big slices of the pie. 
    • Farther from the FCs \(\Rightarrow\) less structured.
    • Even in the FCs, LBMs can address the long tails.

The challenge

  • Empirical results raced far ahead of our theory.
  • Learned policies have real limits (e.g. short memory), and training is hugely inefficient.

We need to develop the new theory of (visuomotor) control.

Spotlight: Long-context policies

Diffusion Policy / Large Behavior Models from TRI have a context length of 2.

RT-1, RT-2, OpenVLA, \(\pi_0\), ... all have a context length of 1.

Why?

Even with more data, training with a longer context length makes performance worse.

Spotlight: Long-context policies

Idea #1: Study diffusion policy for Linear-Quadratic Gaussian control problems.

  • Derived basic sample-complexity bounds based on context length.
  • But it turns out long context lengths work fine for LQG.

Idea #2: Construct the simplest possible experiments that do exhibit the problem, and study them empirically. 

  • Found one problem with the vision encoders in simple UNet-style Diffusion.
  • Partial mitigation: train short context, freeze the image encoder, then train again.

Spotlight: Sim-and-Real Cotraining

\red{\mathcal{D}_{R}\sim p_{R}(O,A)}
\blue{\mathcal{D}_S\sim p_{S}(O,A)}

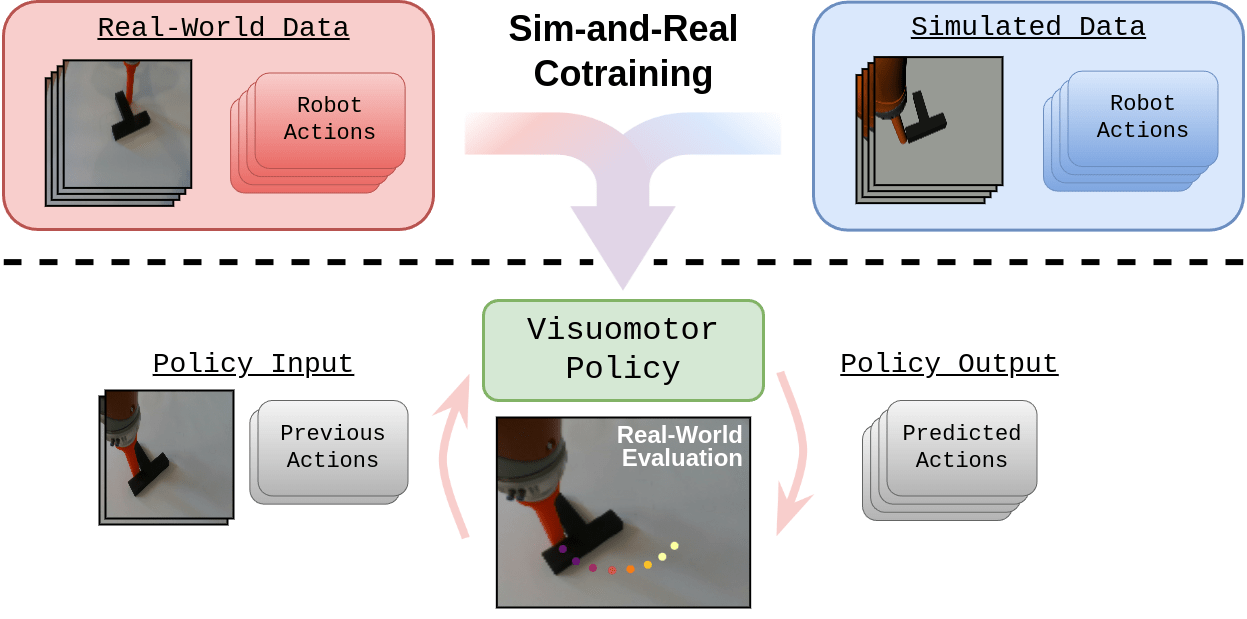
Cotraining: Use both datasets to train a model that maximizes some real-world performance objective

Notation:
\(\mathcal D\) - dataset
\(O\) - observations
\(A\) - actions
\(R\) - real
\(S\) - sim

Experimental Setup

Cotraining: Use both datasets to train a model that maximizes some real-world performance objective

Objective:

Success rate on planar pushing from pixels

Limited to single task, but carefully controlled experiments and thorough analysis​​

Experimental Setup

Cotraining: Use both datasets to train a model that maximizes some real-world performance objective

Datasets:

Model:

Diffusion Policy

\mathcal L_{\mathcal D^\alpha} = \alpha \textcolor{red}{\mathcal L_{\mathcal D_R}} + (1-\alpha) \textcolor{blue}{\mathcal L_{\mathcal D_S}}

[1] Graedsal et. al, "Towards Tight Convex Relaxations For Contact-Rich Manipulation"

Real Data, \(\mathcal D_R\)

Sim Data, \(\mathcal D_S\)

Objective:

Success rate on planar pushing from pixels

\(\mathcal L_{\mathcal D}\) - denoising loss for dataset \(\mathcal D\)
\(\alpha\) - mixing ratio

Scaling Sim Data

  • Performance gains from scaling sim data plateau; additional real data raises the performance ceiling
  • Sim data gen is valuable! But cannot fully replace real data

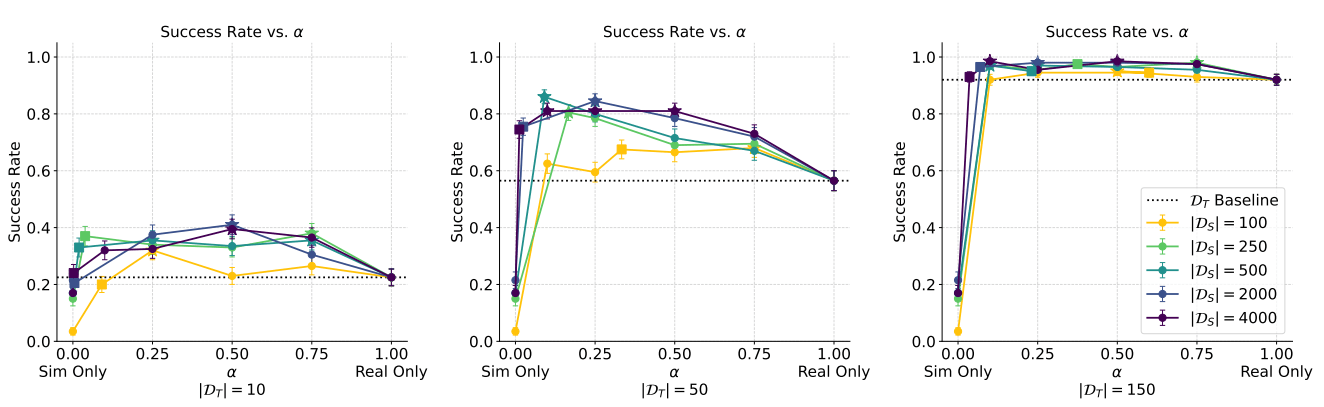
Distribution Shift Experiments

We investigate 6 sim2real gaps:

  • Visual shifts: color shift, color randomization, camera shift
  • Physical shifts: center of mass shift
  • Task shifts: goal shifts, object shifts

Key Findings

  • All shifts reduce performance; physics and task shift are most impactful
  • Paradoxically, some visual shift is required for good performance!

(for planar pushing...)

Spotlight: Post-training Diffusion Policy 

  • Step 1: Behavior Cloning
    • from human expert games
  • Step 2: Self-play
    • Policy network
    • Value network
    • Monte Carlo tree search (MCTS)

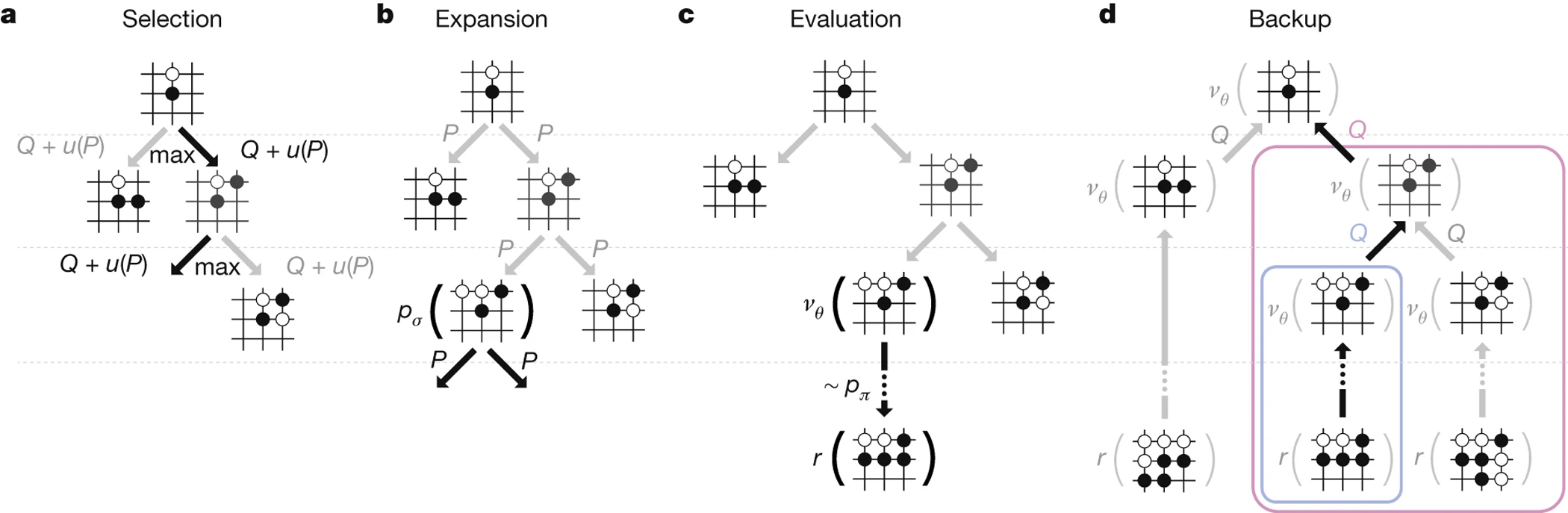
Learning and Planning

  • Two aspects of "intelligence"; either alone seems insufficient
  • Learning guides the planning (explore high-scoring actions)
  • Planning speeds up the learning
  • Planning immediately strengthens the policy -- potentially even when we move to "zero-shot" in "open world" domains.

Post-training for box unloading

Wrapping Up

One big request

On campus, we're feeling very limited with compute.

 

AWS credits via the Science Hub/research awards are ineffective with non-discounted AWS pricing.

 

It has become a real bottleneck.

Summary

  • Consistent, patient support from Amazon has enabled fundamental science and transfer all of the way to production at Amazon.
  • I presented three story arcs:
    • Motion planning (w/ Graphs of Convex Sets)
    • Real2Sim
    • the beginnings of a new Theory for Visuomotor Control


Thank you for the support!

drake.mit.edu

For a living doc with up-to-date references / examples:

https://underactuated.mit.edu/optimization.html#gcs