Shortest Paths in Graphs of Convex Sets

Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake. Shortest Paths in Graphs of Convex Sets. On arxiv.  Submitting to TAC (hopefully this week).

Shortest Paths on Graphs of Convex Sets

          is the convex relaxation.  (it's tight!)

Example: "Footstep planning" with \(x_{n+1}=Ax_n + Bu_n\)

Previous best formulations New formulation
Lower Bound
(from convex relaxation)		 7% of MICP 80% of MICP

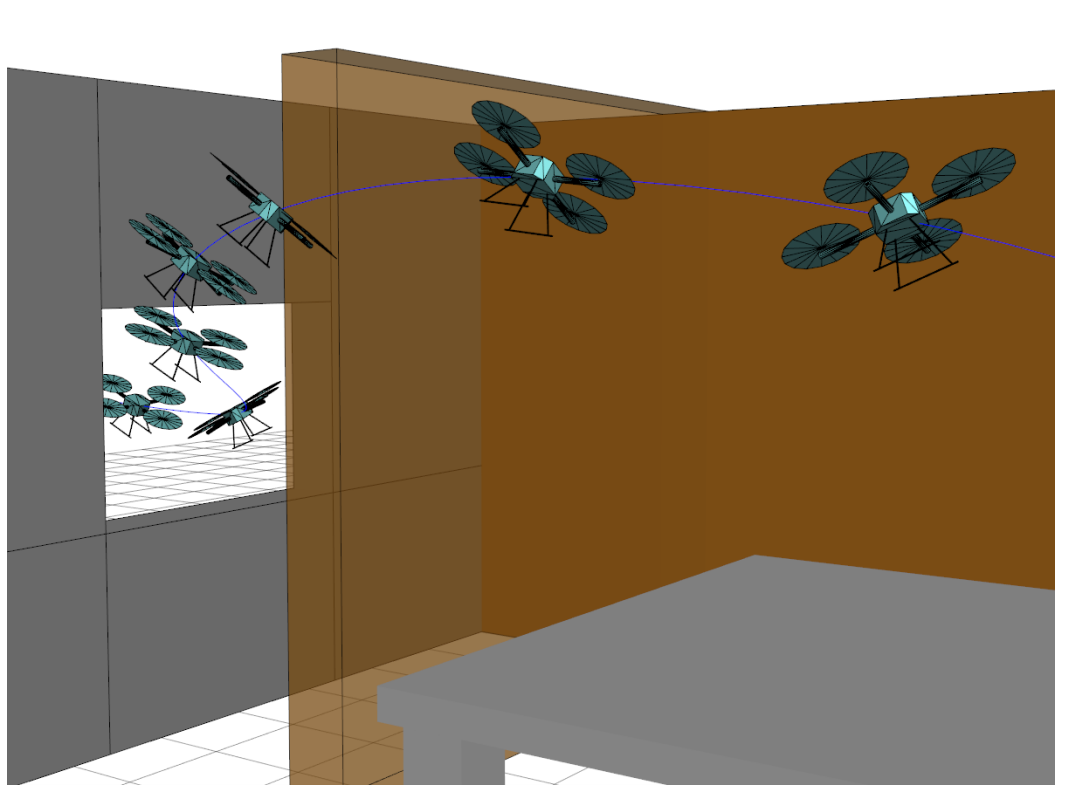
Collision-free planning with dynamic constraints

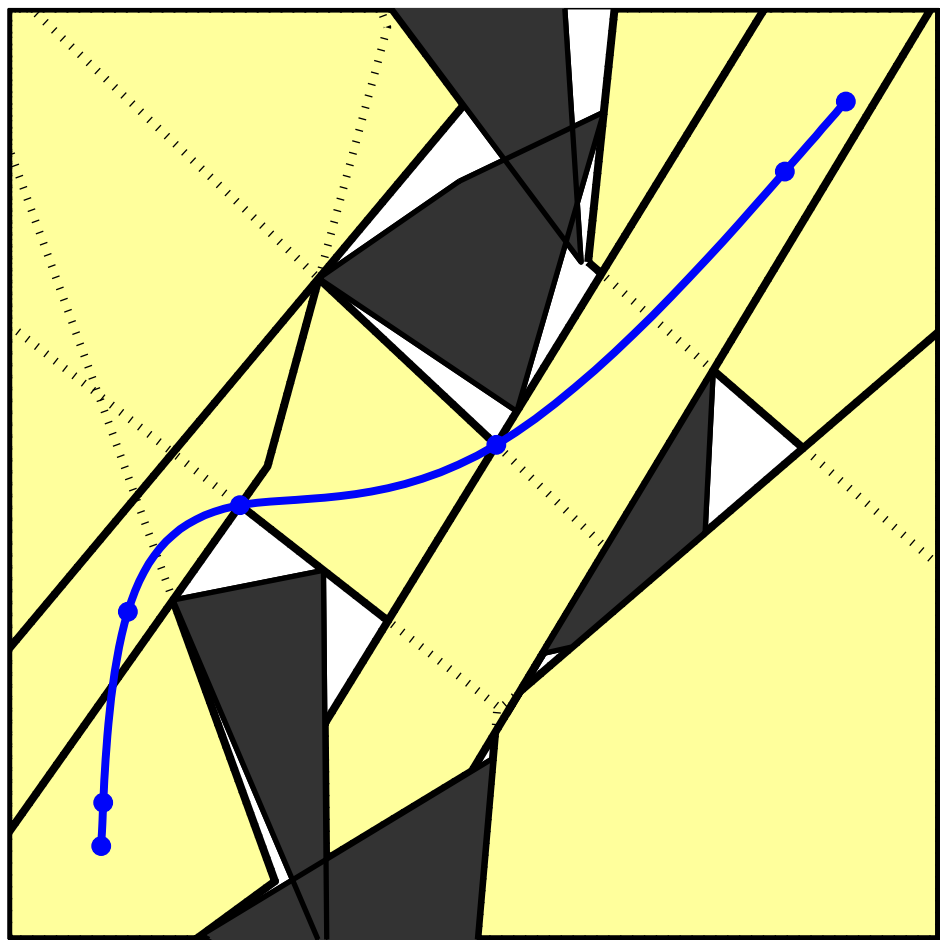
IRIS (Fast approximate convex segmentation)

  • Iteration between (large-scale) quadratic program and (relatively compact) semi-definite program (SDP)
  • Scales to high dimensions, millions of obstacles
  • ... enough to work on raw sensor data
  • Guaranteed collision-free along dynamic trajectories
  • Complete/globally optimal within convex decomposition

Non-smooth mechanics of contact

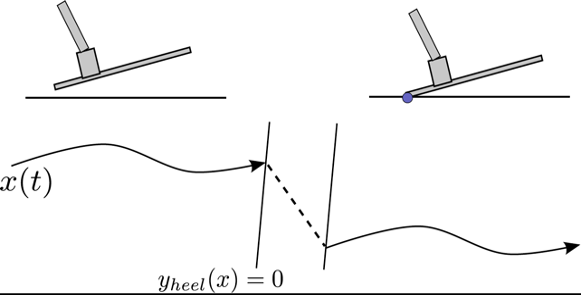
Contact forces are

  • discontinuous (or stiff) -- no force unless we have contact.
  • set-valued (e.g. Coulomb friction)

 

\( \Rightarrow \) Piecewise-affine or mixed logical-dynamical systems (MLDS)

  • Physics-based (time-stepping)
  • Deep models (e.g. w/ ReLU and max pooling)

Down to the essence

  • Vertices \(V\)
  • (Directed) edges \(E\)

 

  • For each \(i \in V:\)
    • Compact convex set \(X_i \subset \R^d\)
    • A point \(x_i \in X_i \) 

Down to the essence

  • Edge length given by a convex function \[ \ell(x_i, x_j) \]

  • Shortest path, \(P:\) \[ \min_P \min_{(x_i)_{i \in P}} \sum_{(i,j) \in P} \ell(x_i,x_j).\]

 

  • Can also add constraints on \(x_i, x_j\).

Traditional Shortest Path as a Linear Program (LP)

\(\varphi_{ij} = 1\) if the edge \((i,j)\) in shortest path, otherwise \(\varphi_{ij} = 0.\)

\(c_{ij} \) is the (constant) length of edge \((i,j).\)

\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\ \mathrm{s.t.} \quad & \sum_{j \in O_i} \varphi_{ij} - \sum_{j \in I_i} \varphi_{ji} = \delta_{si} - \delta_{ti}, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

New formulation

\begin{aligned} \min_{\varphi,x} \quad & \sum_{(i,j) \in E} \ell_{ij}(x_i, x_j) \varphi_{ij} \\ \mathrm{s.t.} \quad & x_i \in X_i, && \forall i \in V, \\ & \sum_{j \in O_i} \varphi_{ij} - \sum_{j \in I_i} \varphi_{ji} = \delta_{si} - \delta_{ti}, && \forall i \in V, \\ & \varphi_{ij} \geq 0, && \forall (i,j) \in E. \end{aligned}

Use convex hull reformulation + perspective functions to rewrite this as mixed-integer convex.

  • When sets \( X_i \) are points, reduces to standard LP formulation of the shortest path (known to be tight).

 

  • There are instances of this problem that are NP-hard.

 

  • Can strengthen convex relaxation by adding additional convex constraints (implied by binary feasibility).

 

  • Can add (piecewise-affine) dynamic constraints on pairs \( (x_i,x_j). \)

Remarks

Scaling

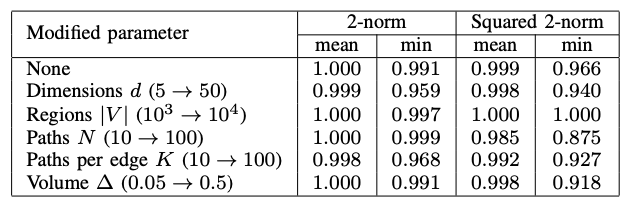
Euclidean shortest path

Finding the shortest path from A to B while avoiding polygonal obstacles (“Euclidean shortest path”):

  • Solvable in polytime in 2d (with a visibility graph)
  • NP-hard from 3 dimensions on
  • For the 3d case there exists an approximation algorithm which gives you eps-optimality in poly time
  • Nothing is known for \(d \ge 4\)

 

Our approach:

  • Provides polynomial-time algorithm for \(d \ge 4\) that is often tight.
  • Solves a more general class of problems (e.g. can add dynamic constraints).
  • WIP: Certificate of optimal solutions with high probability given a suitable rounding strategy.

Should be suitable for many graph-based optimization problems

Going forward...

Example: Bipartite matching (with convex regions)

Potential Implications for Manipulation

  • Could have implications for even traditional collision-free optimal motion planning?
  • Major advantage is supporting (piecewise-affine) dynamic constraints
  • Now exploring model-based planning through contact (physics models and perhaps deep models)
  • Recent results on Warm-starting mixed-integer MPC (Marcucci and Tedrake, 2020).

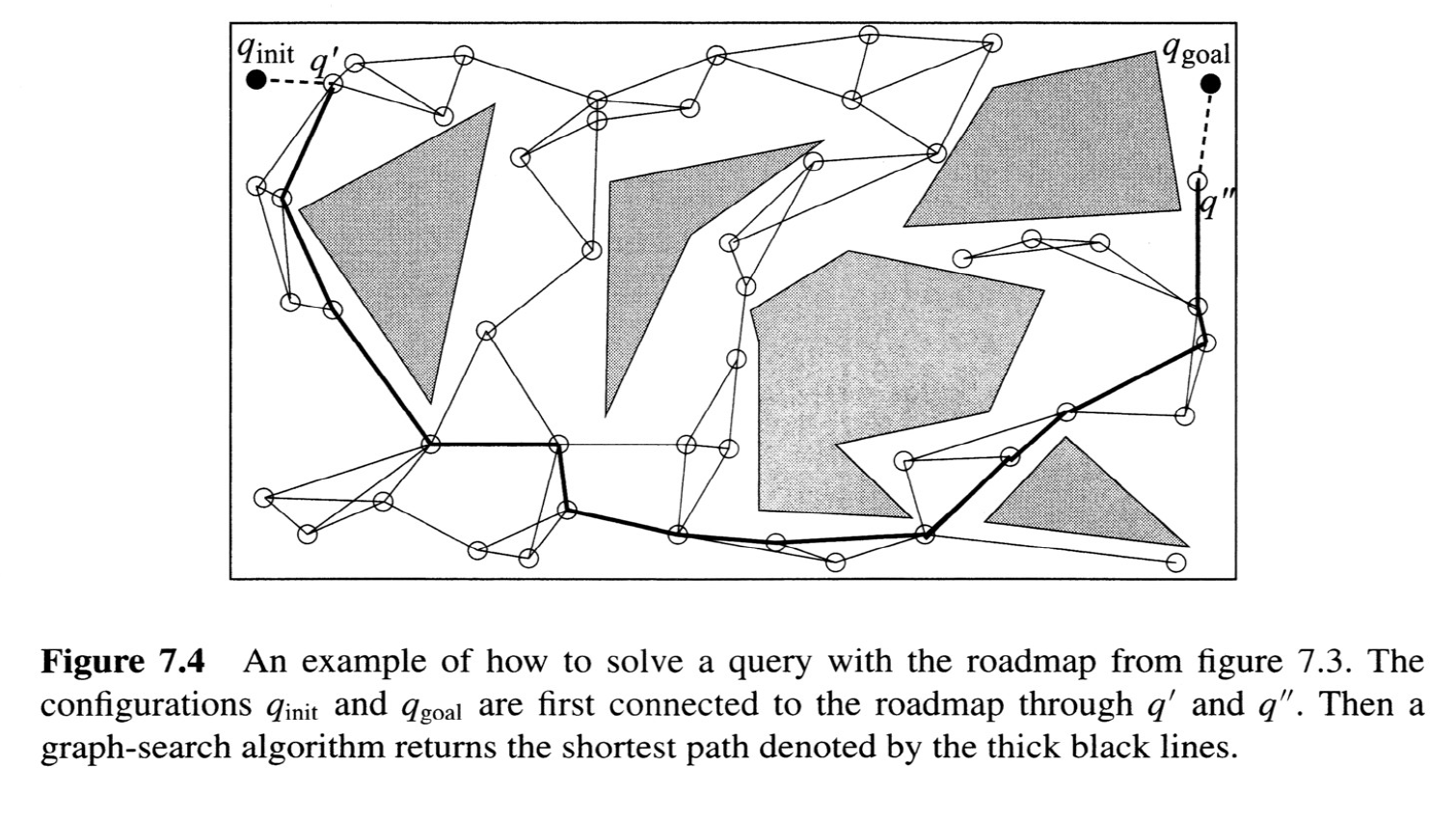
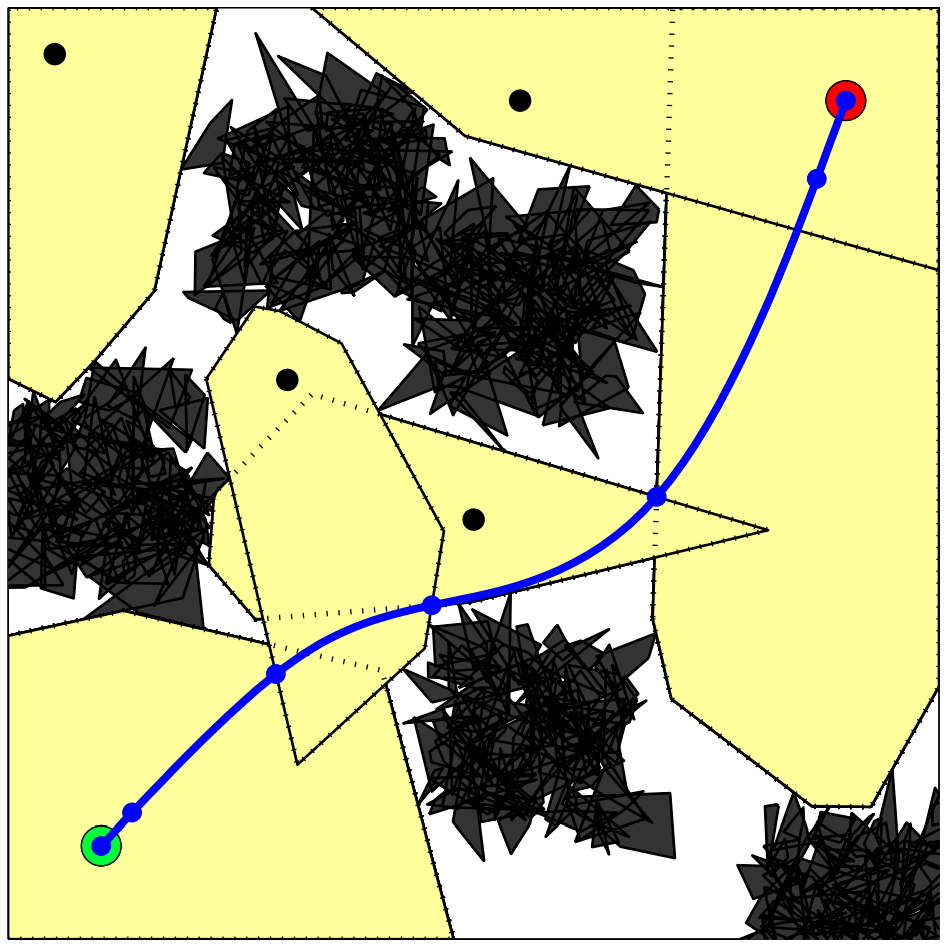
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.

Summary

  • New strong mixed-integer convex formulation for shortest path problems over convex regions
    • reduces to shortest path as regions become points
    • NP-hard; but strong formulation \(\Rightarrow\) efficient B&B
    • Convex relaxations are often tight!  \(\Rightarrow\) Rounding strategies
  • Should generalize to many graph optimizations / applications

Still need

  • better models/state representations
  • stronger planning/control design strategies.