Model-based RL / Intuitive Physics

MIT 6.800/6.843:

Robotic Manipulation

Fall 2021, Lecture 21

Follow live at https://slides.com/d/YPYIYRA/live

(or later at https://slides.com/russtedrake/fall21-lec21)

As more people started applying RL to robots, we saw a distinct shift from "model-free" RL to "model-based" RL.

   (most striking at the 2018 Conference on Robot Learning)

IFRR global panel on "data-driven vs physics-based models"

(caveat: I didn't choose the panel name)

What is a (dynamic) model?

System

..., u_{-1}, u_0, u_1, ...
..., y_{-1}, y_0, y_1, ...

State-space

Auto-regressive (eg. ARMAX)

input

output

p(\theta, x_0, w_0, w_1, ...)
x_{n+1} = f(n, x_n, u_n, w_n, \theta) \\ \quad y_n = g(n, x_n, u_n, w_n, \theta)
y_{n+1} = f(n, u_n, u_{n-1}, ..., \\ \qquad \qquad y_n, y_{n-1}, ..., \\ \qquad \qquad w_n, w_{n-1}, ..., \theta)

state

noise/disturbances

parameters

Lagrangian mechanics,

Recurrent neural networks (e.g. LSTM), ...

Feed-forward networks

(e.g. \(y_n\)= image)

What is a (dynamic) model?

System

..., u_{-1}, u_0, u_1, ...
..., y_{-1}, y_0, y_1, ...

State-space

Auto-regressive (eg. ARMAX)

input

output

x_{n+1} = f(n, x_n, u_n, w_n, \theta) \\ \quad y_n = g(n, x_n, u_n, w_n, \theta)
y_{n+1} = f(n, u_n, u_{n-1}, ..., \\ \qquad \qquad y_n, y_{n-1}, ..., \\ \qquad \qquad w_n, w_{n-1}, ..., \theta)

Models come in many forms

..., u_{-1}, u_0, u_1, ...
..., y_{-1}, y_0, y_1, ...

input

cost-to-go

Q-functions are models, too.  They try to predict only one output (the cost-to-go).

 

As you know, people are using Q-functions in practice on non-Markovian state representations.

\[ Q^{\pi}(n, x_n,u_n, \theta) \]

Model "class" vs model "instance"

  • \(f\) and \(g\) describe the model class.
  • with \(\theta\) describes a model instance.

 

"Deep models vs Physics-based models?" is about model class:

Should we prefer writing \(f\) and \(g\) using physics or deep networks?

Maybe not so different from

  • should we use ReLU or \(\tanh\)?
  • should we use LSTMs or Transformers?
x_{n+1} = f(n, x_n, u_n, w_n, \theta) \\ \quad y_n = g(n, x_n, u_n, w_n, \theta)

Galileo, Kepler, Newton, Hooke, Coulomb, ...

were data scientists.

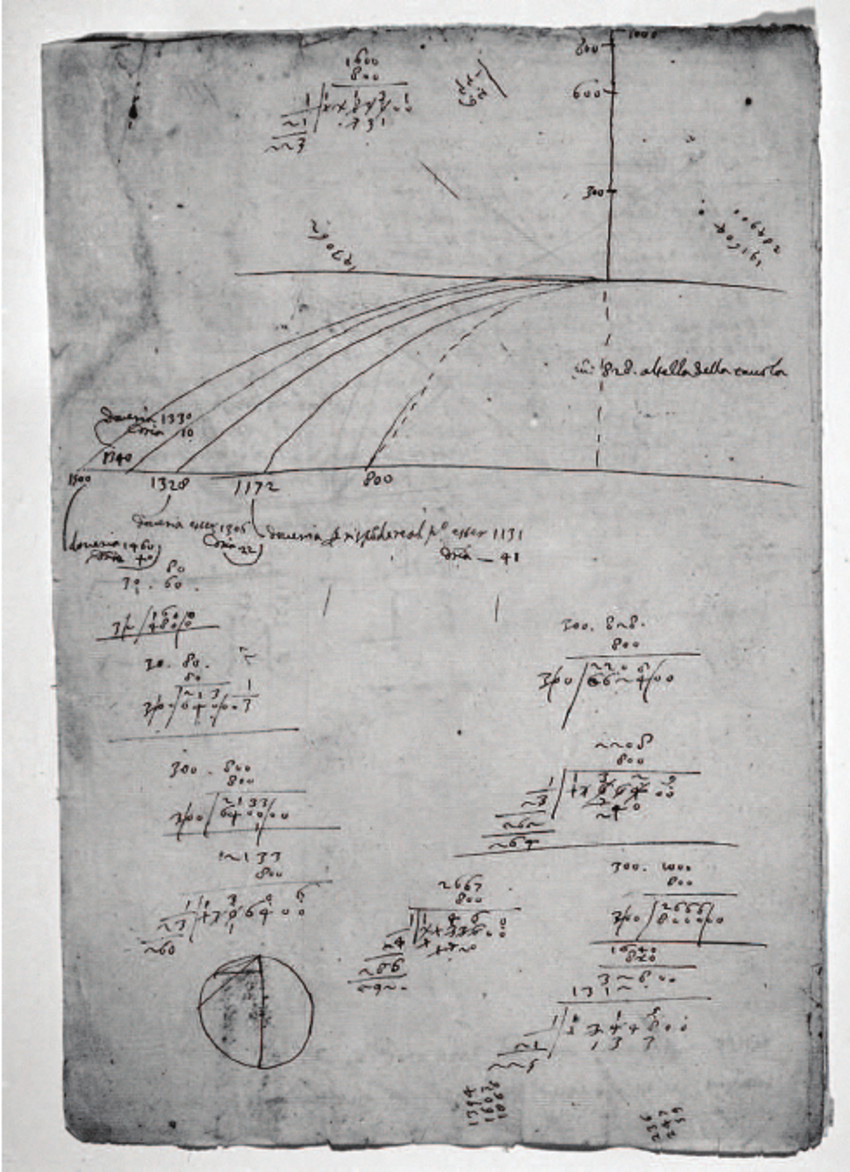
They fit very simple models to very noisy data.

Gave us a rich class of parametric models that we could fit to new data.

What if Newton had deep learning...?

Galileo's notes on projectile motion

What makes a model class useful?

"All models are wrong, but some are useful" -- George Box

Use case: Simulation

e.g., for

  • generating synthetic training data
  • Monte-Carlo policy evaluation
  • offline policy optimization

 

What makes a model class useful?

  • Reasonable: \( y_{sim}(u) \in \{ y_{real}(u) \} \)
  • Coverage: \( \forall y_{real}(u), \exists y_{sim}(u) \)
  • Accuracy: \( p(y_{real} | u) \approx p(y_{sim} | u) \)
  • Corollary:  Reliable system identification (data \( \Rightarrow \theta \))
  • Generalizable, efficient, repeatable, interpretable/debuggable, ... 

Unreal 5 engine trailer

Use case: Online Decision Making (Planning/Control)

What makes a model class useful?

  • Reasonable, Accurate, Generalizable, ...
  • Efficient / compact
  • Observable
  • Task-relevant

State-space models tend to be more efficient/compact, but require state estimation.

  • Ex: chopping onions.
    • Lagrangian state not observable.
    • Task relevant?
  • Doesn't imply "no mechanics"
x_{n+1} = f(n, x_n, u_n, w_n, \theta) \\ \quad y_n = g(n, x_n, u_n, w_n, \theta)
y_{n+1} = f(n, u_n, u_{n-1}, ..., \\ \qquad \qquad y_n, y_{n-1}, ..., \\ \qquad \qquad w_n, w_{n-1}, ..., \theta)

vs.

Auto-regressive

State-space

Occam's razor and predicting what won't happen

Perhaps the biggest philosophical difference between traditional physics models and "universal approximators".

  • \( f,g\) are not arbitrary.  Mechanics gives us constraints:
    • Conservation of mass
    • Conservation of energy
    • Maximum dissipation
    • ...
  • Arguably these constraints give our models their structure
    • Control affine
    • Inertial matrix is positive definite
    • Inverse dynamics have "branch-induced sparsity"
  • Without structure, maybe we can only ever do stochastic gradient descent...?

The failings of our physics-based models are mostly due to the unreasonable burden of estimating the "Lagrangian state" and parameters.

For e.g. onions, laundry, peanut butter, ...

The failings of our deep models are mostly due to our inability to due efficient/reliable planning, control design and analysis, to make sufficiently accurate long-horizon predictions, and to generalize under distribution shift.

I want the next Newton to come around and to work on onions, laundry, peanut butter...

American Controls Conference (ACC), 1991

Dense Object Nets for Model-Predictive Control (MPC)

Learn descriptor keypoint dynamics + trajectory MPC

Learn descriptor keypoint dynamics + trajectory MPC

Some take-aways:

  • Can train a network to predict keypoint dynamics even for complex tasks ("hat on rack").
  • But planning/control is still hard.

Lucas at his defense: "Perception doesn't feel like the bottleneck anymore; it fees like the bottleneck is control."

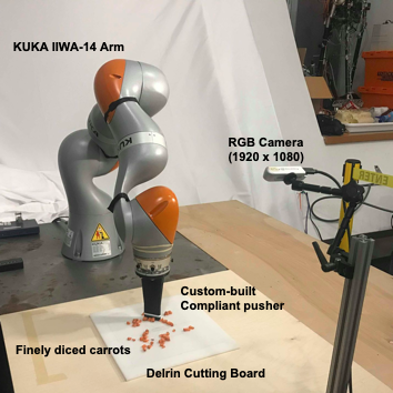
The Onion Problem

H.J. Terry Suh and Russ Tedrake. The surprising effectiveness of linear models for visual foresight in object pile manipulation. To appear in Workshop on the Algorithmic Foundations of Robotics (WAFR), 2020

The Onion Problem

Target Set

Carrot

 

The big question:

When is feedback "from pixels to torques" easy?

Problem Statement

Find a single policy (pixels to torques) that is invariant to the number of carrot pieces.

 

  • Objective: Move all carrot pieces to a “target set” on the cutting board.
  • Inputs (actions):  Discrete push, parameterized from (x1, y1) to (x2, y2)
  • Outputs (observations):  Images, I[n], or vectorized images y[n]

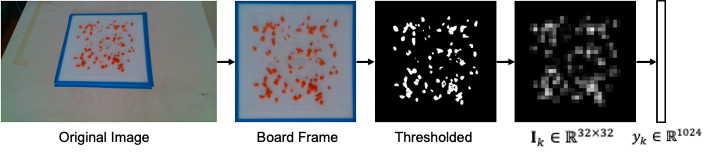
Try images as the state representation.

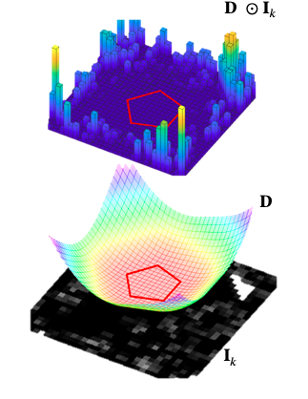
A control-Lyapunov function in image coordinates

Requires a forward model...

Crazy:  Try a linear model (for each discretized action)

A^* = \argmin_{A} \| Y_{k+1} - AY_k \|_F \\ \text{subject to} \quad A_{ij} \ge 0
Y_{k+1}
Y_{k}
A
=

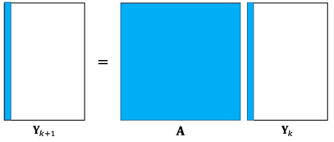
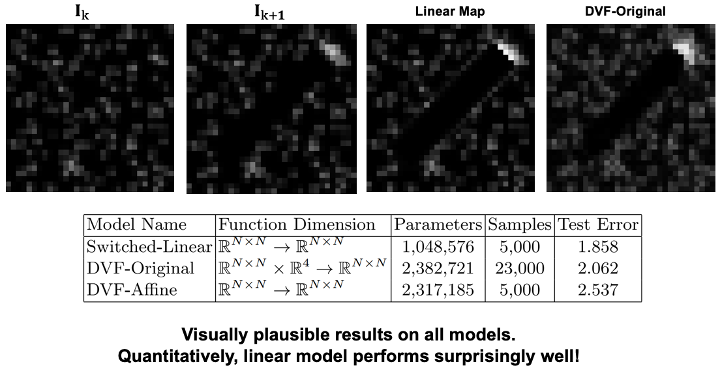
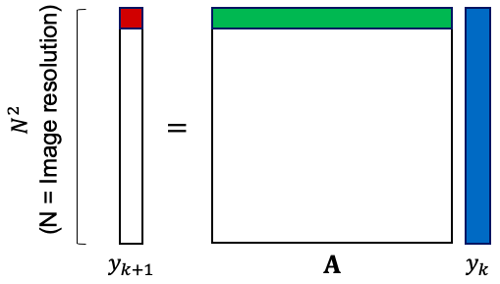
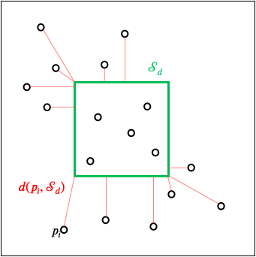
Each row of     is an image, the "receptive field" of

A
y_{k+1}

My take-aways:

 

  • Not saying that linear models are better than deep.
    • In fact: Yunzhu Li has now done better with a CNN.
  • This won't work for most problems.

 

  • When is pixels-to-torques easy?
    • One answer: When each pixel moves independently
    • Image acts like a probability density, dynamics as a transition matrix.

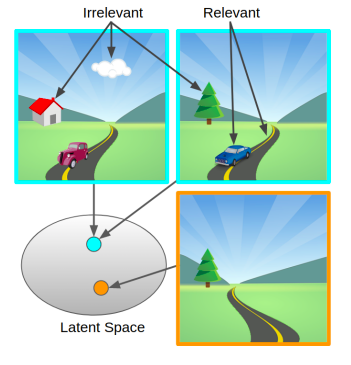
LEARNING INVARIANT REPRESENTATIONS FOR REINFORCEMENT LEARNING WITHOUT RECONSTRUCTION

Amy Zhang, Rowan McAllister, Roberto Calandra, Yarin Gal, Sergey Levine

ICLR 2021

from "Draping an Elephant: Uncovering Children's Reasoning About Cloth-Covered Objects" by Tomer Ullman et al, 2019